icoding题解排序
数组合并
假设有 n 个长度为 k 的已排好序(升序)的数组,请设计数据结构和算法,将这 n 个数组合并到一个数组,且各元素按升序排列。即实现函数:
void merge_arrays(const int* arr, int n, int k, int* output);
其中 arr 为按行优先保存的 n 个长度都为 k 的数组,output 为合并后的按升序排列的数组,大小为 n×k。
时间要求(评分规则),当 n > k 时:
- 满分:时间复杂度不超过 O(n×k×log(n))
- 75分:时间复杂度不超过 O(n×k×log(n)×k)
- 59分:其它,如:时间复杂度为 O(n2×k2) 时。
#include<stdio.h>
#include<stdlib.h>void max_heapify(int* p, int i, int size) {int j = 2 * i + 1, t=p[i];while (j <= size - 1) {if (j + 1 <= size - 1 && p[j] < p[j + 1])j = j + 1;if (p[j] > t) {p[i] = p[j];i = j;j = 2 * i + 1;}else break;}p[i] = t;
}//假设i之后都是大根堆,调整i使从i开始都是大根堆void merge_arrays(const int* arr, int n,int k,int* output) {int size=n*k;int x, i, *array;array = (int*)malloc(size * sizeof(int));for (i = 0; i <= size - 1; i++) {array[i] = arr[i];}for (i=size/2-1; i >=0 ; i--) {max_heapify(array, i, size);}//将整个堆大根堆化for (i = size-1; i >= 1; --i) {x = array[0];array[0] = array[i];array[i] = x;max_heapify(array, 0, i);}for (i = 0; i <= size - 1; i++) {output[i] = array[i];}}
堆化
二叉堆一般用数组来表示。例如,根节点在数组中的位置是0,第n个位置的子节点分别在2n+1和 2n+2。 因此,第0个位置的子节点在1和2,1的子节点在3和4。以此类推。这种存储方式便于寻找父节点和子节点。在二叉堆上可以进行插入节点、删除节点、取出值最小的节点、减小节点的值等基本操作。
“最小堆”的定义如下:
typedef struct _otherInfo
{int i;int j;
}OtherInfo;typedef struct _minHeapNode
{int value;OtherInfo otherInfo;
}MinHeapNode, *PMinHeapNode;typedef struct _minPQ {PMinHeapNode heap_array; // 指向堆元素数组int heap_size; // 当前堆中的元素个数int capacity; //堆数组的大小
}MinHeap, *PMinHeap;
请实现最小堆的“堆化”函数:
void min_heapify(PMinHeap pq, int i);
其中 pq指向堆,i 为堆元素在数组中的下标。该函数假设元素i对应的子树都已经是最小堆(符合最小堆的要求),但元素i为根的子树并不是最小堆,min_heapify将对元素i及其子树的各结点进行调整,使其为一个最小堆。
(注:假设辅助函数 left、right、parent 和 swap_node 已正确实现,min_heapify 函数可直接使用。)
#include <stdio.h>
#include <stdlib.h>
#include "minbinheap.h"void min_heapify(PMinHeap pq, int i){int j = 2 * i + 1;MinHeapNode* p = pq->heap_array;while (j <= pq->heap_size - 1){//j为最小值的堆if (p[j + 1].value < p[j].value)j = j + 1;if (p[j].value < p[i].value) {swap_node(&p[j], &p[i]);i = j;j = 2 * i + 1;}else return;}
}堆元素插入
二叉堆一般用数组来表示。例如,根节点在数组中的位置是0,第n个位置的子节点分别在2n+1和 2n+2。 因此,第0个位置的子节点在1和2,1的子节点在3和4。以此类推。这种存储方式便于寻找父节点和子节点。在二叉堆上可以进行插入节点、删除节点、取出值最小的节点、减小节点的值等基本操作。
“最小堆”的定义如下:
typedef struct _otherInfo
{int i;int j;
}OtherInfo;typedef struct _minHeapNode
{int value;OtherInfo otherInfo;
}MinHeapNode, *PMinHeapNode;typedef struct _minPQ {PMinHeapNode heap_array; // 指向堆元素数组int heap_size; // 当前堆中的元素个数int capacity; //堆数组的大小
}MinHeap, *PMinHeap;
请实现最小堆的元素插入函数:
bool heap_insert_value(PMinHeap pq, int value);
其中 pq指向堆,value 为要插入的堆元素。
(注:假设辅助函数 parent 和 swap_node 已正确实现,heap_insert_value 函数可直接使用。)
#include <stdio.h>
#include <stdlib.h>
#include "minbinheap.h"
#define H pq->heap_arraybool heap_insert_value(PMinHeap pq, int value){if(pq->heap_size==pq->capacity)return false;int i=pq->heap_size;H[i].value=value;while(i!=0&&H[i].value<H[parent(i)].value){swap_node(&H[i],&H[parent(i)]);i=parent(i);}pq->heap_size++;return true;
}堆初始化
二叉堆一般用数组来表示。例如,根节点在数组中的位置是0,第n个位置的子节点分别在2n+1和 2n+2。 因此,第0个位置的子节点在1和2,1的子节点在3和4。以此类推。这种存储方式便于寻找父节点和子节点。在二叉堆上可以进行插入节点、删除节点、取出值最小的节点、减小节点的值等基本操作。
“最小堆”的定义如下:
typedef struct _otherInfo
{int i;int j;
}OtherInfo;typedef struct _minHeapNode
{int value;OtherInfo otherInfo;
}MinHeapNode, *PMinHeapNode;typedef struct _minPQ {PMinHeapNode heap_array; // 指向堆元素数组int heap_size; // 当前堆中的元素个数int capacity; //堆数组的大小
}MinHeap, *PMinHeap;
请实现最小堆的初始化函数:
void init_min_heap(PMinHeap pq, int capacity);
其中 pq指向堆,capacity为堆元素数组的初始化大小。
#include <stdio.h>
#include <stdlib.h>
#include "minbinheap.h"//pq指向堆,capacity为堆元素数组的初始化大小
void init_min_heap(PMinHeap pq, int capacity){pq->capacity = capacity;pq->heap_size = 0;pq->heap_array = (PMinHeapNode)malloc(sizeof(MinHeapNode) * pq->capacity);return;
}堆辅助函数
二叉堆是完全二叉树或者是近似完全二叉树。二叉堆有两种:最大堆和最小堆。
- 最大堆(大顶堆):父结点的键值总是大于或等于任何一个子节点的键值,即最大的元素在顶端;
- 最小堆(小顶堆):父结点的键值总是小于或等于任何一个子节点的键值,即最小的元素在顶端。
- 二叉堆子结点的大小与其左右位置无关。
二叉堆一般用数组来表示。例如,根节点在数组中的位置是0,第n个位置的子节点分别在2n+1和 2n+2。 因此,第0个位置的子节点在1和2,1的子节点在3和4。以此类推。这种存储方式便于寻找父节点和子节点。在二叉堆上可以进行插入节点、删除节点、取出值最小的节点、减小节点的值等基本操作。
“最小堆”的定义如下:
typedef struct _otherInfo
{int i;int j;
}OtherInfo;typedef struct _minHeapNode
{int value;OtherInfo otherInfo;
}MinHeapNode, *PMinHeapNode;typedef struct _minPQ {PMinHeapNode heap_array; // 指向堆元素数组int heap_size; // 当前堆中的元素个数int capacity; //堆数组的大小
}MinHeap, *PMinHeap;
请实现最小堆的四个辅助函数:
int parent(int i); //返回堆元素数组下标为 i 的结点的父结点下标
int left(int i); //返回堆元素数组下标为 i 的结点的左子结点下标
int right(int i); //返回堆元素数组下标为 i 的结点的右子结点下标
void swap_node(MinHeapNode *x, MinHeapNode *y); //交换两个堆元素的值#include <stdio.h>
#include <stdlib.h>
#include "minbinheap.h" // 请不要删除,否则检查不通过
int parent(int i) {
return (i-1) / 2;
}
int left(int i){
return 2 * i + 1;
}
int right(int j) {
return 2 * j + 2;
}
void swap_node(MinHeapNode* x, MinHeapNode* y) {
int value;
int i, j;
value = y->value;
i = y->otherInfo.i;
j = y->otherInfo.j;
y->value = x->value;
y->otherInfo.i = x->otherInfo.i;
y->otherInfo.j = x->otherInfo.j;
x->value = value;
x->otherInfo.i = i;
x->otherInfo.j = j;}
相关文章:

icoding题解排序
数组合并 假设有 n 个长度为 k 的已排好序(升序)的数组,请设计数据结构和算法,将这 n 个数组合并到一个数组,且各元素按升序排列。即实现函数: void merge_arrays(const int* arr, int n, int k, int* out…...
)
LangChain-检索系统 (Retrieval)
检索系统 (Retrieval) 检索系统是LangChain的核心组件之一,它提供了从各种数据源获取相关信息的能力,是构建知识增强型应用的基础。本文档详细介绍LangChain检索系统的组件、工作原理和最佳实践。 概述 检索系统解决了大型语言模型知识有限和过时的问…...

Fast网络速度测试工具
目录 网站简介 功能特点 测试过程 为什么使用Fast 如果网络速度不达标 网站简介 Fast是一个由Netflix提供的网络速度测试工具,主要用来测试用户的互联网下载速度。它以其简洁的界面和快速的测试过程而受到用户的欢迎。 功能特点 下载速度测试:这是…...
ubuntu20.04在mid360部署direct_lidar_odometry(DLO)
editor:1034Robotics-yy time:2025.4.10 1.下载DLO,mid360需要的一些...: 1.1 在工作空间/src下 下载DLO: git clone https://github.com/vectr-ucla/direct_lidar_odometry 1.2 在工作空间/src下 下载livox_ros_driver2&…...

制造企业数据治理体系搭建与业务赋能实践
当下制造企业正面临着前所未有的机遇与挑战,从多环节业务协同的复杂性,到海量数据资源的沉睡与孤岛化;从个性化定制需求的爆发,到供应链效率优化的迫切性——如何通过数据治理将“数据包袱”转化为“数据资产”,已成为…...

java基础多态------面试八股文
是什么是多态 类引用指向子类对象,并调用子类重写的方法,实现不同的行为 例子 class Animal {void sound() {System.out.println("动物发出声音");} }class Dog extends Animal {Overridevoid sound() {System.out.println("狗叫&…...

【LunarVim】解决which-key 自定义键位注册不成功问题
问题描述 LunarVim将which-key设置放在一个keymaps.lua中,然后config.lua调用reload “user.keymaps”,键位没用注册成功,而直接写在config.lua中,就注册成功 这暴露了LunarVim 插件和配置加载顺序的一些细节坑,下面解…...

开源推荐#5:CloudFlare-ImgBed — 基于 CloudFlare Pages 的开源免费文件托管解决方案
大家好,我是 jonssonyan。 寻找一个稳定、快速、还最好是免费或成本极低的图床服务,一直是许多开发者、博主和内容创作者的痛点。公共图床可能说关就关,付费服务又增加成本。现在,一个名为 CloudFlare-ImgBed 的开源项目…...

算法训练之动态规划(三)
♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥ ♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥ ♥♥♥我们一起努力成为更好的自己~♥♥♥ ♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥ ♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥ ✨✨✨✨✨✨ 个…...

xv6-labs-2024 lab2
lab-2 0. 前置 课程记录 操作系统的隔离性,举例说明就是,当我们的shell,或者qq挂掉了,我们不希望因为他,去影响其他的进程,所以在不同的应用程序之间,需要有隔离性,并且࿰…...
)
LangChain-模型输入输出 (Model I/O)
模型输入输出是LangChain的核心组件,负责处理与各种语言模型的交互。本文档详细介绍了这些组件的功能和使用方法。 概述 模型输入输出组件负责: 连接各种语言模型:统一不同提供商的模型接口格式化输入:将原始输入转换为模型可理…...

基于FPGA实现BPSK 调制
目录 一、 任务介绍二、基本原理三、基于FPGA实现BPSK 调制四、源码 一、 任务介绍 BPSK 调制在数字通信系统中是一种极重要的调制方式,它的抗干扰噪声性能及通频带的利用率均优先于 ASK 移幅键控和 FSK 移频键控。因此,PSK 技术在中、高速数据传输中得…...

深入理解 ResponseBodyAdvice 及其应用
ResponseBodyAdvice 是 Spring MVC 提供的一个强大接口,允许你在响应体被写入 HTTP 响应之前对其进行全局处理。 下面我将全面介绍它的工作原理、使用场景和最佳实践。 基本概念 接口定义 public interface ResponseBodyAdvice<T> {boolean supports(Metho…...
)
Java 基础 - 反射(1)
文章目录 引入类加载过程1. 通过 new 创建对象2. 通过反射创建对象2.1 触发加载但不初始化2.2 按需触发初始化2.3 选择性初始化控制 核心用法示例1. 通过无参构造函数创建实例对象2. 通过有参构造函数创建实例对象3. 反射通过私有构造函数创建对象, 破坏单例模式4. …...

Spring Boot中Spring MVC相关配置的详细描述及表格总结
以下是Spring Boot中Spring MVC相关配置的详细描述及表格总结: Spring MVC 配置项详解 1. 异步请求配置 spring.mvc.async.request-timeout 描述:设置异步请求的超时时间(单位:毫秒)。默认值:未设置&…...

flink Shuffle的总结
关于 ** 5 种 Shuffle 类型** 的区别、使用场景及 Flink 版本支持的总结: * 注意:下面是问AI具体细节与整理学习 1. 核心区别 Shuffle 类型核心特点使用场景Flink 版本支持Pipelined Shuffle流式调度,纯内存交换,低延迟(毫秒级…...

在排序数组中查找元素的第一个和最后一个位置 --- 二分查找
目录 一:题目 二:算法原理分析 三:代码实现 一:题目 题目链接: 34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode) 二:算法原理分析 三:代码实现 c…...
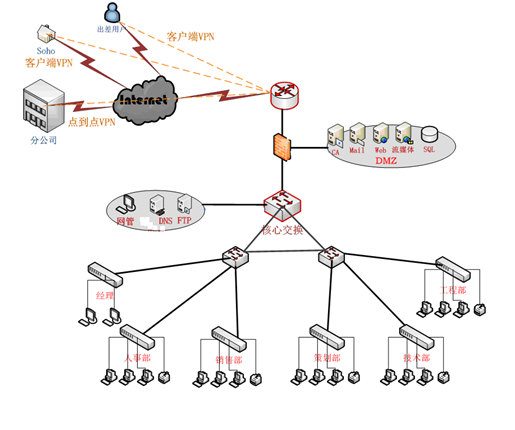
631SJBH中小型企业的网络管理模式的方案设计
1.1、研究现状 我国很多企业信息化水平一直还处在非常初级的阶段,有关统计表明,真正实现了计算机较高应用的企业在全国1000多万中小企业中所占的比例还不足10%幢3。大多数企业还停留在利用互联网进行网上查询(72.9%)、…...
)
NO.85十六届蓝桥杯备战|动态规划-经典线性DP|最长上升子序列|合唱队形|最长公共子序列|编辑距离(C++)
经典线性dp问题有两个:最⻓上升⼦序列(简称:LIS)以及最⻓公共⼦序列(简称:LCS),这两道题⽬的很多⽅⾯都是可以作为经验,运⽤到别的题⽬中。⽐如:解题思路&…...

0410 | 软考高项笔记:项目管理概述
以下是不同组织结构中项目经理的角色、工作特点以及快速记忆的方法: 不同组织结构中项目经理的角色和工作特点 组织结构项目经理的角色工作特点职能型组织项目协调者、辅助管理者权力有限,主要负责协调部门间的工作,项目成员向部门经理汇报…...

Vue3的Composition API与React Hooks有什么异同?
Vue3的一个重大更新点就是支持Composition API,而且也被业界称为hooks,那么Vue3的“Hooks”与React的Hooks有这么区别呢? 一、核心相似点 1. 逻辑复用与代码组织 都解决了传统类组件或选项式 API 中逻辑分散的问题,允许将相关逻…...

LangChain4j(1):初步认识Java 集成 LLM 的技术架构
LangChain 作为构建具备 LLM 能力应用的框架,虽在 Python 领域大放异彩,但 Java 开发者却只能望洋兴叹。LangChain4j 正是为解决这一困境而诞生,它旨在借助 LLM 的强大效能,增强 Java 应用,简化 LLM 功能在Java应用中的…...

JDK 21 的新特性有哪些?带你全面解读 Java 的未来
引言:从 JDK 21 看 Java 的进化之路 Java 是一门历久弥新的语言,每一次版本更新都在强化它的生态体系。2023 年发布的 JDK 21,作为长期支持版本(LTS),带来了许多令人兴奋的新特性。不论你是开发者、架构师…...

【C++算法】53.链表_重排链表
文章目录 题目链接:题目描述:解法C 算法代码: 题目链接: 143. 重排链表 题目描述: 解法 模拟 找到链表的中间节点 快慢双指针 把后面的部分逆序 双指针,三指针,头插法 合并两个链表 合并两个有…...

多卡分布式训练:torchrun --nproc_per_node=5
多卡分布式训练:torchrun --nproc_per_node=5 1. torchrun 实现规则 torchrun 是 PyTorch 提供的用于启动分布式训练作业的实用工具,它基于 torch.distributed 包,核心目标是简化多进程分布式训练的启动和管理。以下是其主要实现规则: 进程启动 多进程创建:torchrun 会…...

系统架构设计师之系统设计模块笔记
一、系统设计概述 定义与目标 系统设计是根据系统分析结果,制定系统构建蓝图的过程,核心目标是合理分配功能需求、优化资源使用、确保系统高内聚低耦合,并满足性能、安全、可扩展等非功能需求。主要内容 概要设计:将功能需求分配…...

Elasticsearch:加快 HNSW 图的合并速度
作者:来自 Elastic Thomas Veasey 及 Mayya Sharipova 过去,我们曾讨论过搜索多个 HNSW 图时所面临的一些挑战,以及我们是如何缓解这些问题的。当时,我们也提到了一些计划中的改进措施。本文正是这项工作的成果汇总。 你可能会问…...

图片中文字无法正确显示的解决方案
图片中文字无法正确显示的解决方案 问题描述 在 Linux 系统中生成图片时,图片中的文字(如中文)未能正确显示,可能表现为乱码或空白。这通常是由于系统缺少对应的字体文件(如宋体/SimSun),或者…...

数据结构:通俗解释AOE 网中事件的最早发生时间和最迟发生时间
1. 事件的最早发生时间 在 AOE 网(Activity On Edge Network,边表示活动的网络)中,事件的最早发生时间指从源点(起点)到该事件结点的最长路径长度(即所需时间)。它决定了所有以该事…...

C# 看门狗策略实现
using System; using System.Threading;public class Watchdog {private Timer _timer;private volatile bool _isTaskAlive;private readonly object _lock new object();private const int CheckInterval 5000; // 5秒检测一次private const int TimeoutThreshold 10000; …...
