算法训练之动态规划(三)

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥
♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥
♥♥♥我们一起努力成为更好的自己~♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥
✨✨✨✨✨✨ 个人主页✨✨✨✨✨✨
接下来这篇博客我们将继续在题目中使用巧妙的动态规划思想~准备好了吗~我们发车去探索奥秘啦~🚗🚗🚗🚗🚗🚗
下降路径的最小和
下降路径的最小和



这个题目看起来有点吓人,别怕,接下来我们一步步按照动态规划的思想来解决这道问题~
分析:
1、状态表示
结合这里的题目要求+经验:我们这里的状态表示——dp[i][j]为到达该位置的最小路径和
2、状态转移方程
我们以离【i】【j】位置最近的状态分析状态转移方程(题目要求最多相隔一列)所以有下面的三种情况:
1、到达该位置,可能是从第【i-1】【j】位置向下一步到达的
2、到达该位置,可能是从第【i-1】【j-1】位置向下再向右一步到达的
3、到达该位置,可能是从第【i-1】【j+1】位置向下再向左一步到达的
所以到达该位置最小路径和也就是三种情况的最小值再加上当前位置的数据(注意下标映射关系),所以状态转移方程也就是:
dp[i][j]=min(min(dp[i-1][j],dp[i-1][j-1]),dp[i-1][j+1]) + nums[i-1][j-1]
3、初始化
我们可以看到,状态转移方程里面有i-1,j-1,j+1当i=0或者j=0或者j=n的时候显然会出现越界的情况,所以我们需要进行初始化
结合前面如果不想初始化太麻烦,我们可以多申请一些空间,这里与前面不一样的是这里是我们这里还有一个j+1,那么我们这里也就可以多申请一行两列~那么怎么初始化这一行两列呢?
我们结合例子来看看:
我们首先来看看结合我们的逻辑dp[i][j]里面的值在具体的例子中是多少?
我们可以看到第一行就是它本身的值,而第一行是受到我们增加的那一行影响的,所以我们增加的那一行应该全部初始化为0,才不会出错~接下来看后面的两行,都是在取上一行三个位置的最小值加上当前位置值得到的,那么旁边的两列如果也初始化为0的话,那么边界找到的最小值就是0了,这并不是数组里面的有效数据~所以为了避免影响,我们也就可以把两列位置设置成INT_MAX,题目给出数据大小范围,显然dp[i][j]是不会超过INT_MAX的,那么我们就可以这样进行初始化~
第一行初始化为0,剩下的位置初始化为INT_MAX
这种初始化方式还需要注意的是下标的映射关系~
4、填表顺序
我们这里的逻辑是从上面依次推出下面的,所以填表顺序是从上向下
5、返回结果
这里返回结果也与我们前面的不一样,因为它不是一个具体的位置,最小路径和存在于最后一行,所以我们可以找到dp表最后一行最小值进行返回~
代码实现:
class Solution
{
public:int minFallingPathSum(vector<vector<int>>& matrix) {//1、创建dp表int m=matrix.size();int n=matrix[0].size();//多创建一行两列vector<vector<int>> dp(m+1,vector<int>(n+2,INT_MAX));//最开始就把所有位置初始化为INT_MAX//2、初始化//最开始就把所有位置初始化为INT_MAX了//初始化第一行为0for(int j=0;j<=n+1;j++){dp[0][j]=0;}//3、填表for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];//注意下标映射关系}}//4、返回结果//找到最后一行最小值进行返回int ret=dp[m][1];for(int i=2;i<=n;i++){ret=min(ret,dp[m][i]);}return ret;}
};
顺利通过~分析之后也就十分清楚了,我们来看看下一道题目~
最小路径和
最小路径和


我们同样可以一步步来分析:
1、状态表示
结合这里的题目要求+经验:我们这里的状态表示——dp[i][j]为到达该位置的最小总和
2、状态转移方程
我们以离【i】【j】位置最近的状态分析状态转移方程(题目要求只能向下或者向右移动)所以有下面的两种情况:
1、到达该位置,可能是从第【i-1】【j】位置向下一步到达的
2、到达该位置,可能是从第【i】【j-1】位置向右一步到达的
所以到达该位置最小总和也就是两种情况的最小值再加上当前位置的数据(注意下标映射关系),所以状态转移方程也就是:
dp[i][j]=min(dp[i-1][j],dp[i][j-1]) + nums[i-1][j-1]
3、初始化
我们可以看到,状态转移方程里面有i-1,j-1当i=0或者j=0的时候显然会出现越界的情况,所以我们需要进行初始化
结合前面如果不想初始化太麻烦,我们可以多申请一些空间,那么我们这里结合经验也就可以多申请一行一列~那么怎么初始化这一行一列呢?
我们结合例子来看看:
我们首先来看看结合我们的逻辑dp[i][j]里面的值在具体的例子中是多少?
我们可以看到除了左上角的数就是它本身的值,其他的值都发生了变化,而左上角的数是受到它上面的位置和左边的位置影响的,结合状态转移方程 dp[i][j]=min(dp[i-1][j],dp[i][j-1]) + nums[i-1][j-1],所以它上面的位置和左边的位置应该初始化为0,才不会出错~接下来看剩下的位置,每一个位置都是在取当前位置上面的位置和左边的位置的最小值加上当前位置值得到的,那么如果也初始化为0的话,那么边界找到的最小值就是0了,这并不是数组里面的有效数据~所以为了避免影响,我们也就可以把剩下的设置成INT_MAX,题目给出数据大小范围,显然dp[i][j]是不会超过INT_MAX的,那么我们就可以这样进行初始化~
dp[1][0]=dp[0][1]=0,剩下的位置初始化为INT_MAX
这种初始化方式还需要注意的是下标的映射关系~
4、填表顺序
我们这里的逻辑是从上面依次推出下面的,所以填表顺序是从上向下
5、返回结果
右下角的位置就是我们想要的结果,直接返回dp[m][n]就可以了
有了前面题目的铺垫,相信这道题目就手到擒来了~
代码实现:
class Solution
{
public:int minPathSum(vector<vector<int>>& grid) {//1、创建dp表int m=grid.size();int n=grid[0].size();//dp表最开始全部初始化为INT_MAXvector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//2、初始化dp[0][1]=dp[1][0]=0;//3、填表for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];//注意下标映射关系}}//4、返回结果return dp[m][n];}
};
顺利通过~
地下城游戏
地下城游戏


一看这题目就有点吓人,我们同样按照我们之前的步骤来进行分析:
1、状态表示
结合这里的题目要求+经验:状态表示一般有两种方式:
1、以某一个位置为结尾分析:
我们这里来看看如果我们以【i】【j】位置为结尾来分析的话,认为dp【i】【j】表示的是到该位置的最低健康点数,那么我们可以发现dp【i】【j】不仅仅受到前面位置的影响,还会受到后面位置的影响,这样就会十分麻烦,所以我们换一种方式~
2、以某一个位置为起点分析:
我们这里来看看如果我们以【i】【j】位置为起点来分析的话,认为dp【i】【j】表示的是从该位置开始到达指定位置的最低健康点数,那么dp【i】【j】只受到后面位置的影响,这样就更加方便~
2、状态转移方程
我们以离【i】【j】位置最近的状态分析状态转移方程(题目要求只能向下或者向右移动)所以有下面的两种情况:
1、以该位置为起点,可能是向下一步到达第【i+1】【j】位置
2、以该位置为起点,可能是向右一步到达第【i】【j+1】位置
所以dp【i】【j】也就是以该位置为起点,两种情况的最小值再减去当前位置的数据(这里增加不需要注意下标映射关系),所以状态转移方程也就是:
dp[i][j]=min(dp[i+1][j],dp[i][j+1]) - nums[i][j]
这样处理之后,还有一种情况就是dp[i][j]是负数了,也就是nums[i][j]很大,那么该位置的最小健康点数只需要是1经过加上nums[i][j]就可以了,所以还需要处理为负数的情况~
dp[i][j]=max(1,dp[i][j])
3、初始化
我们可以看到,状态转移方程里面有i+1,j+1当i=m-1或者j=n-1的时候显然会出现越界的情况,所以我们需要进行初始化
结合前面如果不想初始化太麻烦,我们可以多申请一些空间,那么我们这里结合经验也就可以多申请一行一列~与前面不同的是这里是以【i】【j】位置为起点来分析,所以加的那一行一列在后面,那么怎么初始化这一行一列呢?
我们结合例子来看看:
我们首先来看看结合我们的逻辑dp[i][j]里面的值在具体的例子中是多少?
我们可以看到除了右下角的数到达右边或者下边那一个位置至少还应该剩下1的健康点数,不能刚好到了就死亡了,所以dp【m-1】【n】=dp【m】【n-1】=1,接下来看剩下的位置,每一个位置都是在取当前位置下面的位置和右边的位置的最小值加上当前位置值得到的,那么如果也初始化为1的话,那么边界找到的最小值就是错误的~所以为了避免影响,我们也就可以把剩下的设置成INT_MAX,题目给出数据大小范围,显然dp[i][j]是不会超过INT_MAX的,那么我们就可以这样进行初始化~
dp[m-1][n]=dp[m][n-1]=1,剩下的位置初始化为INT_MAX
这种初始化方式还不需要注意下标的映射关系了~因为位置与数组一一对应的~
4、填表顺序
我们这里的逻辑是从下面/右边依次推出上面/左边的,所以填表顺序是从下向上,从右向左
5、返回结果
左上角的位置就是我们想要的结果,直接返回dp[0][0]就可以了
代码实现:
class Solution
{
public:int calculateMinimumHP(vector<vector<int>>& d) {//1、创建dp表int m=d.size();int n=d[0].size();//最开始全部初始化为INT_MAXvector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//2、初始化dp[m-1][n]=dp[m][n-1]=1;//3、填表//注意填表顺序for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])-d[i][j];//处理为负的情况dp[i][j]=max(1,dp[i][j]);}}//4、返回结果return dp[0][0];}
};
顺利通过~
♥♥♥本篇博客内容结束,期待与各位优秀程序员交流,有什么问题请私信♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨
相关文章:

算法训练之动态规划(三)
♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥ ♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥ ♥♥♥我们一起努力成为更好的自己~♥♥♥ ♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥ ♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥ ✨✨✨✨✨✨ 个…...

xv6-labs-2024 lab2
lab-2 0. 前置 课程记录 操作系统的隔离性,举例说明就是,当我们的shell,或者qq挂掉了,我们不希望因为他,去影响其他的进程,所以在不同的应用程序之间,需要有隔离性,并且࿰…...
)
LangChain-模型输入输出 (Model I/O)
模型输入输出是LangChain的核心组件,负责处理与各种语言模型的交互。本文档详细介绍了这些组件的功能和使用方法。 概述 模型输入输出组件负责: 连接各种语言模型:统一不同提供商的模型接口格式化输入:将原始输入转换为模型可理…...

基于FPGA实现BPSK 调制
目录 一、 任务介绍二、基本原理三、基于FPGA实现BPSK 调制四、源码 一、 任务介绍 BPSK 调制在数字通信系统中是一种极重要的调制方式,它的抗干扰噪声性能及通频带的利用率均优先于 ASK 移幅键控和 FSK 移频键控。因此,PSK 技术在中、高速数据传输中得…...

深入理解 ResponseBodyAdvice 及其应用
ResponseBodyAdvice 是 Spring MVC 提供的一个强大接口,允许你在响应体被写入 HTTP 响应之前对其进行全局处理。 下面我将全面介绍它的工作原理、使用场景和最佳实践。 基本概念 接口定义 public interface ResponseBodyAdvice<T> {boolean supports(Metho…...
)
Java 基础 - 反射(1)
文章目录 引入类加载过程1. 通过 new 创建对象2. 通过反射创建对象2.1 触发加载但不初始化2.2 按需触发初始化2.3 选择性初始化控制 核心用法示例1. 通过无参构造函数创建实例对象2. 通过有参构造函数创建实例对象3. 反射通过私有构造函数创建对象, 破坏单例模式4. …...

Spring Boot中Spring MVC相关配置的详细描述及表格总结
以下是Spring Boot中Spring MVC相关配置的详细描述及表格总结: Spring MVC 配置项详解 1. 异步请求配置 spring.mvc.async.request-timeout 描述:设置异步请求的超时时间(单位:毫秒)。默认值:未设置&…...

flink Shuffle的总结
关于 ** 5 种 Shuffle 类型** 的区别、使用场景及 Flink 版本支持的总结: * 注意:下面是问AI具体细节与整理学习 1. 核心区别 Shuffle 类型核心特点使用场景Flink 版本支持Pipelined Shuffle流式调度,纯内存交换,低延迟(毫秒级…...

在排序数组中查找元素的第一个和最后一个位置 --- 二分查找
目录 一:题目 二:算法原理分析 三:代码实现 一:题目 题目链接: 34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode) 二:算法原理分析 三:代码实现 c…...
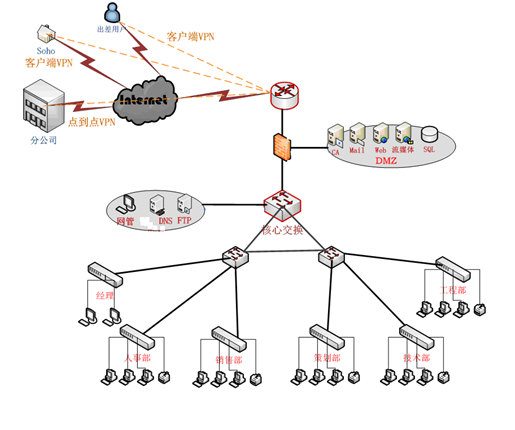
631SJBH中小型企业的网络管理模式的方案设计
1.1、研究现状 我国很多企业信息化水平一直还处在非常初级的阶段,有关统计表明,真正实现了计算机较高应用的企业在全国1000多万中小企业中所占的比例还不足10%幢3。大多数企业还停留在利用互联网进行网上查询(72.9%)、…...
)
NO.85十六届蓝桥杯备战|动态规划-经典线性DP|最长上升子序列|合唱队形|最长公共子序列|编辑距离(C++)
经典线性dp问题有两个:最⻓上升⼦序列(简称:LIS)以及最⻓公共⼦序列(简称:LCS),这两道题⽬的很多⽅⾯都是可以作为经验,运⽤到别的题⽬中。⽐如:解题思路&…...

0410 | 软考高项笔记:项目管理概述
以下是不同组织结构中项目经理的角色、工作特点以及快速记忆的方法: 不同组织结构中项目经理的角色和工作特点 组织结构项目经理的角色工作特点职能型组织项目协调者、辅助管理者权力有限,主要负责协调部门间的工作,项目成员向部门经理汇报…...

Vue3的Composition API与React Hooks有什么异同?
Vue3的一个重大更新点就是支持Composition API,而且也被业界称为hooks,那么Vue3的“Hooks”与React的Hooks有这么区别呢? 一、核心相似点 1. 逻辑复用与代码组织 都解决了传统类组件或选项式 API 中逻辑分散的问题,允许将相关逻…...

LangChain4j(1):初步认识Java 集成 LLM 的技术架构
LangChain 作为构建具备 LLM 能力应用的框架,虽在 Python 领域大放异彩,但 Java 开发者却只能望洋兴叹。LangChain4j 正是为解决这一困境而诞生,它旨在借助 LLM 的强大效能,增强 Java 应用,简化 LLM 功能在Java应用中的…...

JDK 21 的新特性有哪些?带你全面解读 Java 的未来
引言:从 JDK 21 看 Java 的进化之路 Java 是一门历久弥新的语言,每一次版本更新都在强化它的生态体系。2023 年发布的 JDK 21,作为长期支持版本(LTS),带来了许多令人兴奋的新特性。不论你是开发者、架构师…...

【C++算法】53.链表_重排链表
文章目录 题目链接:题目描述:解法C 算法代码: 题目链接: 143. 重排链表 题目描述: 解法 模拟 找到链表的中间节点 快慢双指针 把后面的部分逆序 双指针,三指针,头插法 合并两个链表 合并两个有…...

多卡分布式训练:torchrun --nproc_per_node=5
多卡分布式训练:torchrun --nproc_per_node=5 1. torchrun 实现规则 torchrun 是 PyTorch 提供的用于启动分布式训练作业的实用工具,它基于 torch.distributed 包,核心目标是简化多进程分布式训练的启动和管理。以下是其主要实现规则: 进程启动 多进程创建:torchrun 会…...

系统架构设计师之系统设计模块笔记
一、系统设计概述 定义与目标 系统设计是根据系统分析结果,制定系统构建蓝图的过程,核心目标是合理分配功能需求、优化资源使用、确保系统高内聚低耦合,并满足性能、安全、可扩展等非功能需求。主要内容 概要设计:将功能需求分配…...

Elasticsearch:加快 HNSW 图的合并速度
作者:来自 Elastic Thomas Veasey 及 Mayya Sharipova 过去,我们曾讨论过搜索多个 HNSW 图时所面临的一些挑战,以及我们是如何缓解这些问题的。当时,我们也提到了一些计划中的改进措施。本文正是这项工作的成果汇总。 你可能会问…...

图片中文字无法正确显示的解决方案
图片中文字无法正确显示的解决方案 问题描述 在 Linux 系统中生成图片时,图片中的文字(如中文)未能正确显示,可能表现为乱码或空白。这通常是由于系统缺少对应的字体文件(如宋体/SimSun),或者…...

数据结构:通俗解释AOE 网中事件的最早发生时间和最迟发生时间
1. 事件的最早发生时间 在 AOE 网(Activity On Edge Network,边表示活动的网络)中,事件的最早发生时间指从源点(起点)到该事件结点的最长路径长度(即所需时间)。它决定了所有以该事…...

C# 看门狗策略实现
using System; using System.Threading;public class Watchdog {private Timer _timer;private volatile bool _isTaskAlive;private readonly object _lock new object();private const int CheckInterval 5000; // 5秒检测一次private const int TimeoutThreshold 10000; …...
 操作系统上添加 ollama 作为系统服务的步骤)
在 openEuler 24.03 (LTS) 操作系统上添加 ollama 作为系统服务的步骤
以下是在 openEuler 操作系统上添加 ollama 作为系统服务的步骤: 创建 systemd 服务文件 sudo vi /etc/systemd/system/ollama.service将以下内容写入服务文件(按需修改参数): [Unit] DescriptionOllama Service Afternetwork.…...

Elasticsearch中的基本全文搜索和过滤
Elasticsearch中的基本全文搜索和过滤 知识点参考: https://www.elastic.co/guide/en/elasticsearch/reference/current/full-text-filter-tutorial.html#full-text-filter-tutorial-range-query 1. 索引设计与映射 多字段类型(Multi-Fields) ÿ…...

基于VSCode的Qt开发‘#include ui_test.h’报错没有该文件
笔者在基于VSCode进行Qt开发时,test.ui文件是在Qt软件中绘制的,导致本项目无法使用这个ui文件,报错如标题。事实上,本工程中也确实没有生成这个头文件。出现这个错误的原因是ui文件没有被编译为c头文件。 要生成 ui_test.h 文件&…...

Python常用排序算法
1. 冒泡排序 冒泡排序是一种简单的排序算法,它重复地遍历要排序的列表,比较相邻的元素,如果他们的顺序错误就交换他们。 def bubble_sort(arr):# 遍历所有数组元素for i in range(len(arr)):# 最后i个元素是已经排序好的for j in range(0, …...

ISP--Demosaicking
文章目录 前言算法解释简单的线性插值代码实现 色差法和色比法基于方向加权的方法RB缺失的G通道的插值RB缺失的BR的插值G缺失的BR的插值代码实现 基于边缘检测的方法计算缺失的G计算缺失的RB值/计算缺失的G值 前言 人眼之所以有能感受到自然界的颜色,是因为人眼的感…...

国标GB28181协议EasyCVR视频融合平台:5G时代远程监控赋能通信基站安全管理
一、背景介绍 随着移动通信行业的迅速发展,无人值守的通信基站建设规模不断扩大。这些基站大多建于偏远地区,周边人迹罕至、交通不便,给日常的维护带来了极大挑战。其中,位于空旷地带的基站设备,如空调、蓄电池等&…...

vue watch 和 watchEffect的区别和用法
在 Vue.js 里,watch 和 watchEffect 都用于响应式地追踪数据变化并执行相应操作,不过它们在使用方式、应用场景等方面存在差异。 1. watch watch 是 Vue 提供的一个选项,用于监听特定数据的变化。当监听的数据发生变化时,会触发…...

SQL 不走索引的常见情况
在 SQL 查询中,即使表上有索引,某些情况下数据库优化器也可能决定不使用索引。以下是常见的不走索引的情况: 1. 使用否定操作符 NOT IN ! 或 <> NOT EXISTS NOT LIKE 2. 对索引列使用函数或运算 -- 不走索引 SELECT * FROM user…...









