神经网络基础[ANN网络的搭建]
神经网络
人工神经网络( Artificial Neural Network, 简写为ANN)也简称为神经网络(NN),是一种模仿生物神经网络结构和功能的计算模型。各个神经元传递复杂的电信号,树突接收到输入信号,然后对信号进行处理,通过轴突输出信号。下图是生物神经元示意图:
- 是一种计算模型
- 简称:NN

当电信号通过树突进入到细胞核时,会逐渐聚集电荷。达到一定的电位后,细胞就会被激活,通过轴突发出电信号。
NN
神经网络中信息只向一个方向移动,即从输入节点向前移动,通过隐藏节点,再向输出节点移动。其中的基本部分是:
1.输入层: 即输入 x 的那一层
2.输出层: 即输出 y 的那一层
3.隐藏层: 输入层和输出层之间都是隐藏层[作用:加权求和+激活]
特点
•同一层的神经元之间没有连接。
•第 N 层的每个神经元和第 N-1层 的所有神经元相连(这就是full connected的含义),这就是全连接神经网络。
•第N-1层神经元的输出就是第N层神经元的输入。
•每个连接都有一个权重值(w系数和b系数)。

激活函数
激活函数的作用
激活函数用于对 每层 的输出数据进行变换, 进而为整个网络注入了非线性因素。此时, 神经网络就可以拟合各种曲线。

如果不使用激活函数,无论网络搭建得再复杂也是线性模型
常用的激活函数
f ( x ) = 1 1 + e − x f(x) = \frac{1} {1 + e^{-x}} f(x)=1+e−x1
导函数公式
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x) = f(x)(1 - f(x)) f′(x)=f(x)(1−f(x))
图像

f(x):定义域: (-∞,+∞)值域:(0,1)
有效区间:[-6,6]
f'(x)值域:(0,0.25]
不足:计算量大
一般来说, sigmoid 网络在5 层之内就会产生梯度消失现象。而且,该激活函数并不是以 0 为中心的,所以在实践中这种激活函数使用的很少
-
tanh
类似sigmoid
f ( x ) = e x − e − x e x + e − x = 1 − e − 2 x 1 + e − 2 x f(x) =\frac{e^x - e^{-x}}{e^x + e^{-x}}=\frac{1 - e^{-2x}}{1 + e^{-2x}} f(x)=ex+e−xex−e−x=1+e−2x1−e−2x
f ′ ( x ) = 1 − f 2 ( x ) f'(x) = 1 - f^2(x) f′(x)=1−f2(x)
f(x):值域:(-1,1)有效区间:[-3,3] 特点:- 收敛速度比sigmoid快- 存在梯度消失问题图像

-
softmax
softmax用于多分类过程中,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来。计算方法如下所示
s o f t m a x ( z i ) = e z i Σ j e z j softmax(z_i) = \frac{e ^ {z_i}}{Σ_j e ^{z_j}} softmax(zi)=Σjezjezi -
ReLu
f ( x ) = m a x ( 0 , x ) f(x) = max(0,x) f(x)=max(0,x)
f ′ ( x ) = { 0 , x < 0 1 , x ≥ 0 f'(x) = \begin{cases}0 & {,x < 0}\\1 & ,x \geq 0 \end{cases} f′(x)={01,x<0,x≥0
优点:- 计算量小,是最常用的一种激活函数- Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。 缺点:- 存在 '神经元死亡' 问题
随着训练的推进,部分输入会落入小于0区域,导致对应权重无法更新。这种现象被称为 神经元死亡。
图像
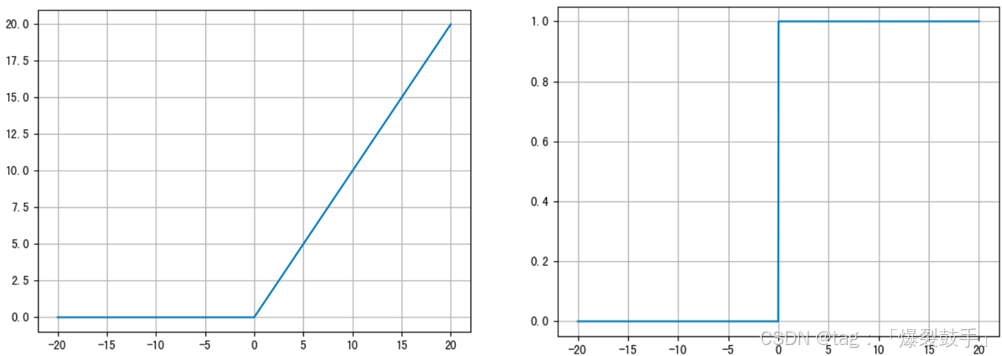
-
Leaky ReLu(见下图)
-
ELU
ELU是对ReLu的改进,是对 ReLu(Rectified Linear Unit)的一种改进,旨在克服 ReLU 神经元死亡的问题.具体而言是通过定义了一个指数负区间来代替0值.
f ( x ) = { x , x > 0 α ( e x − 1 ) , x ≤ 0 f(x)=\begin{cases}x & {,x>0}\\ α(e^x−1) & {,x≤0} \end{cases} f(x)={xα(ex−1),x>0,x≤0 -
Celu
CELU(Continuously Differentiable Exponential Linear Unit)是 ELU(Exponential Linear Unit)的一个扩展,它通过对负值区域引入一个平滑的连续函数,进一步改善了神经元死亡问题,并增强了激活函数的灵活性。CELU 激活函数的设计目的是避免 ReLu 的死区问题,同时具备与 ELU 类似的平滑行为,但是具有一个可调的平滑程度。
f ( x ) = { x , if x > 0 α ( e x α − 1 ) , if x ≤ 0 f(x) = \begin{cases} x, & \text{if } x > 0 \\ \alpha (e^{\frac{x}{\alpha}} - 1), & \text{if } x \leq 0 \end{cases} f(x)={x,α(eαx−1),if x>0if x≤0 -
Identity(恒等激活)(见下图)
-
其他激活函数

代码
def show(activation, *args):""":param activation: (激活函数:接收其内存地址) torch.sigmoid | torch.tanh | torch.relu:return: None"""_, axes = plt.subplots(1, 2)x = torch.linspace(-20, 20, 1000)y = activation(x)axes[0].plot(x, y)axes[0].grid()axes[0].set_title(str(activation).split(' ')[2])x = torch.linspace(-20, 20, 1000, requires_grad=True)print(activation(x, *args).sum())activation(x, *args).sum().backward()axes[1].plot(x.detach(), x.grad)axes[1].grid()axes[1].set_title(f"{str(activation).split(' ')[2]}'s Derived")plt.show()def softmax_show():""":return:"""score = torch.tensor([0.2, 0.02, 0.15, 0.15, 0.15, 0.15, 1, 3.14])probabilities = torch.softmax(score, dim=0)print(probabilities)print(sum(probabilities))def elu():elu = torch.nn.ELU(alpha=1)_, axes = plt.subplots(1, 2)x = torch.linspace(-40, 40, 1000)y = elu(x)axes[0].plot(x, y)axes[0].grid()axes[0].set_title('elu')x = torch.linspace(-40, 40, 1000, requires_grad=True)print(elu(x).sum())elu(x).sum().backward()axes[1].plot(x.detach(), x.grad)axes[1].grid()axes[1].set_title(f"elu's Derived")plt.show()if __name__ == '__main__':# show(torch.sigmoid)# show(torch.tanh)# show(torch.relu)# show(torch.celu, 0.001)softmax_show()
参数的初始化
在神经网络中,参数初始化(Parameter Initialization)指的是在训练开始之前设置网络权重(weights)和偏置(biases)的初始值。合适的初始化策略对于神经网络的训练过程至关重要。好的初始化方法能够加速收敛,提高模型的性能,避免一些常见的问题,如梯度消失或梯度爆炸。
参数初始化的作用
- 加速收敛:
- 一个好的初始化策略能帮助模型更快地收敛。合适的初始化会避免在训练初期陷入困境,使得梯度在反向传播时不会因为初始值太小或太大而导致学习困难。
- 避免梯度消失和梯度爆炸:
- 如果初始化过小或过大,可能导致梯度在反向传播时变得非常小(梯度消失)或非常大(梯度爆炸),从而影响训练的稳定性。
- 例如,深度网络中的梯度消失问题会导致模型训练速度极慢,甚至无法更新参数;而梯度爆炸则可能导致训练过程中权重更新过快,导致权重的值极大,进而造成不稳定的训练。
- 确保每个神经元有不同的学习路径:
- 如果所有神经元的初始权重相同,那么每个神经元将执行相同的操作,导致它们在训练过程中学习到相同的特征,这会大大降低模型的表现。
- 通过合理的初始化方法,确保每个神经元从不同的初始值开始学习,使得它们能学习到不同的特征,提高模型的多样性和表现。
- 避免对称性破坏:
- 如果所有权重被初始化为相同的值,所有神经元的输出也将相同,导致网络在训练过程中无法破除对称性,使得每个神经元的更新是一样的,无法发挥出网络的深度特性。合理初始化权重能够避免这一问题。
基本初始化
-
均匀分布初始化
权重参数初始化从区间均匀随机取值。即在(-1/√d,1/√d)均匀分布中生成当前神经元的权重,其中d为每个神经元的输入数量
-
正态分布初始化
随机初始化从均值为0,标准差是1的高斯分布中取样,使用一些很小的值对参数W进行初始化
-
全0初始化
将神经网络中的所有权重参数初始化为 0
-
全1初始化
将神经网络中的所有权重参数初始化为 1.
-
固定值初始化
将神经网络中的所有权重参数初始化为某个固定值.
示例
import torch
import torch.nn as nn# 1.均匀分布初始化
def test01():linear = nn.Linear(5, 3)# 从 0-1的均匀分布产生参数nn.init.uniform_(linear.weight)print(linear.weight.data)# 2.固定初始化
def test02():linear = nn.Linear(5, 3)nn.init.constant_(linear.weight, 5)print(linear.weight.data)# 3. 全0初始化
def test03():linear = nn.Linear(5, 3)nn.init.zeros_(linear.weight)print(linear.weight.data)# 4. 全1初始化
def test04():linear = nn.Linear(5, 3)nn.init.ones_(linear.weight)print(linear.weight.data)# 5.正态分布随机初始化
def test05():linear = nn.Linear(5, 3)nn.init.normal_(linear.weight, mean=0.0, std=1.0)print(linear.weight.data)
常用初始化
-
kaiming 初始化,也叫做 HE 初始化
1.正态化的he初始化
stddev = sqrt(2 / fan_in)
2.均匀分布的he初始化
它从 [-limit,limit] 中的均匀分布中抽取样本, limit是 sqrt(6 / fan_in)fan_in 输入神经元的个数
-
xavier 初始化,也叫做 Glorot初始化
1.正态化的Xavier初始化
stddev = sqrt(2 / (fan_in + fan_out))
2.均匀分布的Xavier初始化
从[-limit,limit] 中的均匀分布中抽取样本, limit 是 sqrt(6 / (fan_in + fan_out))fan_in 是输入神经元的个数, fan_out 是输出的神经元个数
代码:
# 6.kaiming初始化
def test06():linear = nn.Linear(5, 3)nn.init.kaiming_normal_(linear.weight)print(f'kaiming标准正态初始化:{linear.weight.data}')nn.init.uniform_(linear.weight)print(f'kaiming均匀分布初始化:{linear.weight.data}')# 7.xavier初始化
def test07():linear = nn.Linear(5, 3)nn.init.xavier_normal_(linear.weight)print(f'xavier标准正态初始化:{linear.weight.data}')nn.init.xavier_uniform_(linear.weight)print(f'xavier均匀分布初始化:{linear.weight.data}')
神经网络的搭建
在PyTorch中定义深度神经网络其实就是层堆叠的过程
1.自定义类,继承自nn.Module
2.实现两个方法:__init__方法:定义网络中的层结构,主要是全连接层,并进行初始化 - 作用:[定义网络层]forward方法:在实例化模型的时候,底层会自动调用该函数。该函数中可以定义学习率,为初始化定义的layer传入数据等。 - 作用:[串联网络层]
示例:搭建如图所示的神经网络

编码设计如下:
1.第1个隐藏层:权重初始化采用标准化的xavier初始化 激活函数使用sigmoid
2.第2个隐藏层:权重初始化采用标准化的He初始化 激活函数采用relu
3.out输出层线性层:假若二分类,采用softmax做数据归一化
思路说明:

代码实现:
import torch
import torch.nn as nn
from torchsummary import summary # 计算参数模型# 1.创建神经网络模块
# 1.1 一个继承
class Model(nn.Module):# 1.2 两个方法 __init__ forwarddef __init__(self):super(Model, self).__init__() # 调用父类的初始化属性方法# 创建第一个隐藏层self.linear1 = nn.Linear(3, 3)nn.init.xavier_normal_(self.linear1.weight)# 创建第二个隐藏层self.linear2 = nn.Linear(3, 2)# kaiming初始化nn.init.kaiming_normal_(self.linear2.weight)# 创建输出层模型self.out = nn.Linear(2, 2)def forward(self, x):# 数据经过第一个线性层x = self.linear1(x)# 使用sigmoid激活x = torch.sigmoid(x)# 数据经过第二个线性层x = self.linear2(x)# 使用relu激活x = torch.relu(x)# 数据经过输出层x = self.out(x)# 使用softmax激活# dim = -1: 每一个维度的行数据 相加为1x = torch.softmax(x, dim=-1)return x
使用网络
model = Model()# 随机产生一组数据
data = torch.randn(5, 3)
print(f'data.shape->{data.shape}')# 前向传播
output = model(data)
print(f'output.shape->:{output.shape}')# 计算模型参数
summary(model, input_size=(3,), batch_size=5)# 查看模型参数
print('=' * 20 + '查看模型参数' + '=' * 20)
for name, parameter in model.named_parameters():print(name, parameter)
神经网络总结
1.优点
-
精度高,性能优于其他的机器学习算法,甚至在某些领域超过了人类
-
可以近似任意的非线性函数
-
近年来在学界和业界受到了热捧,有大量的框架和库可供调。
2.缺点
-
黑箱,很难解释模型是怎么工作的
-
训练时间长,需要大量的计算资源
-
网络结构复杂,需要调整超参数
-
部分数据集上表现不佳,容易发生过拟合
相关文章:

神经网络基础[ANN网络的搭建]
神经网络 人工神经网络( Artificial Neural Network, 简写为ANN)也简称为神经网络(NN),是一种模仿生物神经网络结构和功能的计算模型。各个神经元传递复杂的电信号,树突接收到输入信号…...
五、web自动化测试01
目录 一、HTML基础1、HTML介绍2、常用标签3、基础案例3.1 前端代码3.2 自动化测试 二、CSS定位1、css介绍2、案例3、代码优化 三、表单自动化1、案例2、元素属性定位 四、后台基础数据自动化1、登录1.1 id与class定位1.2 定位一组元素 2、商品新增 一、HTML基础 可参考学习 链…...

数据库监控 | MongoDB监控全解析
PART 01 MongoDB:灵活、可扩展的文档数据库 MongoDB作为一款开源的NoSQL数据库,凭借其灵活的数据模型(基于BSON的文档存储)、水平扩展能力(分片集群)和高可用性(副本集架构)&#x…...

STM32F407使用ESP8266实现阿里云OTA(中)
文章目录 前言一、程序分析二、程序讲解1. main函数2. Get_Version()函数3. esp_Init()函数4. Check_Updata()函数结语前言 从上一章STM32F407使用ESP8266实现阿里云OTA(上)中我们已经对连接阿里云和从阿里云获取升级包的流程非常的熟悉了。所以本章我们进行STM32的程序开发…...

sql server 与navicat测试后,连接qt
先用Navicat测试和sql的连通性,Navicat和sql连通之后,qt也能和sql连通了。 Navicat和Sqlserver Management 能连上,项目无法连接本地 Navicat 连接SQLServer 数据库 QT国内镜像网站 Navicat连接SqlServer的问题点 Sql Server的基本配置以及使…...

Django 入门实战:从环境搭建到构建你的第一个 Web 应用
Django 入门实战:从环境搭建到构建你的第一个 Web 应用 恭喜你选择 Django 作为你学习 Python Web 开发的起点!Django 是一个强大、成熟且功能齐全的框架,非常适合构建中大型的 Web 应用程序。本篇将通过一个简单的例子,带你走完…...

ROS2---时间戳对齐
一、ROS2时间系统架构 时间模型 仿真时间(Simulation Time):由/clock话题驱动,适用于离线仿真与调试。真实时间(Real Time):基于系统硬件时钟,支持PTP协议(IEEE 1588&…...

Sublime Text相关设置
一直知道Sublime Text的自由度很高,但是之前使用从未更改过配置,有一天突然想改改设置试一下,感觉打开了新大陆,特此记录一下 设置默认语法 单击 Tools→Developer→New Snippet 弹出一个窗口,把下面这段代码粘贴进去…...

微信小程序 tabbar底部导航栏
官方文档:https://developers.weixin.qq.com/miniprogram/dev/reference/configuration/app.html#tabBar 一、常规菜单格式 在app.json 文件中配置,其他关键点详见官方文档,后续更新不规则图标的写法...

【Maven】项目管理工具
Maven:一个项目管理工具 前言 传统项目管理存在的问题: 依赖管理混乱 需要自己去网上搜 jar 包,找对版本很痛苦(还容易找错)某个库依赖另一个库(传递依赖),你得自己挨个找齐不小心…...

多线程事务?拿捏!
场景:有一批1万或者10万数据,插入数据库,怎么做 事务中进行批量提交 publList<List<OrderPo>> partition Lists.partition(list, 450);StopWatch stopWatch new StopWatch();stopWatch.start();// 顺序插入for (List<OrderPo> sub…...

Unity InputSystem触摸屏问题
最近把Unity打包后的windows软件放到windows触摸屏一体机上测试,发现部分屏幕触摸点击不了按钮,测试了其他应用程序都正常。 这个一体机是这样的,一个电脑机箱,外接一个可以触摸的显示屏,然后UGUI的按钮就间歇性点不了…...

Linux Awk 深度解析:10个生产级自动化与云原生场景
看图猜诗,你有任何想法都可以在评论区留言哦~ 摘要 Awk 作为 Linux 文本处理三剑客中的“数据工程师”,凭借字段分割、模式匹配和数学运算三位一体的能力,成为处理结构化文本(日志、CSV、配置文件)的终极工具。本文聚…...

免费版还是专业版?Dynadot 域名邮箱服务选择指南
关于Dynadot Dynadot是通过ICANN认证的域名注册商,自2002年成立以来,服务于全球108个国家和地区的客户,为数以万计的客户提供简洁,优惠,安全的域名注册以及管理服务。 Dynadot平台操作教程索引(包括域名邮…...

旋转磁体产生的场-对导航姿态的影响
pitch、yaw、roll是描述物体在空间中旋转的术语,通常用于计算机图形学或航空航天领域中。这些术语描述了物体绕不同轴旋转的方式: Pitch(俯仰):绕横轴旋转,使物体向前或向后倾斜。俯仰角度通常用来描述物体…...

动态哈希映射深度指南:从基础到高阶实现与优化
哈希表是计算机科学中最高效的数据结构之一,而动态哈希映射通过智能扩容机制,在实时系统中展现出极强的适应性。本文将深入探讨其实现细节,结合主流框架源码解析,并给出可落地的性能优化方案。 一、动态哈希的数学本质 1. 哈希函…...

Day11(回溯法)——LeetCode79.单词搜索
1 前言 今天主要刷了一道热题榜中回溯法的题,现在的计划是先刷热题榜专题吧,感觉还是这样见效比较快。因此本文主要介绍LeetCode79。 2 LeetCode79.单词搜索(LeetCode79) OK题目描述及相关示例如下: 2.1 题目分析解决及优化 感觉回溯的方…...
)
高精度并行2D圆弧拟合(C++)
依赖库 Eigen3 GLM Ceres-2.1.0 glog-0.6.0 gflag-2.2.2 基本思路 Step 1: RANSAC找到圆弧,保留inliers点; Step 2:使用ceres非线性优化的方法,拟合inliers点,得到圆心和半径; -------…...

Linux端口占用问题排查与解决
在 Linux 中,当遇到端口被占用的情况(如你遇到的 8000 端口),可以通过以下步骤查看并处理: 1. 查看占用端口的进程 使用 netstat 或 ss 命令(推荐 ss,更现代): sudo netstat -tulnp | grep :8000 # 或 sudo ss -tulnp | grep :8000输出示例: tcp 0 0 0.0.0.0:…...

PostgreSQL 分区表——范围分区SQL实践
PostgreSQL 分区表——范围分区SQL实践 1、环境准备1-1、新增原始表1-2、执行脚本新增2400w行1-3、创建pg分区表-分区键为创建时间1-4、创建24年所有分区1-5、设置默认分区(兜底用)1-6、迁移数据1-7、创建分区表索引 2、SQL增删改查测试2-1、查询速度对比…...
、A2A、数据库查询与信息检索的实现)
4.3 工具调用与外部系统集成:API调用、MCP(模型上下文协议)、A2A、数据库查询与信息检索的实现
工具调用与外部系统集成是智能代理(Agent)系统实现复杂功能和企业级应用的核心支柱。Agent通过API调用访问实时服务,**模型上下文协议(Model Context Protocol, MCP)**标准化数据交互,Agent-to-Agent&#…...
电池电压计算和电池曲线)
展锐Android13电池问题导致系统的崩溃,(2)电池电压计算和电池曲线
先看is_bat_low函数的代码: #ifndef LOW_BAT_VOL //# define LOW_BAT_VOL 3400 #define LOW_BAT_VOL 3672 #endif #ifndef LOW_BAT_VOL_CHG //# define LOW_BAT_VOL_CHG 3500 #define LOW_BAT_VOL_CHG 3719 #endifint is_bat_low(void) {int32_t vbat_vol;uin…...

SpringCloud 微服务复习笔记
文章目录 微服务概述单体架构微服务架构 微服务拆分微服务拆分原则拆分实战第一步:创建一个新工程第二步:创建对应模块第三步:引入依赖第四步:被配置文件拷贝过来第五步:把对应的东西全部拷过来第六步:创建…...
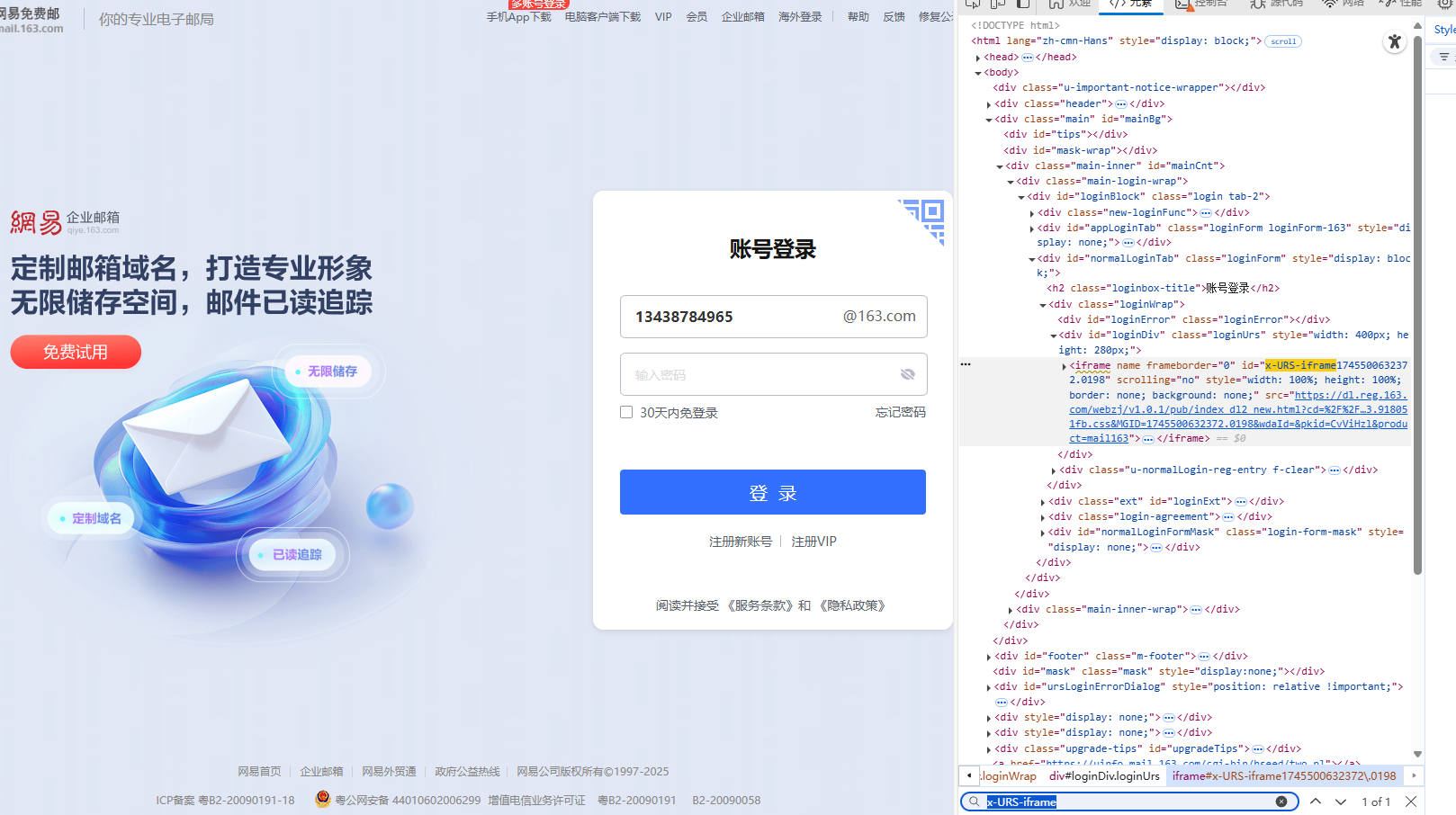
【Python爬虫基础篇】--4.Selenium入门详细教程
先解释:Selenium:n.硒;硒元素 目录 1.Selenium--简介 2.Selenium--原理 3.Selenium--环境搭建 4.Selenium--简单案例 5.Selenium--定位方式 6.Selenium--常用方法 6.1.控制操作 6.2.鼠标操作 6.3.键盘操作 6.4.获取断言信息 6.5.…...

【Python爬虫详解】第四篇:使用解析库提取网页数据——XPath
在前一篇文章中,我们介绍了如何使用BeautifulSoup解析库从HTML中提取数据。本篇文章将介绍另一个强大的解析工具:XPath。XPath是一种在XML文档中查找信息的语言,同样适用于HTML文档。它的语法简洁而强大,特别适合处理结构复杂的网…...

二分小专题
P1102 A-B 数对 P1102 A-B 数对 暴力枚举还是很好做的,直接上双层循环OK 二分思路:查找边界情况,找出最大下标和最小下标,两者相减1即为答案所求 废话不多说,上代码 //暴力O(n^3) 72pts // #include<bits/stdc.h> // usin…...

Langchain检索YouTube字幕
创建一个简单搜索引擎,将用户原始问题传递该搜索系统 本文重点:获取保存文档——保存向量数据库——加载向量数据库 专注于youtube的字幕,利用youtube的公开接口,获取元数据 pip install youtube-transscript-api pytube 初始化 …...
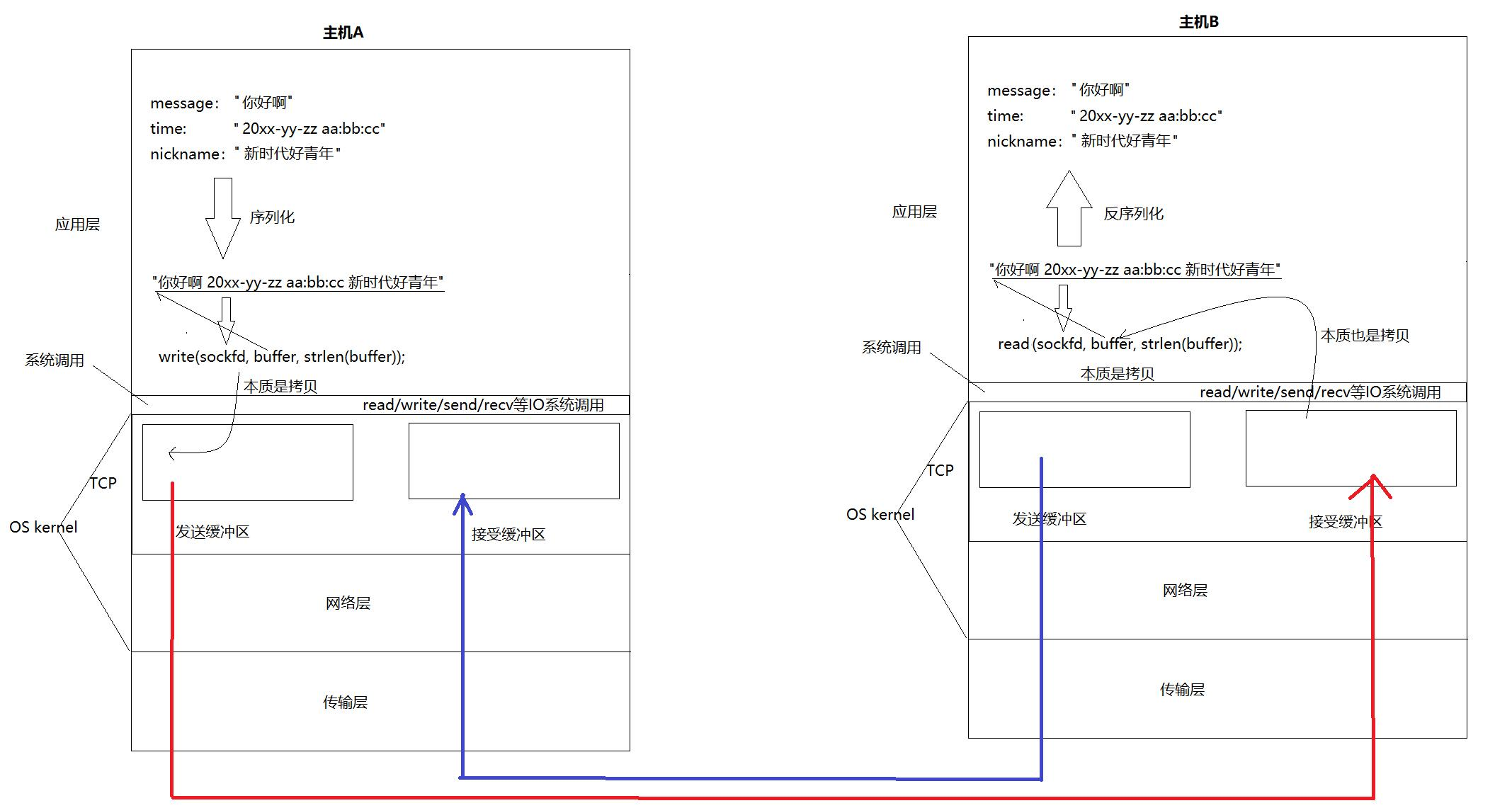
【Linux网络】应用层自定义协议与序列化及Socket模拟封装
📢博客主页:https://blog.csdn.net/2301_779549673 📢博客仓库:https://gitee.com/JohnKingW/linux_test/tree/master/lesson 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正! &…...

客户案例:西范优选通过日事清实现流程与项目管理的优化
近几年来,新零售行业返璞归真,从线上销售重返线下发展,满足消费者更加多元化的需求,国内家居集合店如井喷式崛起。为在激烈的市场竞争中立于不败之地,西范优选专注于加强管理能力、优化协作效率的“内功修炼”…...

LabVIEW实现Voronoi图绘制功能
该 LabVIEW 虚拟仪器(VI)借助 MathScript 节点,实现基于手机信号塔位置计算 Voronoi 图的功能。通过操作演示,能直观展示 Voronoi 图在空间划分上的应用。 各部分功能详细说明 随机地形创建部分 功能:根据 “Maximum a…...
