1468-PIPI的魔咒
题目描述:
大魔术师PIPI有N个转换魔咒,每个转换魔咒可以将一个字符串变成另一个字符串。
比如说:
“PIPI”->“POPO”
“boy”->“girl”
“boy”->“u”
“isau”->“OJ”
那么对于字符串"PIPIisaboy",大魔术师PIPI可以通过2次魔咒将"PIPIisaboy"变成"POPOisagirl"。
也可以通过2次魔咒将"PIPIisaboy"变成"PIPIOJ"。
现在你知道了PIPI的所有魔咒,想让他把字符串A变成字符串B,请输出变换所需的最少步数。
输入:
输入包含单组测试样例。
第一行输入字符串A和字符串B。1≤|A|,|B|≤30。
接下来输入一个数字N,代表转换魔咒的个数(1≤N≤10)。
接下来N行,每一行输入一个转换规则 X Y,代表可以将字符串X转化为Y。 1≤|X|,|Y|≤30。
本题给出的所有字符串均不包含空格。
输出:
如果在10次之内能将A变为B,输出从字符串A变为字符串B的最少次数。否则输出-1。
样例输入:
PIPIisaboy POPOisagirl
4
PIPI POPO
boy girl
boy u
isau OJ
样例输出:
2
题解代码如下:
#include <bits/stdc++.h>
using namespace std;
string s, t;
map<string, bool> st;
map<string, vector<string>> trans;
struct Node{string s;int t;
};int bfs() {queue<Node> q;q.push({s, 0});st[s] = true;while (q.size()) {auto now = q.front(); q.pop();if (now.t > 10) continue;if (now.s == t) {return now.t;}for (int L = 0; L < now.s.size(); L++) {for (int len = 1; L + len - 1 < now.s.size(); len++) {string subs = now.s.substr(L, len);if (trans.count(subs)) {for (int i = 0; i < trans[subs].size(); i++) {string ns = now.s;ns.replace(L, len, trans[subs][i]);if (!st[ns]) {st[ns] = true;q.push({ns, now.t + 1});}}}}}}return -1;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> s >> t;int n;cin >> n;while (n--) {string a, b;cin >> a >> b;trans[a].push_back(b);}cout << bfs() << endl;return 0;
}
相关文章:

1468-PIPI的魔咒
题目描述: 大魔术师PIPI有N个转换魔咒,每个转换魔咒可以将一个字符串变成另一个字符串。 比如说: “PIPI”->“POPO” “boy”->“girl” “boy”->“u” “isau”->“OJ” 那么对于字符串"PIPIisaboy",大魔术师PIPI可…...
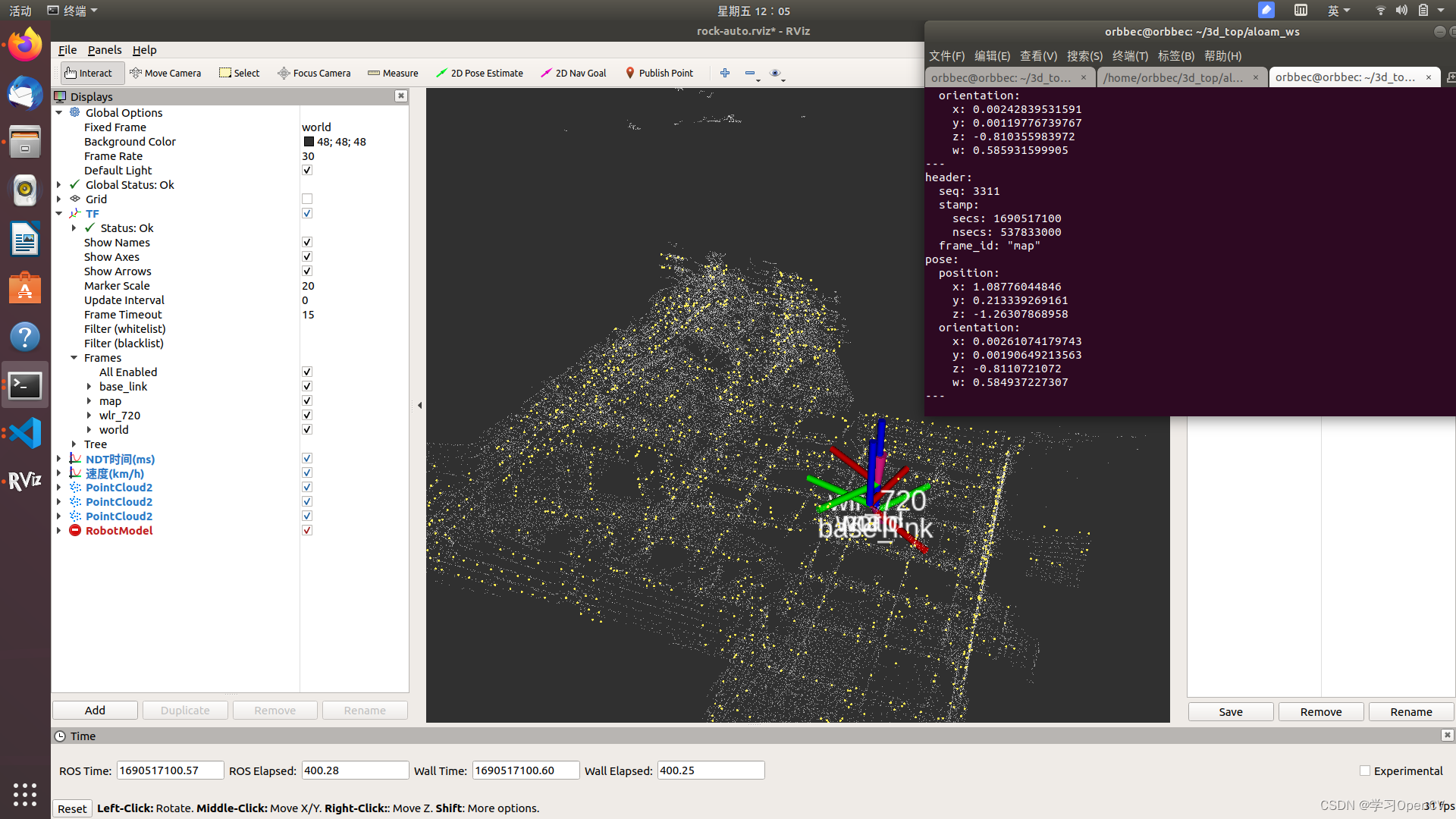
3d激光slam建图与定位(1)_基于ndt算法定位
一.代码实现流程 二.ndt算法原理 一.该算法定位有三个进程文件 1.map_loader.cpp用于点云地图的读取,从文件中读取点云后对这个点云地图进行旋转平移后发布点云地图到ros #include "map_loader.h"MapLoader::MapLoader(ros::NodeHandle &nh){std::st…...
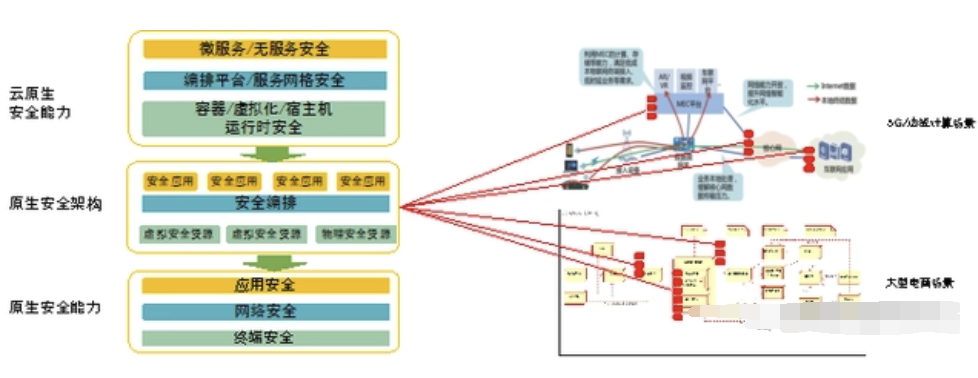
云安全攻防(二)之 云原生安全
云原生安全 什么是云原生安全?云原生安全包含两层含义:面向云原生环境的安全和具有云原生特征的安全 面向云原生环境的安全 面向云原生环境的安全的目标是防护云原生环境中的基础设施、编排系统和微服务系统的安全。这类安全机制不一定会具有云原生的…...
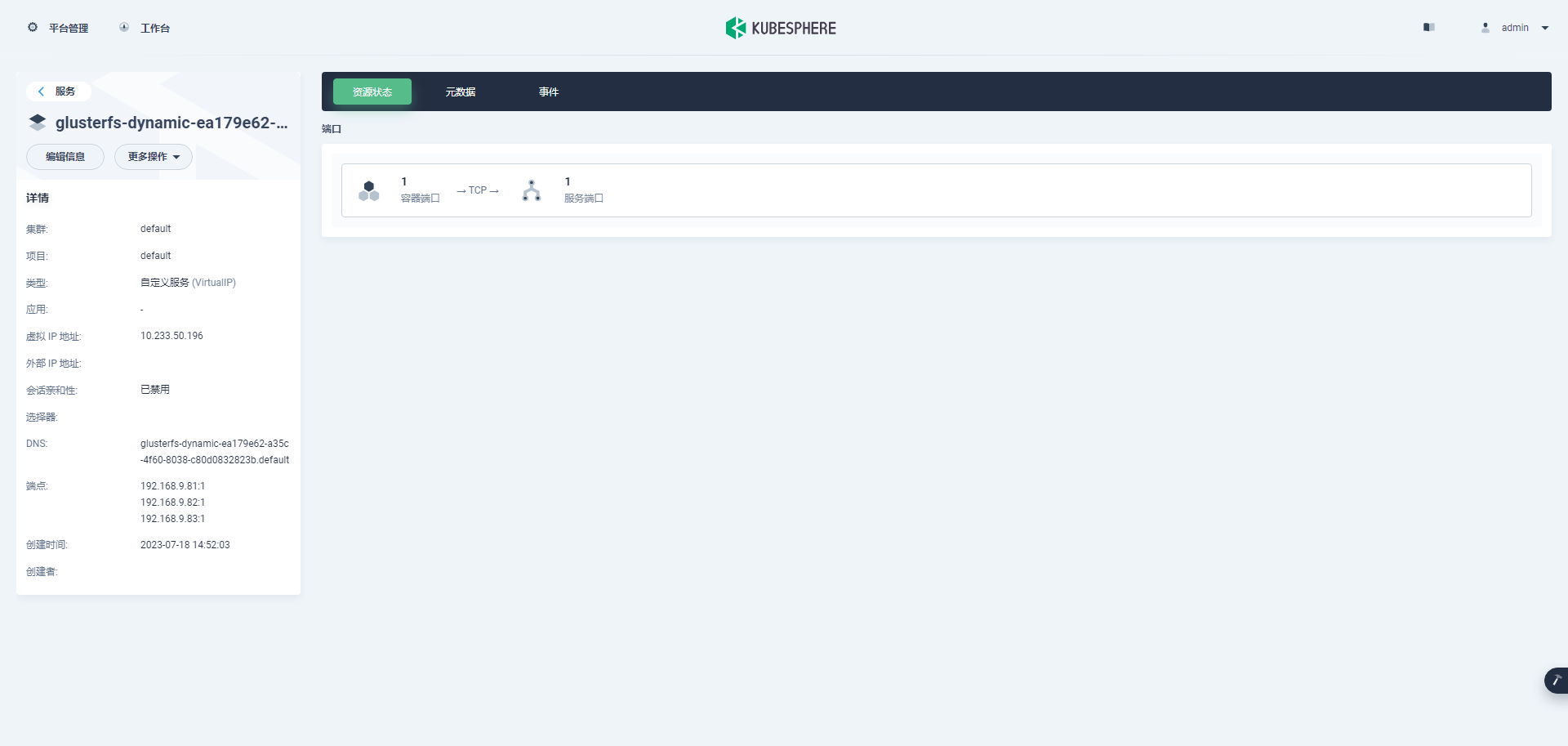
最后的组合:K8s 1.24 基于 Hekiti 实现 GlusterFS 动态存储管理实践
前言 知识点 定级:入门级GlusterFS 和 Heketi 简介GlusterFS 安装部署Heketi 安装部署Kubernetes 命令行对接 GlusterFS 实战服务器配置(架构 1:1 复刻小规模生产环境,配置略有不同) 主机名IPCPU内存系统盘数据盘用途ks-master-0192.168.9.912450100…...
)
笙默考试管理系统-MyExamTest(16)
笙默考试管理系统-MyExamTest(16) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试管理系统-MyExa…...

初级算法-树
文章目录 二叉树的最大深度题意:解:代码: 验证二叉搜索树题意:解:代码: 对称二叉树题意:解:代码: 二叉树的层序遍历题意:解:代码: 将有…...

Harbor Failed to start docker.service: Unit docker.service not found.
有可能是修改配置文件导致了问题,最近肯定修改过某个配置文件 本文只针对配置Harbor过程中遇到该问题,很有是deamon.json的 insecure-registries和docker.service的 ExecStart/usr/bin/dockerd --insecure-registry冲突了,删掉一个就好 我使…...
网络安全/信息安全(黑客技术)自学笔记
一、网络安全基础知识 1.计算机基础知识 了解了计算机的硬件、软件、操作系统和网络结构等基础知识,可以帮助您更好地理解网络安全的概念和技术。 2.网络基础知识 了解了网络的结构、协议、服务和安全问题,可以帮助您更好地解决网络安全的原理和技术…...
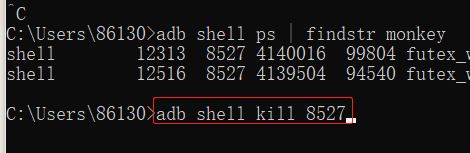
ADB 命令结合 monkey 的简单使用,超详细
一:ADB简介 1,什么是adb: ADB 全称为 Android Debug Bridge,起到调试桥的作用,是一个客户端-服务器端程序。其中客户端是用来操作的电脑,服务端是 Android 设备。ADB 也是 Android SDK 中的一个工具&…...
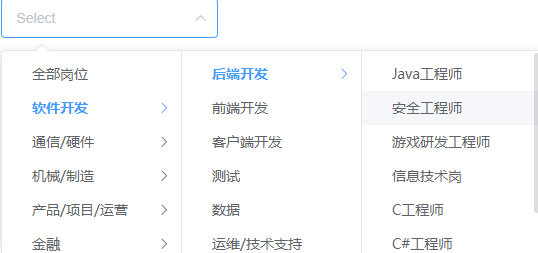
级联选择框
文章目录 实现级联选择框效果图实现前端工具版本添加依赖main.js导入依赖级联选择框样式 后端数据库设计 实现级联选择框 效果图 实现 前端 工具版本 node.js v16.6.0vue3 级联选择框使用 Element-Plus 实现 添加依赖 在 package.json 添加依赖,并 npm i 导入…...
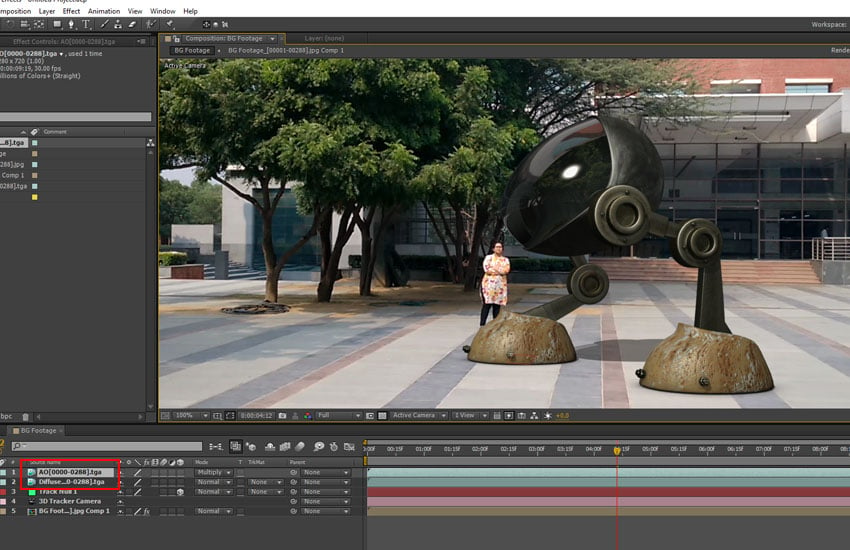
如何在3ds max中创建可用于真人场景的巨型机器人:第 5 部分
推荐: NSDT场景编辑器助你快速搭建可二次开发的3D应用场景 1. After Effects 中的项目设置 步骤 1 打开“后效”。 打开后效果 步骤 2 我有真人版 我在After Effects中导入的素材。这是将 用作与机器人动画合成的背景素材。 实景镜头 步骤 3 有背景 选定的素材…...
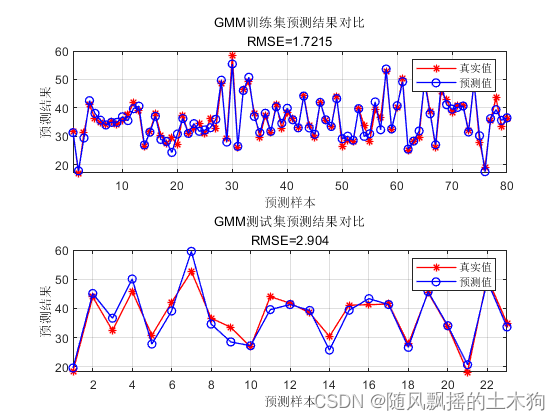
【MATLAB第61期】基于MATLAB的GMM高斯混合模型回归数据预测
【MATLAB第61期】基于MATLAB的GMM高斯混合模型回归数据预测 高斯混合模型GMM广泛应用于数据挖掘、模式识别、机器学习和统计分析。其中,它们的参数通常由最大似然和EM算法确定。关键思想是使用高斯混合模型对数据(包括输入和输出)的联合概率…...
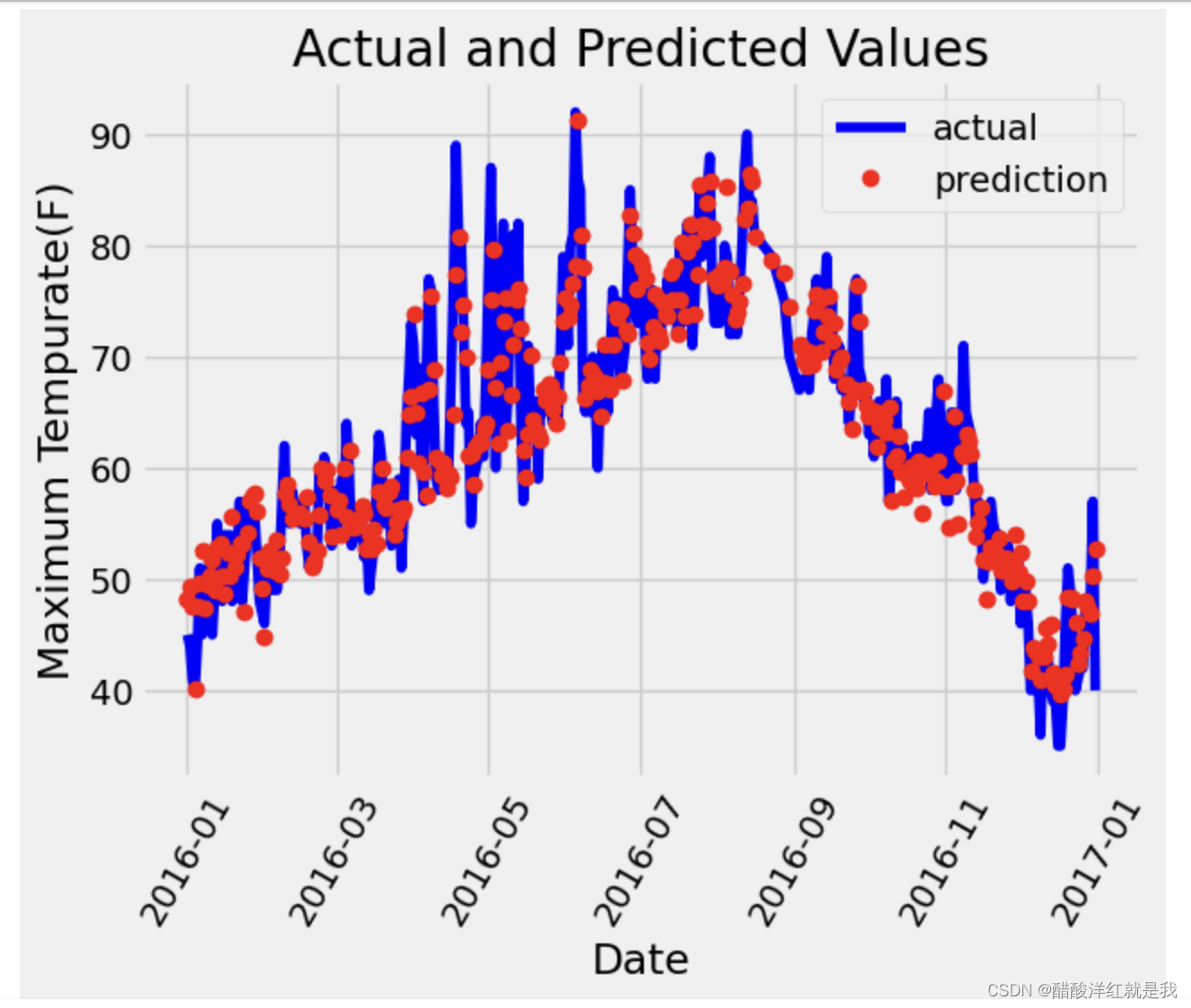
Mnist分类与气温预测任务
目录 传统机器学习与深度学习的特征工程特征向量pytorch实现minist代码解析归一化损失函数计算图Mnist分类获取Mnist数据集,预处理,输出一张图像面向工具包编程使用TensorDataset和DataLoader来简化数据预处理计算验证集准确率 气温预测回归构建神经网络…...

Pytorch深度学习-----神经网络的卷积操作
系列文章目录 PyTorch深度学习——Anaconda和PyTorch安装 Pytorch深度学习-----数据模块Dataset类 Pytorch深度学习------TensorBoard的使用 Pytorch深度学习------Torchvision中Transforms的使用(ToTensor,Normalize,Resize ,Co…...

微信小程序转抖音小程序的坑:The component <xxx> used in pages/xxx/xxx is undefined
微信小程序组件定义在根目录的 app.json 中了,在抖音小程序中出现找不到的情况。 在需要用到组件的 pages 目录中页面文件夹的 json "usingComponents": {} 大括号中添加页面使用的组件,即可使用......

Vue+element Ui的el-select同时获取value和label的方法总结
1.通过ref的形式(推荐) <template><div class"root"><el-selectref"optionRef"change"handleChange"v-model"value"placeholder"请选择"style"width: 250px"><el-optionv-for&q…...
乐划锁屏充分发挥强创新能力,打造内容业新生态
乐划锁屏作为新型内容媒体,在这一市场有着众多独特的优势,不仅能够通过多场景的联动给内容创作者带来了更多可能性,还促进了更多优质作品的诞生,为用户带来更加丰富多彩的锁屏使用体验。 作为OPPO系统原生的OS应用,乐划锁屏一直致力于打造为用户提供至美内容的内容平台,吸引了全…...

防御第三天
1.总结当堂NAT与双机热备原理,形成思维导图 2.完成课堂NAT与双机热备实验 fw1: <USG6000V1>sy [USG6000V1]int g0/0/0 [USG6000V1-GigabitEthernet0/0/0]ip add 192.168.18.2 24 [USG6000V1-GigabitEthernet0/0/0]service-manage all permit (地址无所谓&…...

用JavaScript和HTML实现一个精美的计算器
文章目录 一、前言二、技术栈三、功能实现3.1 引入样式3.2 编写显示页面3.2 美化计算器页面3.3 实现计算器逻辑 四、总结 一、前言 计算器是我们日常生活中经常使用的工具之一,可以帮助我们进行简单的数学运算。在本博文中,我将使用JavaScript编写一个漂…...
地址省市区解析函数)
基于postgresl的gaussDB(DWS)地址省市区解析函数
地址格式为: 省(自治区,直辖市)、市、区。 直辖市的地址格式为, 北京市北京市海淀区xxxxx。 若是北京市海淀区xxx,自己改改就可以了 采用的是笨办法,穷举。 涉及的两个主要内置函数。 1. instr( <start_positio…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
