2023.7.26(同余方程的通解与特解)
Water(扩欧求特解与通解)
题意:给容量分别为A与B的水杯,问确切喝到C水的最小操作次数
有4种操作:选一杯全喝,选一杯全部倒掉,选一杯装满,将一杯的水尽量倒到另一杯中
思路:只有Ax+By=C有解时才能确切喝到X水
裴蜀定理:如果a、b是整数,那么一定存在整数x、y使得ax+by=k*gcd(a,b)。
思路:要求x,y的特解,可以使用exgcd的板子,令c = k * gcd(A, B)则Ax + By = c;exgcd求出来的是k = 1时的特解
只要将x *= c / gcd(A, B), y *= c / gcd(A, B);此时x和y就是方程Ax + By = c的特解
这里有一个步长的概念对于x他的步长是 B / gcd(A, B), 对于y他的步长是 A / gcd(A, B)
要求最小整数解,只需要把x除上他的步长就能知道x要走多少步才能最接近0,再把x -= 步长 * 步数就可以让x最接近0,然
后在对原点附近的 (x+t⋅步长,y−t⋅步长)求min即可得到最小整数解
#include<bits/stdc++.h>
using namespace std;#define endl '\n'
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
typedef pair<int, int> pr;#define int long long
#define ll long long
#define fr(i,l,r) for(int i=l;i<=r;i++)
#define ufr(i,n,z) for(int i = n;i >= z; i--)
#define pb(x) push_back(x)
#define all(a) a.begin(),a.end()
#define fi first
#define se secondconst int N = 1e6 + 10;
const int mod = 998244353, inf = LONG_LONG_MAX;
int dx[] = { 0,0,-1,0,1 }, dy[] = { 0,-1,0,1,0 };
int n, m;int a[N];
int gcd(int a, int b) { //辗转相除return !b ? a : gcd(b, a % b);
}
int exgcd(int a, int b, int& x, int& y) //扩欧板子
{if (b == 0) {x = 1; y = 0;return a; //到达递归边界开始向上一层返回}ll d = exgcd(b, a % b, y, x);y -= (a / b) * x;return d;
}
void solve()
{int a, b, c;cin >> a >> b >> c;if (c % gcd(a, b) != 0) {cout << -1 << '\n'; //无解}else {int x, y;int d = exgcd(a, b, x, y);x *= c / d; y *= c / d; //特解(除去最大公约数乘上C)int dx = b / d; int dy = a / d;y += (x / dx) * dy;x -= (x / dx) * dx; //最小整数解,只需要把x除上他的步长就能知道x要走多少步才能最接近0int ans = inf;fr(i, -10, 10) {int xx = x + dx * i; int yy = y - dy * i; //通解ans = min(ans, max((xx + yy) << 1, (abs(xx - yy) << 1) - 1));}cout << ans << '\n';}
}signed main()
{// ios;int t = 1;cin >> t;while (t--) solve();return 0;
}
P1082 [NOIP2012 提高组] 同余方程
题意:求ax->1(mod b)的最小整数解,输入数据保证一定有解。
转变为ax=1+by,移项ax-by=1,
扩欧求的特解x/d,y/d,
通解x/d-i*(x/d/b/d)*b/d->x/d-x/b*(b/d)->x/d-i*x/d
#include<iostream>
#define int long long
using namespace std;
int exgcd(int a, int b, int& x, int& y) {if (b == 0) {x = 1, y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= (a / b) * x;return d;
}
signed main(){int a, b;int x, y;cin >> a >> b;exgcd(a, b, x, y);cout << (x % b + b) % b << '\n';return 0;
}相关文章:
)
2023.7.26(同余方程的通解与特解)
Water(扩欧求特解与通解) 题意:给容量分别为A与B的水杯,问确切喝到C水的最小操作次数 有4种操作:选一杯全喝,选一杯全部倒掉,选一杯装满,将一杯的水尽量倒到另一杯中 思路:只有AxByC有解时才能确…...

Diffusion扩散模型学习3——Stable Diffusion结构解析-以图像生成图像(图生图,img2img)为例
Diffusion扩散模型学习3——Stable Diffusion结构解析-以图像生成图像(图生图,img2img)为例 学习前言源码下载地址网络构建一、什么是Stable Diffusion(SD)二、Stable Diffusion的组成三、img2img生成流程1、输入图片编…...

LangChain||什么是LangChain? LangChain有什么用?
从Auto-GPT说起: Auto-GPT可以调用本地电脑工具处理复杂信息;Auto-GPT可以围绕目标查阅资 料、“独立思考”、及时反馈、并 及时调整下一步操作…Auto-GPT的诞生,创造了大家 对“将LLM作为智慧大脑来高效 处理综合复杂任务”的想象;首次尝试串联大语言模…...

秋招算法备战第28天 | 93.复原IP地址、78.子集、90.子集II
93. 复原 IP 地址 - 力扣(LeetCode) 这个问题可以通过深度优先搜索(DFS)的方法来解决。我们要做的就是在字符串的每个可能位置插入点,然后检查生成的每一部分是否在 0-255 的范围内,以及是否没有前导零(除非这一部分本…...

Mongodb空间索引的使用以及与Django的对接
Mongodb的空间索引 Mongodb数据库大家都非常熟悉,是一个基于分布式文件存储的开源数据库系统,在高负载的情况下,添加更多的节点,可以保证服务器性能,数据结构由键值(key>value)对组成。MongoDB 文档类似于 JSON 对…...

Windows安装MySQL数据库
MySQL数据库安装 MySQL下载 下载地址:https://dev.mysql.com/downloads/mysql/ 可以选择下载msi或zip,以下为zip模式安装步骤 下载了mysql的zip安装包之后解压即可; Windows安装步骤 初始化MySQL,并记录生成的用户密码root的随机…...

聊聊函数式编程中的“式”
当谈到函数式编程的“式”时,通常指的是函数的组合、转换和应用,以及处理数据的方式和风格。在函数式编程中,式是用来构建程序逻辑的基本单元。 下面更详细解释函数式编程中的几个关键式: 函数的组合: 函数式编程中…...

ubuntu目录分析
在Ubuntu根目录下,以下是一些常见文件夹的含义: /bin:存放可执行文件,包含一些基本的命令和工具。 /boot:存放启动时所需的文件,如内核和引导加载程序。 /dev:包含设备文件,用于与硬…...

Python 进阶(三):正则表达式(re 模块)
❤️ 博客主页:水滴技术 🌸 订阅专栏:Python 入门核心技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 文章目录 1. 导入re模块2. re模块中的常用函数2.1 re.search()2.2 re.findall()2.3 re.sub()2.4…...
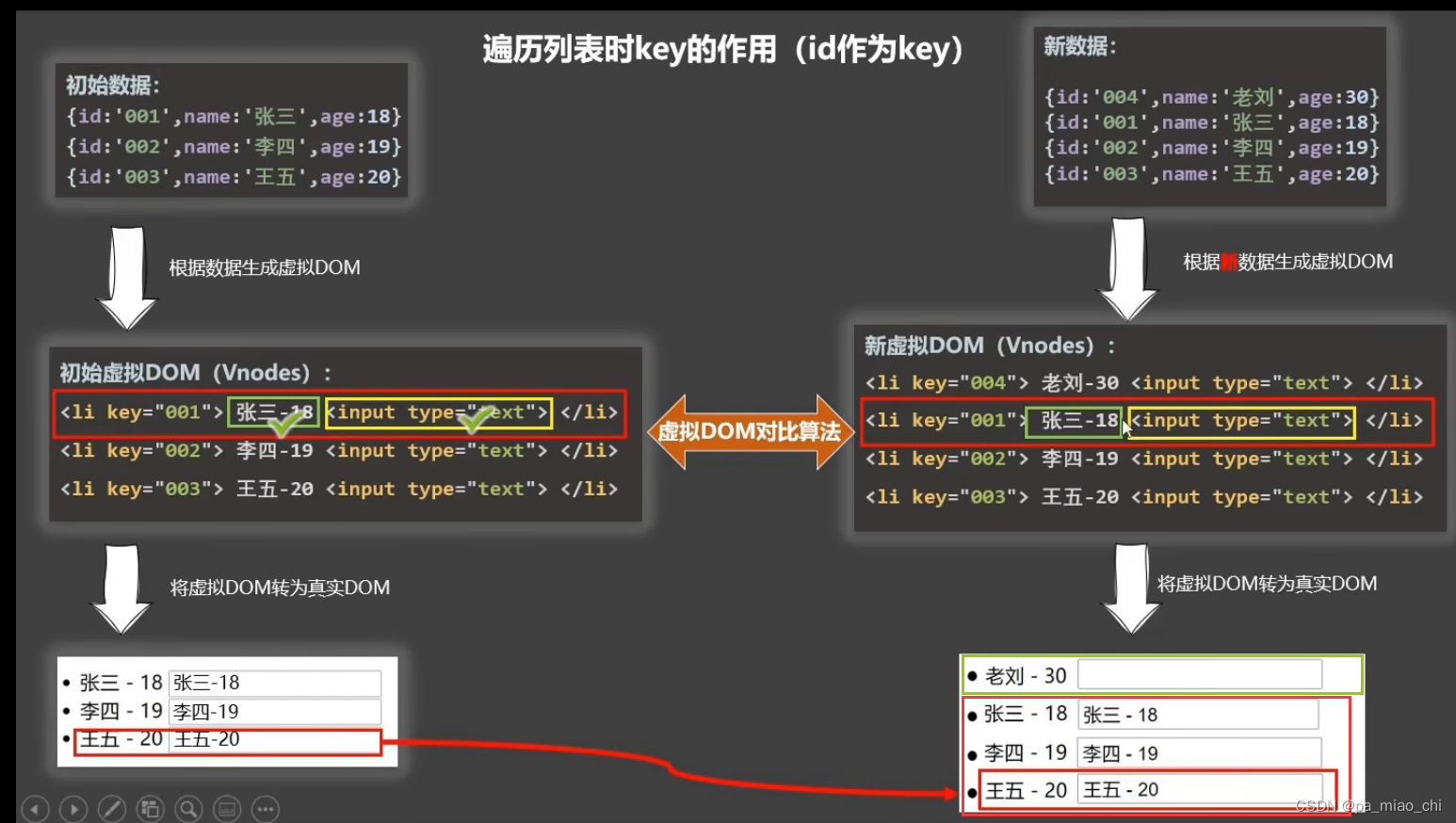
Vue2 第六节 key的作用与原理
(1)虚拟DOM (2)v-for中的key的作用 一.虚拟DOM 1.虚拟DOM就是内存中的数据 2.原生的JS没有虚拟DOM: 如果新的数据和原来的数据有重复数据,不会在原来的基础上新加数据,而是重新生成一份 3. Vue会有虚拟…...

React之组件的生命周期
React之组件的生命周期 一、概述二、整体说明三、挂载阶段四、更新阶段五、卸载阶段 一、概述 生命周期:一个事务从创建到最后消亡经历的整个过程组件的生命周期:组件从被创建到挂载到页面中运行,再到组件不用时卸载的过程意义:理解组件的生…...

linux -网络编程-多线程并发服务器
目录 1.三次握手和四次挥手 2 滑动窗口 3 函数封装思想 4 高并发服务器 学习目标: 掌握三次握手建立连接过程掌握四次握手关闭连接的过程掌握滑动窗口的概念掌握错误处理函数封装实现多进程并发服务器实现多线程并发服务器 1.三次握手和四次挥手 思考: 为什么…...

Golang之路---02 基础语法——字典
字典 字典(Map 类型),是由若干个 key:value 这样的键值对映射组合在一起的数据结构。 key 不能是切片,不能是字典,不能是函数。 字典初始化 方式:map[KEY_TYPE]VALUE_TYPE //1.var map1 map[string]int…...
)
Pytorch(三)
一、经典网络架构图像分类模型 数据预处理部分: 数据增强数据预处理DataLoader模块直接读取batch数据 网络模块设置: 加载预训练模型,torchvision中有很多经典网络架构,可以直接调用注意别人训练好的任务跟咱们的并不完全一样,需要把最后…...
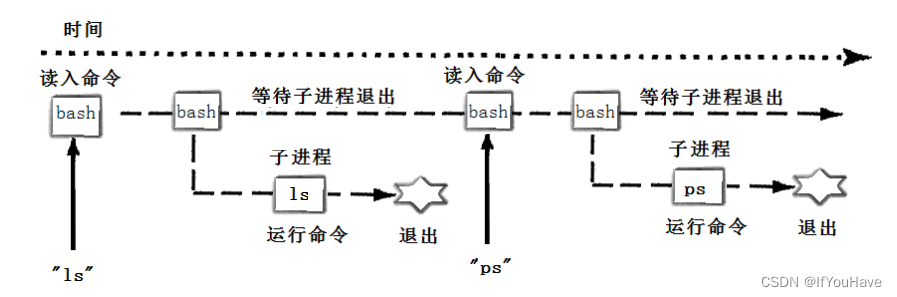
Linux——进程控制
目录 1. 进程创建 1.1 fork函数 1.2 fork系统调用内部宏观流程 1.3 fork后子进程执行位置分析 1.4 fork后共享代码分析 1.5 fork返回值 1.6 写时拷贝 1.7 fork常规用法 1.8 fork调用失败的原因 2.进程终止 2.1 进程退出场景 2.2 strerror函数—返回描述错误号的字符…...
)
剑指 Offer 59 - I. 滑动窗口的最大值 / LeetCode 239. 滑动窗口最大值(优先队列 / 单调队列)
题目: 链接:剑指 Offer 59 - I. 滑动窗口的最大值;LeetCode 239. 滑动窗口最大值 难度:困难 下一篇:剑指 Offer 59 - II. 队列的最大值(单调队列) 给你一个整数数组 nums,有一个大…...
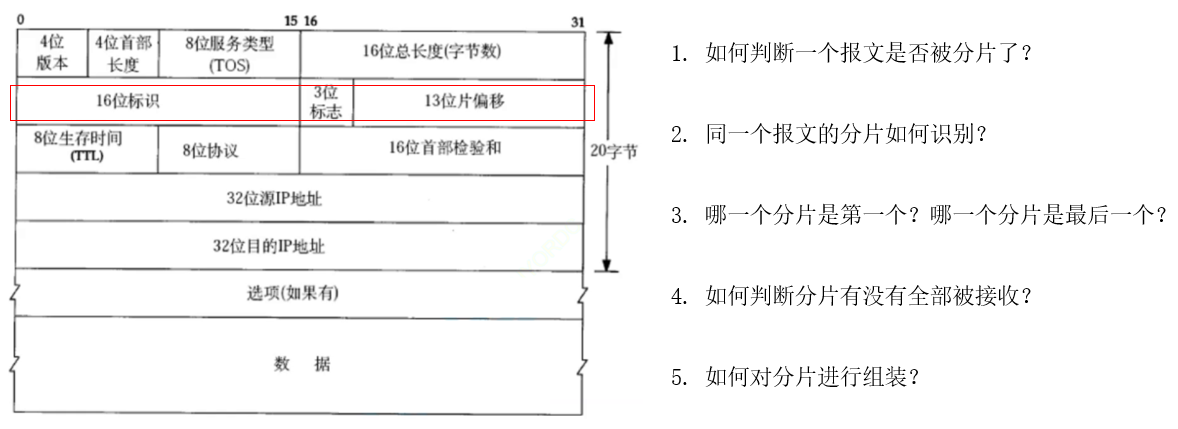
【Linux后端服务器开发】IP协议
目录 一、IP协议概述 二、协议头格式 三、网段划分 四、IP地址的数量限制 五、路由 六、分片和组装 一、IP协议概述 主机:配有IP地址,但是不进行路由控制的设备 路由器:即配有IP地址,又能进行路由控制 节点:主…...

React组件进阶之children属性,props校验与默认值以及静态属性static
React组件进阶之children属性,props校验与默认值以及静态属性static 一、children属性二、props校验2.1 props说明2.2 prop-types的安装2.3 props校验规则2.4 props默认值 三、静态属性static 一、children属性 children 属性:表示该组件的子节点,只要组…...
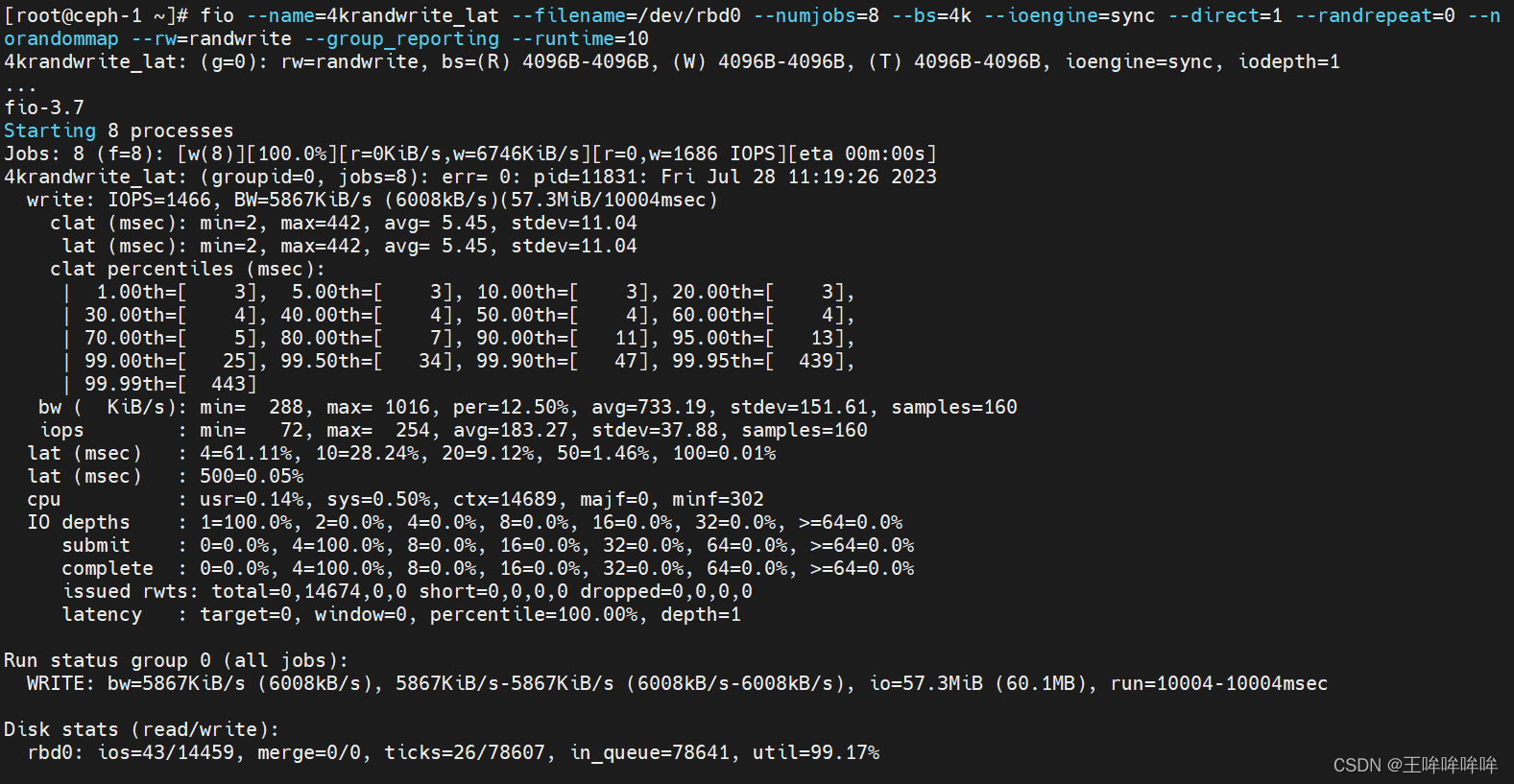
ceph集群中RBD的性能测试、性能调优
文章目录 rados benchrbd bench-write测试工具Fio测试ceph rbd块设备的iops性能测试ceph rbd块设备的带宽测试ceph rbd块设备的延迟 性能调优 rados bench 参考:https://blog.csdn.net/Micha_Lu/article/details/126490260 rados bench为ceph自带的基准测试工具&am…...

texshop mac中文版-TeXShop for Mac(Latex编辑预览工具)
texshop for mac是一款可以在苹果电脑MAC OS平台上使用的非常不错的Mac应用软件,texshop for mac是一个非常有用的工具,广泛使用在数学,计算机科学,物理学,经济学等领域的合作,这些程序的标准tetex分布特产…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
