对顶堆算法
对顶堆可以动态维护一个序列上的第k大的数,由一个大根堆和一个小根堆组成,
- 小根堆维护前k大的数(包含第k个)
- 大根堆维护比第k个数小的数
[CSP-J2020] 直播获奖
题目描述
NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩,并直播即时的获奖分数线。本次竞赛的获奖率为 w % w\% w%,即当前排名前 w % w\% w% 的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了 p p p 个选手的成绩,则当前计划获奖人数为 max ( 1 , ⌊ p × w % ⌋ ) \max(1, \lfloor p \times w \%\rfloor) max(1,⌊p×w%⌋),其中 w w w 是获奖百分比, ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ 表示对 x x x 向下取整, max ( x , y ) \max(x,y) max(x,y) 表示 x x x 和 y y y 中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮 CCF 写一个直播程序。
输入格式
第一行有两个整数 n , w n, w n,w。分别代表选手总数与获奖率。
第二行有 n n n 个整数,依次代表逐一评出的选手成绩。
输出格式
只有一行,包含 n n n 个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
样例 #1
样例输入 #1
10 60
200 300 400 500 600 600 0 300 200 100
样例输出 #1
200 300 400 400 400 500 400 400 300 300
样例 #2
样例输入 #2
10 30
100 100 600 100 100 100 100 100 100 100
样例输出 #2
100 100 600 600 600 600 100 100 100 100
提示
样例 1 解释
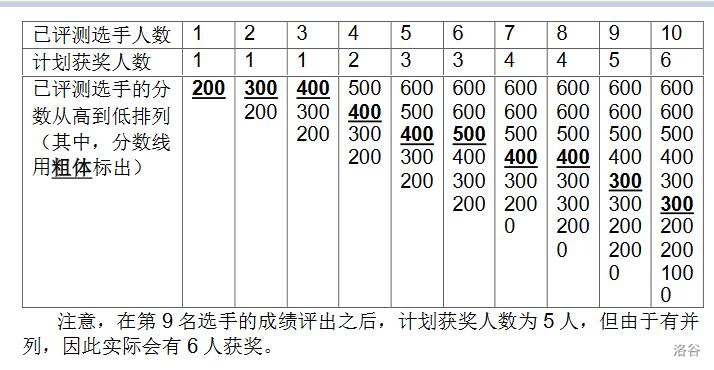
数据规模与约定
各测试点的 n n n 如下表:
| 测试点编号 | n = n= n= |
|---|---|
| 1 ∼ 3 1 \sim 3 1∼3 | 10 10 10 |
| 4 ∼ 6 4 \sim 6 4∼6 | 500 500 500 |
| 7 ∼ 10 7 \sim 10 7∼10 | 2000 2000 2000 |
| 11 ∼ 17 11 \sim 17 11∼17 | 1 0 4 10^4 104 |
| 18 ∼ 20 18 \sim 20 18∼20 | 1 0 5 10^5 105 |
对于所有测试点,每个选手的成绩均为不超过 600 600 600 的非负整数,获奖百分比 w w w 是一个正整数且 1 ≤ w ≤ 99 1 \le w \le 99 1≤w≤99。
提示
在计算计划获奖人数时,如用浮点类型的变量(如 C/C++ 中的 float 、 double,Pascal 中的 real 、 double 、 extended 等)存储获奖比例 w % w\% w%,则计算 5 × 60 % 5 \times 60\% 5×60% 时的结果可能为 3.000001 3.000001 3.000001,也可能为 2.999999 2.999999 2.999999,向下取整后的结果不确定。因此,建议仅使用整型变量,以计算出准确值。
思路
模版题: k为i*w/100
- 使用一个大根堆x维护比第k个数小的数
- 使用一个小根堆y来维护前k大的数
代码
#include <bits/stdc++.h>#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;void solve() {int n, w;cin >> n >> w;priority_queue<int> x;//大根堆 ,维护 ai<qpriority_queue<int, vector<int>, greater<>> y;//小根堆,维护ai>=q;for (int i = 1; i <= n; i++) {int a;cin >> a;if (y.empty() || a >= y.top()) y.push(a);else x.push(a);int k = max((int) 1, i * w / 100);while (y.size() > k) x.push(y.top()), y.pop();//保持小根堆有k个元素while (y.size() < k) y.push(x.top()), x.pop();cout << y.top() << " ";}
}signed main() {IOS
#ifndef ONLINE_JUDGEfreopen("../test.in", "r", stdin);freopen("../test.out", "w", stdout);
#endifint _ = 1;while (_--) solve();return 0;
}
[ABC306E] Best Performances
题面翻译
题目描述:
给定长度为 N N N 的数列 A = ( A 1 , A 2 , … , A N ) A=(A_1,A_2,\dots,A_N) A=(A1,A2,…,AN),最开始所有项均为 0 0 0。
定义函数 f ( A ) f(A) f(A) 如下:
将 A A A 按照降序(即使得 A A A 为广义单调递减序列)排序得到 B B B。
则 f ( A ) = B 1 + B 2 + ⋯ + B K f(A)=B_1+B_2+\dots+B_K f(A)=B1+B2+⋯+BK,其中 B B B 为排序后的数列, K K K 为 A A A 中不为 0 0 0 的元素个数。
现在对该数列进行 Q Q Q 次更新。对于每次更新,按顺序执行以下操作,并输出此时的 f ( A ) f(A) f(A) 值:
将 A X i A_{X_i} AXi 更改为 Y i Y_i Yi。
题目描述
样例 #1
样例输入 #1
4 2 10
1 5
2 1
3 3
4 2
2 10
1 0
4 0
3 1
2 0
3 0
样例输出 #1
5
6
8
8
15
13
13
11
1
0
提示
- $ 1\ \le\ K\ \le\ N\ \le\ 5\ \times\ 10^5 $
- $ 1\ \le\ Q\ \le\ 5\ \times\ 10^5 $
- $ 1\ \le\ X_i\ \le\ N $
- $ 0\ \le\ Y_i\ \le\ 10^9 $
思路
可以使用对顶堆,这里涉及到修改操作,因此可以使用multiset维护方便一些
- a维护前k大为小根堆
- b维护比第k个数小的,大根堆
使用res来维护前k大的和。
代码
#include <bits/stdc++.h>#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;const int N = 5e5 + 10;
int n, k, q, res;
int w[N];
multiset<int> a, b;//a维护前k大,小根堆 b维护比第k个数小的,大根堆
void solve() {cin >> n >> k >> q;for (int i = 1; i <= k; i++)a.insert(0);for (int i = 1; i <= n - k; i++) b.insert(0);while (q--) {int x, y;cin >> x >> y;if (a.find(w[x]) != a.end()) a.erase(a.find(w[x])), res -= w[x];else b.erase(b.find(w[x]));w[x] = y;if (!b.empty() && y >= *b.rbegin()) a.insert(y), res += y;else b.insert(y);while (a.size() > k) {b.insert(*a.begin());res -= *a.begin();a.erase(a.begin());}while (a.size() < k) {a.insert(*b.rbegin());res += *b.rbegin();b.erase(b.find(*b.rbegin()));}cout << res << endl;}
}signed main() {IOS
#ifndef ONLINE_JUDGEfreopen("../test.in", "r", stdin);freopen("../test.out", "w", stdout);
#endifint _ = 1;while (_--) solve();return 0;
}
相关文章:

对顶堆算法
对顶堆可以动态维护一个序列上的第k大的数,由一个大根堆和一个小根堆组成, 小根堆维护前k大的数(包含第k个)大根堆维护比第k个数小的数 [CSP-J2020] 直播获奖 题目描述 NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩&a…...

node.js的优点
提示:node.js的优点 文章目录 一、什么是node.js二、node.js的特性 一、什么是node.js 提示:什么是node.js? Node.js发布于2009年5月,由Ryan Dahl开发,是一个基于ChromeV8引擎的JavaScript运行环境,使用了一个事件驱…...

golang编译跨平台
golang可以在windows上编译出linux、MacOS等系统上的程序。 go编译器windows下可变翼linux程序,例如,GOARCHamd64 和 GOOSlinux 可以用于编译 64 位的 Linux 平台上的可执行文件。: set GOARCHamd64 set GOOSlinux go build main.go通过设置…...

关于Spring的bean的相关注解以及其简单使用方法
一、前置工作 第一步:创建一个maven项目 第二步:在resource中创建一个名字叫做spring-config.xml的文件,并把以下代码复制粘贴 <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.sprin…...

【计算机视觉】BLIP:源代码示例demo(含源代码)
文章目录 一、Image Captioning二、VQA三、Feature Extraction四、Image-Text Matching 一、Image Captioning 首先配置代码: import sys if google.colab in sys.modules:print(Running in Colab.)!pip3 install transformers4.15.0 timm0.4.12 fairscale0.4.4!g…...

TWILIGHT靶场详解
TWILIGHT靶场详解 下载地址:https://download.vulnhub.com/sunset/twilight.7z 这是一个比较简单的靶场,拿到IP后我们扫描发现开启了超级多的端口 其实这些端口一点用都没有,在我的方法中 但是也有不同的方法可以拿权限,就需要…...

【案例】--GPT衍生应用案例
目录 一、前言二、GPT实现智能问答架构2.1、基本的GPT实现智能问答架构2.2、可应用的GPT实现智能问答架构1、语义转换2、相似度关键字矩阵3、ES中搜索相似度关键字矩阵三、后续一、前言 GPT,全称Generative Pre-trained Transformer ,中文名可译作生成式预训练Transformer。…...

Sip网络音频对讲广播模块, sip网络寻呼话筒音频模块
Sip网络音频对讲广播模块, sip网络寻呼话筒音频模块 一、模块介绍 SV-2101VP和 SV-2103VP网络音频对讲广播模块 是一款通用的独立SIP音频功能模块,可以轻松地嵌入到OEM产品中。该模块对来自网络的SIP协议及RTP音频流进行编解码。 该模块支持多种网络协议…...
)
leetcode1219. 黄金矿工(java)
黄金矿工 leetcode1219. 黄金矿工题目描述回溯算法代码 回溯算法 leetcode1219. 黄金矿工 难度: 中等 eetcode 1219 黄金矿工 题目描述 你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元…...

Svelte框架入门
关键词 前端框架、编译器、响应式、模板 介绍 Svelte /svelt/ adj. 苗条的;线条清晰的;和蔼的 Svelte是一个前端组件框架,就像它的英文名字一样,Svelte的目标是打造一个更高性能的响应性前端框架。 Svelte类似于React和Vue框架&am…...
在linux中进行arm交叉编译体验tiny6410裸机程序开发流程
在某鱼上找了一个友善之臂的Tiny6410开发板用来体验一下嵌入式开发。这次先体验一下裸机程序的开发流程,由于这个开发板比较老旧了,官方文档有很多过期的内容,所以记录一下整个过程。 1. 交叉编译器安装 按照光盘A中的文档《04- Tiny6410 L…...
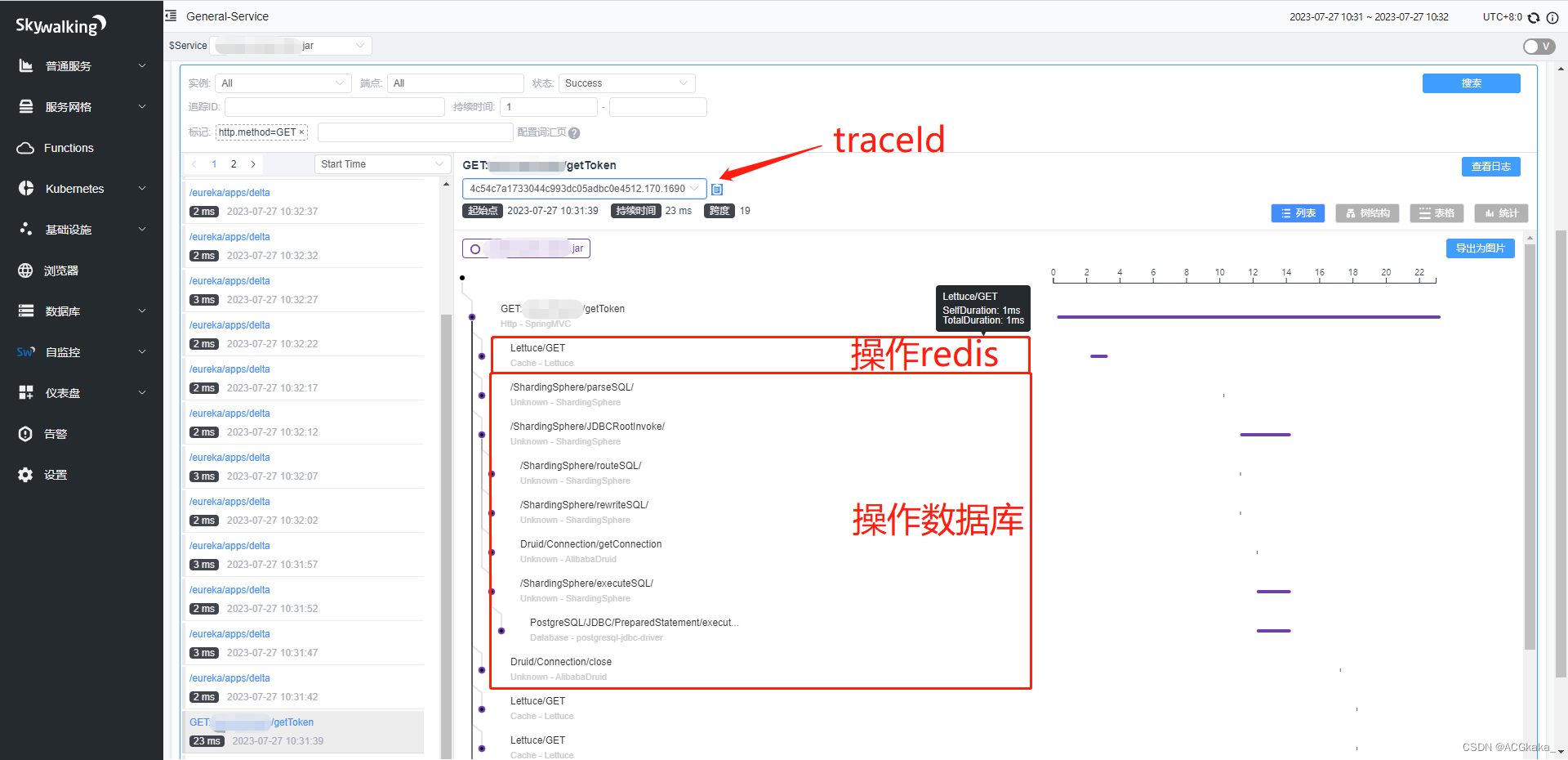
SpringBoot实战(二十三)集成 SkyWalking
目录 一、简介二、拉取镜像并部署1.拉取镜像2.运行skywalking-oap容器3.运行skywalking-ui容器4.访问页面 三、下载解压 agent1.下载2.解压 四、创建 skywalking-demo 项目1.Maven依赖2.application.yml3.DemoController.java 五、构建启动脚本1.startup.bat2.执行启动脚本3.发…...
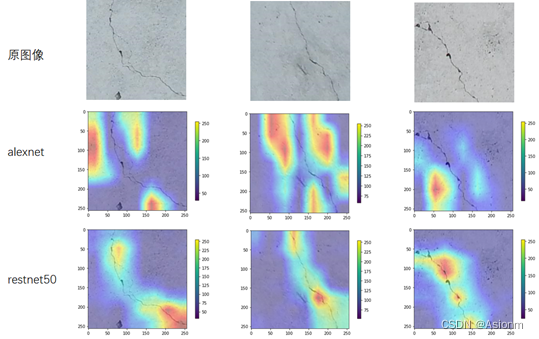
深度学习实践——卷积神经网络实践:裂缝识别
深度学习实践——卷积神经网络实践:裂缝识别 系列实验 深度学习实践——卷积神经网络实践:裂缝识别 深度学习实践——循环神经网络实践 深度学习实践——模型部署优化实践 深度学习实践——模型推理优化练习 深度学习实践——卷积神经网络实践ÿ…...
linux | vscode | makefile | c++编译和调试
简单介绍环境: vscode 、centos、 gcc、g、makefile 简单来说就是,写好项目然后再自己写makefile脚本实现编译。所以看这篇博客的用户需要了解gcc编译的一些常用命令以及makefile语法。在网上看了很多教程,以及官网也看了很多次,最…...

Spring | Bean 作用域和生命周期
一、通过一个案例来看 Bean 作用域的问题 Spring 是用来读取和存储 Bean,因此在 Spring 中 Bean 是最核心的操作资源,所以接下来我们深入学习⼀下 Bean 对象 假设现在有⼀个公共的 Bean,提供给 A 用户和 B 用户使用,然而在使用的…...
)
培训(c++题解)
题目描述 某培训机构的学员有如下信息: 姓名(字符串)年龄(周岁,整数)去年 NOIP 成绩(整数,且保证是 5 的倍数) 经过为期一年的培训,所有同学的成绩都有所提…...
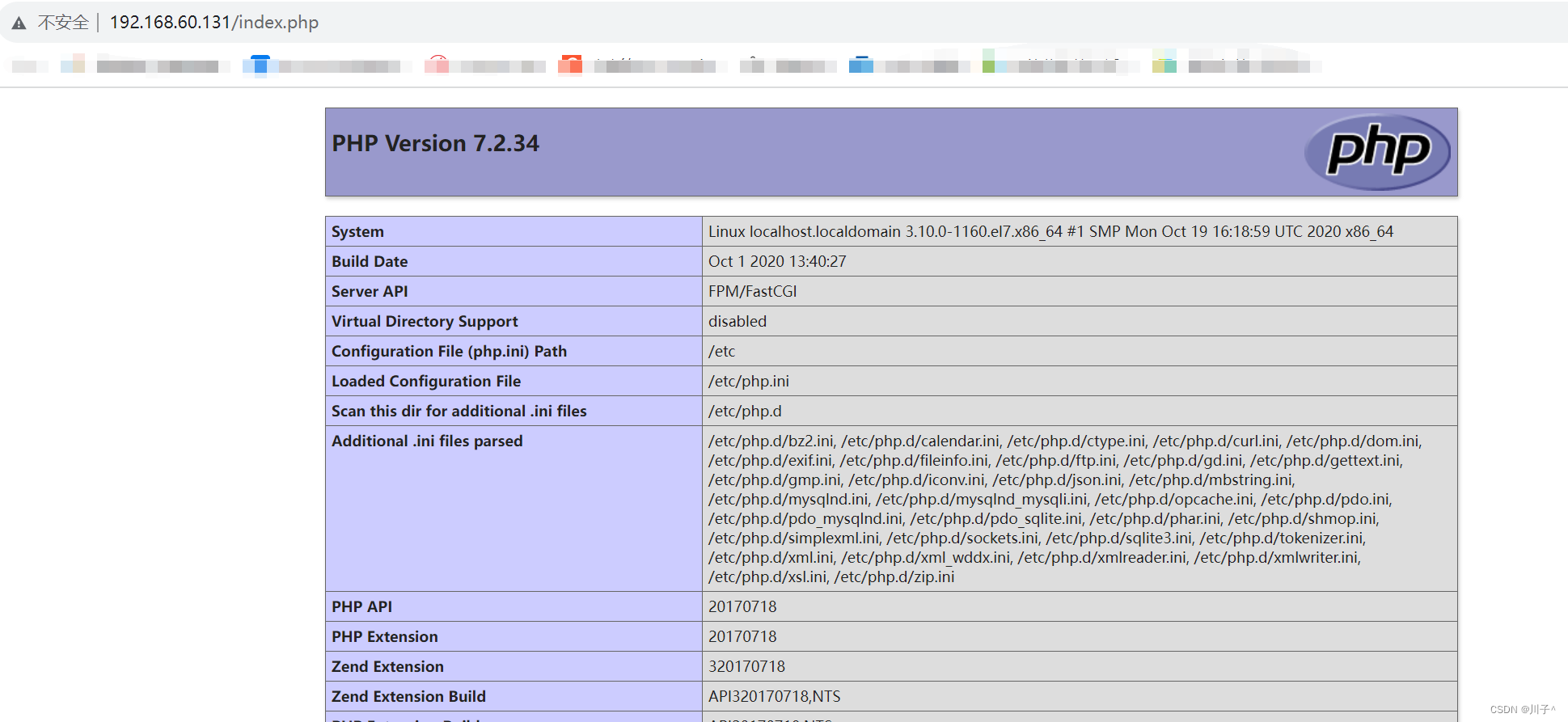
ansible-playbook编写 lnmp 剧本
ansible-playbook编写 lnmp 剧本 vim /opt/lnmp/lnmp.yaml执行剧本 ansible-playbook lnmp.yaml...

需求太多处理不过来?MoSCoW模型帮你
一、MoSCoW模型是什么 MoSCoW模型 是在项目管理、软件开发中使用的一种排序优先级的方法,以便开发人员、产品经理、客户对每个需求交付的重要性达成共识。 MoSCoW是一个首字母缩略词,代表: M(Must have):…...
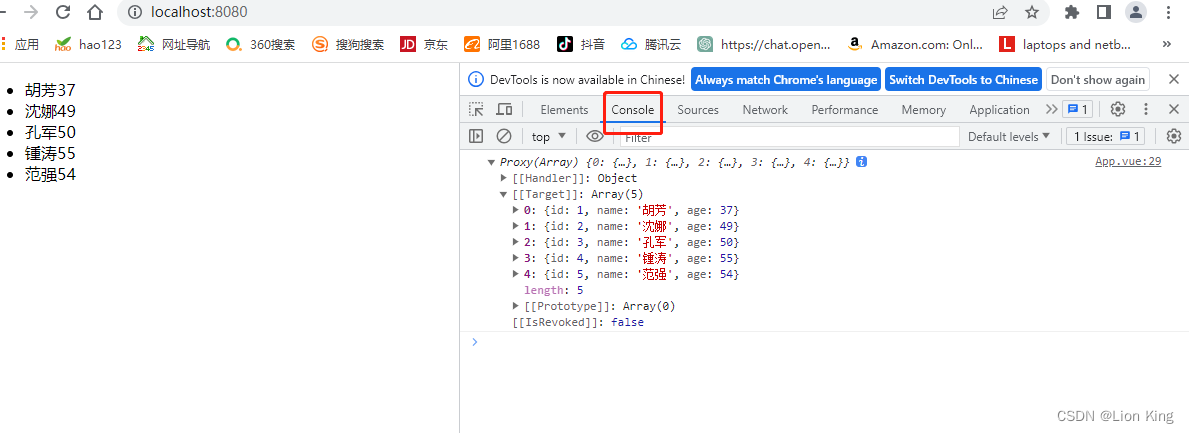
Vue 3:玩一下web前端技术(六)
前言 本章内容为VUE请求后端技术与相关技术讨论。 上一篇文章地址: Vue 3:玩一下web前端技术(五)_Lion King的博客-CSDN博客 下一篇文章地址: Vue 3:玩一下web前端技术(七)_Lio…...

【点云处理教程】00计算机视觉的Open3D简介
一、说明 Open3D 是一个开源库,使开发人员能够处理 3D 数据。它提供了一组用于 3D 数据处理、可视化和机器学习任务的工具。该库支持各种数据格式,例如 .ply、.obj、.stl 和 .xyz,并允许用户创建自定义数据结构并在程序中访问它们。 Open3D 广…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

