论文笔记--GloVe: Global Vectors for Word Representation
论文笔记--GloVe: Global Vectors for Word Representation
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 两种常用的单词向量训练方法
- 3.2 GloVe
- 3.3 模型的复杂度
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:GloVe: Global Vectors for Word Representation
- 作者:Jeffrey Pennington, Richard Socher, Christopher D. Manning
- 日期:2014
- 期刊:EMNLP
2. 文章概括
文章提出了一种新的单词表示的训练方法:Glove。该方法结合了基于统计方法和基于上下文窗口方法的优势,在多个下游任务上超越了当下SOTA方法的表现。
3 文章重点技术
3.1 两种常用的单词向量训练方法
现有的两类常用的单词向量训练方法为
- 基于矩阵分解的方法,如LSA会首先计算一个term-document矩阵,每一列表示每个文档中各个单词的出现频率,然后进行奇异值分解;HAL则会首先计算一个term-term共现矩阵。但此类方法会被频繁出现的the, and等单词影响,计算相似度的时候该类对语义影响很小的单词会占较大的比重。
- 基于上下文窗口的方法,如Word2Vec[1]。此类方法没有用到语料中的统计信息,可能无法捕捉到数据中的重复现象。
3.2 GloVe
为了解决上述两种方法存在的问题,文章提出了一种Global Vectors(GloVe)单词嵌入方法,可以直接捕获语料中的统计信息。
首先,我们计算单词共现矩阵 X X X,其中 X i j X_ij Xij表示单词 j j j出现在单词 i i i的上下文的次数。令 X i = ∑ k X i k X_i = \sum_k X_{ik} Xi=∑kXik表示任意单词出现在单词 i i i上下文的总次数,则 P i j = X i j X i P_{ij} = \frac {X_ij}{X_i} Pij=XiXij表示单词 j j j出现在单词 i i i的上下文的概率。
为了得到每个单词的嵌入 w i w_i wi,文章首先需要假设一种嵌入 w i , w j w_i, w_j wi,wj和共现矩阵之间的关系式。为此,文章给出一个示例:如下表所示,假设考虑单词i=“ice”,j=“steam”,则k="solid"时,由于"solid"和"ice"相关性更高,所以 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该大一点,下表中实验结果为8.9;如果k=“gas”,和"steam"的相关性更高,从而 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该小一点,下表中实验结果为 8.5 × 1 0 − 2 8.5 \times 10^{-2} 8.5×10−2;如果k="water"和二者均相关或k="fashion"和二者均不相关,则 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该接近1,如下表中的 1.36 1.36 1.36和 0.96 0.96 0.96。

为此,文章选择通过单词 i , j i,j i,j之间的概率比值来进行建模: F ( w i , w j , w ~ k ) = P i k P j k F(w_i, w_j, \tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F(wi,wj,w~k)=PjkPik,其中 w i , w j , w ~ k w_i, w_j, \tilde{w}_k wi,wj,w~k分别表示 i , j , k i, j, k i,j,k的词向量, w ~ \tilde{w} w~也是待学习的参数,和 w w w本质上没有区别,只是通过不同的初始化得到的,用于区分探针单词( k k k)和共现单词,类似transformer中的Q,K含义。考虑到单词空间一般是线性的,我们用 w i − w j w_i - w_j wi−wj表示向量之间的差异: F ( w i − w j , w ~ k ) = P i k P j k F(w_i- w_j, \tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F(wi−wj,w~k)=PjkPik,又因为上式左边的输入为两个向量,右边为标量,故我们考虑用向量的点积: F ( ( w i − w j ) T w ~ k ) = P i k P j k F((w_i -w_j)^T\tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F((wi−wj)Tw~k)=PjkPik。由于单词的共现矩阵中,单词和上下文单词是任意指定的,我们可以自由交换当前单词和上下文单词,从而我们要保证交换 w ↔ w ~ w \leftrightarrow \tilde{w} w↔w~和 X ↔ X T X \leftrightarrow X^T X↔XT后上式仍然成立,故我们首先需要 F F F为一个同态映射: F ( ( w i − w j ) T w ~ k ) = F ( w i T w ~ k ) F ( w j T w ~ k ) F((w_i -w_j)^T\tilde{w}_k) = \frac {F(w_i^T\tilde{w}_k)}{F(w_j^T\tilde{w}_k)} F((wi−wj)Tw~k)=F(wjTw~k)F(wiTw~k),从而有 F ( w i T w ~ k ) = P i k = X i k X i F(w_i^T\tilde{w}_k) = P_{ik} = \frac {X_{ik}}{X_i} F(wiTw~k)=Pik=XiXik。由于上式的解为 F = exp F=\exp F=exp,从而 exp ( w i T w ~ k ) = P i k = X i k X i ⟹ w i T w ~ k = log P i k = log ( X i k X i ) = log ( X i k ) − log ( X i ) \exp (w_i^T \tilde{w}_k) = P_{ik} = \frac {X_{ik}}{X_i}\\\implies w_i^T \tilde{w}_k = \log P_{ik} = \log \left(\frac {X_{ik}}{X_i}\right) = \log(X_{ik}) - \log (X_i) exp(wiTw~k)=Pik=XiXik⟹wiTw~k=logPik=log(XiXik)=log(Xik)−log(Xi);其次考虑到上式的 log ( X i ) \log (X_i) log(Xi)与 k k k无关,故可以写作偏差 b i b_i bi,再增加 w ~ k \tilde{w}_k w~k的偏差 b ~ k \tilde{b}_k b~k,我们得到 w i T w ~ k + b i + b ~ k = log ( x i k ) w_i^T \tilde{w}_k + b_i + \tilde{b}_k = \log(x_{ik}) wiTw~k+bi+b~k=log(xik)满足上述对称要求。在此基础上增加权重函数 f ( X i j ) f(X_{ij}) f(Xij)可以保证共现太频繁的元素不会被过分的重视,且稀有的共现元素也不会被过分重视。这就要求 f f f满足非递减且有明确上界,如下函数满足条件: f ( x ) = { ( x / x m a x ) α i f x < x m a x , 1 , o t h e r w i s e f(x) = \begin{cases}(x/x_{max})^{\alpha} \quad &if \ x < x_{max},\\1, \quad &otherwise \end{cases} f(x)={(x/xmax)α1,if x<xmax,otherwise。函数曲线如下图所示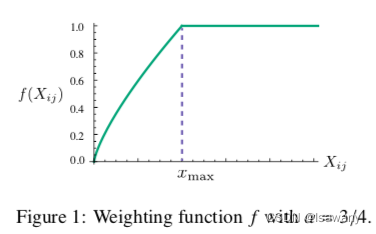
3.3 模型的复杂度
文章证明,当 α = 1.25 \alpha = 1.25 α=1.25时交过较好,此时模型的复杂度为 O ( ∣ C ∣ ) \mathcal{O}(|\mathcal{C}|) O(∣C∣),其中 C \mathcal{C} C表示语料库。相比于其他基于上下文窗口的方法复杂度 O ( V 2 ) \mathcal{O}(V^2) O(V2)更低。
4. 文章亮点
文章提出了基于将上下文窗口和共现矩阵结合的词向量嵌入方法GloVe,数值实验表明,GloVe在单词相似度、单词类比和NER等任务上相比于其他SOTA方法有明显提升。
5. 原文传送门
[GloVe: Global Vectors for Word Representation](GloVe: Global Vectors for Word Representation)
6. References
[1] 论文笔记–Efficient Estimation of Word Representations in Vector Space
相关文章:

论文笔记--GloVe: Global Vectors for Word Representation
论文笔记--GloVe: Global Vectors for Word Representation 1. 文章简介2. 文章概括3 文章重点技术3.1 两种常用的单词向量训练方法3.2 GloVe3.3 模型的复杂度 4. 文章亮点5. 原文传送门6. References 1. 文章简介 标题:GloVe: Global Vectors for Word Representa…...
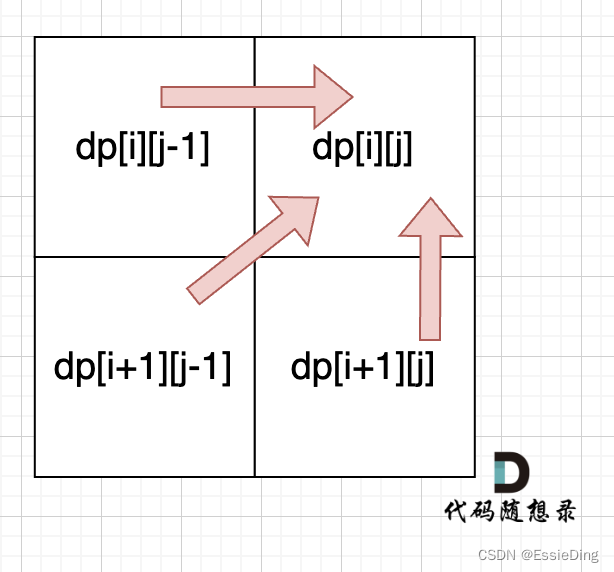
day57|● 647. 回文子串 ● 516.最长回文子序列
647. 回文子串 https://leetcode.cn/problems/palindromic-substrings/solution/by-lfool-2mvg/ Given a string s, return the number of palindromic substrings in it. A string is a palindrome when it reads the same backward as forward. A substring is a contiguous…...

docker compose.yml学习
docker compose 安装docker-compose sudo curl -L "https://github.com/docker/compose/releases/download/v2.2.2/docker-compose-$(uname -s)-$(uname -m)" -o /usr/local/bin/docker-composechmod x /usr/local/bin/docker-composeln -s /usr/local/bin/docker-…...
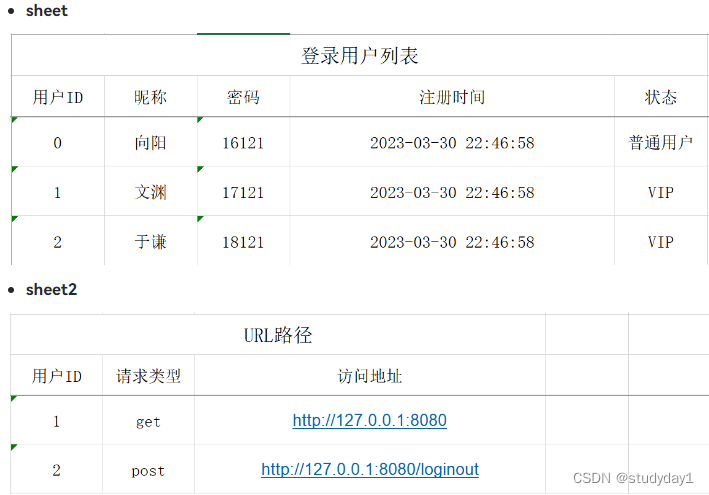
【业务功能篇55】Springboot+easyPOI 导入导出
Apache POI是Apache软件基金会的开源项目,POI提供API给Java程序对Microsoft Office格式档案读和写的功能。 Apache POI 代码实现复杂,学习成本较高。 Easypoi 功能如同名字easy,主打的功能就是容易,让一个没见接触过poi的人员 就可以方便的写出Excel导出…...
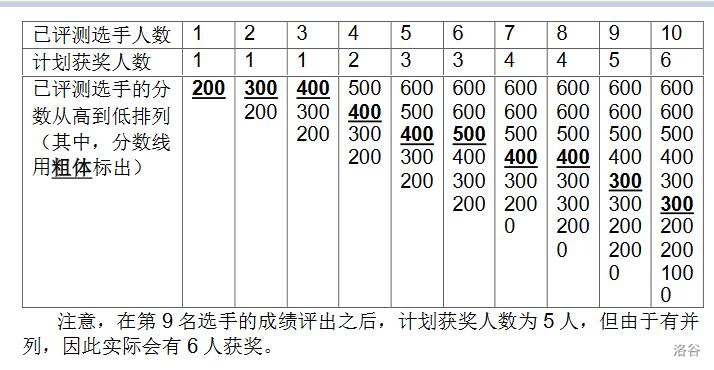
对顶堆算法
对顶堆可以动态维护一个序列上的第k大的数,由一个大根堆和一个小根堆组成, 小根堆维护前k大的数(包含第k个)大根堆维护比第k个数小的数 [CSP-J2020] 直播获奖 题目描述 NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩&a…...

node.js的优点
提示:node.js的优点 文章目录 一、什么是node.js二、node.js的特性 一、什么是node.js 提示:什么是node.js? Node.js发布于2009年5月,由Ryan Dahl开发,是一个基于ChromeV8引擎的JavaScript运行环境,使用了一个事件驱…...

golang编译跨平台
golang可以在windows上编译出linux、MacOS等系统上的程序。 go编译器windows下可变翼linux程序,例如,GOARCHamd64 和 GOOSlinux 可以用于编译 64 位的 Linux 平台上的可执行文件。: set GOARCHamd64 set GOOSlinux go build main.go通过设置…...

关于Spring的bean的相关注解以及其简单使用方法
一、前置工作 第一步:创建一个maven项目 第二步:在resource中创建一个名字叫做spring-config.xml的文件,并把以下代码复制粘贴 <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.sprin…...

【计算机视觉】BLIP:源代码示例demo(含源代码)
文章目录 一、Image Captioning二、VQA三、Feature Extraction四、Image-Text Matching 一、Image Captioning 首先配置代码: import sys if google.colab in sys.modules:print(Running in Colab.)!pip3 install transformers4.15.0 timm0.4.12 fairscale0.4.4!g…...

TWILIGHT靶场详解
TWILIGHT靶场详解 下载地址:https://download.vulnhub.com/sunset/twilight.7z 这是一个比较简单的靶场,拿到IP后我们扫描发现开启了超级多的端口 其实这些端口一点用都没有,在我的方法中 但是也有不同的方法可以拿权限,就需要…...

【案例】--GPT衍生应用案例
目录 一、前言二、GPT实现智能问答架构2.1、基本的GPT实现智能问答架构2.2、可应用的GPT实现智能问答架构1、语义转换2、相似度关键字矩阵3、ES中搜索相似度关键字矩阵三、后续一、前言 GPT,全称Generative Pre-trained Transformer ,中文名可译作生成式预训练Transformer。…...

Sip网络音频对讲广播模块, sip网络寻呼话筒音频模块
Sip网络音频对讲广播模块, sip网络寻呼话筒音频模块 一、模块介绍 SV-2101VP和 SV-2103VP网络音频对讲广播模块 是一款通用的独立SIP音频功能模块,可以轻松地嵌入到OEM产品中。该模块对来自网络的SIP协议及RTP音频流进行编解码。 该模块支持多种网络协议…...
)
leetcode1219. 黄金矿工(java)
黄金矿工 leetcode1219. 黄金矿工题目描述回溯算法代码 回溯算法 leetcode1219. 黄金矿工 难度: 中等 eetcode 1219 黄金矿工 题目描述 你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元…...

Svelte框架入门
关键词 前端框架、编译器、响应式、模板 介绍 Svelte /svelt/ adj. 苗条的;线条清晰的;和蔼的 Svelte是一个前端组件框架,就像它的英文名字一样,Svelte的目标是打造一个更高性能的响应性前端框架。 Svelte类似于React和Vue框架&am…...
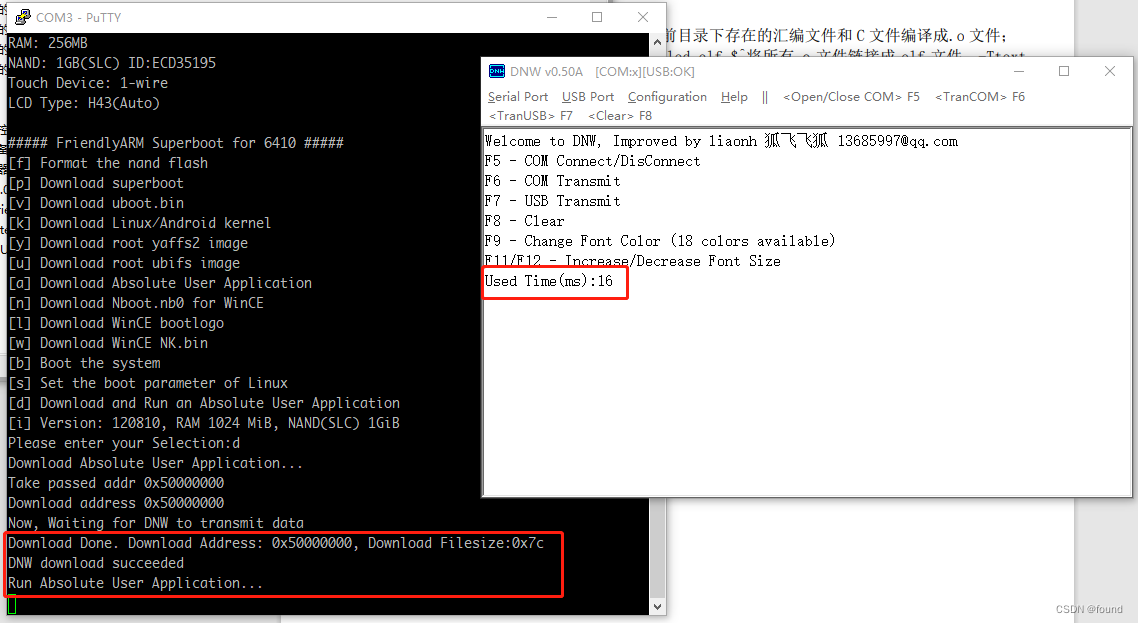
在linux中进行arm交叉编译体验tiny6410裸机程序开发流程
在某鱼上找了一个友善之臂的Tiny6410开发板用来体验一下嵌入式开发。这次先体验一下裸机程序的开发流程,由于这个开发板比较老旧了,官方文档有很多过期的内容,所以记录一下整个过程。 1. 交叉编译器安装 按照光盘A中的文档《04- Tiny6410 L…...
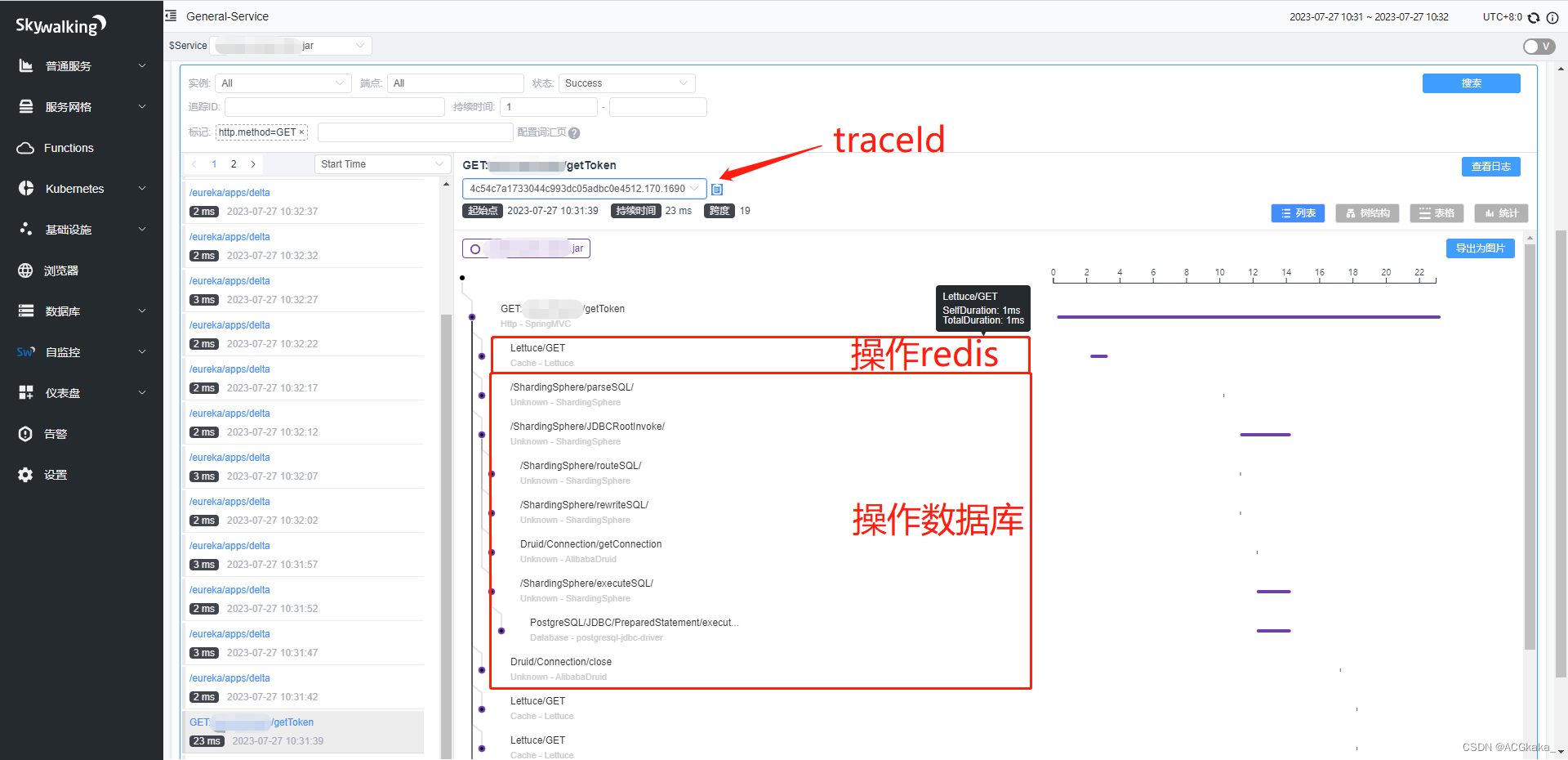
SpringBoot实战(二十三)集成 SkyWalking
目录 一、简介二、拉取镜像并部署1.拉取镜像2.运行skywalking-oap容器3.运行skywalking-ui容器4.访问页面 三、下载解压 agent1.下载2.解压 四、创建 skywalking-demo 项目1.Maven依赖2.application.yml3.DemoController.java 五、构建启动脚本1.startup.bat2.执行启动脚本3.发…...
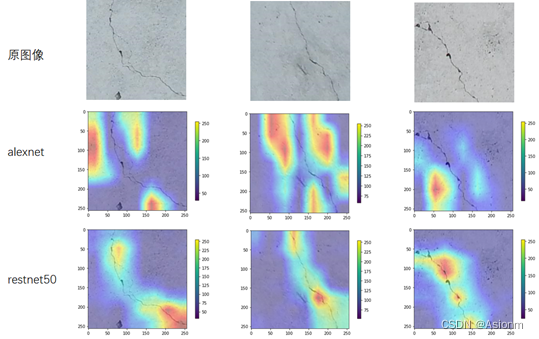
深度学习实践——卷积神经网络实践:裂缝识别
深度学习实践——卷积神经网络实践:裂缝识别 系列实验 深度学习实践——卷积神经网络实践:裂缝识别 深度学习实践——循环神经网络实践 深度学习实践——模型部署优化实践 深度学习实践——模型推理优化练习 深度学习实践——卷积神经网络实践ÿ…...
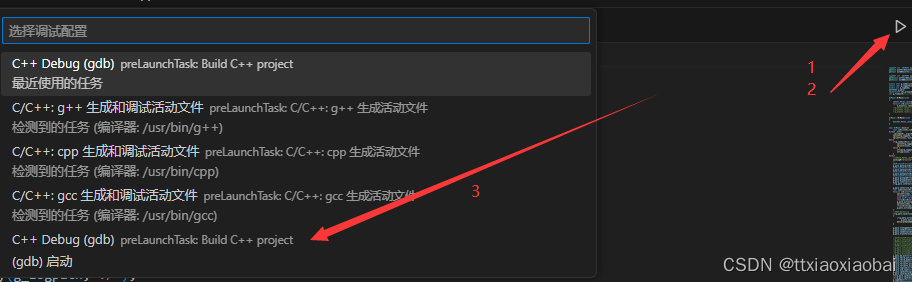
linux | vscode | makefile | c++编译和调试
简单介绍环境: vscode 、centos、 gcc、g、makefile 简单来说就是,写好项目然后再自己写makefile脚本实现编译。所以看这篇博客的用户需要了解gcc编译的一些常用命令以及makefile语法。在网上看了很多教程,以及官网也看了很多次,最…...

Spring | Bean 作用域和生命周期
一、通过一个案例来看 Bean 作用域的问题 Spring 是用来读取和存储 Bean,因此在 Spring 中 Bean 是最核心的操作资源,所以接下来我们深入学习⼀下 Bean 对象 假设现在有⼀个公共的 Bean,提供给 A 用户和 B 用户使用,然而在使用的…...
)
培训(c++题解)
题目描述 某培训机构的学员有如下信息: 姓名(字符串)年龄(周岁,整数)去年 NOIP 成绩(整数,且保证是 5 的倍数) 经过为期一年的培训,所有同学的成绩都有所提…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
