有限差法(Finite Difference)求梯度和Hessian Matrix(海森矩阵)的python实现
数学参考
有限差方法求导,Finite Difference Approximations of Derivatives,是数值计算中常用的求导方法。数学上也比较简单易用。本文主要针对的是向量值函数,也就是f(x):Rn→Rf(x):\mathbb{R^n}\rightarrow \mathbb{R}f(x):Rn→R当然,普通的标量值函数是向量值函数的一种特例。
本文采用的数学参考是:有限差方法
参考的主要是Central Difference Approximations小节中的Second-order derivatives based on gradient calls的那个公式。
代码
准备
本文的方法只需要numpy包,几乎可以说不需要任何包,而且不受到什么限制,只要满足输入格式就能求取,比所谓autograd,numdifftools好用的多。
梯度函数
为了求Hessian矩阵,本文采用的方法需要首先求取梯度。首先需要有一个函数func,示例的func如下:
def func(x, **args):x_0 = x[0]x_1 = x[1]return x_0**2 + x_1**2
该函数是一个R2→R\mathbb{R^2}\rightarrow \mathbb{R}R2→R的函数。将该函数输入进下面的函数grad_func_generator中之后,就可以返回梯度函数,支持在任何一点求取梯度。这里输入x应该是一个列表,是各个维度的输入。例如x = [0,0].
def grad_func_generator(func, eps = 0.00001):def gradient_func(point):n_var = len(point)gradient = np.zeros(n_var, np.float32)# nth gradientfor i in range(n_var):# 初始化左点和右点,同时不改变原来的展开点left_point = point.copy()right_point = point.copy()left_point[i] = point[i] - epsright_point[i] = point[i] + epsgradient[i] = (func(right_point) - func(left_point))/(2*eps)return gradientreturn gradient_func
求取梯度:
grad_f = grad_func_generator(func) # 生成梯度函数
grad_f([1,1])
可以得到结果:
array([2., 2.], dtype=float32)
Hessian矩阵
利用已经实现的梯度函数,可以实现Hessian矩阵。
def hessian(func, point = [0, 0], eps = 0.00001):"""Hessian matrix of func at expendung point."""n_var = len(point)def grad_func_generator(func):def gradient_func(point):gradient = np.zeros(n_var, np.float32)# nth gradientfor i in range(n_var):# 初始化左点和右点,同时不改变原来的展开点left_point = point.copy()right_point = point.copy()left_point[i] = point[i] - epsright_point[i] = point[i] + epsgradient[i] = (func(right_point) - func(left_point))/(2*eps)return gradientreturn gradient_funcgrad_func = grad_func_generator(func)hessian_matrix = np.zeros((n_var, n_var), np.float32)for i in range(n_var):for j in range(n_var):# 第一项left_point_j = point.copy()right_point_j = point.copy()right_point_j[j] = point[j] + epsleft_point_j[j] = point[j] - epsdiff_i = (grad_func(right_point_j)[i] - grad_func(left_point_j)[i])/(4*eps)# 第二项left_point_i = point.copy()right_point_i = point.copy()right_point_i[i] = point[i] + epsleft_point_i[i] = point[i] - epsdiff_j = (grad_func(right_point_i)[j] - grad_func(left_point_i)[j])/(4*eps)hessian_matrix[i, j] = diff_i + diff_jreturn hessian_matrix
可以通过输入函数func和求取二阶导数的点x,就可以输出该点处的Hessian矩阵。
hessian(func, [0,0])
得到结果
array([[2., 0.],[0., 2.]], dtype=float32)
如果和numdifftools的结果对照,可以发现一样。但是numdifftools非常难用,总是报错。我们的程序只需要numpy包就能实现,非常方便好用。
相关文章:
求梯度和Hessian Matrix(海森矩阵)的python实现)
有限差法(Finite Difference)求梯度和Hessian Matrix(海森矩阵)的python实现
数学参考 有限差方法求导,Finite Difference Approximations of Derivatives,是数值计算中常用的求导方法。数学上也比较简单易用。本文主要针对的是向量值函数,也就是f(x):Rn→Rf(x):\mathbb{R^n}\rightarrow \mathbb{R}f(x):Rn→R当然&…...

day33 贪心算法 | 1005、K次取反后最大化的数组和 134、加油站 135、分发糖果
题目 1005、K次取反后最大化的数组和 给定一个整数数组 A,我们只能用以下方法修改该数组:我们选择某个索引 i 并将 A[i] 替换为 -A[i],然后总共重复这个过程 K 次。(我们可以多次选择同一个索引 i。) 以这种方式修改…...

《蓝桥杯每日一题》递推·AcWing 3777. 砖块
1.题目描述n 个砖块排成一排,从左到右编号依次为 1∼n。每个砖块要么是黑色的,要么是白色的。现在你可以进行以下操作若干次(可以是 0 次):选择两个相邻的砖块,反转它们的颜色。(黑变白…...
)
mysql读写分离(maxscale)
1. 环境架构 需要三台服务器。192.168.2.10(master)192.168.2.20(slave)192.168.2.30(maxscale) 2. 部署mysql主从同步 mysql主从同步可以参考mysql主从同步 3. 部署maxscale服务 MaxScale中间件软件 …...
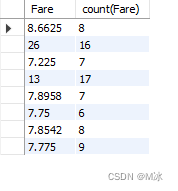
第八章 - 数据分组( group by , having , select语句顺序)
第八章 - 数据分组 group by数据分组过滤分组 having分组排序groub by语句的一些规定select语句顺序数据分组 在使用group by进行分组时,一般都会配合聚合函数一起使用,实现统计数据的功能。比如下面例子,需要按性别计算人数。按性别进行分组…...

Git(GitHub,Gitee 码云,GitLab)详细讲解
目录第一章 Git 概述1.1 何为版本控制1.2 为什么需要版本控制1.3 版本控制工具1.4 Git 简史1.5 Git 工作机制1.6 Git 和代码托管中心第二章 Git 安装第三章 Git 常用命令3.1 设置用户签名3.2 初始化本地库3.3 查看本地库状态3.3.1 首次查看(工作区没有任何文件&…...
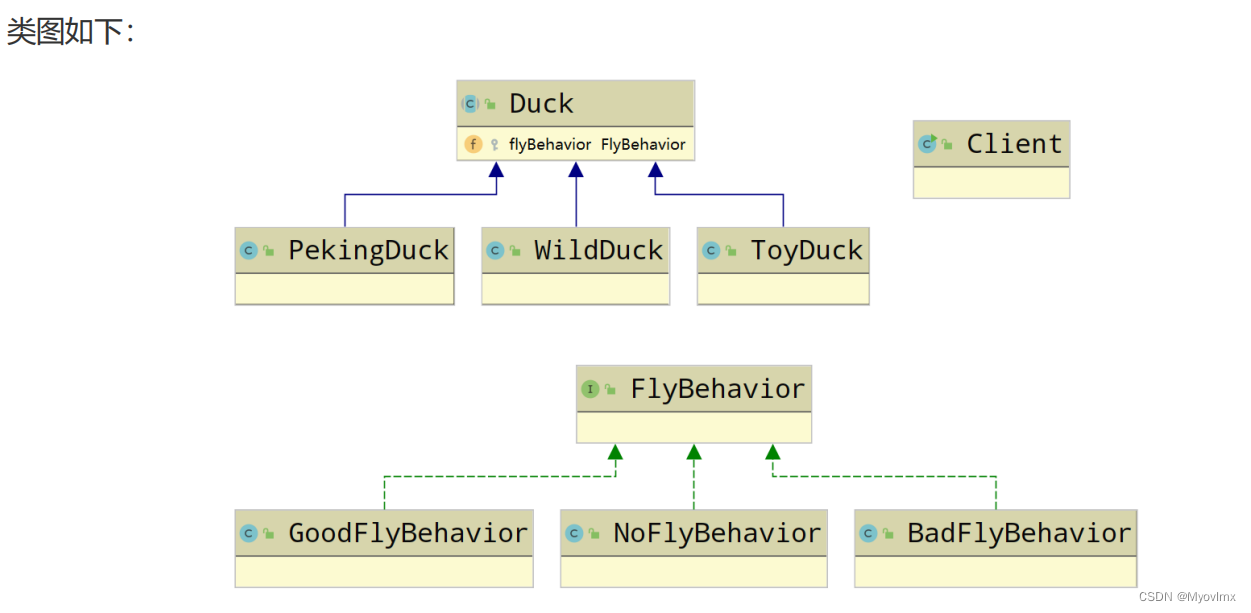
策略模式(Strategy Pattern)
编写鸭子项目,具体要求如下: 1) 有各种鸭子(比如 野鸭、北京鸭,水鸭等,鸭子有各种行为,比如 叫,飞行等) 2)显示鸭子的信息 传统方案解决鸭子问题 1࿰…...
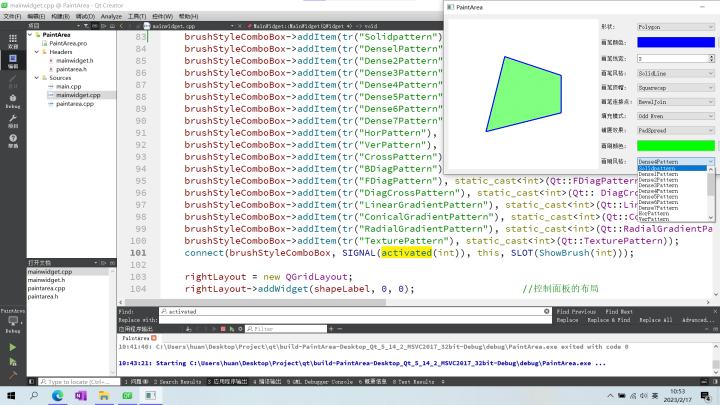
《Qt6开发及实例》6-2 Qt6基础图形的绘制
目录 一、绘图框架设计 二、绘图区的实现 2.1 PaintArea类 2.2 PaintArea类讲解 三、主窗口的实现 3.1 MainWidget类 3.2 MainWidget类讲解 3.3 槽函数编写 3.5 其他内容 一、绘图框架设计 界面 两个类 二、绘图区的实现 2.1 PaintArea类 paintarea.h #ifndef…...

LeetCode 382. 链表随机节点
原题链接 难度:middle\color{orange}{middle}middle 题目描述 给你一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点 被选中的概率一样 。 实现 SolutionSolutionSolution 类: Solution(ListNodehead)Solution…...
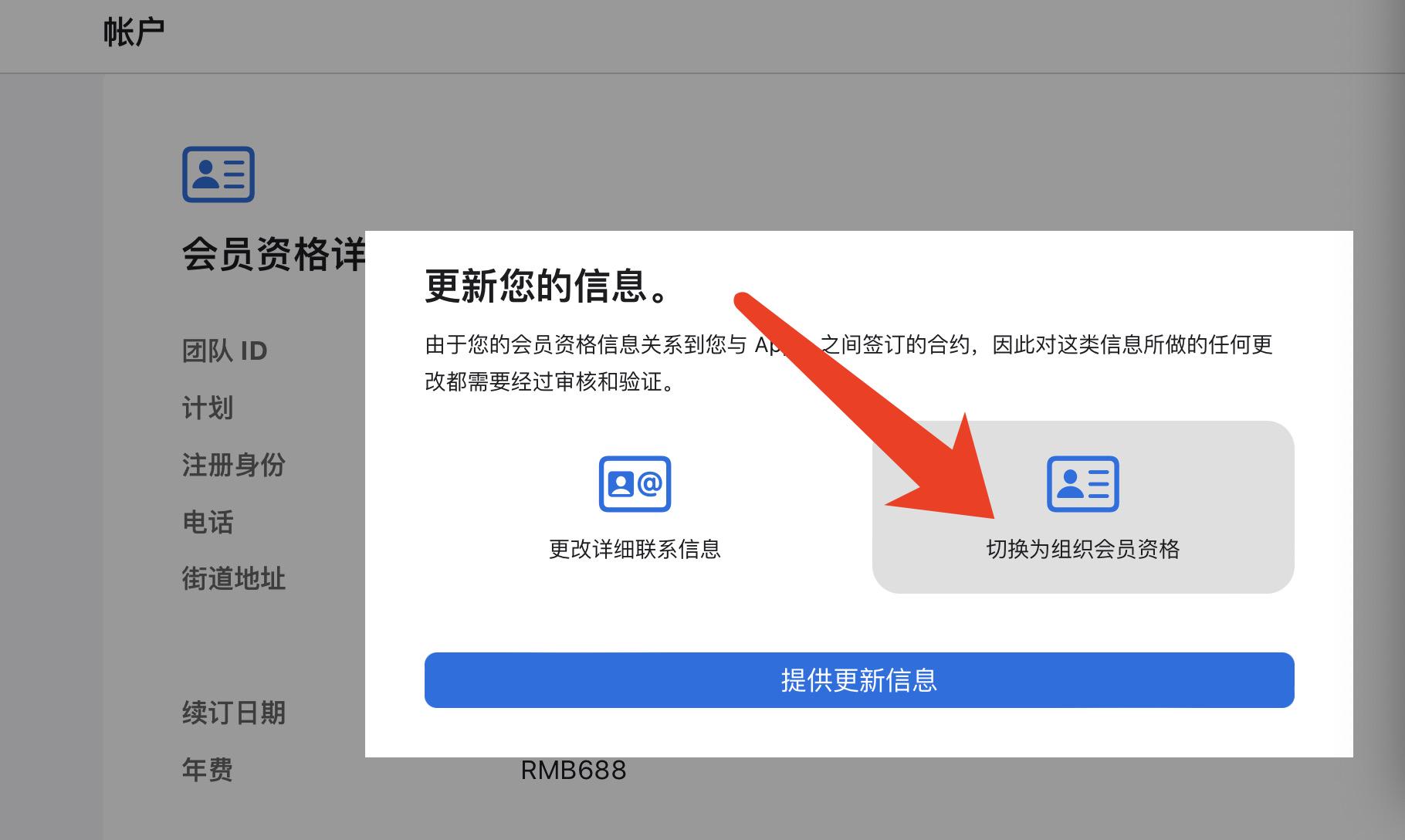
iOS开发AppleDeveloper中给别人授权开发者权限后,对方一直显示不了我的开发账号team
在iOS开发经常出现多人协作开发的情况。这时我们通常要发邮件邀请别的用户为开发者或者app管理就可以开发我们自己的项目了。但是这次我给别人授权开发者权限后,发现别人权限中没有证书相关权限如图:并且别人登录该账号后,在xcode中只有一个看…...

FreeRTOS数据类型和编程规范
目录 数据类型 变量名 函数名 宏的名 数据类型 每个移植的版本都含有自己的portmacro.h头文件,里面定义了2个数据类型 TickType_t FreeRTOS配置了一个周期性的时钟中断:Tick Interrupt每发生一次中断,中断次数累加,这被称为t…...
【python知识】win10下如何用python将网页转成pdf文件
一、说明 本篇记录一个自己享用的简单工具。在大量阅读网上文章中,常常遇到一个专题对应多篇文章,用浏览器的收藏根本不够。能否见到一篇文章具有搜藏价值,就转到线下,以备日后慢慢消化吸收。这里终于找到一个办法,将在…...
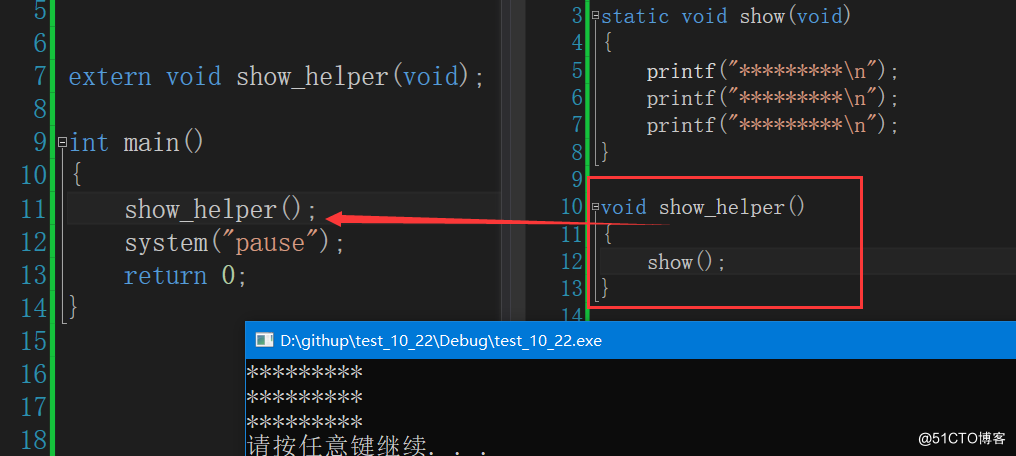
C语言常见关键字
写在前面 这个博客是结合C语言深度解剖这本书和我以前学的知识综合而成的,我希望可以更见详细的谈一下C语言的关键字,内容有点多,有错误还请斧正. 常见关键字 下面我们说下C语言的关键字,所谓的关键字是指具有特定功能的单词,我们可以使用关键字来帮助我们完成不同的事物.C语…...

【MT7628】固件开发-SDK4320添加MT7612E WiFi驱动操作说明
解压5G WiFi MT7612E驱动1.1解压指令 tar -xvf MT76x2E_MT7620_LinuxAP_V3.0.4.0_P2_DPA_20160308.tar.bz2 1.2解压之后会出现以下两个目录 rlt_wifi rlt_wifi_ap 1.3将解压后的文件拷贝到系统下 拷贝路径 RT288x_SDK/source/linux-2.6.36.x/drivers/net/wireless 内核中打开驱…...
如何从手工测试进阶自动化测试?阿里10年测开经验分享...
随着行业的竞争加剧,互联网产品迭代速度越来越快,QA 与测试工程师都需要在越来越短的测试周期内充分保证质量。可是,App 测试面临着很多挑战,比如多端发布、多版本发布、多机型发布等等,导致了手工测试很难完全胜任。因…...
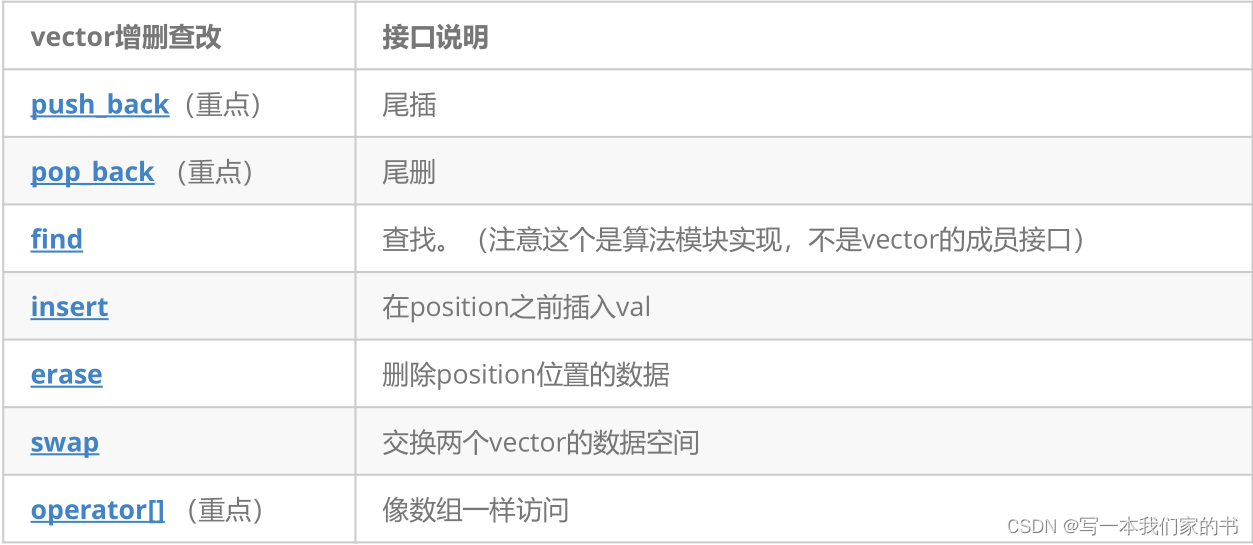
C++复习笔记11
1. vector是表示可变大小数组的序列容器。 2. 就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素进行访问,和数组一样高效。但是又不像数组,它的大小是可以动态改变的,而且它的大小会被…...

【MT7628】固件开发-SDK4320添加MT7628 WiFi驱动操作说明
解压2.4G WiFi MT7628驱动1.1解压指令 tar -xvf MT7628_LinuxAP_V4.1.0.0_DPA_20160310.tar.bz2 1.2解压之后会出现以下两个目录 mt_wifi mt_wifi_ap 1.3将解压后的文件拷贝到系统下 拷贝路径 RT288x_SDK/source/linux-2.6.36.x/drivers/net/wireless 内核中打开驱动编译修改R…...

C#开发的OpenRA游戏加载界面的实现
C#开发的OpenRA游戏加载界面的实现 游戏的UI是一个游戏必备, 但是游戏的UI都是自己处理的,不能使用像Windows自带的UI。 这样游戏的UI,其实也是使用游戏的方式来显示的, 只不过使用了低帧率的方式来显示。 比如OpenRA游戏界面,就会显示如下: 游戏的界面有很多,先从一个简…...

渲染农场优势是什么_云渲染农场怎么用?
在回答渲染农场的优势这个问题之前,我先申明一下本文中提到的渲染农场/云渲染平台/云渲染农场,都特指CG领域内的专业3D渲染平台,有一些文章会强调这个叫法的区别,但是业内一般都不会分这么细,所以也就不赘述了。渲染农…...

SoapUI、Jmeter、Postman三种接口测试工具的比较分析
目录 前言 1. 用例组织方式 2. 支持的接口类型与测试类型 3. 配置不同接口类型 4. 自定义变量以及变量的作用域 5. 数据源、生成器,进行参数化 6. 流程控制 7. 结果解析、展示 8. 断言 9. 脚本扩展能力 10. 团队协作 总结 重点:配…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
