机器学习十大经典算法
机器学习算法是计算机科学和人工智能领域的关键组成部分,它们用于从数据中学习模式并作出预测或做出决策。本文将为大家介绍十大经典机器学习算法,其中包括了线性回归、逻辑回归、支持向量机、朴素贝叶斯、决策树等算法,每种算法都在特定的领域发挥着巨大的价值。
1 线性回归
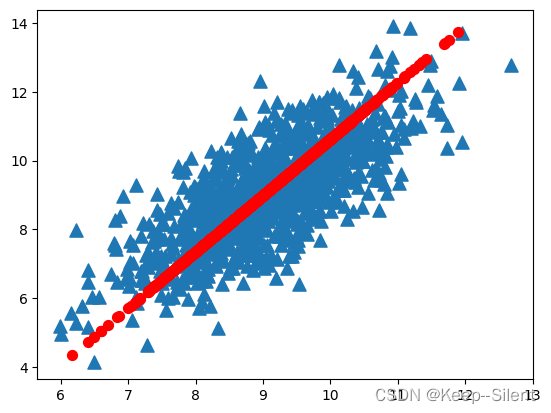
线性回归算得上是最流行的机器学习算法之一,它是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,目前线性回归的运用十分广泛。线性回归就是要找一条直线,并且让这条直线尽可能地拟合散点图中的数据点。它试图通过将直线方程与该数据拟合来表示自变量(x 值)和数值结果(y 值)。然后就可以用这条线来预测未来的值!这种算法最常用的技术是最小二乘法。这个方法计算出最佳拟合线,以使得与直线上每个数据点的垂直距离最小。总距离是所有数据点的垂直距离(绿线)的平方和。其思想是通过最小化这个平方误差或距离来拟合模型。
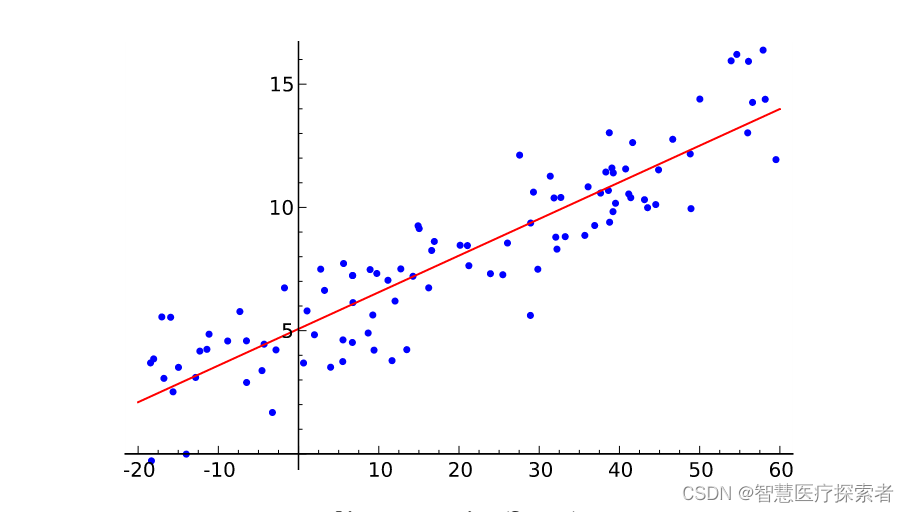
算法详细讲解:机器学习之线性回归模型
2 逻辑回归
逻辑回归(Logistic regression)与线性回归类似,但它是用于输出为二进制的情况(即,当结果只能有两个可能的值)。对最终输出的预测是一个非线性的 S 型函数,称为 logistic function, g()。
这个逻辑函数将中间结果值映射到结果变量 Y,其值范围从 0 到 1。然后,这些值可以解释为 Y 出现的概率。S 型逻辑函数的性质使得逻辑回归更适合用于分类任务。
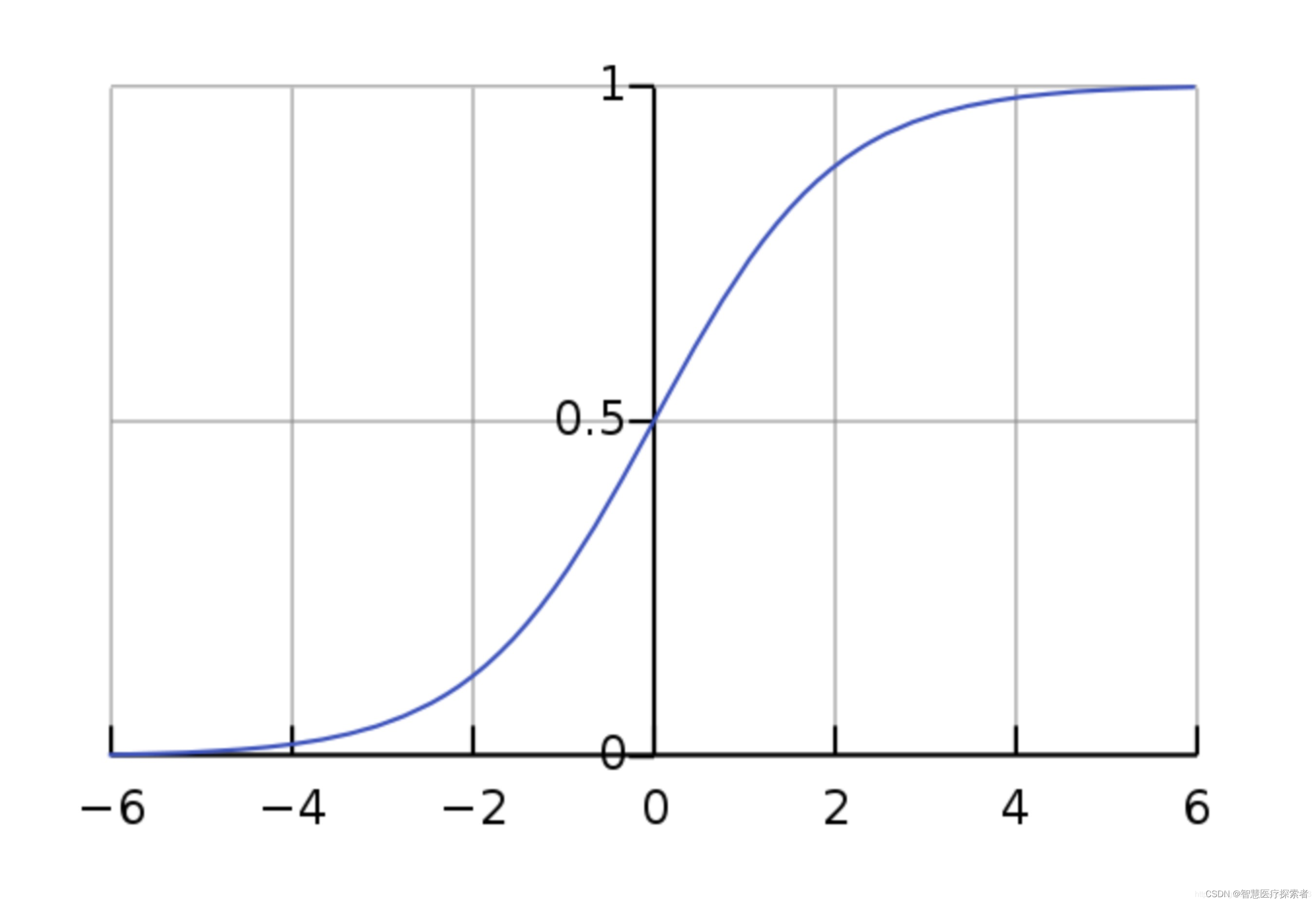
算法详细讲解:机器学习之逻辑回归
3 K近邻算法
K- 最近邻算法(K-Nearest Neighbors,KNN)非常简单。KNN 通过在整个训练集中搜索 K 个最相似的实例,即 K 个邻居,并为所有这些 K 个实例分配一个公共输出变量,来对对象进行分类。
K 的选择很关键:较小的值可能会得到大量的噪声和不准确的结果,而较大的值是不可行的。它最常用于分类,但也适用于回归问题。
用于评估实例之间相似性的距离可以是欧几里得距离(Euclidean distance)、曼哈顿距离(Manhattan distance)或明氏距离(Minkowski distance)。欧几里得距离是两点之间的普通直线距离。它实际上是点坐标之差平方和的平方根。
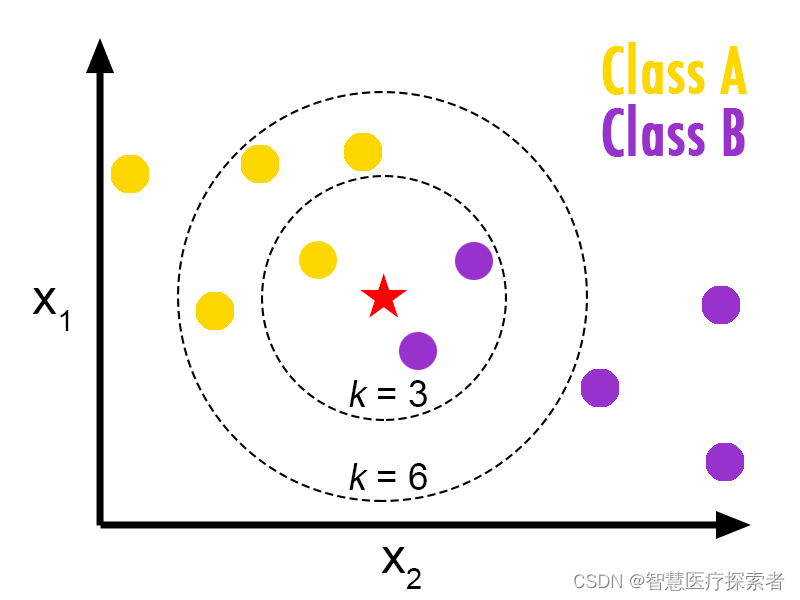
算法详细讲解:机器学习之K紧邻算法
4 K-均值算法
K- 均值(K-means)是通过对数据集进行分类来聚类的。例如,这个算法可用于根据购买历史将用户分组。它在数据集中找到 K 个聚类。K- 均值用于无监督学习,因此,我们只需使用训练数据 X,以及我们想要识别的聚类数量 K。
该算法根据每个数据点的特征,将每个数据点迭代地分配给 K 个组中的一个组。它为每个 K- 聚类(称为质心)选择 K 个点。基于相似度,将新的数据点添加到具有最近质心的聚类中。这个过程一直持续到质心停止变化为止。
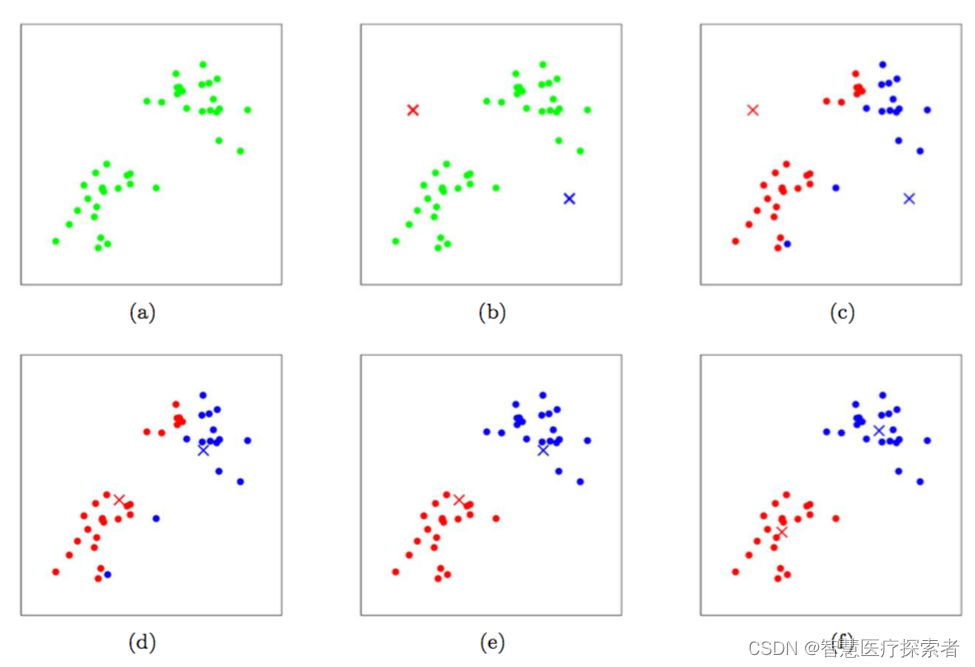
算法详细讲解:机器学习之K-均值算法
5 支持向量机
支持向量机(support vector machine,SVM)是有监督学习中最有影响力的机器学习算法之一,该算法的诞生可追溯至上世纪 60 年代, 前苏联学者 Vapnik 在解决模式识别问题时提出这种算法模型,此后经过几十年的发展直至 1995 年, SVM 算法才真正的完善起来,其典型应用是解决手写字符识别问题。
SVM 是一种非常优雅的算法,有着非常完善的数学理论基础,其预测效果,在众多机器学习模型中“出类拔萃”。在深度学习没有普及之前,“支持向量机”可以称的上是传统机器学习中的“霸主”。
支持向量机是一种二分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。支持向量机的学习算法是求解凸二次规划的最优化算法。
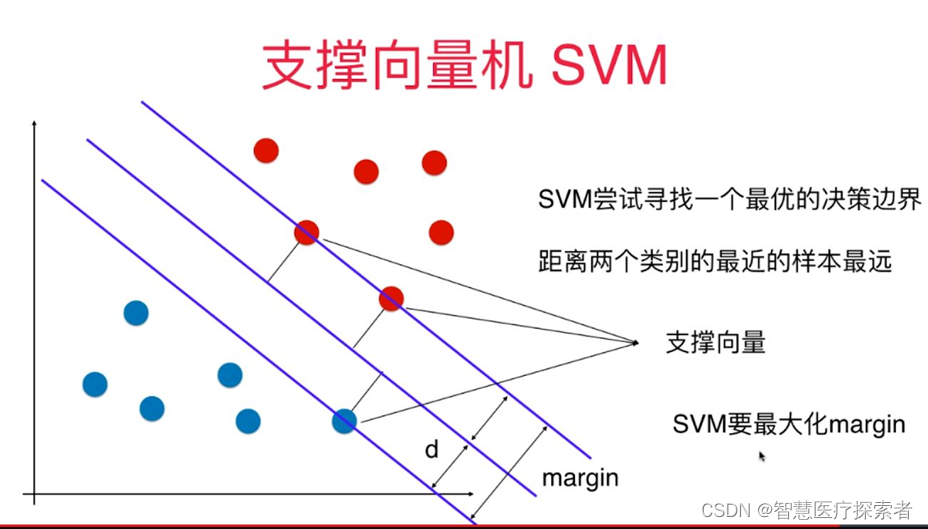
算法详细讲解:机器学习之支持向量机
6 朴素贝叶斯
朴素贝叶斯是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率,是应用最为广泛的分类算法之一。
朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
朴素贝叶斯对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
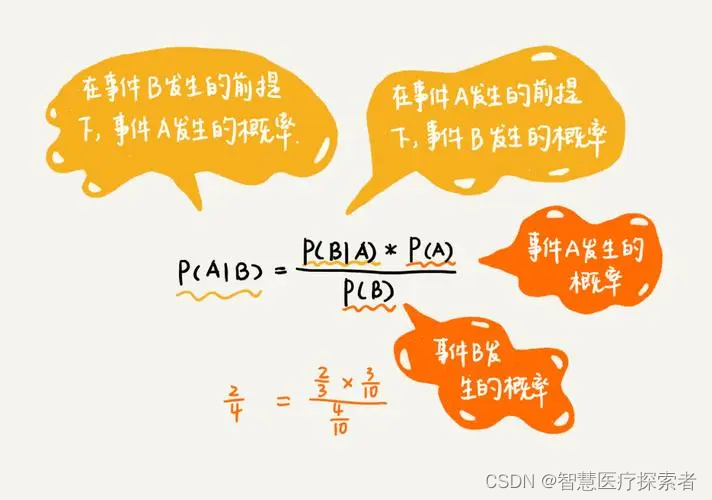
算法详细讲解:机器学习之朴素贝叶斯
7 决策树
决策树(Decision Tree,又称为判定树)算法是机器学习中常见的一类算法,是一种以树结构形式表达的预测分析模型。决策树属于监督学习(Supervised learning),根据处理数据类型的不同,决策树又为分类决策树与回归决策树。最早的的决策树算法是由Hunt等人于1966年提出,Hunt算法是许多决策树算法的基础,包括ID3、C4.5和CART等。
决策树可用于回归和分类任务。在这一算法中,训练模型通过学习树表示(Tree representation)的决策规则来学习预测目标变量的值。树是由具有相应属性的节点组成的。在每个节点上,我们根据可用的特征询问有关数据的问题。左右分支代表可能的答案。最终节点(即叶节点)对应于一个预测值。每个特征的重要性是通过自顶向下方法确定的。节点越高,其属性就越重要。
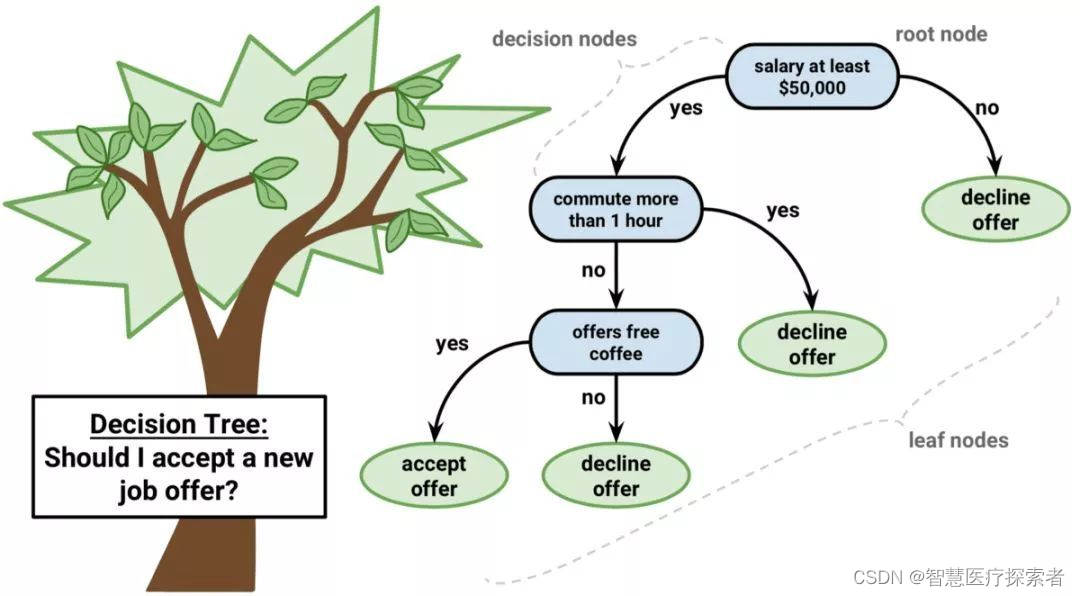
算法详细讲解:机器学习之决策树
8 随机森林
随机森林(Random Forest)是一种非常流行的集成机器学习算法。这个算法的基本思想是,许多人的意见要比个人的意见更准确。在随机森林中,我们使用决策树集成。为了对新对象进行分类,我们从每个决策树中进行投票,并结合结果,然后根据多数投票做出最终决定。
随机森林算法由于其良好的性能和可解释性,适用于许多不同的应用场景。在分类问题、回归问题、特征选择、异常检测等多种场景中发挥重要作用。
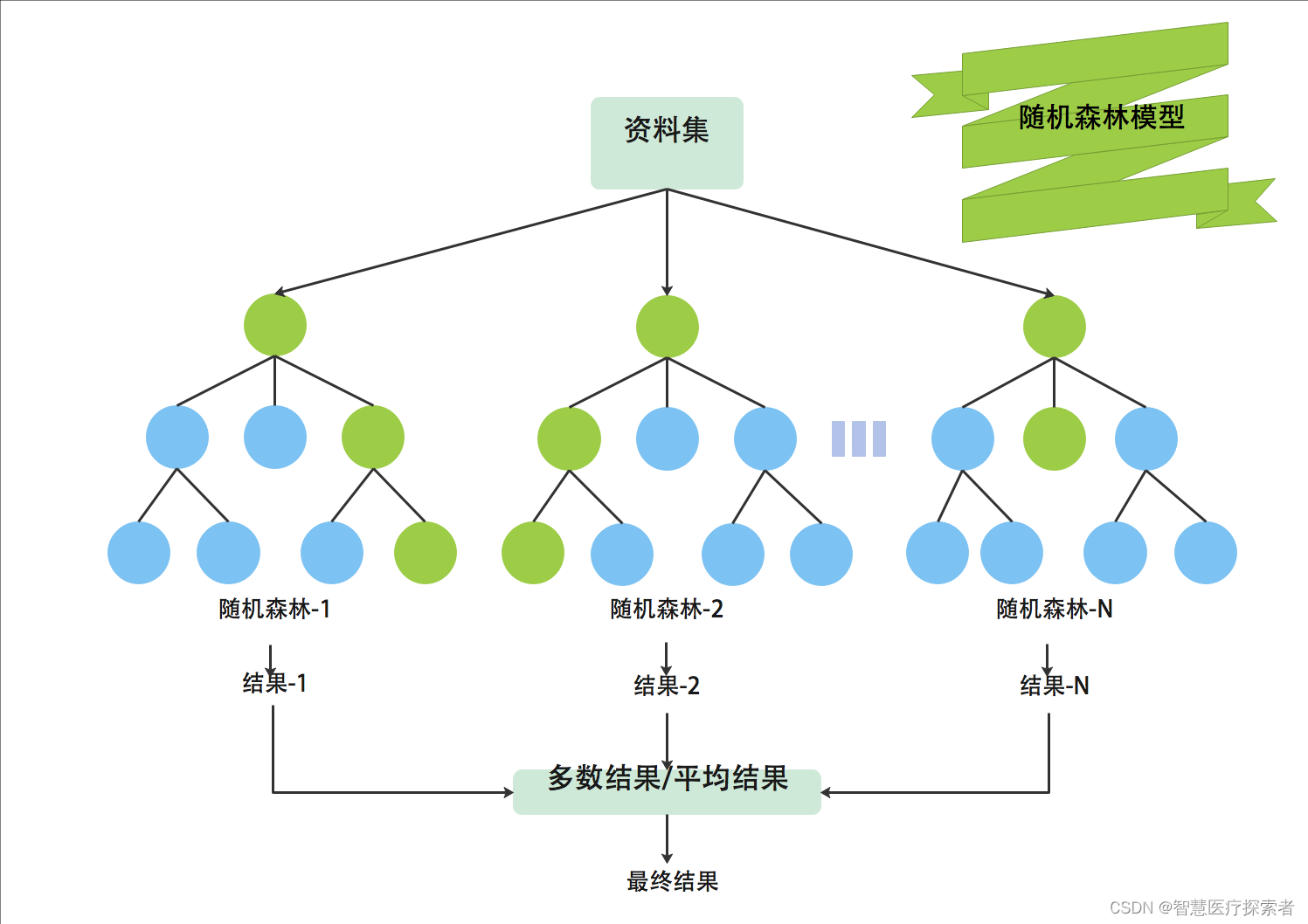
算法详细讲解:机器学习之随机森林
9 主成分分析
主成分分析(Principal Component Analysis)简称PCA,是一个非监督学习的机器学习算法,主要用于数据的降维,对于高维数据,通过降维,可以发现更便于人类理解的特征。
PCA是实现数据降维的一种算法。正如其名,假设有一份数据集,每条数据的维度是D,PCA通过分析这D个维度的前K个主要特征(这K个维度在原有D维特征的基础上重新构造出来,且是全新的正交特征),将D维的数据映射到这K个主要维度上进而实现对高维数据的降维处理。 PCA算法所要达到的目标是,降维后的数据所损失的信息量应该尽可能的少,即这K个维度的选取应该尽可能的符合原始D维数据的特征。
算法详细讲解:机器学习之主成分分析
10 Boosting和AdaBoost
Boosting 是一种试图利用大量弱分类器创建一个强分类器的集成技术。要实现 Boosting 方法,首先你需要利用训练数据构建一个模型,然后创建第二个模型(它企图修正第一个模型的误差)。直到最后模型能够对训练集进行完美地预测或加入的模型数量已达上限,我们才停止加入新的模型。
AdaBoost 是第一个为二分类问题开发的真正成功的 Boosting 算法。它是人们入门理解 Boosting 的最佳起点。当下的 Boosting 方法建立在 AdaBoost 基础之上,最著名的就是随机梯度提升机。
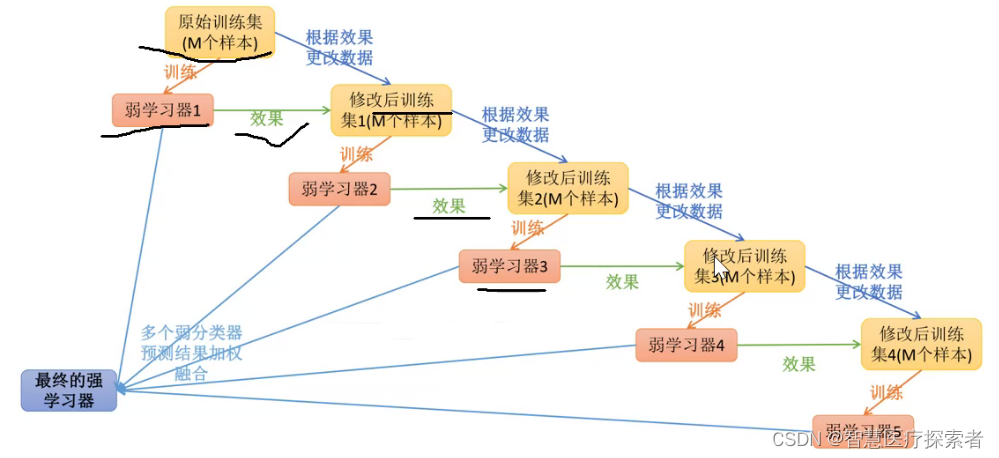
算法详细讲解:机器学习之Boosting和AdaBoos
相关文章:

机器学习十大经典算法
机器学习算法是计算机科学和人工智能领域的关键组成部分,它们用于从数据中学习模式并作出预测或做出决策。本文将为大家介绍十大经典机器学习算法,其中包括了线性回归、逻辑回归、支持向量机、朴素贝叶斯、决策树等算法,每种算法都在特定的领…...
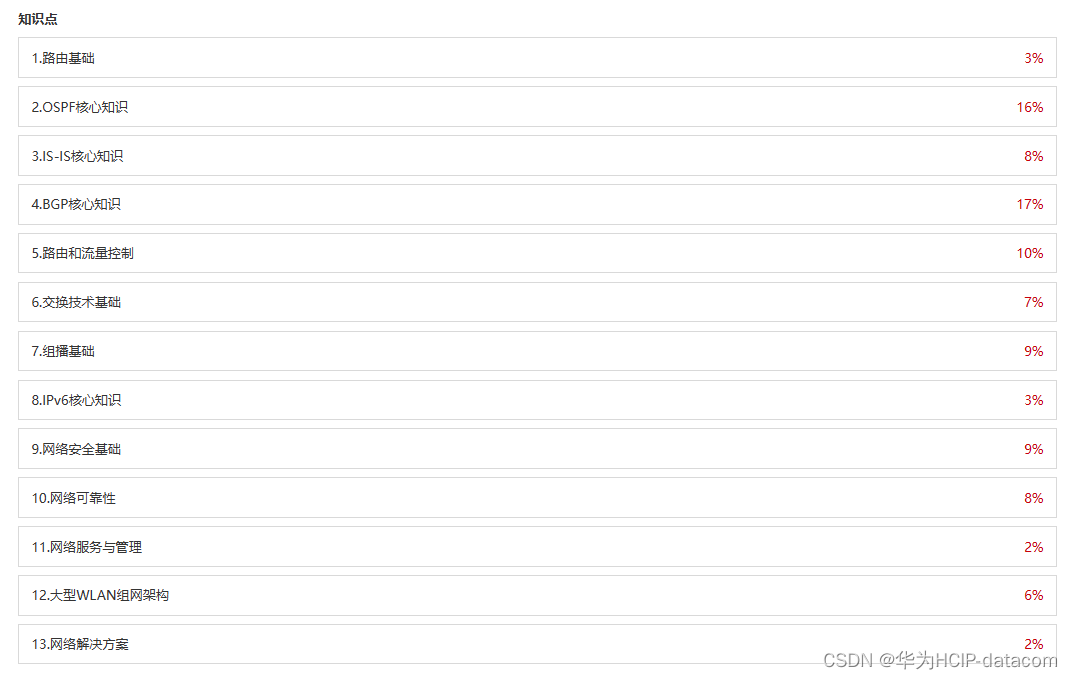
HCIP-datacom-821题库真题和机构资料
HCIP-Datacom-Core Technology考试内容 HCIP-Datacom-Core Technology V1.0考试覆盖数据通信领域各场景通用核心知识,包括路由基础、OSPF、IS-IS、BGP、路由和流量控制、以太网交换技术、组播、IPv6、网络安全、网络可靠性、网络服务与管理、WLAN、网络解决方案。 机…...

javaSE,javaEE,javaME的区别
1. JavaSE(Java Platform,Standard Edition,又称J2SE),可以理解为Java标准版本 这个版本的jdk通常包含了Java日常开发使用的基本类,允许开发和部署在桌面、服务器、嵌入式环境和实时环境中中使用࿰…...

mysql innodb一些知识点
1、事务和锁的关系; 在MySQL事务中,只要开始了一次事务,就会自动加上一个共享锁(Shared Lock)。这个锁会在事务结束时自动释放。如果在事务中需要更新某个数据对象,那么MySQL会将该数据对象的共享锁升级为…...

Android 面试题 应用对内存是如何限制 八
🔥 OutOfMemeryError的原因 🔥 Android 针对每个应用有内存限制 , 当JVM因为没有足够的内存来为对象分配空间并且垃圾回收器也已经没有空间可回收时,就会抛出这个error(注:非exception,因为这个问题已经严…...

赛车游戏——【极品飞车】(内含源码inscode在线运行)
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★前端炫酷代码分享 ★ ★ uniapp-从构建到提升★ ★ 从0到英雄,vue成神之路★ ★ 解决算法,一个专栏就够了★ ★ 架…...
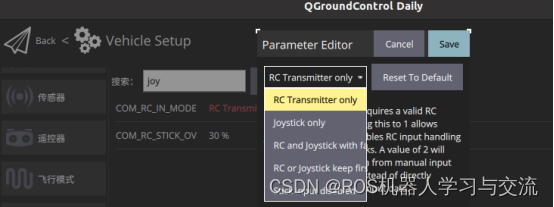
无人机调试笔记——常见参数
无人机的PID调试以及速度相关参数 1、Multicopter Position Control主要是用来设置无人机的各种速度和位置参数。调试顺序是先调试内环PID,也就是无人机的速度闭环控制,确认没有问题后再进行外环位置控制,也就是定点模式控制。 2、调试的时…...

如何快速实现多人协同编辑?
引言 协同编辑是目前成熟的在线文档编辑软件必备的功能,比如腾讯文档就支持多人协同编辑,基本都是采用监听command,然后同步此command给其他客户端来实现的,例如以下系列: https://gcdn.grapecity.com.cn/showtopic-…...
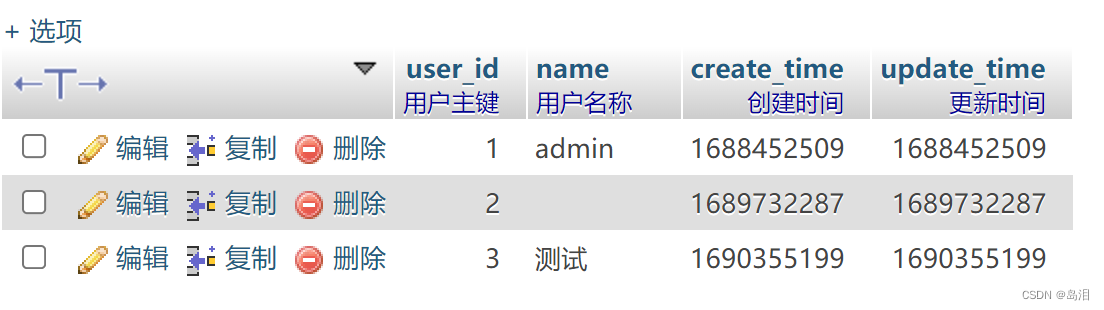
ThinkPHP 一对多关联
用一对多关联的前提 多的一方的数据库表有一的一方数据库表的外键。 举例,用户获取自己的所有文章 数据表结构如下 // 用户表 useruser_id - integer // 用户主键name - varchar // 用户名称// 文章表 articlearticle_id - integer // 文章主键title - varchar …...
基本数组及示例)
C++基础篇(二)基本数组及示例
目录 一、一维数组1、定义和初始化2、访问和修改3、元素逆置和冒泡排序 二、二维数组(用指针进行访问与修改)1、定义和初始化2、访问与修改 三、更高维度的数组1、三维数组2、高维数组 一、一维数组 1、定义和初始化 在 C 中,可以使用下面的…...

C++多态练习题
目录 一.习题1: 解决下列测试代码所出现的问题 测试用例1: 测试用例2: 代码改进: 习题1总结: 二.习题2. 求类对象的大小 三.习题3: 代码解析 : 解析图: 四.习题4ÿ…...

ELD透明屏在智能家居中有哪些优点展示?
ELD透明屏是一种新型的显示技术,它能够在不需要背光的情况下显示图像和文字。 ELD透明屏的原理是利用电致发光效应,通过在透明基板上涂覆一层特殊的发光材料,当电流通过时,发光材料会发出光线,从而实现显示效果。 ELD…...
第十三章 利用PCA简化数据
文章目录 第十三章 利用PCA简化数据13.1降维技术13.2PCA13.2.1移动坐标轴 13.2.2在NumPy中实现PCA13.3利用PCA对半导体制造数据降维 第十三章 利用PCA简化数据 PCA(Principal Component Analysis,主成分分析)是一种常用的降维技术࿰…...

开源中文分词Ansj的简单使用
ANSJ是由孙健(ansjsun)开源的一个中文分词器,为ICTLAS的Java版本,也采用了Bigram HMM分词模型:在Bigram分词的基础上,识别未登录词,以提高分词准确度。 虽然基本分词原理与ICTLAS的一样&#…...

251_多线程_创建一个多线程的图像处理应用,其中每个线程负责对一部分图像进行处理,然后将处理后的结果合并为最终图像
举一个更丰富的例子来说明多线程的用法。 我们将创建一个多线程的图像处理应用,其中每个线程负责对一部分图像进行处理,然后将处理后的结果合并为最终图像。 这个例子可以更好地展示多线程并发处理的优势。 假设有一个函数 processImageSection,它会对图像的一个特定区域进…...

[吐槽Edge浏览器]关于Edge浏览器的闪退问题
这个浏览器嘛,在谷歌浏览器不能页面翻译后,一直是用的高高兴兴的,可突然有一天,Edge浏览器页面加载不出来了。 很慌,大概就是页面崩溃、加载失败什么的都出现过。 修了整整一天,不知道原因在哪,…...

数据包在网络中传输的过程
ref: 【先把这个视频看完了】:数据包的传输过程【网络常识10】_哔哩哔哩_bilibili 常识都看看 》Ref: 1. 这个写的嘎嘎好,解释了为啥4层7层5层,还有数据包封装的问题:数据包在网络中的传输过程详解_数据包传输_张孟浩_jay的博客…...

Acwing.875 快速幂
题目 给定n组ai , bi, pi,对于每组数据,求出akimod pi的值。 输入格式 第一行包含整数n。 接下来n行,每行包含三个整数ai , bi,pi。输出格式 对于每组数据,输出一个结果,表示aibimod pi的值。 每个结果占一行。 数…...
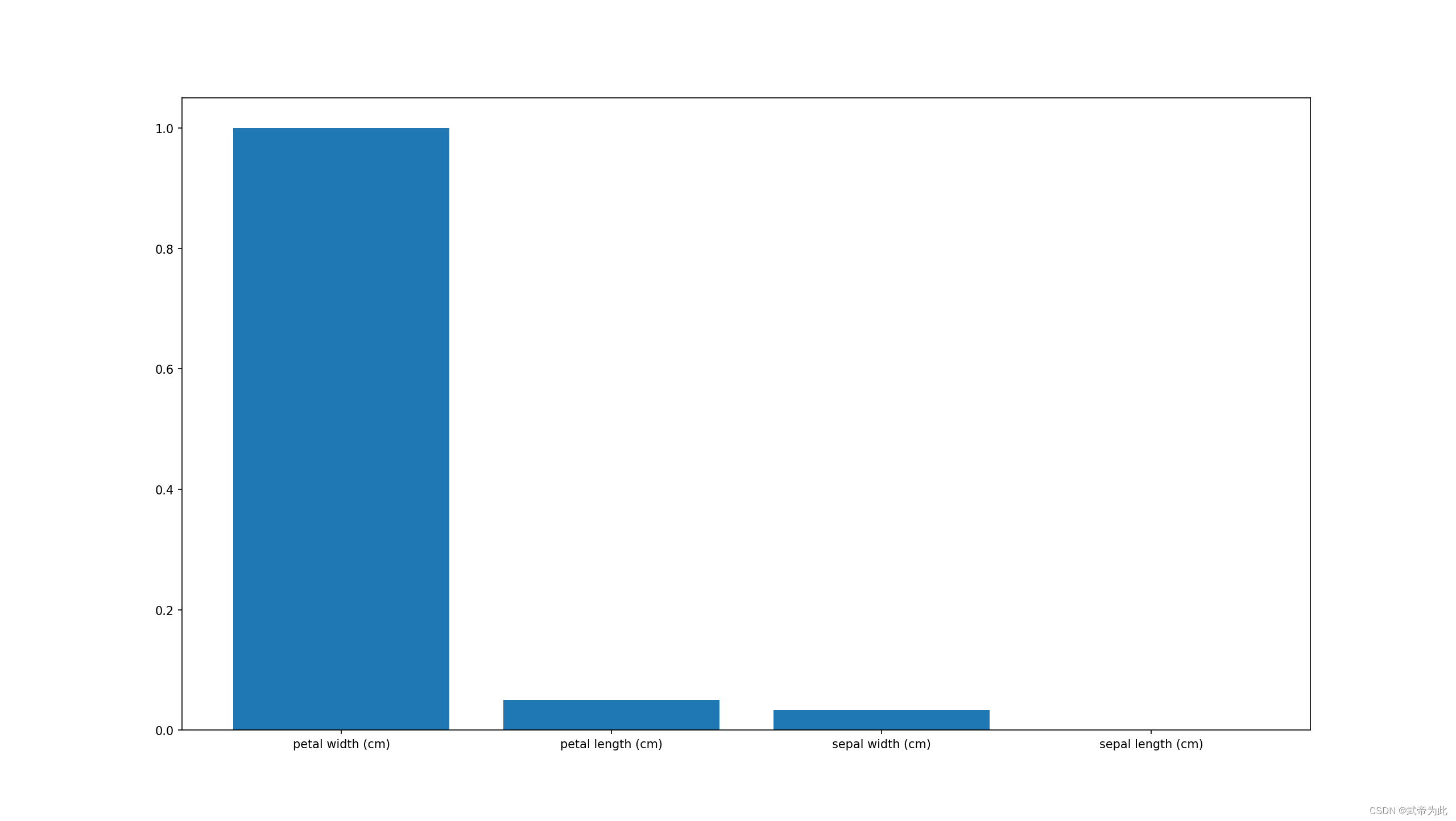
【决策树-鸢尾花分类】
决策树算法简介 决策树是一种基于树状结构的分类与回归算法。它通过对数据集进行递归分割,将样本划分为多个类别或者回归值。决策树算法的核心思想是通过构建树来对数据进行划分,从而实现对未知样本的预测。 决策树的构建过程 决策树的构建过程包括以…...
)
类与对象(中--构造函数)
类与对象(中--构造函数) 1、构造函数的特性2、默认构造函数3、编译器自动生成的默认构造函数(无参的)(当我们不写构造函数时)3.1 编译器自动生成的默认构造函数只对 自定义类型的成员变量 起作用࿰…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
