c刷题(一)
目录
1.输出100以内3的倍数
2.将3个数从大到小输出
3.打印100~200素数
方法一
方法二
4.显示printf的返回值
最大公约数
试除法
辗转相除法
九九乘法表
求十个数的最大值
1.输出100以内3的倍数
法一:
int n = 0;
while (n*3 < 100){printf("%d ", n*3);n++;}法二:
int i = 0;for (i = 1; i <= 100; i++) {if (i % 3 == 0){printf("%d ", i);}}2.将3个数从大到小输出
由于只有3个数,我们可以采用中间变量换值的方法,相比于依次判断就显得很简单了。
int a = 0;int b = 0;int c = 0;int tmp = 0;scanf("%d %d %d", &a, &b, &c);if (a < c){tmp = c;c = a;a = tmp;}if (a < b){tmp = b;b = a;a = tmp;}if (b < c){tmp = b;b = c;c = tmp;}printf("%d %d %d\n", a, b, c);return 0;
}需要注意的是,这种办法改变了原变量的值。
3.打印100~200素数
方法一
素数,也称质数,特点是只能被1和自身整除,那我们是不是可以用2~n-1之间的数依次来取模进行判断呢?如果有一个数能被整除,那它就不是质数,反之是质数。
int i = 101;int n;for (i = 101; i < 200; i++){int flag = 0;//开关for (n = 2; n < i; n++){if (i % n == 0){flag = 0;break;}else flag = 1;}if(flag == 1)printf("%d ", i); }因为其中一个数不能整除并不代表它不是素数,所以我们设置一个开关,依次在真和假中切换,能整除为假,不能整除为真,遍历一遍后根据flag的值判断它是否为素数。

方法二
任意不是素数的数都可以分为 m*n的形式。
16 = 4*4
16 = 2*8
如果将这个数开平方,如果它不是素数,则在2~√n之间必定有个数使它的因子。
(例:√18 = 3(整形省略分数)
18 = 2*9 18 = 3*6 )
大家想想是不是这样的道理,这样做可以减少遍历的次数。
#include <stdio.h>
#include<math.h>
int main(){int i = 101;int n;for (i = 101; i < 200; i+2){int flag = 0;for (n = 2; n <= sqrt(i); n++){if (i % n == 0){flag = 0;break;}else flag = 1;}if(flag == 1)printf("%d ", i); }
return 0;
}注意因子可以等于√n,sqrt是用来求根号的函数,需要包含头文件math.h
因为偶数不可能是素数,我们可以跳过偶数部分只进行奇数的循环。
4.显示printf的返回值
要求:第一行输入printf的输出值,第二行输出printf的返回值。
int ret = printf("hello world!");printf("\n%d", ret);
//等价于int ret = printf("\n%d", printf("hello world!")); 
由此我们可以得出结论:printf返回值是字符的个数
最大公约数
试除法
我们找到两个数中较小的那个,用它依次递减,如果能被这两个数整除,那它就是最大公约数。
int a = 0, b = 0;scanf("%d %d", &a, &b);int ret = a > b ? b : a;while (a % ret || b % ret){ret--;}printf("%d\n", ret);辗转相除法
具体来说就是两个数先求模,如果不等于0,被除数作为下一个除数,它们的模为新的被除数继续直到没有余数为止。
例如:24%12 = 0,则12就是最大公约数。25%12 = 1,12%1 = 0,1就是最大公约数。
反过来12%24 = 12,24%12 = 0,方法仍成立。
int a = 0, b = 0;int r = 0;scanf("%d %d", &a, &b);while (r = a % b){a = b;b = r;}printf("%d\n", b); 
附加题:如果要求最小公倍数该怎么做呢?
这里有个公式:最小公倍数 = 两数之积除以最大公约数(a*b/r)
九九乘法表
int i = 0;for (i = 1; i <= 9; i++){//打印一行int j = 0;for (j=1; j<=i; j++)//列数不超过行数{printf("%d*%d=%-2d ", i, j, i * j);}printf("\n");}
不多赘述,注意我们这里采用左对齐%-2d的方式,使得代码整齐,希望大家写代码的时候也能用到这样的技巧。
求十个数的最大值
这个没什么好说的,假定一个变量max遍历数组,选出最大值即可。需要注意的是,max只能是数组内的一个值,如果给它初始值为0,遇到负数可能会出现错误。
int arr[] = { -1,-2,-3,-4,-5,-6,-7,-8,-9,-10 };int max = arr[0];int i = 0;for (i = 1; i < 10; i++)//从第二个数开始{if (arr[i] > max)max = arr[i];}printf("%d\n", max);相关文章:

c刷题(一)
目录 1.输出100以内3的倍数 2.将3个数从大到小输出 3.打印100~200素数 方法一 方法二 4.显示printf的返回值 最大公约数 试除法 辗转相除法 九九乘法表 求十个数的最大值 1.输出100以内3的倍数 法一: int n 0; while (n*3 < 100){printf("%d &q…...

webpack
文章目录 webpack概念打包的场景为什么要打包在打包之外 - 翻译在打包之外 - 小动作 课程重点模块化利用立即执行函数来改变 作用域模块化的优点模块化方案的进化史AMD(成型比较早,应用不是很广泛)COMMONJSES6 MODULE webpack 的打包机制webp…...

反复 Failed to connect to github.com port 443 after xxx ms
前提:使用了代理,浏览器能稳定访问github,但git clone一直超时 解决方案: 1. git config --global http.proxy http://127.0.0.1:1080 2. 代理设置端口1080 3. 1080可自定义 感谢来自这篇博客和评论区的提醒:解决…...

ARM裸机-11
1、安装交叉编译工具工具 1.1、windows中装软件的特点 windows中装软件使用安装包,安装包解压后有两种情况:一种是一个安装文件 (.exe/.msi),双击进行安装,下一步直到安装完毕。安装完毕后会在桌面上生成快捷方式,我们平时使用快…...

centos7升级glibc
作者:吴业亮 博客:wuyeliang.blog.csdn.net 安装bison: yum install bison -y安装wget、bzip2、gcc、gcc-c和glibc-headers: yum -y install wget bzip2 gcc gcc-c glibc-headers安装make-4.2.1: wget http://ftp.…...

【OnnxRuntime】在linux下编译并安装C++版本的onnx-runtime
目录 安装C接口的onnx-runtime安装依赖项:下载源文件构建ONNX Runtime安装ONNX Runtime 安装C接口的onnx-runtime 安装依赖项: 安装CMake:可以通过包管理器(如apt、yum等)安装CMake。 安装C编译器:确保系…...
 的 fftshift, ifftshift 函数的实现)
C#基于OpenCv(OpenCvSharp) 的 fftshift, ifftshift 函数的实现
本文实现基于OpenCv(OpenCvSharp) 的 fftshift, ifftshift 函数。 fftshift 函数将信号频谱的零频分量移动到数组中心, 本质是分别对调一三象限数据。 ifftshift完成相反的操作,本质是二四象限的数据块。 OpenCV中没有这两个函数如果使用需要自己实现。 实现代码如下: …...
【SpringBoot】笔记2
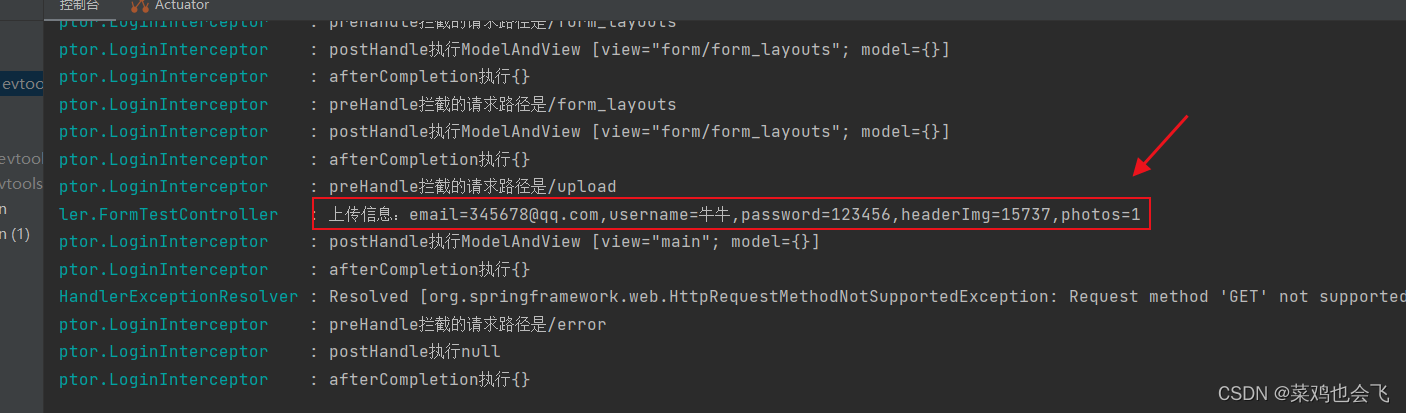
文章目录 45、web实验-抽取公共页面46、web实验-遍历数据与页面bug修改47、视图解析-【源码分析】-视图解析器与视图[暂时没看]48、拦截器-登录检查与静态资源放行49、拦截器-【源码分析】-拦截器的执行时机和原理50、文件上传-单文件与多文件上传的使用51、文件上传-【源码流程…...
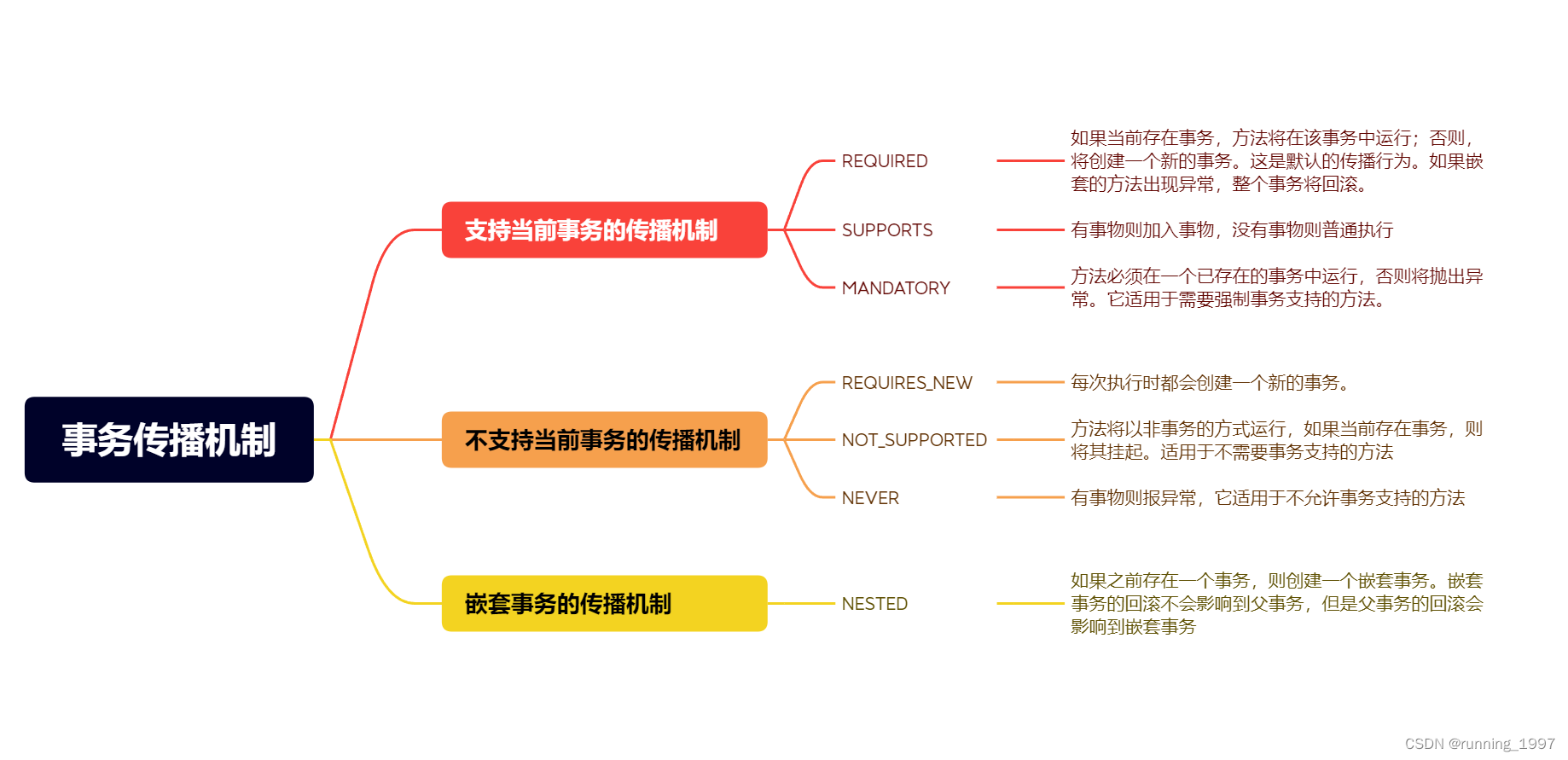
Spring事务传播机制详细讲解
文章目录 一、事务传播机制1. REQUIRED:2. SUPPORTS:3. MANDATORY:4. REQUIRES_NEW:5. NOT_SUPPORTED:6. NEVER:7. NESTED: 二、事务传播机制分类1. 支持当前事务的传播机制:REQUIRE…...
kubernetes 集群搭建(kubeadm 方式)
目前生产部署 Kubernetes 集群主要有两种方式: (1) kubeadm Kubeadm 是一个 Kubernetes 官方提供的命令行工具,可以用来部署和管理 Kubernetes 集群。它主要用于在新的 Kubernetes 环境中初始化集群、添加或删除节点等操作。 K…...
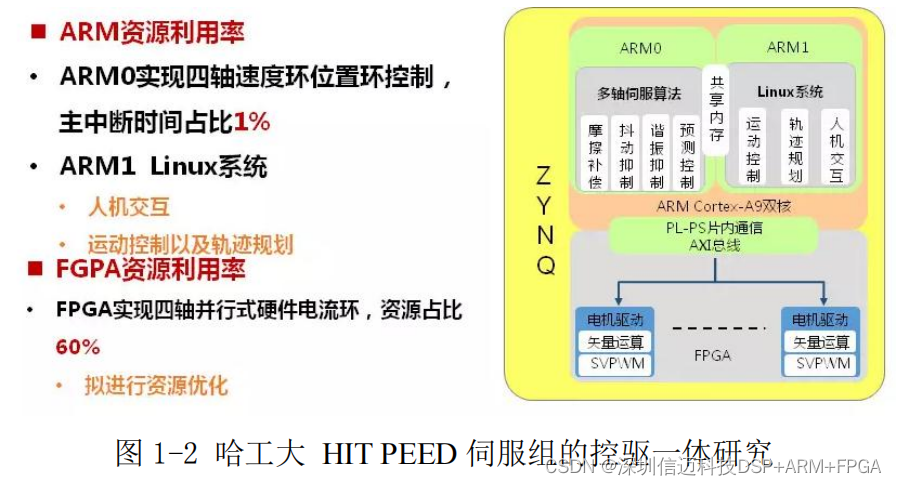
基于ARM+FPGA的驱控一体机器人控制器设计
目前市场上工业机器人,数控机床等多轴运动控制系统普遍采用运动控制器加 伺服驱动器的分布式控制方式。在这种控制方式中,控制器一方面完成人机交互,另 一方面进行 NC 代码的解释执行,插补运算,继而将计算出来的位…...
docker 安装 字体文件
先说一下我当前的 场景 及 环境,这样同学们可以先评估本篇文章是否有帮助。 环境: dockerphp8.1-fpmwindows 场景: 来了个需求,有一个默认背景图,可以理解为背景图是一个 "相框",相框里面就会放…...

Vue.js与ASP.NET的结合,实现企业级应用的开发和部署
在当今快速发展的互联网技术领域,企业级应用的开发和部署变得越来越重要。Vue.js和ASP.NET是两个在前端和后端开发中广泛使用的技术,将它们结合起来可以为企业级应用的开发和部署带来诸多优势。本文将通过代码示例介绍如何使用Vue.js和ASP.NET进行企业级…...
Uncaught SyntaxError: ‘‘ string literal contains an unescaped line break
今天在修改前端页面的时候,页面报错了,提示了这个信息 Uncaught SyntaxError: string literal contains an unescaped line break 问题指向这行代码,这就是通过JS渲染一个easyui的搜索框,仔细确认之后,发现没有任何问…...

Vue3+Vite+TypeScript常用项目模块详解
目录 1.Vue3ViteTypeScript 概述 1.1 vue3 1.1.1 Vue3 概述 1.1.2 vue3的现状与发展趋势 1.2 Vite 1.2.1 现实问题 1.2 搭建vite项目 1.3 TypeScript 1.3.1 TypeScript 定义 1.3.2 TypeScript 基本数据类型 1.3.3 TypeScript语法简单介绍 2. 项目配置简单概述 2.…...

数字电路(一)
1、例题 1、进行DA数模转换器选型时,一般要选择主要参数有( A)、转换精度和转换速度。 A、分辨率 B、输出电流 C、输出电阻 D、模拟开关 2、下图所示电路的逻辑功能为( B) A、与门 B、或门 C、与非门 D、或非门 分析该…...

Oracle也有回收站
在数据库管理中,数据的删除是一个常见的操作。然而,有时候我们可能会意外地删除了一些重要的数据。幸运的是,Oracle数据库提供了一个类似于回收站的功能,可以帮助我们恢复被删除的数据。本文将介绍Oracle数据库中的回收站功能以及…...
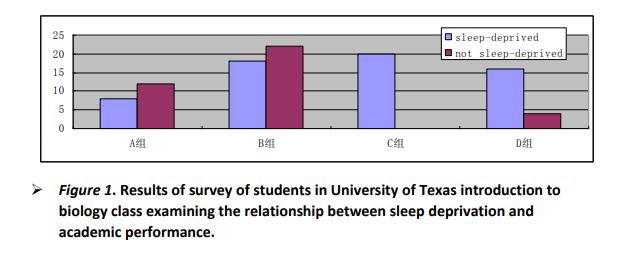
投稿注意!APA格式超全示例详解,原本28天能录用,可能要拖延2个月
为什么同一本期刊有论文28天录用,有论文10个月才录用?结合近期征稿的这本经管类SSCI期刊,小编(Unionpub学术)整理了部分影响录用的几个因素,准备提交此期刊的作者可自查参考下: (参…...
【Python】Web学习笔记_flask(1)——模拟登录
安装flask pip3 install flask 第一部分内容: 1、主页面输出hello world 2、根据不同用户名参数输出用户信息 3、模拟登录 from flask import Flask,url_for,redirectappFlask(__name__)app.route(/) def index():return hello worldapp.route(/user/<uname…...

css单行文本省略号多行文本省略号
设置单行文本省略号的写法 : 先设置宽固定的宽度 :width: 300px; 设置不换行 :white-space:nowrap; 设置省略号:text-overflow: ellipsis; 裁剪多余的内容/溢出的内容:overflow: hidden; width: 200px; white-space:…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
