当前位置： 首页 > news >正文

C#基于OpenCv（OpenCvSharp） 的 fftshift, ifftshift 函数的实现

news 2026/2/10 19:48:08

本文实现基于OpenCv（OpenCvSharp） 的 fftshift, ifftshift 函数。

fftshift 函数将信号频谱的零频分量移动到数组中心, 本质是分别对调一三象限数据。

ifftshift完成相反的操作，本质是二四象限的数据块。

OpenCV中没有这两个函数如果使用需要自己实现。

实现代码如下：

#region 方法 fftshift/// <summary>/// 方法 fftshift/// </summary>/// <param name="src"></param>/// <returns></returns>public static Mat fftshift(Mat src){Mat dst = new Mat(src.Size(), src.Type());int x0 = src.Cols / 2;int x1 = src.Cols - x0;int y0 = src

相关文章：

C#基于OpenCv（OpenCvSharp） 的 fftshift, ifftshift 函数的实现

本文实现基于OpenCv（OpenCvSharp） 的 fftshift, ifftshift 函数。 fftshift 函数将信号频谱的零频分量移动到数组中心, 本质是分别对调一三象限数据。 ifftshift完成相反的操作，本质是二四象限的数据块。 OpenCV中没有这两个函数如果使用需要自己实现。 实现代码如下： …...

编程日记 2023/8/1 15:03:42

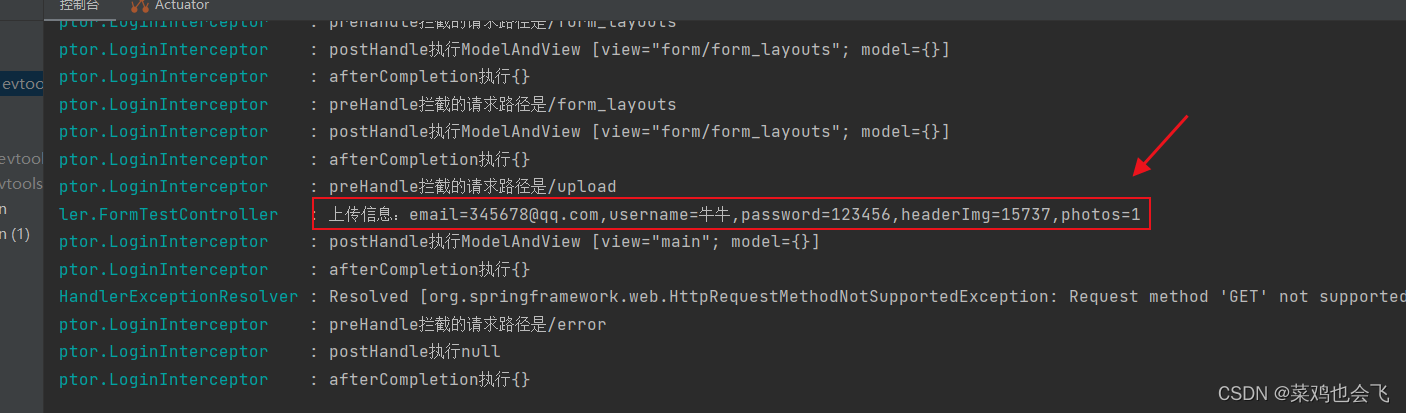
【SpringBoot】笔记2

文章目录 45、web实验-抽取公共页面46、web实验-遍历数据与页面bug修改47、视图解析-【源码分析】-视图解析器与视图[暂时没看]48、拦截器-登录检查与静态资源放行49、拦截器-【源码分析】-拦截器的执行时机和原理50、文件上传-单文件与多文件上传的使用51、文件上传-【源码流程…...

编程日记 2023/8/1 15:02:41

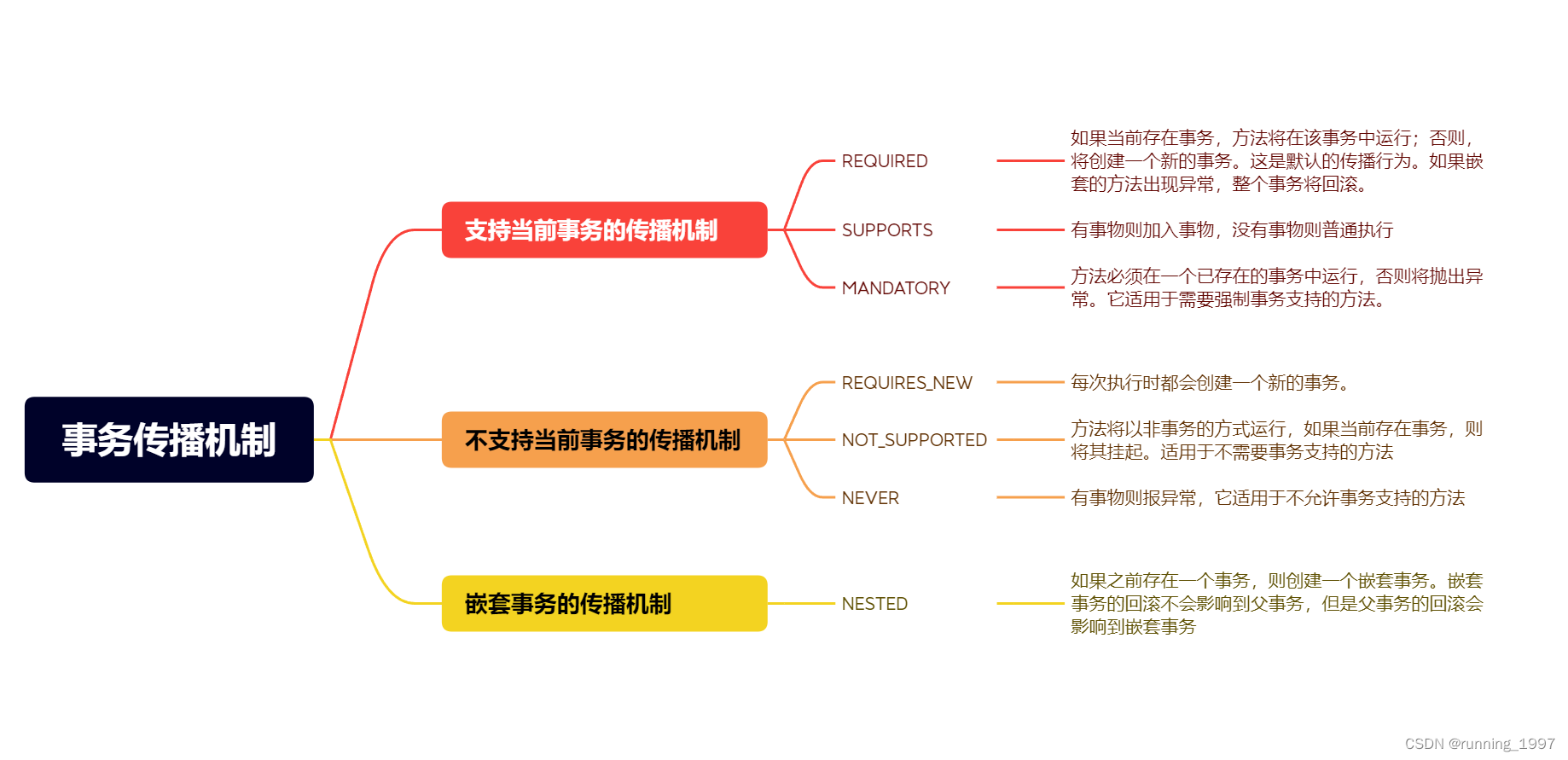
Spring事务传播机制详细讲解

文章目录 一、事务传播机制1. REQUIRED&#xff1a;2. SUPPORTS&#xff1a;3. MANDATORY&#xff1a;4. REQUIRES_NEW&#xff1a;5. NOT_SUPPORTED&#xff1a;6. NEVER&#xff1a;7. NESTED&#xff1a; 二、事务传播机制分类1. 支持当前事务的传播机制&#xff1a;REQUIRE…...

编程日记 2023/8/1 15:01:39

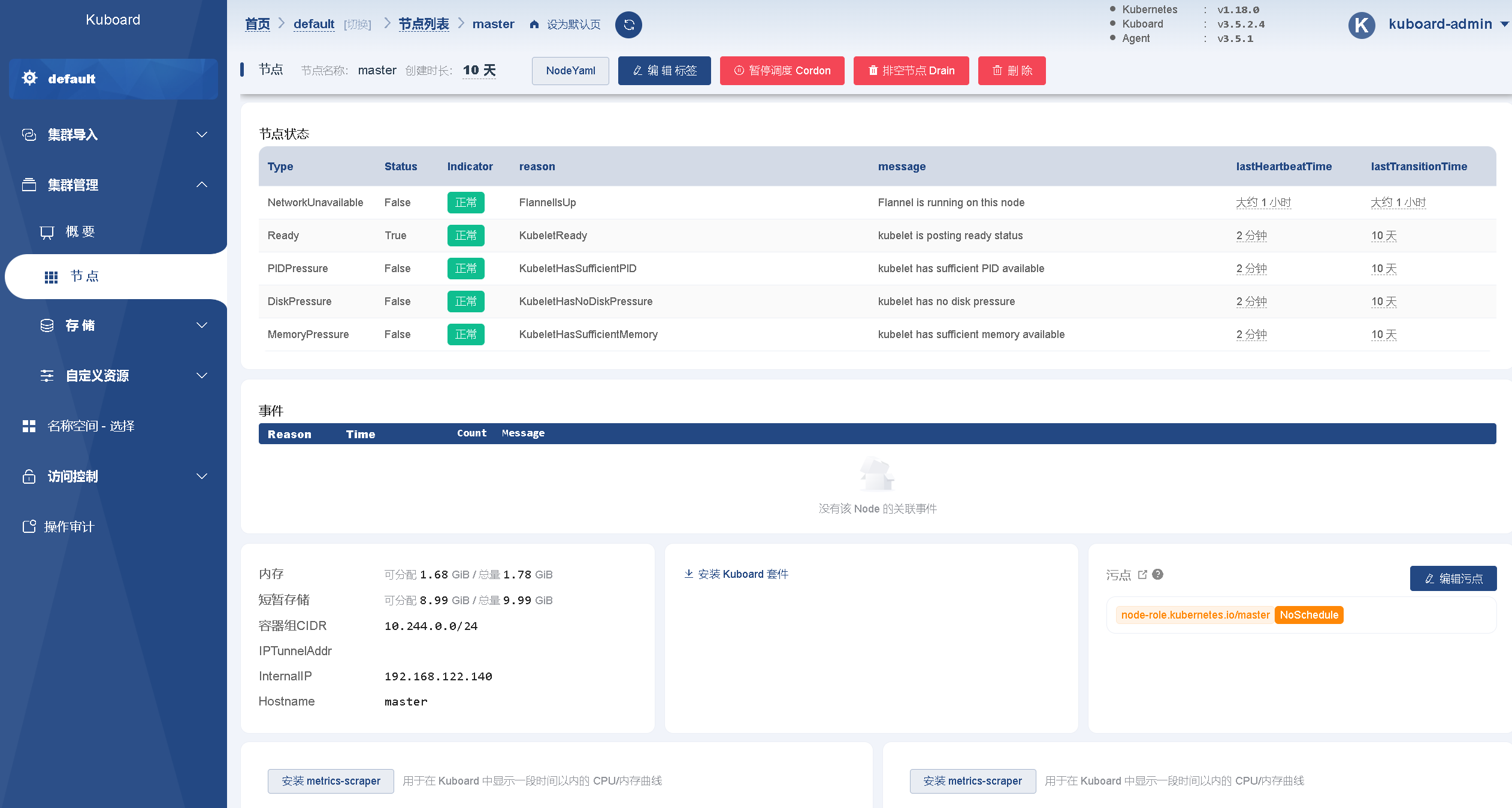
kubernetes 集群搭建(kubeadm 方式)

目前生产部署 Kubernetes 集群主要有两种方式&#xff1a; &#xff08;1&#xff09; kubeadm Kubeadm 是一个 Kubernetes 官方提供的命令行工具&#xff0c;可以用来部署和管理 Kubernetes 集群。它主要用于在新的 Kubernetes 环境中初始化集群、添加或删除节点等操作。 K…...

编程日记 2023/8/1 15:00:38

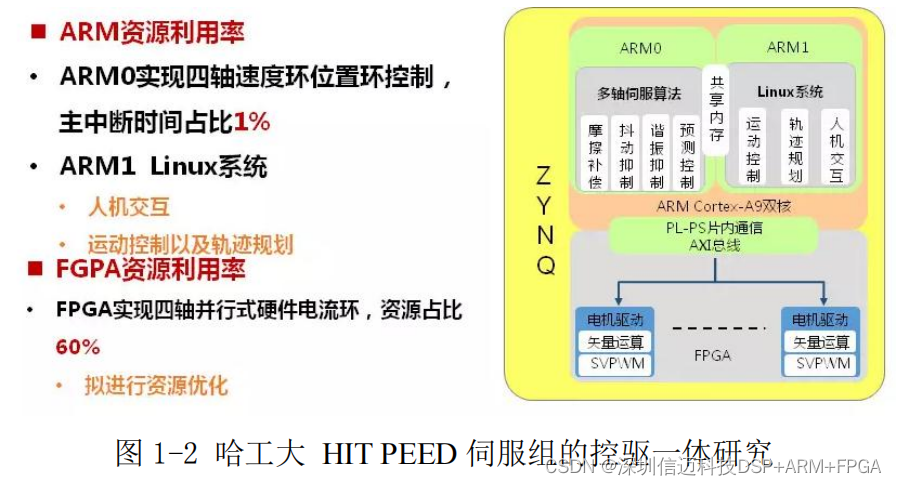
基于ARM+FPGA的驱控一体机器人控制器设计

目前市场上工业机器人&#xff0c;数控机床等多轴运动控制系统普遍采用运动控制器加 伺服驱动器的分布式控制方式。在这种控制方式中&#xff0c;控制器一方面完成人机交互&#xff0c;另 一方面进行 NC 代码的解释执行&#xff0c;插补运算&#xff0c;继而将计算出来的位…...

编程日记 2023/8/1 14:59:36

docker 安装 字体文件

先说一下我当前的 场景 及 环境&#xff0c;这样同学们可以先评估本篇文章是否有帮助。 环境&#xff1a; dockerphp8.1-fpmwindows 场景&#xff1a; 来了个需求&#xff0c;有一个默认背景图&#xff0c;可以理解为背景图是一个 "相框"&#xff0c;相框里面就会放…...

编程日记 2023/8/1 14:58:35

Vue.js与ASP.NET的结合，实现企业级应用的开发和部署

在当今快速发展的互联网技术领域&#xff0c;企业级应用的开发和部署变得越来越重要。Vue.js和ASP.NET是两个在前端和后端开发中广泛使用的技术&#xff0c;将它们结合起来可以为企业级应用的开发和部署带来诸多优势。本文将通过代码示例介绍如何使用Vue.js和ASP.NET进行企业级…...

编程日记 2023/8/1 14:57:34

Uncaught SyntaxError: ‘‘ string literal contains an unescaped line break

今天在修改前端页面的时候&#xff0c;页面报错了&#xff0c;提示了这个信息 Uncaught SyntaxError: string literal contains an unescaped line break 问题指向这行代码&#xff0c;这就是通过JS渲染一个easyui的搜索框&#xff0c;仔细确认之后&#xff0c;发现没有任何问…...

编程日记 2023/8/1 14:56:32

Vue3+Vite+TypeScript常用项目模块详解

目录 1.Vue3ViteTypeScript 概述 1.1 vue3 1.1.1 Vue3 概述 1.1.2 vue3的现状与发展趋势 1.2 Vite 1.2.1 现实问题 1.2 搭建vite项目 1.3 TypeScript 1.3.1 TypeScript 定义 1.3.2 TypeScript 基本数据类型 1.3.3 TypeScript语法简单介绍 2. 项目配置简单概述 2.…...

编程日记 2023/8/1 14:55:31

数字电路(一)

1、例题 1、进行DA数模转换器选型时&#xff0c;一般要选择主要参数有&#xff08; A&#xff09;、转换精度和转换速度。 A、分辨率 B、输出电流 C、输出电阻 D、模拟开关 2、下图所示电路的逻辑功能为&#xff08; B&#xff09; A、与门 B、或门 C、与非门 D、或非门 分析该…...

编程日记 2023/8/1 14:54:29

Oracle也有回收站

在数据库管理中&#xff0c;数据的删除是一个常见的操作。然而&#xff0c;有时候我们可能会意外地删除了一些重要的数据。幸运的是&#xff0c;Oracle数据库提供了一个类似于回收站的功能&#xff0c;可以帮助我们恢复被删除的数据。本文将介绍Oracle数据库中的回收站功能以及…...

编程日记 2023/8/1 14:53:28

投稿注意！APA格式超全示例详解，原本28天能录用，可能要拖延2个月

为什么同一本期刊有论文28天录用&#xff0c;有论文10个月才录用&#xff1f;结合近期征稿的这本经管类SSCI期刊&#xff0c;小编&#xff08;Unionpub学术&#xff09;整理了部分影响录用的几个因素&#xff0c;准备提交此期刊的作者可自查参考下&#xff1a; &#xff08;参…...

编程日记 2023/8/1 14:52:26

【Python】Web学习笔记_flask(1)——模拟登录

安装flask pip3 install flask 第一部分内容&#xff1a; 1、主页面输出hello world 2、根据不同用户名参数输出用户信息 3、模拟登录 from flask import Flask,url_for,redirectappFlask(__name__)app.route(/) def index():return hello worldapp.route(/user/<uname…...

编程日记 2023/8/1 14:51:26

css单行文本省略号多行文本省略号

设置单行文本省略号的写法 &#xff1a; 先设置宽固定的宽度 &#xff1a;width: 300px; 设置不换行 &#xff1a;white-space:nowrap; 设置省略号&#xff1a;text-overflow: ellipsis; 裁剪多余的内容/溢出的内容&#xff1a;overflow: hidden; width: 200px; white-space:…...

编程日记 2023/8/1 14:50:24

信号槽中的函数重载

信号槽中的函数重载 QT4的方式QT5的方式函数指针重载函数QT5信号函数重载解决方案 总结 QT4的方式 Qt4中声明槽函数必须要使用 slots 关键字, 不能省略。 信号函数&#xff1a; 槽函数&#xff1a; mainwondow: cpp文件&#xff1a; #include "mainwindow.h"…...

编程日记 2023/8/1 14:49:22

计算机视觉（五）深度学习基础

文章目录 深度学习基础卷积神经网络与传统神经网络区别深度学习与神经网络的区别 目标函数选择合适的目标函数Softmax层 改进的梯度下降梯度消失的直观解释激活函数学习步长SGD的问题Momentum动量Nesterov MomentumAdagradRMSpropAdam 各种梯度下降算法比较关于算法选择的建议B…...

编程日记 2023/8/1 14:48:22

ES6学习-Generator

Generator 种异步编程解决方案 函数会返回一个遍历器对象语法上:Generator 函数是一个状态机&#xff0c;封装了多个内部状态。形式上:Generator 函数是一个普通函数;有两个特征。一是&#xff0c;function关键字与函数名之间有一个星号&#xff1b;二是&#xff0c;函数体内部…...

编程日记 2023/8/1 14:47:21

Flowable-服务-微服务任务

目录 定义图形标记XML内容界面操作 定义 Sc 任务不是 BPMN 2.0 规范定义的官方任务&#xff0c;在 Flowable 中&#xff0c;Sc 任务是作为一种特殊的服务 任务来实现的&#xff0c;主要调用springcloud的微服务使用。 图形标记 由于 Sc 任务不是 BPMN 2.0 规范的“官方”任务…...

编程日记 2023/8/1 14:46:19

opencv03-补充-vector的操作

opencv03-补充-vector的操作 参考&#xff1a;https://www.runoob.com/w3cnote/cpp-vector-container-analysis.html 构造方法(具体介绍看API文档) class Student {public:private:string name;};int main() {vector<int>();vector<int> v1;vector<Student&g…...

编程日记 2023/8/1 14:45:17

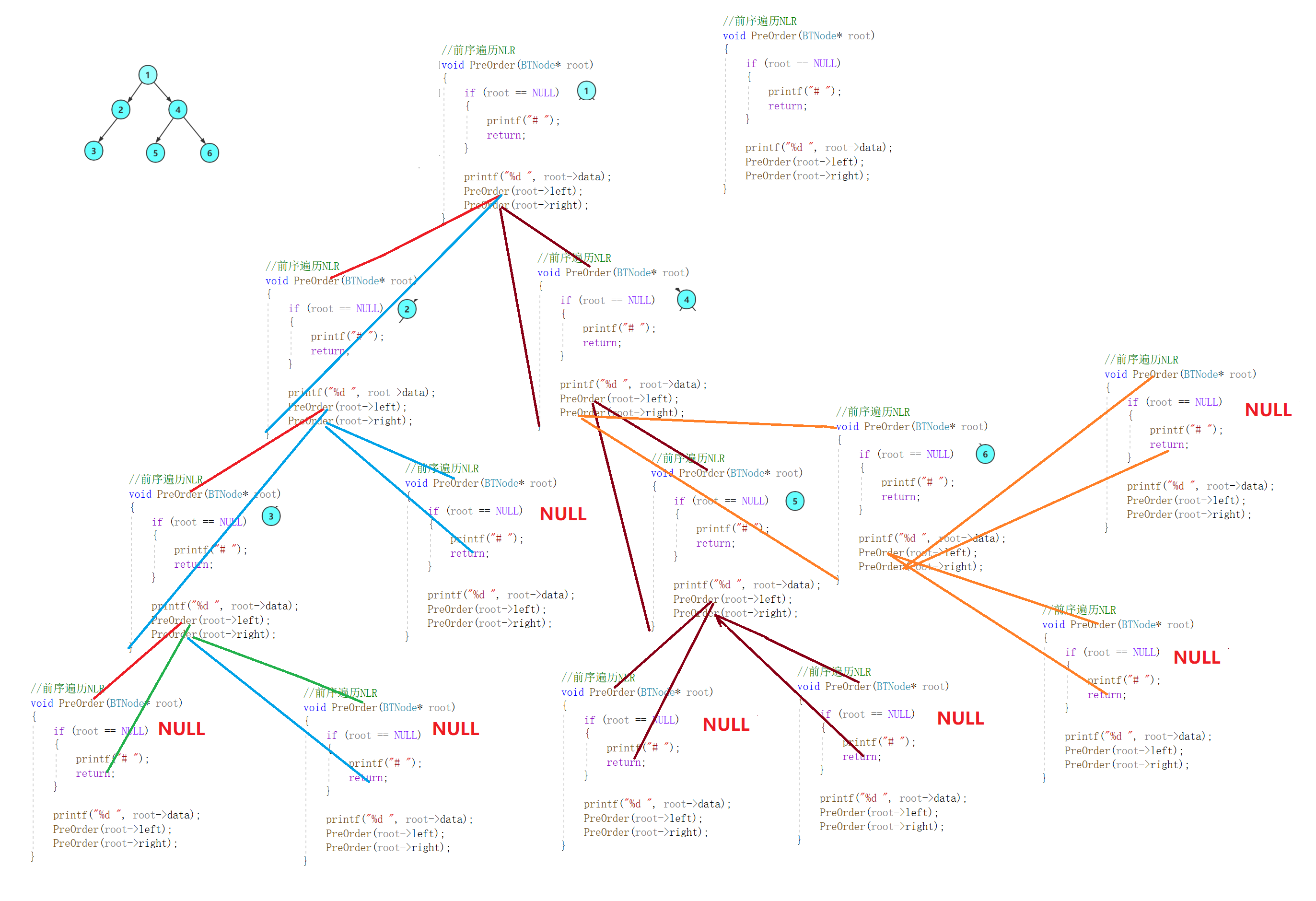
二叉树(C语言)

文章目录 1.树1.1概念1.2相关定义1.3 表示&#xff08;左孩子右兄弟&#xff09; 2.二叉树2.1概念2.2特殊的二叉树1. 满二叉树&#xff1a;2. 完全二叉树&#xff1a; 2.3二叉树的性质2.4练习 3.二叉树的存储结构1. 顺序存储2. 链式存储 4.完全二叉树的代码实现4.1堆的介绍1.堆…...

编程日记 2023/8/1 14:44:16

java_网络服务相关_gateway_nacos_feign区别联系

1. spring-cloud-starter-gateway 作用&#xff1a;作为微服务架构的网关&#xff0c;统一入口&#xff0c;处理所有外部请求。 核心能力&#xff1a; 路由转发&#xff08;基于路径、服务名等&#xff09;过滤器&#xff08;鉴权、限流、日志、Header 处理&#xff09;支持负…...

编程新知 2025/11/28 2:51:33

rknn优化教程（二）

文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK&#xff0c;开始写第二篇的内容了。这篇博客主要能写一下&#xff1a; 如何给一些三方库按照xmake方式进行封装&#xff0c;供调用如何按…...

编程新知 2025/6/11 15:25:30

【Oracle APEX开发小技巧12】

有如下需求&#xff1a; 有一个问题反馈页面&#xff0c;要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据&#xff0c;方便管理员及时处理反馈。 我的方法&#xff1a;直接将逻辑写在SQL中&#xff0c;这样可以直接在页面展示 完整代码&#xff1a; SELECTSF.FE…...

编程新知 2026/2/7 17:35:15

DIY｜Mac 搭建 ESP-IDF 开发环境及编译小智 AI

前一阵子在百度 AI 开发者大会上&#xff0c;看到基于小智 AI DIY 玩具的演示&#xff0c;感觉有点意思&#xff0c;想着自己也来试试。 如果只是想烧录现成的固件&#xff0c;乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外&#xff0c;还提供了基于网页版的 ESP LA…...

编程新知 2026/2/3 8:13:35

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用

1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

编程新知 2025/10/3 17:30:30

用docker来安装部署freeswitch记录

今天刚才测试一个callcenter的项目&#xff0c;所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

编程新知 2026/2/1 3:20:44

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

基于IDIG-GAN的小样本电机轴承故障诊断

目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) ​梯度归一化（Gradient Normalization）​​ (2) ​判别器梯度间隙正则化（Discriminator Gradient Gap Regularization）​​ (3) ​自注意力机制（Self-Attention）​​ 3. 完整损失函数 二…...

编程新知 2026/1/31 10:58:46

R 语言科研绘图第 55 期 --- 网络图-聚类

在发表科研论文的过程中&#xff0c;科研绘图是必不可少的&#xff0c;一张好看的图形会是文章很大的加分项。 为了便于使用&#xff0c;本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中&#xff0c;获取方式&#xff1a; R 语言科研绘图模板 --- sciRplothttps://mp.…...

编程新知 2026/1/30 2:34:31

C++_哈希表

本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、基础概念 1. 哈希核心思想&#xff1a; 哈希函数的作用&#xff1a;通过此函数建立一个Key与存储位置之间的映射关系。理想目标&#xff1a;实现…...

编程新知 2026/1/28 11:27:52