Acwing.873.欧拉函数
题目
给定n个正整数ai,请你求出每个数的欧拉函数。

输入格式
第一行包含整数n。
接下来n行,每行包含一个正整数ai。
输出格式
输出共n行,每行输出一个正整数an的欧拉函数。
数据范围
1 ≤n ≤100
1≤ai≤2* 109
- 输入样例:
3
3
6
8
- 输出样例:
2
2
4
题解
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{int n;cin >> n;while (n -- ){int a;cin >> a;int res = a;for (int i = 2; i <= a / i; i ++)if (a % i -= o)l{res = res / i*(i - 1);while (a % i == 0) a /= i;}if (a > 1) res = res / a * ( a - 1);cout << res << endl;
}
return 0;思路
欧拉函数公式由容斥定理推导,具体图下图



相关文章:

Acwing.873.欧拉函数
题目 给定n个正整数ai,请你求出每个数的欧拉函数。 输入格式 第一行包含整数n。 接下来n行,每行包含一个正整数ai。 输出格式 输出共n行,每行输出一个正整数an的欧拉函数。 数据范围 1 ≤n ≤100 1≤ai≤2* 109 输入样例: 3 3 6 8输…...
深入浅出FPGA——笔记7 代码风格
1 寄存器电路的设计方式 废话:时序逻辑设计是核心,而寄存器又是时序逻辑的基础。 1: 简单的时序输入输出模型 如下图所示,在每个时钟信号clk的有效沿(通常是上升沿),输入端数据din将被锁存到输出端dout。…...

npm, yarn配置
一、npm 1. 查看当前的镜像源。 npm config get registry 2. 设置为淘宝源 npm config set registry https://registry.npm.taobao.org 3. 还原默认源 npm config set registry https://registry.npmjs.org/ 二、Yarn 1.yarn的安装 npm install -g yarn 2. 查看当…...

跨域情况下,vue如何下载后台接口提供的application/octet-stream文件流Excel文件
前言 由于跨域,所以无法直接通过window.location.href或者a标签直接下载,直接拼后台接口地址又暴露了后台地址,不可行。 所以在这种跨域情况下,本章讲一下vue如何下载后台接口提供的application/octet-stream文件流Excel文件。 …...
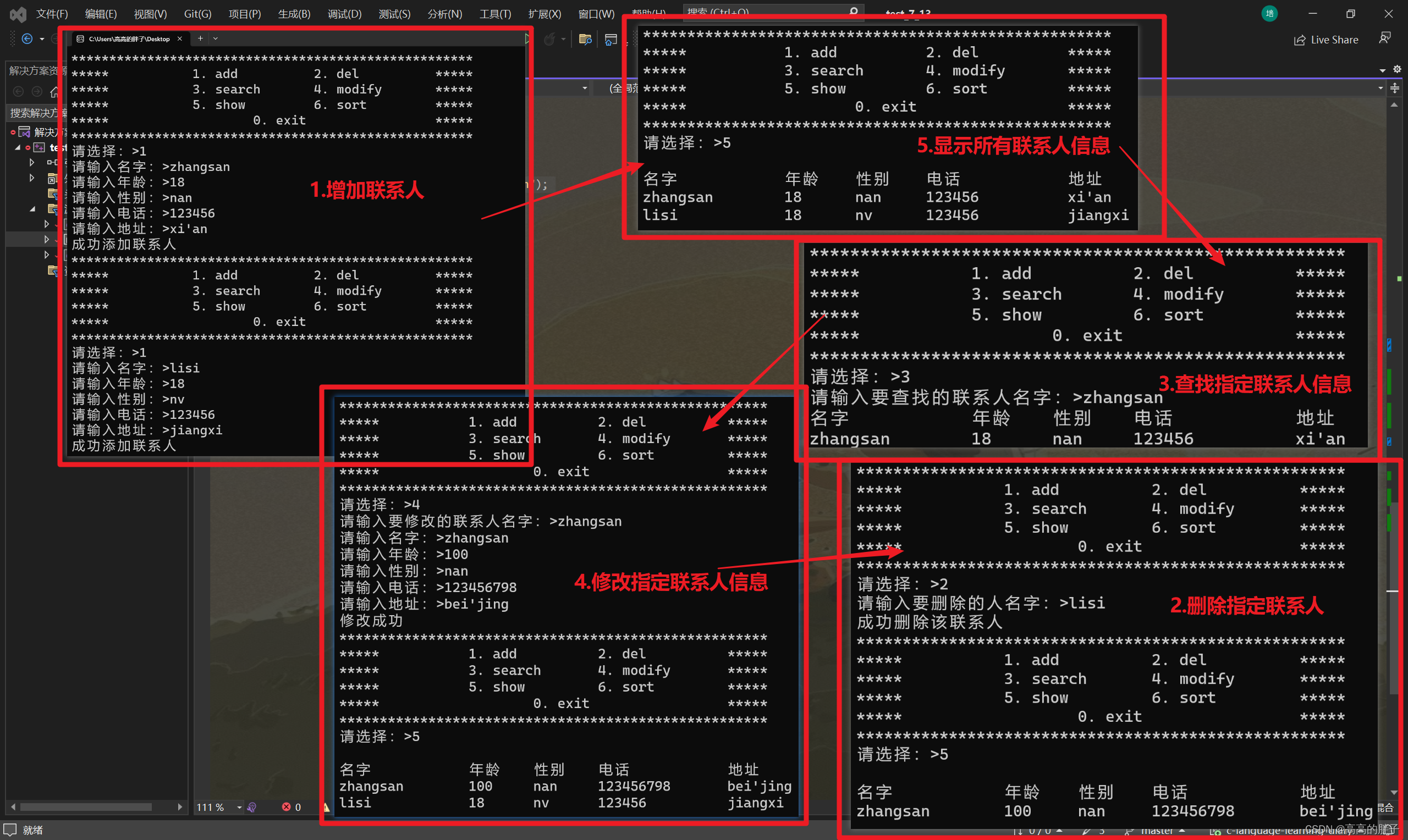
学C的第三十一天【通讯录的实现】
相关代码gitee自取:C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十天【自定义类型:结构体、枚举、联合】_高高的胖子的博客-CSDN博客 通讯录需求: 实现一个通讯录, 通讯录中存放保存人的信息࿱…...
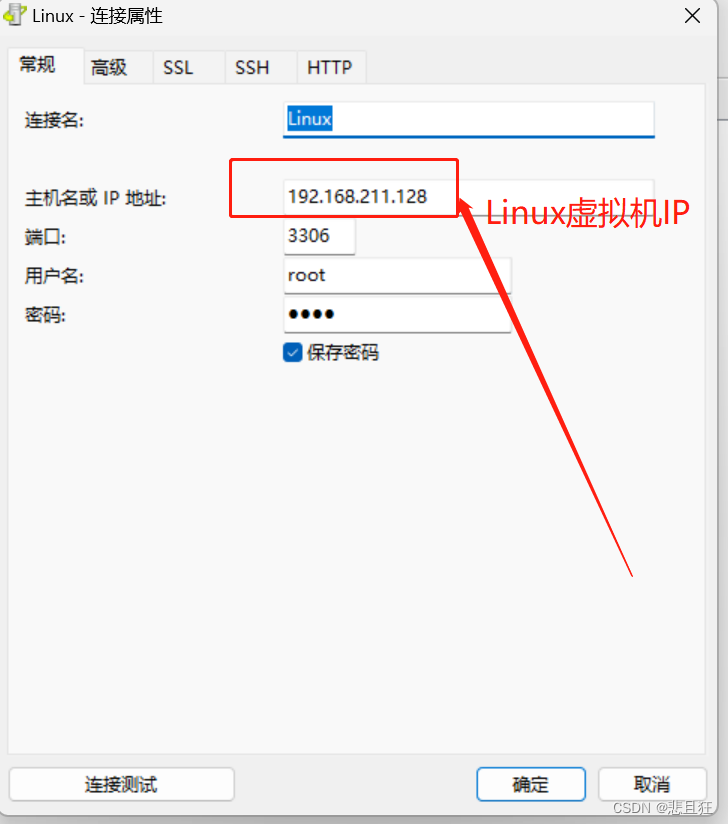
Linux操作系统学习,Linux基础命令大全
目录 第一章、Linux简介和安装1.1)Linux简介和分类1.2)安装VMware虚拟机,在虚拟机中安装CentOS 7 第二章、虚拟机中Linux的IP地址配置详解2.1)什么是IP地址,如何查看2.2)虚拟机NAT模式中Linux的IP地址设置有…...

【软件测试】说说你对TDD测试驱动开发的理解?
很多公司在面测试中高级岗时,都会不同程度地问到“有没有了解过TDD”“你认为TDD可以解决什么问题”或者“说说测试驱动开发的流程”等等,即使公司并不会用到此开发流程,面试官也会通过你对这个相对还比较“陌生”的概念的讲述来了解你对一些…...

B. Binary Cafe(二进制的妙用)
题目:Problem - B - Codeforces 总结: 对于该题最简单的方法为使用二进制的数表示状态 例如: 对于一个数7的二进制:111 它的每一位都可表示两种状态我们可以理解为取或者不取 对于7这个数字它可以表示一种状态即在三个位置都…...
SpringBoot单元测试
目录 1.什么是单元测试? 2.单元测试有哪些好处? 3.Spring Boot单元测试使⽤ 单元测试的实现步骤 1. ⽣成单元测试类 2. 添加单元测试代码 2.1 .添加Spring Boot框架测试注解:SpringBootTest 2.2 添加单元测试业务逻辑 简单的断⾔说明 1.什么是单元测试? 单元测试(un…...

刷题 41-45
四十一、移除元素 示例 1: 输入:nums [3,2,2,3], val 3 输出:2, nums [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 …...

Centos时间同步
前言 在 Linux 操作系统中,正确的时间同步是非常重要的,因为它对于很多应用程序都是必需的。本文将介绍两种在 Centos 系统中同步当前时间的方式。 方法一:使用 ntpdate 命令同步当前时间 ntpdate 命令是一种简单快捷的同步当前时间的方式&a…...
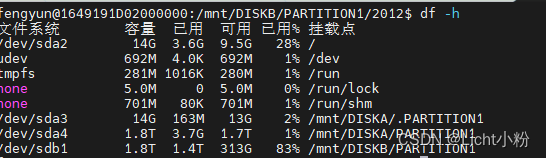
Linux 查看磁盘空间
1 查看当前目录的总大小 :du -sh ps:du(disk usage) 2 查看某个目录的总大小:du -sh 目录名 3 查找出/目录下占用空间最大的前10个文件或者文件夹:sudo du -a / | sort -n -r | head -n 10 4 查看磁盘信息:df -h...
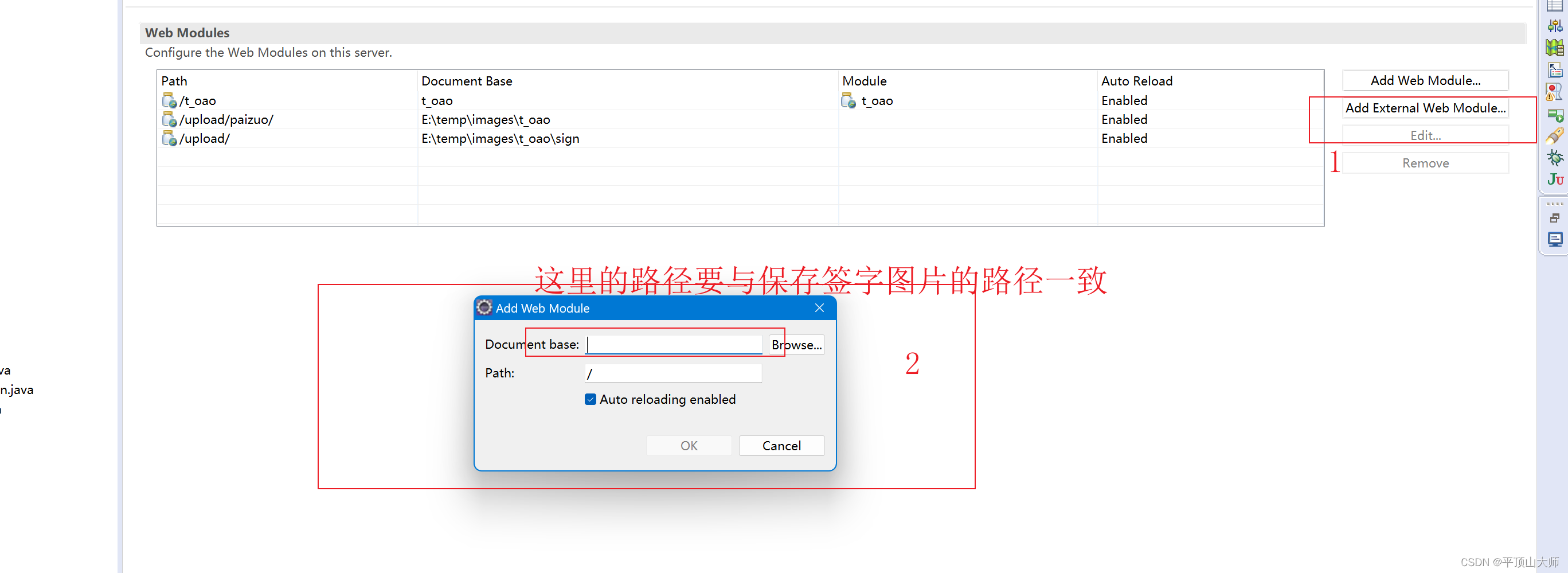
我的会议(我的审批,会议签字附源码)
目录 前言: 3.我的审批: 3.1实现的特色功能: 3.2显示的效果 3.3思路: 3.4寻找相关的案例或者自己使用JavaScript去写一个类似的功能 3.5具体的步骤: 3.5.1添加静态的jsp代码(我的审批数据的显示&…...

Python 装饰器该如何理解?
哈喽大家好,今天带大家了解下在Python中装饰器的使用 定义 首先我们先来了解下装饰器的定义。顾名思义,在Python中,装饰器本质上就是一个函数,它可以接收一个函数作为参数,然后返回一个新的函数。这个新的函数可以在…...
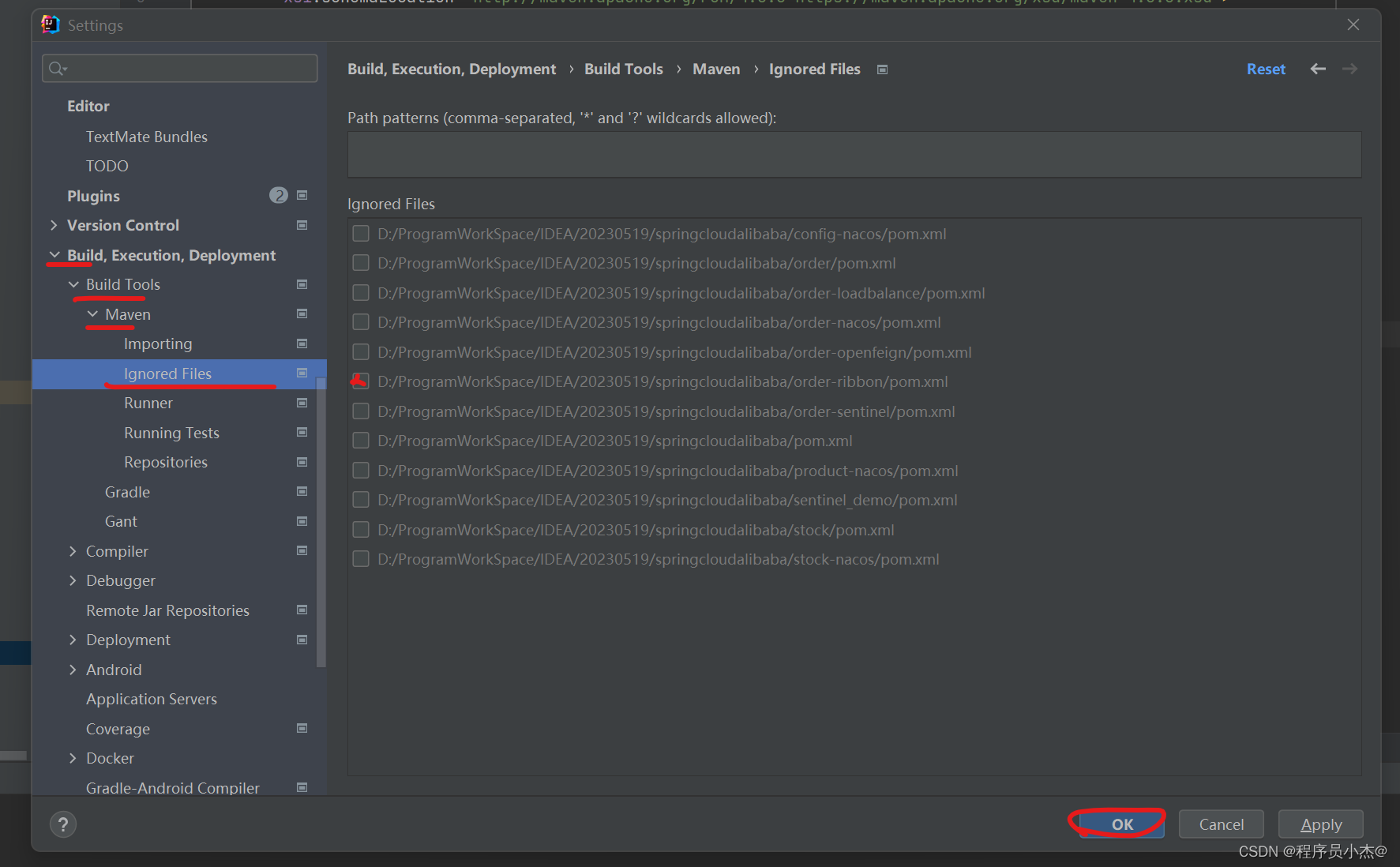
IDEA 模块不加载依旧是灰色 没有变成小蓝色的方块
Settings > Build, Execution, Deployment > Build Tools > Maven > Ignored Files下降对应的模块勾选掉 但通常在Maven的配置中,您会找到一个名为“ignoredFiles”的列表,其中包含被忽略的文件和目录。您可以通过取消选中所需的文件或目录…...
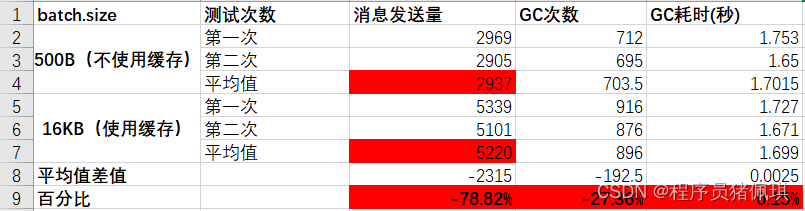
可以写进简历的kafka优化-----吞吐量提升一倍的方法
冲突 在看到项目工程里kafka 生产端配置的batch.size为500,而实际业务数据平均有1K大小的时候;我有点懵了。是的,这里矛盾了;莫非之前的作者认为这个batch.size是发送的条数,而不是kafka生产端内存缓存记录的大小&…...

JavaScript中,for in 和for of的区别
for in 遍历的是数组的索引(即键名),而 for of 遍历的是数组元素值(即键值)。for...in 循环出的是 key,for...of 循环出的是 value 推荐在循环对象属性的时候使用 for...in,在遍历数组的时候的时…...

计算机毕设 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

vue3 axios接口封装
在Vue 3中,可以通过封装axios来实现接口的统一管理和调用。封装后的接口调用更加简洁,代码可维护性也更好。以下是一个简单的Vue 3中axios接口封装的示例: 1.首先,安装axios和qs(如果需要处理复杂数据)&am…...

誉天程序员-2301-3-day08
4. 书籍管理实现CURD 这个结构比较复杂,是有一套复杂的机制,注意它们之间的关系和控制实现。 新增和修改怎么复用对话框 对话框中的数据,表格中展现的数据,临时记录正在操作的数据统一联动起来 单条删除怎么传递数据&am…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
