matlab使用教程(6)—线性方程组的求解
1mldivide 算法
2方阵方程组
2.1非奇异系数矩阵
A = pascal(3);
u = [3; 1; 4];
x = A\ub = magic(3);
X = A\b2.2奇异系数矩阵
P = pinv(A)*brank(A)pinv(A)*bA*pinv(A)*bA*pinv(A)*brref([A b])3超定方程组
t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';
B = table(t,y)E = [ones(size(t)) exp(-t)]c = E\yT = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')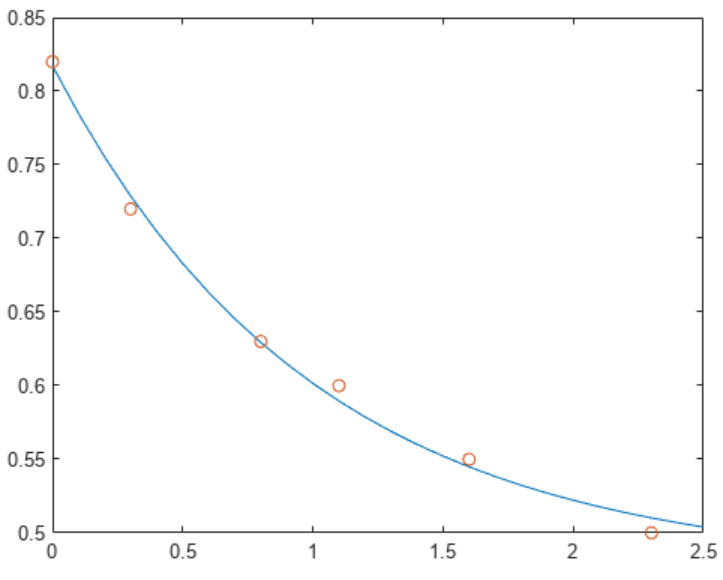
4欠定方程组
R = [6 8 7 3; 3 5 4 1]
rng(0);
b = randi(8,2,1)format rat
p = R\bZ = null(R,'r')
q = [-2; 1];
x = p + Z*q;
format short
norm(R*x - b)p = lsqminnorm(R,b)5多右端线性方程组的求解
[L,U] = lu(A);
x = U \ (L \ b);dA = decomposition(A,'lu');
x = dA\b;n = 1e3;
A = sprand(n,n,0.2) + speye(n);
b = ones(n,1);
% Backslash solution
tic
for k = 1:100
x = A\b;
end
toc% decomposition solution
tic
dA = decomposition(A);
for k = 1:100
x = dA\b;
end
toc6迭代法
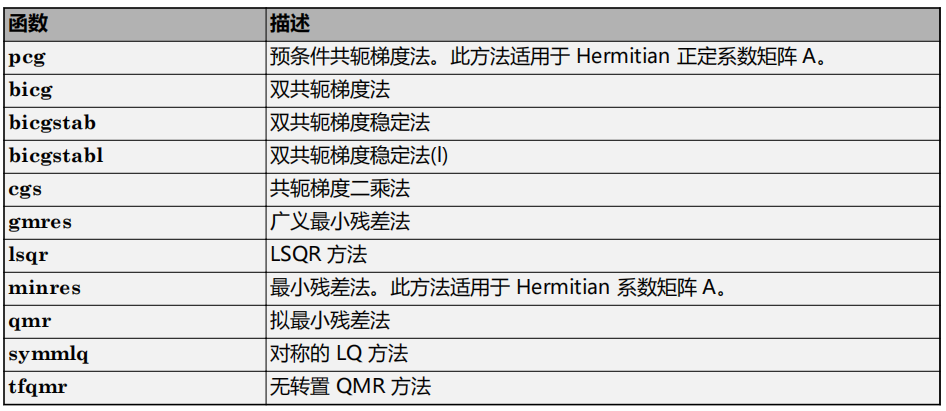
7多线程计算
相关文章:

matlab使用教程(6)—线性方程组的求解
进行科学计算时,最重要的一个问题是对联立线性方程组求解。在矩阵表示法中,常见问题采用以下形式:给定两个矩阵 A 和 b,是否存在一个唯一矩阵 x 使 Ax b 或 xA b? 考虑一维示例具有指导意义。例如,方程 …...

Verilog语法学习——边沿检测
边沿检测 代码 module edge_detection_p(input sys_clk,input sys_rst_n,input signal_in,output edge_detected );//存储上一个时钟周期的输入信号reg signal_in_prev;always (posedge sys_clk or negedge sys_rst_n) beginif(!sys_rst_n)signal_in_prev < 0;else…...

springboot和springcloud的联系与区别
什么是springboot? Spring Boot是一个用于简化Spring应用程序开发的框架,它提供了一种约定优于配置的方式,通过自动配置和快速开发能力,可以快速搭建独立运行、生产级别的Spring应用程序。 在传统的Spring应用程序开发中…...
【Web开发指南】如何用MyEclipse进行JavaScript开发?
由于MyEclipse中有高级语法高亮显示、智能内容辅助和准确验证等特性,进行JavaScript编码不再是一项繁琐的任务。 MyEclipse v2023.1.2离线版下载 JavaScript项目 在MyEclipse 2021及以后的版本中,大多数JavaScript支持都是开箱即用的JavaScript源代码…...

【C++进阶】多态
⭐博客主页:️CS semi主页 ⭐欢迎关注:点赞收藏留言 ⭐系列专栏:C进阶 ⭐代码仓库:C进阶 家人们更新不易,你们的点赞和关注对我而言十分重要,友友们麻烦多多点赞+关注,你们的支持是我…...
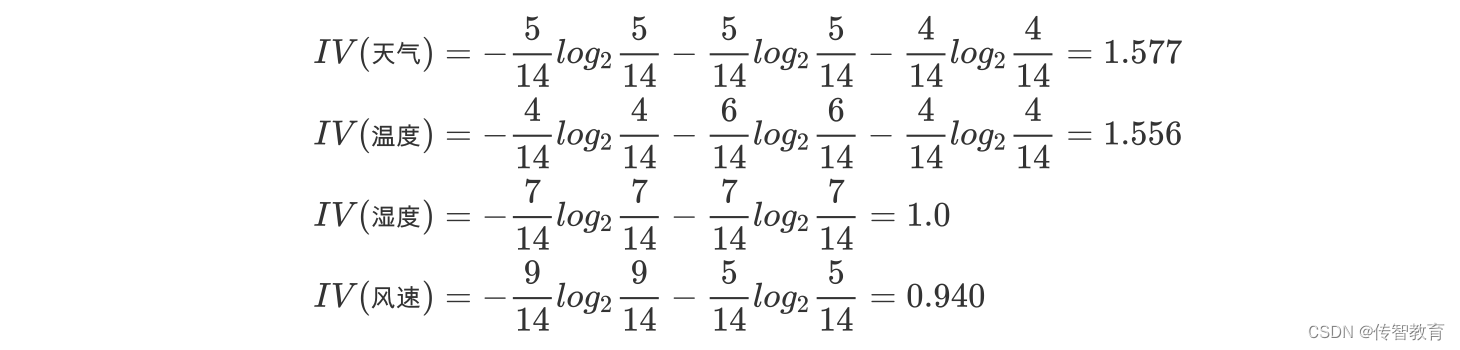
决策树的划分依据之:信息增益率
在上面的介绍中,我们有意忽略了"编号"这一列.若把"编号"也作为一个候选划分属性,则根据信息增益公式可计算出它的信息增益为 0.9182,远大于其他候选划分属性。 计算每个属性的信息熵过程中,我们发现,该属性的值为0, 也就…...

SolidUI社区-独立部署 和 Docker 通信分析
背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目,旨在将自然语言处理(NLP)与计算机图形学相…...
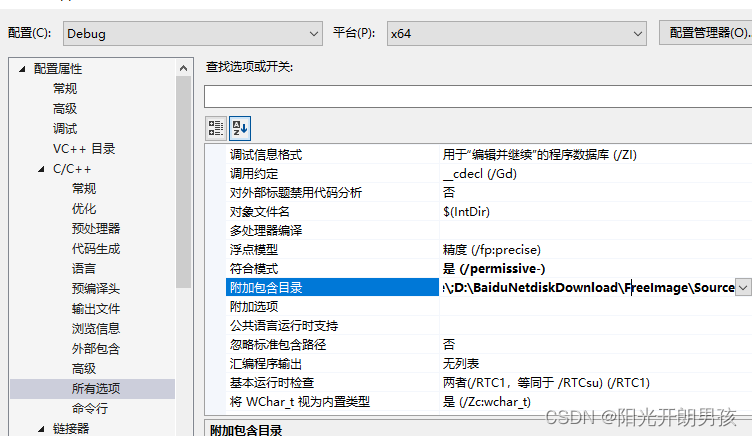
Windows下FreeImage库的配置
首先下载FreeImage库,http://freeimage.sourceforge.net/download.html,官网下载如下: 内部下载地址:https://download.csdn.net/download/qq_36314864/88140305 解压后,打开FreeImage.2017.sln,如果是vs…...
用python编写一个小程序,如何用python编写软件
大家好,给大家分享一下用python编写一个小程序,很多人还不知道这一点。下面详细解释一下。现在让我们来看看! 1、python可以写手机应用程序吗? 我想有人曲解意思了,人家说用python开发渣蔽一个手机app,不是…...

WPF实战学习笔记32-登录、注册服务添加
增加全局账户名同步 增加静态变量 添加文件:Mytodo.Common.Models.AppSession.cs ausing Prism.Mvvm; using System; using System.Collections.Generic; using System.ComponentModel; using System.Linq; using System.Text; using System.Threading.Tasks; us…...
XGBoost的参数
目录 1. 迭代过程 1.1 迭代次数/学习率/初始𝐻最大迭代值 1.1.1 参数num_boost_round & 参数eta 1.1.2 参数base_score 1.1.3 参数max_delta_step 1.2 xgboost的目标函数 1.2.1 gamma对模型的影响 1.2.2 lambda对模型的影响 2. XGBoost的弱评估器 2.…...
【已解决】windows7添加打印机报错:加载Tcp Mib库时的错误,无法加载标准TCP/IP端口的向导页
windows7 添加打印机的时候,输入完打印机的IP地址后,点击下一步,报错: 加载Tcp Mib库时的错误,无法加载标准TCP/IP端口的向导页 解决办法: 复制以下的代码到新建文本文档.txt中,然后修改文本文…...
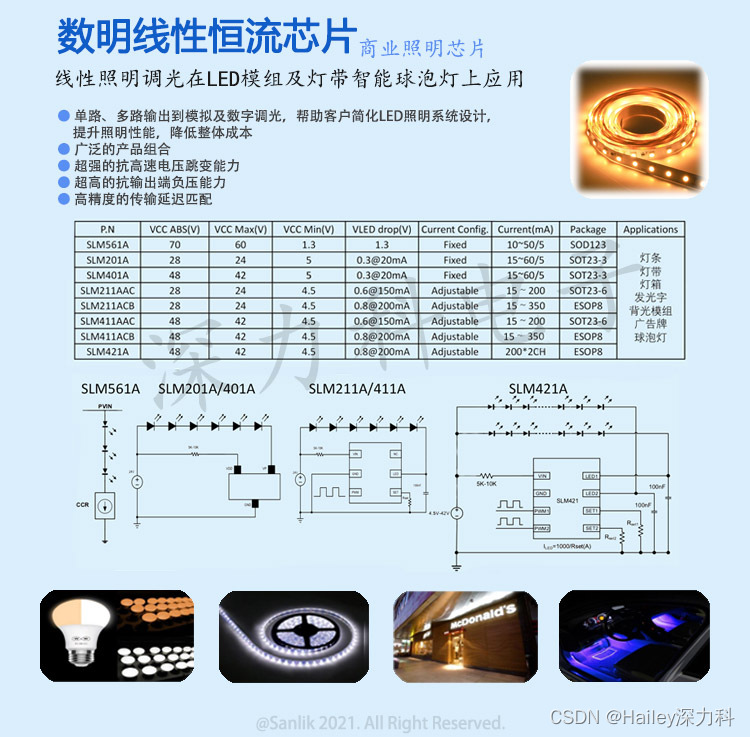
用于紫外线消毒灯的LED驱动:数明深紫外消毒方案SLM201
用于紫外线消毒灯的LED驱动SLM201 应用于紫外线消毒灯的LED驱动。疫情过后让越来越多的人开始注重起个人健康,除了出门佩戴口罩外,对于居家消毒也越发重视起来。而居家消毒除了75%浓度酒精及各类消毒液外,利用紫外线灯给衣物表面、房间消毒也…...
Docker部署Springboot应用【mysql部署+jar部署+Nginx部署】
【项目达到目标】 1.基本准备 2、mysql部署 3、jar部署 4、Nginx部署 一、基本准备 石工拿的就是之前放置在我们服务器上的应用进行部署,主要就是mysql和jar还有Vue的部署。 目前已经有的是jar、已经打包好的vue 二、mysql部署 docker run -d --name mysql \ …...
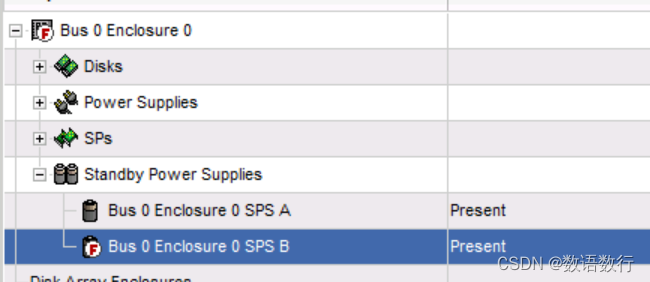
EMC VNX1系列存储电池状态说明
SPS电池正常的状态为“Present”。 SPS电池故障时的状态为“Faulted”。 更换SPS后,SPS开始充电,此时状态显示为“Not Ready”状态。 充电完成后显示为Present状态。如果充电完成后状态前面有“F”标记,则需要重启对应的控制器以更新SPS…...

pyspark 判断 Hive 表是否存在
Catalog.tableExists(tableName: str, dbName: Optional[str] None) → booltableName:表名 dbName:库名(可选) return:bool 值 spark SparkSession \.builder \.appName(tableExists) \.config(spark.num.executors, 6) \.config(spark.executor.memo…...

选择排序算法
选择排序 算法说明与代码实现: 以下是使用Go语言实现的选择排序算法示例代码: package mainimport "fmt"func selectionSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {minIndex : ifor j : i 1; j < n; j {if arr[j] < a…...
快速了解MyBatis---映射关系多对一
文章目录 映射关系多对一映射关系-官方文档映射关系多对1-基本介绍基本介绍注意细节 映射关系多对1-映射方式映射方式配置Mapper.xml 方式-应用实例注解实现多对1 映射-应用实例 映射关系多对一 映射关系-官方文档 文档地址: https://mybatis.org/mybatis-3/zh/sqlmap-xml.ht…...

python学到什么程度算入门,python从入门到精通好吗
本篇文章给大家谈谈python学到什么程度算入门,以及python从入门到精通好吗,希望对各位有所帮助,不要忘了收藏本站喔。 学习 Python 之 进阶学习 一切皆对象 1. 变量和函数皆对象2. 模块和类皆对象3. 对象的基本操作 (1). 可以赋值给变量(2). …...
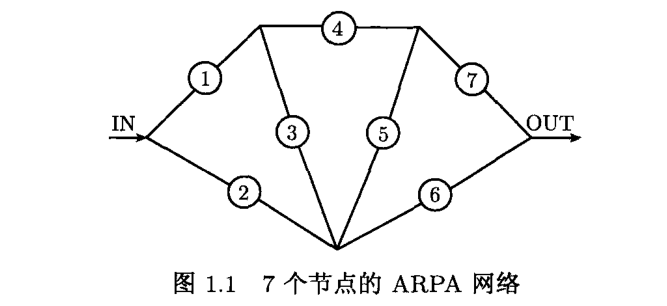
整数规划——第一章 引言
整数规划——第一章 引言 整数规划是带整数变量的最优化问题,即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。 考虑一个电视机工厂的生产…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
