一起来学算法(邻接矩阵)
前言:
邻接矩阵是数学和计算机科学中常用的一种表示方式,用来表述有向图或无向图,一张图由一组顶点(或结点)和一组表组成,用邻接矩阵就能表示这些顶点间存在的边的关系
1.图的概念
对于图而言,是数据结构中最复杂的结构,而是在做题的过程中,最大的难点在于BFS和DFS的过程,图从两个维度划分可以有:有向图、无权图、带权图。
1.有向图和无向图:
在无向图中,边没有方向,表示的是双向关系,换句话来说,如果两个顶点(或结点)之间存在边,那么这两个顶点就互相连接
例如,如果你正在建模一个社交网络,你可能会使用无向图,因为友谊是双向,如果1是2的朋友,那么2也是1的朋友,如图示:

有向图:与无向图相反,有向图的边有方向,表示单向关系,在这种图中,如果存在从1到2的边,那不一定存在从2到1的边,如图所示:

2.无权图和带权图
在图论中,图可以是无权的也可以是带权的,这主要取决于边是否具有与其关联的值(权重)
无权图:
在无权图中,边没有权重,或者说所有边的权重都是相同的,你只关心两个节点(顶点)之间是否存在边,而不是关心边的长度或者是成本,比如,社交网络的人际关心就可以用无权图来表示,如果两个人是朋友,就有一条边连接它们,所有的边都被视为相等
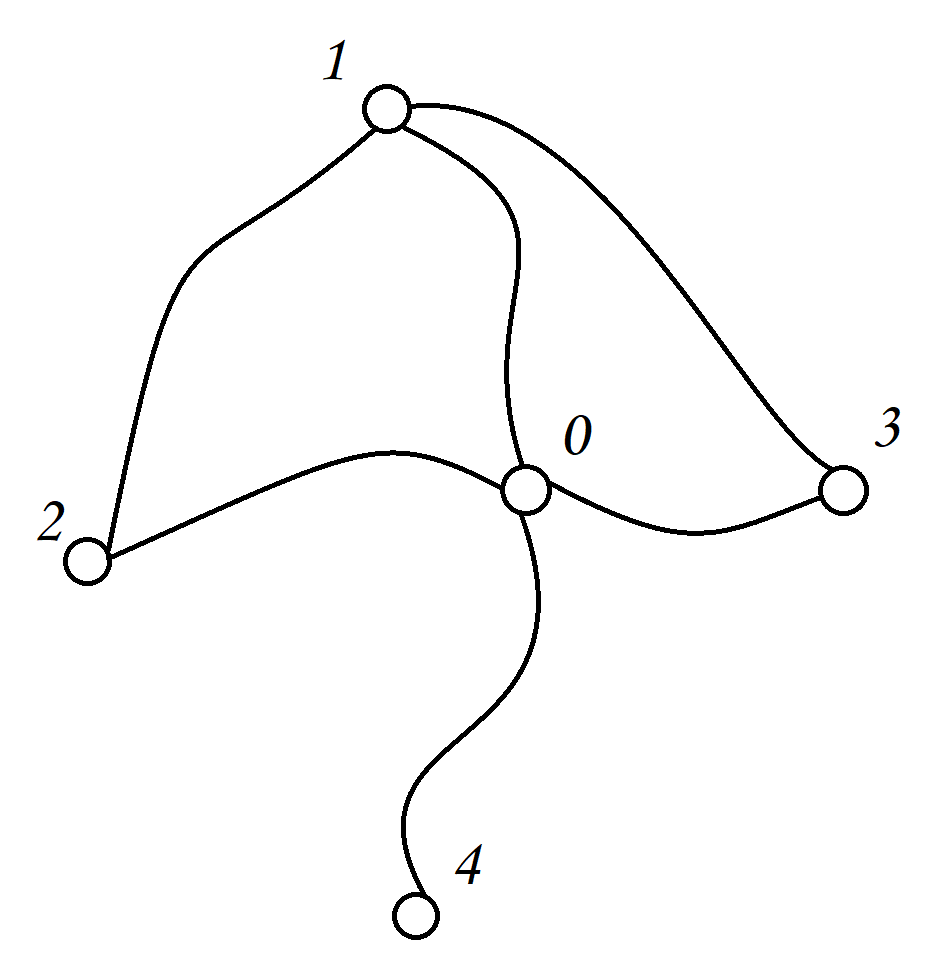
带权图:
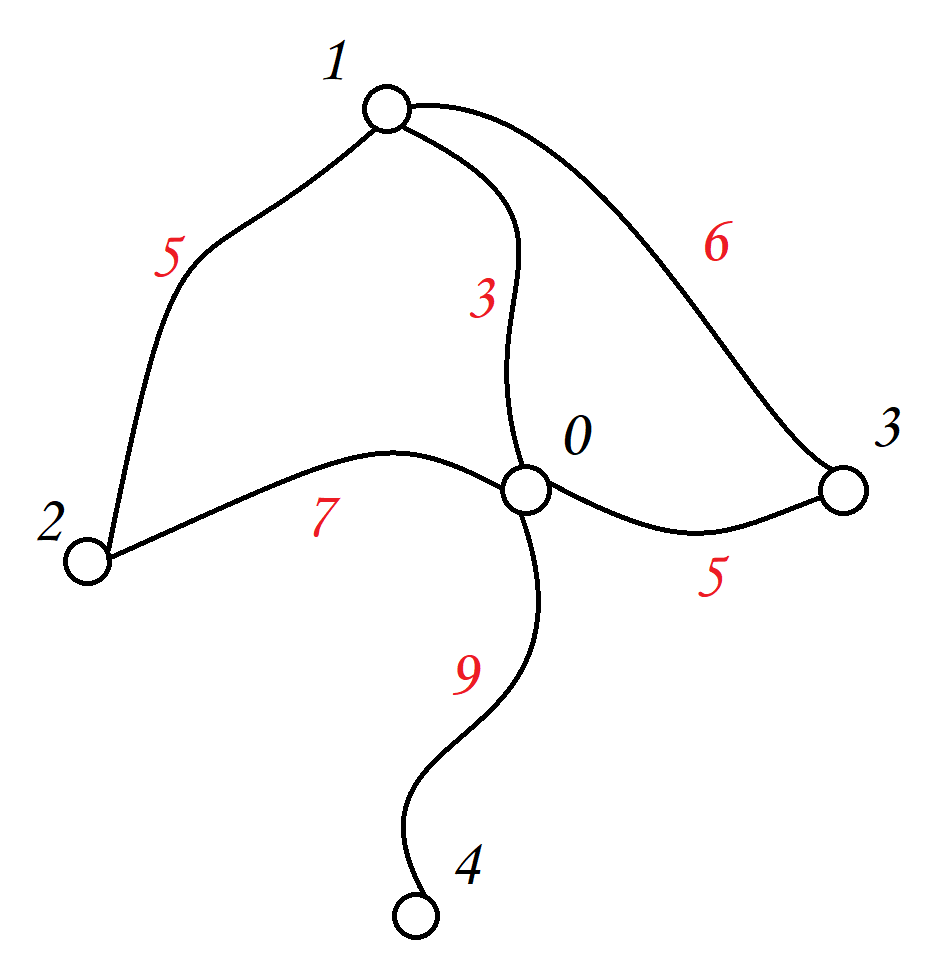
与无权图相对,带权图中的边有各自的权重,这个权重可以表示很多的意义,如距离、时间、成本等等,取决于你要了解的问题,比如,在导航应用中,每个结点可以代表一个结点,边的权重就可以代表两个地点之间的距离或者是行驶时间,在这种情况下,你不仅关心结点之间是否存在边,还关心这个边的权重是多少
2.邻接矩阵的概念
注意:对于邻接矩阵而言 ,不需要去考虑是有向的还是无向的,统一都可以理解成有向的,因为有向图可以兼容无向图,对于无向图而言,只不过这个矩阵按照主对角线对称,因为A到B有变,则必然B到A有边
1.无权图的邻接矩阵
在这样一个矩阵里:
1.矩阵中的行和列都是对应图中的一个顶点
2.如果顶点A到顶点B有一条边(这里是单向的),则对应矩阵单元为1
3.如果顶点A到顶点B没有边,则对应的矩阵单元就为0
如下图所示:
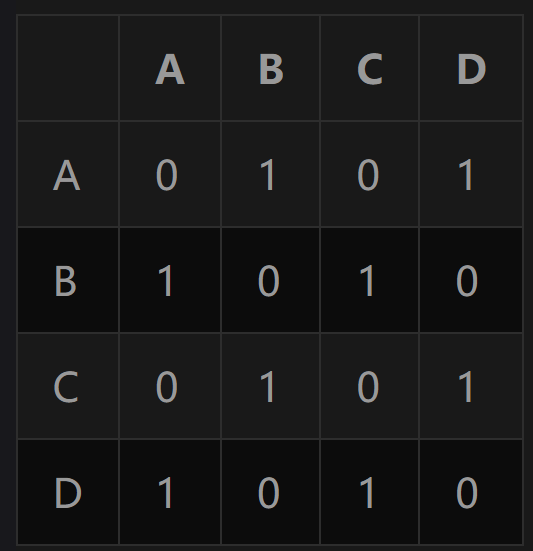
从这个矩阵中我们可以看出,A节点能够到达B、D节点,B节点能够到达A、C节点,C节点能够到达B、D节点,D节点能够到达A、C节点,所以如图所示:
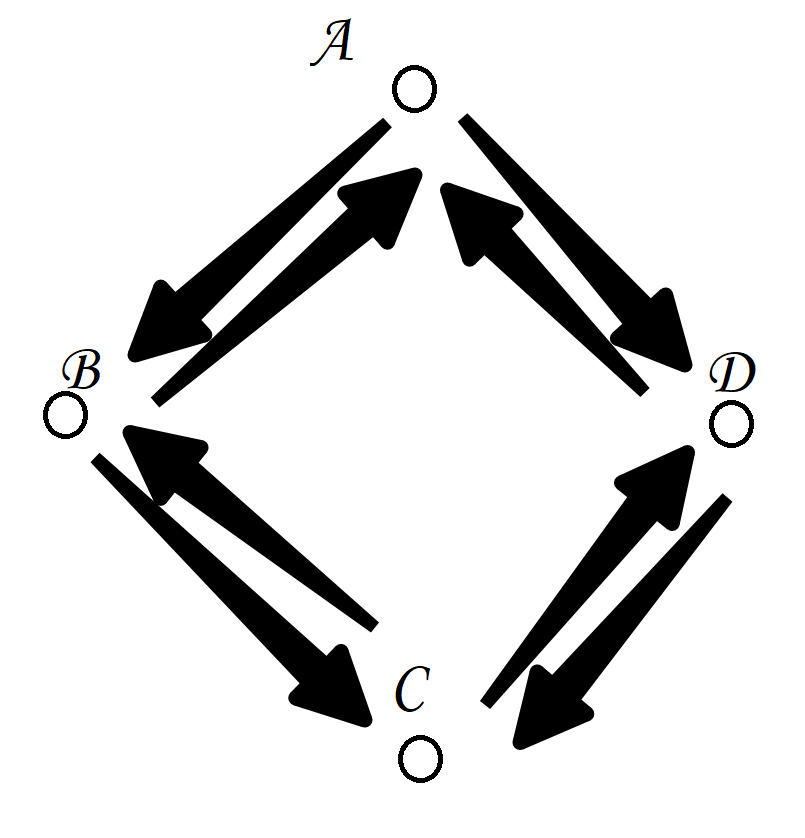
2.带权图的邻接矩阵
在带权图的邻接矩阵中,每个矩阵元素表示一个有向边的权值,如果不存在从一个结点到另一个节点的边,则通常将其表示为特殊的值(0、-1均可)
- A->B 权重为3
- A->C 权重为7
- B->A 权重为4
- B->D 权重为1
- C->D 权重为2
- D->A 权重为1
该邻接矩阵为:

3.邻接矩阵的代码实现
/*** 图的表示--使用邻接矩阵*/
public class Graph01 {private char[] V;//顶点上的值private Vertex[] vertexs;//顶点数组private int N;//邻接矩阵private int[][] adj;//图的构造函数public Graph01(char[] arr) {//{'A','E','F','G','H','P'}//拿到数组的长度int length = arr.length;this.N = length;V = new char[length];//arr元素赋值 到Vthis.V = Arrays.copyOf(arr, length);//构建图中的结点vertexs = new Vertex[length];for (int i = 0; i < length; i++) {vertexs[i] = new Vertex(i,this.V[i]);//}this.adj = new int[length][length];}//打印邻接矩阵public void show() {System.out.print(" ");for (int i = 0; i < this.N; i++) {System.out.format("%4c", this.V[i]);}System.out.println();for (int i = 0; i < this.N; i++) {System.out.format("%4c",this.V[i]);for (int j = 0; j < this.N; j++) {System.out.format("%4s", this.adj[i][j] > 0?(this.adj[i][j]):"-");}System.out.println();}}/*** 创建顶点类*/private class Vertex {char v;//值int index;//索引public Vertex(int index, char c) {this.index = index;this.v = v;}}public static void main(String[] args) {char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};//构建graph01Graph01 graph01 = new Graph01(arr);//进行连接int[][] adjMatrix = graph01.adj;adjMatrix[0][1]=1;adjMatrix[0][2]=1;adjMatrix[0][3]=1;adjMatrix[1][0]=1;adjMatrix[1][3]=1;adjMatrix[1][4]=1;adjMatrix[2][0]=1;adjMatrix[3][0]=1;adjMatrix[3][1]=1;adjMatrix[3][4]=1;adjMatrix[3][5]=1;adjMatrix[4][1]=1;adjMatrix[4][3]=1;adjMatrix[4][5]=1;adjMatrix[5][3]=1;adjMatrix[5][4]=1;graph01.show();}*** 图的表示--使用邻接矩阵*/
public class Graph02 {private char[] V;//顶点上的值private Vertex[] vertexs;//顶点数组private int N;//邻接矩阵private List<Integer>[] adj;//图的构造函数public Graph02(char[] arr) {//{'A','E','F','G','H','P'}//拿到数组的长度int length = arr.length;this.N = length;V = new char[length];//arr元素赋值 到Vthis.V = Arrays.copyOf(arr, length);//构建图中的结点vertexs = new Vertex[length];for (int i = 0; i < length; i++) {vertexs[i] = new Vertex(i, this.V[i]);}this.adj = new List[length];for (int i = 0; i < this.N; i++) {this.adj[i]=new ArrayList<>();}}//打印邻接矩阵public void show() {System.out.println(" ");for (int i = 0; i < this.N; i++) {System.out.format("%-4c", this.V[i]);//拿到邻接表相邻结点的集合List<Integer> linkedList = this.adj[i];for (int j = 0; j < linkedList.size(); j++) {System.out.print(this.V[linkedList.get(j)] + "---->");}System.out.println();System.out.format("%-4d",vertexs[i].index);for (int j = 0; j < linkedList.size(); j++) {System.out.print(vertexs[linkedList.get(j)].index + "---->");}System.out.println();}}/*** 创建顶点类*/private class Vertex {char v;//值int index;//索引int weight;//权值public Vertex(int index, char c) {this.index = index;this.v = v;this.weight = weight;}public Vertex(int index) {}}public static void main(String[] args) {char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};//构建graph01Graph02 graph02 = new Graph02(arr);//邻接表List<Integer>[] adj = graph02.adj;adj[0].add(1);adj[0].add(2);adj[0].add(3);adj[1].add(0);adj[1].add(3);adj[1].add(4);adj[2].add(0);adj[3].add(0);adj[3].add(1);adj[3].add(4);adj[3].add(5);adj[4].add(1);adj[4].add(3);adj[4].add(5);adj[5].add(3);adj[5].add(4);graph02.show();}leetcode题单:
省份数量
//进行广度优先搜索public int findCircleNum(int[][] isConnected) {if(isConnected==null||isConnected.length==0){return 0;}int privice=0;Queue<Integer> queue=new LinkedList<>();boolean[] visited=new boolean[isConnected.length];Arrays.fill(visited,false);//对每一个城市进行遍历,得到每一个城市与相连的城市表for (int i = 0; i <isConnected.length; i++) {//如果是没有遍历过的城市,则进行如下操作if(!visited[i]){queue.offer(i);while(!queue.isEmpty()){int index=queue.poll();visited[index]=true;for (int j = 0; j <isConnected.length; j++) {if(isConnected[index][j]==1&&!visited[j]){queue.offer(j);}}}privice++;} }return privice;}矩阵中的最长递增路径
LCP07.传递信息
相关文章:

一起来学算法(邻接矩阵)
前言: 邻接矩阵是数学和计算机科学中常用的一种表示方式,用来表述有向图或无向图,一张图由一组顶点(或结点)和一组表组成,用邻接矩阵就能表示这些顶点间存在的边的关系 1.图的概念 对于图而言,…...
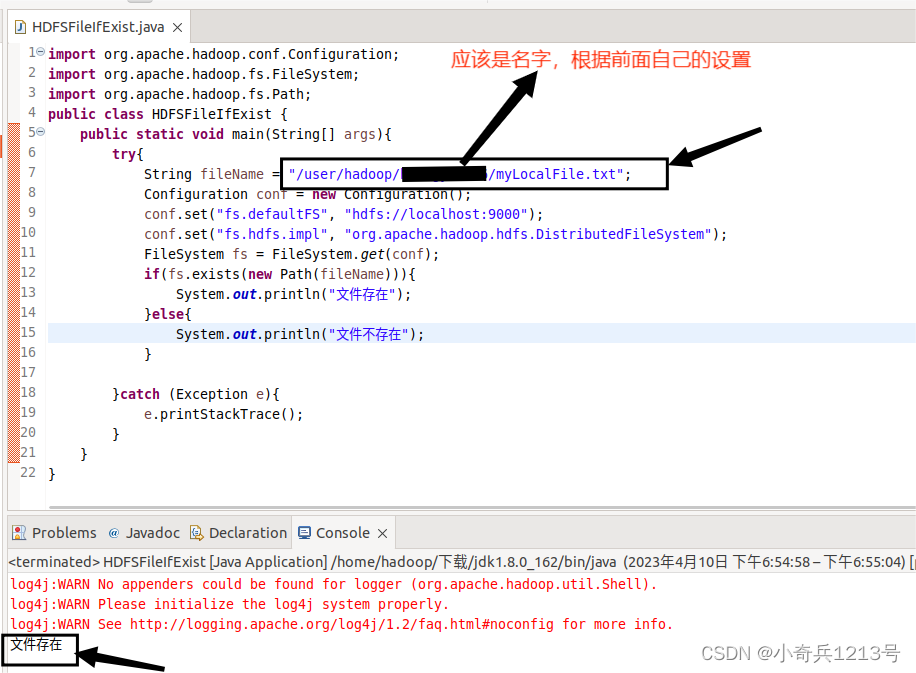
hadoop与HDFS交互
一、利用Shell命令与HDFS进行交互 在进行HDFS编程实践前,需要首先启动Hadoop。可以执行如下命令启动Hadoop: cd /usr/local/hadoop ./sbin/start-dfs.sh #启动hadoop Hadoop支持很多Shell命令,其中fs是HDFS最常用的命令,利用fs…...
)
MYSQL 分区如何指定不同存储路径(多块磁盘)
理论 可以针对分区表的每个分区指定存储路径,对于innodb存储引擎的表只能指定数据路径,因为数据和索引是存储在一个文件当中,对于MYISAM存储引擎可以分别指定数据文件和索引文件,一般也只有RANGE、LIST分区、sub子分区才有可能需要…...
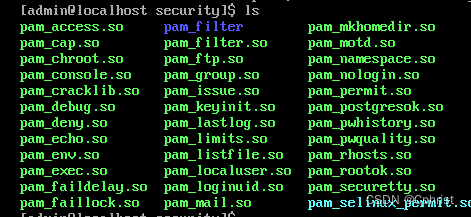
安全加固服务器
根据以下的内容来加固一台Linux服务器的安全。 首先是限制连续密码错误的登录次数,由于RHEL8之后都不再使用pam_tally.so和pam_tally2.so,而是pam_faillock.so 首先进入/usr/lib64/security/中查看有什么模块,确认有pam_faillock.so 因为只…...

Linux 命令学习:
1. PS命令 ps 的aux和-ef区别 1、输出风格不同,展示的格式略有不同 两者的输出结果差别不大,但展示风格不同。aux是BSD风格,-ef是System V风格。 2、aux会截断command列,而-ef不会,当结合grep时这种区别会影响到结果 …...
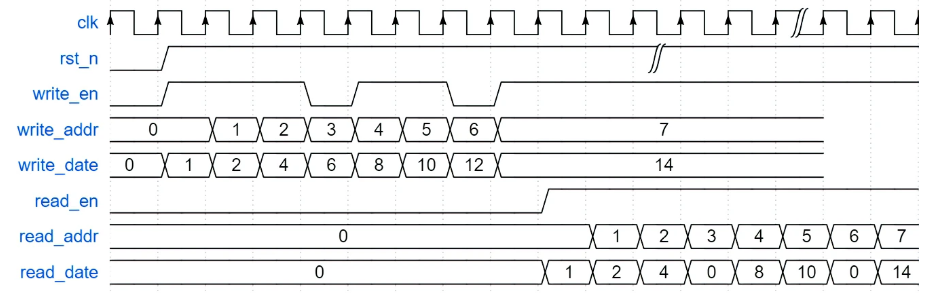
牛客网Verilog刷题——VL54
牛客网Verilog刷题——VL54 题目答案 题目 实现一个深度为8,位宽为4bit的双端口RAM,数据全部初始化为0000。具有两组端口,分别用于读数据和写数据,读写操作可以同时进行。当读数据指示信号read_en有效时,通过读地址信号…...
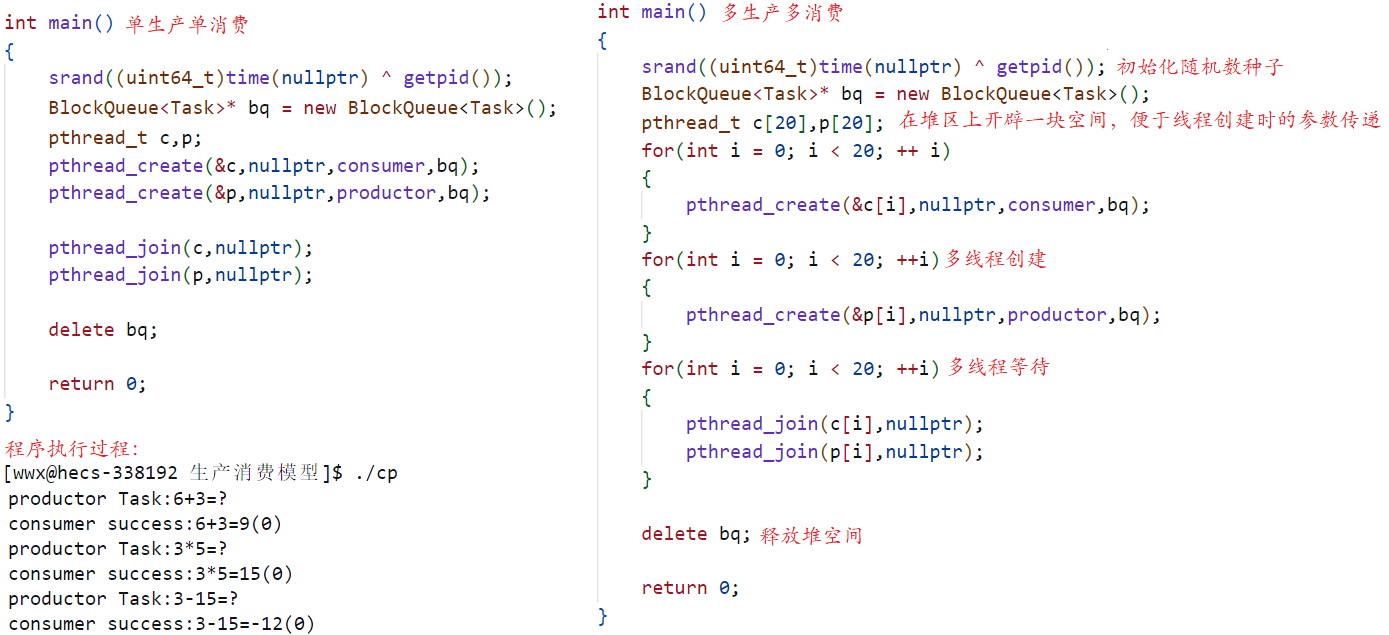
学习系统编程No.34【线程同步之信号量】
引言: 北京时间:2023/7/29/16:34,一切尽在不言中,前几天追了几部电视剧,看了几部电影,刷了n个视屏,在前天我们才终于从这快乐的日子里恢复过来,然后看了两节课,也就是上…...

SolidUI社区-Snakemq 通信源码分析
背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目,旨在将自然语言处理(NLP)与计算机图形学相…...

【大数据之Flume】四、Flume进阶之复制和多路复用、负载均衡和故障转移、聚合案例
1 复制和多路复用 (1)需求:使用 Flume-1 监控文件变动(可以用Exec Source或Taildir Source),Flume-1 将变动内容传递给 Flume-2(用Avro Sink传),(用Avro Sou…...
前端学习--vue2--插槽
写在前面: 这个用法是在使用组件和创建组件中 文章目录 介绍简单使用多个插槽省写默认/后备内容作用域插槽常用实例Element-ui的el-table 废弃用法slot attributeslot-scope attribute 介绍 我们在定义一些组件的时候,由于组件内文字想要自定义&#…...
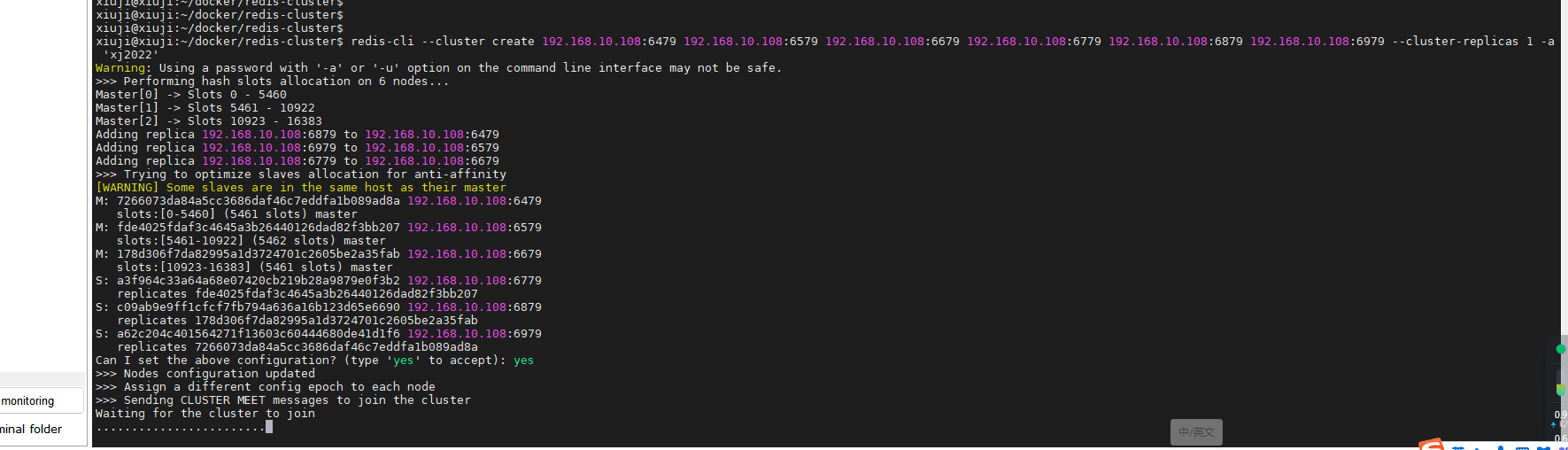
使用 Docker Compose 部署 Redis Cluster 集群,轻松搭建高可用分布式缓存
Redis Cluster(Redis 集群)是 Redis 分布式解决方案的一部分,它旨在提供高可用性、高性能和横向扩展的功能。Redis Cluster 能够将多个 Redis 节点组合成一个分布式集群,实现数据分片和负载均衡,从而确保在大规模应用场…...

在Spring Boot框架中集成 Spring Security
在Spring Boot框架中集成 Spring Security 目录 技术介绍SpringSecurity的核心功能:SpringSecurity特点:具体实现 1、集成依赖2、修改spring security实现service.impl.UserDetailsServiceImpl类 代码1具体解释代码2具体解释 实现config.SecurityConfi…...

登月再进一步:Apollo自动驾驶的里程碑
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★前端炫酷代码分享 ★ ★ uniapp-从构建到提升★ ★ 从0到英雄,vue成神之路★ ★ 解决算法,一个专栏就够了★ ★ 架…...
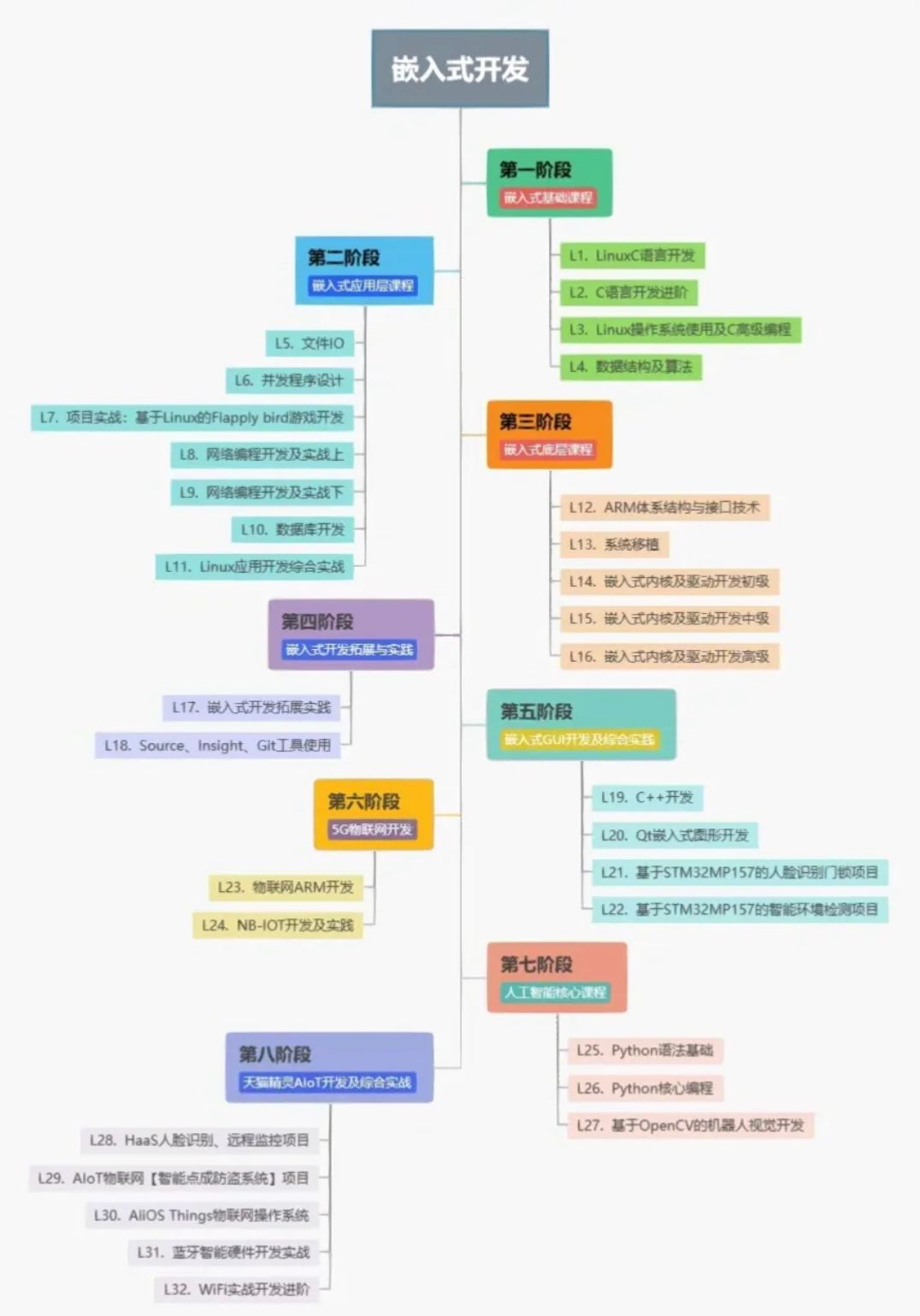
嵌入式一开始该怎么学?学习单片机
学习单片机: 模电数电肯定必须的,玩单片机大概率这两门课都学过,学过微机原理更好。 直接看野火的文档,芯片手册,外设手册。 学单片机不要纠结于某个型号,我认为stm32就OK,主要是原理和感觉。…...

Spring事件监听器ApplicationListener
目录 介绍 spirng启动后启动某方法 介绍 ApplicationEvent以及Listener是Spring为我们提供的一个事件监听、订阅的实现,内部实现原理是观察者设计模式,设计初衷也是为了系统业务逻辑之间的解耦,提高可扩展性以及可维护性。事件发布者并不需…...
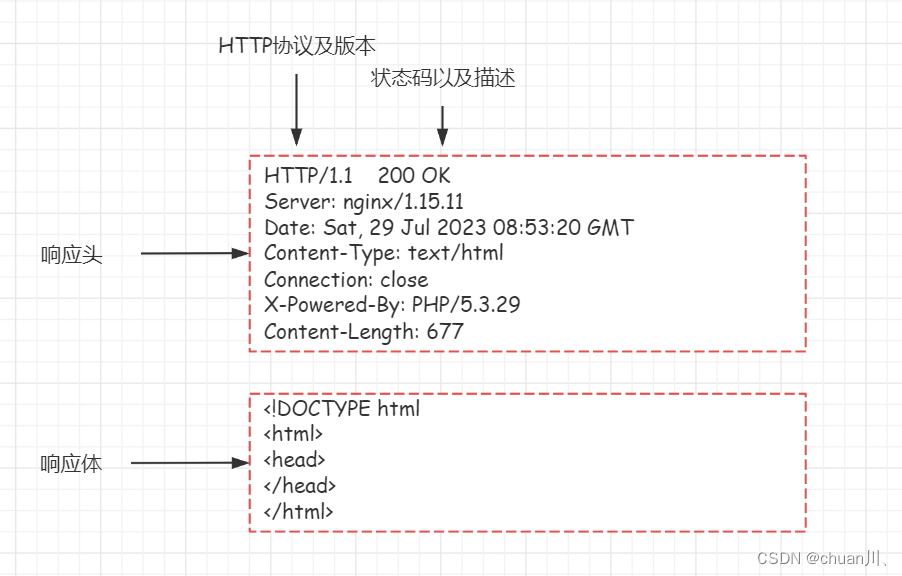
安全学习DAY10_HTTP数据包
HTTP数据包 文章目录 HTTP数据包小节导图Request请求数据包结构Request请求方法(方式)请求头(Header)Response响应数据包结构Response响应数据包状态码状态码作用:部分状态码详解判断网站文件是否存在的状态码…...

云原生落地实践的25个步骤
一、什么是云原生? 云原生从字面意思上来看可以分成云和原生两个部分。 云是和本地相对的,传统的应用必须跑在本地服务器上,现在流行的应用都跑在云端,云包含了IaaS,、PaaS和SaaS。 原生就是土生土长的意思,我们在开始…...

Stable diffusion 三大基础脚本 提示词矩阵,载入提示词,XYZ图表讲解
目录 0.本章讲解 1.提示词矩阵(prompt matrix) 1.2.提示词矩阵功能选项 1.2.1.把可变部分放在提示词文本的开头 1.2.2.为每张图片使用不同随机种子 1.2.3.选择提示词 1.2.4.选择分割符 1.2.5.宫格图边框(像素) 2.从文本框或文件载入提示词(Pro…...
uniapp uni-combox 下拉提示无匹配项(完美解决--附加源码解决方案及思路)
问题描述 匆匆忙忙又到了周一啦,一大早就来了一个头疼的问题,把我难得团团转,呜呜呜~ 下面我用代码的方式展示出来,看下你的代码是否与我的不同。 解决方案 <uni-forms-item label"名称" name"drugName&quo…...

10. Mybatis 项目的创建
目录 1. Mybatis 概念 2. 第一个 Mybits 查询 2.1 创建数据库和表 2.2 添加 Mybatis 框架支持 2.3 添加配置文件 2.4 配置 MyBatis 中的 XML 路径 2.5 添加业务代码 在学习 Mybatis 之前,我们需要知道 Mybatis 和 Spring 没有任何的关系。如果一定要强调二者…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
