生成模型相关算法:EM算法步骤和公式推导
EM算法
- 引言
- EM算法例子及解法
- EM算法步骤和说明
引言
EM 算法是一种选代算法,1977 年 Dempster 等人总结提出,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计EM算法的每次选代由两步组成:E步,求期望 (expectation);M步,求极大(maximization)所以这一算法称为期望极大算法(expectation maximizationalgorithm),简称EM算法。
EM算法例子及解法
三硬币模型: 假设有3 硬币,分别作 A , B , C A,B,C A,B,C这些硬币正面出现的概率分别是 π \pi π, p p p和 q q q进行如下硬币试验:先硬币 A A A,根据其结果选出硬币 B B B或硬币 C C C,正面选硬币 B B B,反面选硬币 C C C;然后掷选出的硬币,掷硬币的结果,出现正面记作 1,出现反面记作 0;独立地重复$n $次试验(这里,n=10),观测结果如下:
1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 1,1,0,1,0,0,1,0,1,1 1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数。
模型表达是为:
P ( y ∣ θ ) = ∑ z P ( y , z ∣ θ ) = ∑ z P ( z ∣ θ ) P ( y ∣ z , θ ) = π p y ( 1 − p ) y + ( 1 − π ) q y ( 1 − q ) 1 − y \begin{align} P(y|\theta) &= \sum_{z}P(y,z|\theta)=\sum_{z}P(z|\theta)P(y|z,\theta) \nonumber\\ &=\pi p^y (1-p)^y+(1-\pi)q^y(1-q)^{1-y} \nonumber \end{align} P(y∣θ)=z∑P(y,z∣θ)=z∑P(z∣θ)P(y∣z,θ)=πpy(1−p)y+(1−π)qy(1−q)1−y
这里,随机变量 y y y是观测变量,表示一次试验观测的结果是 1或0;随机变量是隐变量,表示未观测到的掷硬币 A A A 的结果; θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)是模型参这一模型是以上数据的生成模型,注意,随机变量 y y y的数据可以观测,随机变量 z z z的数据不可观测。
将观察数据表示为 Y = ( Y 1 , Y 1 , . . . , Y 1 ) T Y=(Y_1,Y_1,...,Y_1)^T Y=(Y1,Y1,...,Y1)T,未观察数据表示为 Z = ( Z 1 , Z 2 , . . . , Z n ) T Z=(Z_1,Z_2,...,Z_n)^T Z=(Z1,Z2,...,Zn)T,则观察数据的似然函数为
P ( Y ∣ θ ) = ∑ z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) P(Y|\theta)=\sum_zP(Z|\theta)P(Y|Z,\theta) P(Y∣θ)=z∑P(Z∣θ)P(Y∣Z,θ)
即
P ( Y ∣ θ ) = ∏ j = 1 n [ π p y j ( 1 − p ) y j + ( 1 − π ) q y j ( 1 − q ) 1 − y j ] P(Y|\theta)=\prod_{j=1}^{n}[\pi p^{y_j} (1-p)^{y_j}+(1-\pi)q^{y_j}(1-q)^{1-{y_j}}] P(Y∣θ)=j=1∏n[πpyj(1−p)yj+(1−π)qyj(1−q)1−yj]
考虑求模型参数 θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)的极大似然估计,即
θ ^ = a r g max θ l o g P ( Y ∣ θ ) \hat{\theta}=arg \max\limits_{\theta}logP(Y|\theta) θ^=argθmaxlogP(Y∣θ)
这个问题没有解析解,只有通过迭代的方法求解。EM算法就是可以用于求解这个问题的一种迭代算法下面给出针对以上问题的EM算法其推导过程省略。
EM算法首先选取参数的初值,记作 θ ( 0 ) = ( π ( 0 ) , p ( 0 ) , q ( 0 ) ) \theta^{(0)}=(\pi^{(0)},p^{(0)},q^{(0)}) θ(0)=(π(0),p(0),q(0)),然后通过下面的迭代参数的估计值,直至收敛为止。第 i i i次迭代参数的估计值为 θ ( 0 ) = ( π ( i ) , p ( i ) , q ( i ) ) \theta^{(0)}=(\pi^{(i)},p^{(i)},q^{(i)}) θ(0)=(π(i),p(i),q(i))。EM 算法的第 i + 1 i+1 i+1次迭代如下。
E步:计算在模型参数 π ( i ) , p ( i ) , q ( i ) \pi^{(i)},p^{(i)},q^{(i)} π(i),p(i),q(i)下观测数据 y i y_i yi来自掷硬币B的概率
μ i + 1 = π ( p ( i ) ) y j ( 1 − ( p ( i ) ) ) y j π ( p ( i ) ) y j ( 1 − ( p ( i ) ) ) y j + ( 1 − π ) ( q ( i ) ) y j ( 1 − ( q ( i ) ) ) 1 − y j \mu^{i+1}=\frac{\pi (p^{(i)})^{y_j} (1- (p^{(i)}))^{y_j}}{\pi (p^{(i)})^{y_j} (1- (p^{(i)}))^{y_j}+(1-\pi)(q^{(i)})^{y_j}(1-(q^{(i)}))^{1-{y_j}}} μi+1=π(p(i))yj(1−(p(i)))yj+(1−π)(q(i))yj(1−(q(i)))1−yjπ(p(i))yj(1−(p(i)))yj
M步:计算模型参数的新估计值
π ( i + 1 ) = 1 n ∑ j = 1 n μ j ( i + 1 ) \pi^{(i+1)}=\frac{1}{n} \sum_{j=1}^{n} \mu_j^{(i+1)} π(i+1)=n1j=1∑nμj(i+1)
p ( i + 1 ) = ∑ j = 1 n μ j ( i + 1 ) y j ∑ j = 1 n μ j ( i + 1 ) p^{(i+1)}=\frac{ \sum_{j=1}^{n} \mu_j^{(i+1)}y_j}{ \sum_{j=1}^{n} \mu_j^{(i+1)}} p(i+1)=∑j=1nμj(i+1)∑j=1nμj(i+1)yj
q ( i + 1 ) = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) y j ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) q^{(i+1)}=\frac{ \sum_{j=1}^{n} (1-\mu_j^{(i+1)})y_j}{ \sum_{j=1}^{n} (1-\mu_j^{(i+1)})} q(i+1)=∑j=1n(1−μj(i+1))∑j=1n(1−μj(i+1))yj
进行数字计算,假设模型参数的初值为
π ( 0 ) = 0.5 , p ( 0 ) = 0.5 , q ( 0 ) = 0.5 \pi^{(0)}=0.5,p^{(0)}=0.5,q^{(0)}=0.5 π(0)=0.5,p(0)=0.5,q(0)=0.5
对 y j = 1 y_j=1 yj=1与 y j = 0 y_j=0 yj=0均有 μ j ( 1 ) = 0.5 \mu_j^{(1)}=0.5 μj(1)=0.5。
根据M步计算得到
π ( 0 ) = 0.5 , p ( 0 ) = 0.6 , q ( 0 ) = 0.6 \pi^{(0)}=0.5,p^{(0)}=0.6,q^{(0)}=0.6 π(0)=0.5,p(0)=0.6,q(0)=0.6
根据E步,可以得到
μ j ( 2 ) = 0.5 , j = 1 , 2 , . . . , 10 \mu_j^{(2)}=0.5,j=1,2,...,10 μj(2)=0.5,j=1,2,...,10
继续迭代,得
π ( 0 ) = 0.5 , p ( 0 ) = 0.6 , q ( 0 ) = 0.6 \pi^{(0)}=0.5,p^{(0)}=0.6,q^{(0)}=0.6 π(0)=0.5,p(0)=0.6,q(0)=0.6
于是得到模型参数 θ \theta θ的极大似然估计:
π ^ = 0.5 , p ^ = 0.6 , q ^ = 0.6 \hat{\pi}=0.5,\hat p=0.6,\hat q=0.6 π^=0.5,p^=0.6,q^=0.6
π = 0.5 \pi=0.5 π=0.5表示硬币A是匀称的,这一结果容易理解。
如果取初始值 π ( 0 ) = 0.4 , p ( 0 ) = 0.6 , q ( 0 ) = 0.7 \pi^{(0)}=0.4,p^{(0)}=0.6,q^{(0)}=0.7 π(0)=0.4,p(0)=0.6,q(0)=0.7,那么得到的模型参数的极大似然估计 π ^ = 0.4064 , p ^ = 0.5368 , q ^ = 0.6432 \hat{\pi}=0.4064,\hat p=0.5368,\hat q=0.6432 π^=0.4064,p^=0.5368,q^=0.6432。这就是说,EM算法与初始值的选择有关,选择不同的初值可能得到不同的参数估计值。
EM算法步骤和说明
一般地,用Y表示观测随机变量的数据,Z表示隐随机变量的数据Y和Z连在一起称为完全数据 (complete-data),观测数据Y又称为不完全数据(incomplete-data)。假设给定观测数据Y,其概率分布是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),其中是需要估计的模型参数,那么不完全数据Y的似然函数是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),对数似然函数 L ( 0 ) = l o g P ( Y ∣ θ ) L(0)=logP(Y|\theta) L(0)=logP(Y∣θ);假设Y和Z的联合概率分布是 P ( Y Z ∣ θ ) P(YZ|\theta) P(YZ∣θ),那完全的对数似然函数是 l o g P ( Y , Z ∣ θ ) logP(Y,Z|\theta) logP(Y,Z∣θ)。
EM算法通过选代求 L ( θ ) = l o g P ( Y ∣ θ ) L(\theta)=logP(Y|\theta) L(θ)=logP(Y∣θ)的极大似然估计每次代包含两步:E 步,求期望:M步,求极大化,下面来介绍 EM 算法。
输入:观测变量数据 Y Y Y,隐变量数据 Z Z Z,联合分布 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ),条件分布 P ( Z ∣ Y , θ ) P(Z|Y,\theta) P(Z∣Y,θ);
输出:模型参数 θ \theta θ。
(1)选择参数的初值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)E步:记 θ ( i ) \theta^{(i)} θ(i)为第 i i i次代参数的估计值,在第 i + 1 i+1 i+1次选代的E步,计算
Q ( θ , θ ( i ) ) = E Z [ l o g P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z l o g P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) \begin{align} Q(\theta,\theta^{(i)}) &=E_Z[logP(Y,Z|\theta)|Y,\theta^{(i)}] \nonumber\\ &=\sum_{Z}logP(Y,Z|\theta)P(Z|Y,\theta^{(i)}) \nonumber\\ \end{align} Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)]=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
这里, P ( Z ∣ Y , θ ) P(Z|Y,\theta) P(Z∣Y,θ)在给定观测数据 Y Y Y和当前的参数估计 θ ( i ) \theta^{(i)} θ(i)下隐变量数据 Z Z Z的条件概率分布;
(3)M步:求使 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))极大化的 θ \theta θ,确定第 i + 1 i+1 i+1次迭代的参数的估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)
θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)}=\arg \max \limits_{\theta}Q(\theta,\theta^{(i)}) θ(i+1)=argθmaxQ(θ,θ(i))
(4)重复第(2)步和第(3)步,直到收敛。
函数 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))是EM算法的核心,称为Q函数(Q function)。
下面关于 EM 算法作几点说明:
步骤(1)参数的初值可以任意选择,但需注意 EM算法对初值是敏感的步骤(2)E步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))。Q函数式中Z是未观察数据,Y是观测数据注意, Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))的第1个变元表示要极大化的参数,第2个变元表示参数的当前估计值。每次迭代实际在求 Q Q Q函数及其极大。
步骤(3)M步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))的极大化,得到 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),完成一次代 θ ( i ) − > θ ( i + 1 ) \theta^{(i)}->\theta^{(i+1)} θ(i)−>θ(i+1)。后面将证明每次迭代使似然函数增大或达到局部极值。
步骤(4)给出停止迭代的条件,一般是对较小的正数 ϵ 1 , ϵ 2 \epsilon_1,\epsilon_2 ϵ1,ϵ2,若满足
∣ ∣ θ ( i + 1 ) − θ ( i ) ∣ ∣ < ϵ 1 或 ∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ < ϵ 2 || \theta^{(i+1)}- \theta^{(i)}||<\epsilon_1 或||Q(\theta^{(i+1)},\theta^{(i)})- Q(\theta^{(i)},\theta^{(i)})||<\epsilon_2 ∣∣θ(i+1)−θ(i)∣∣<ϵ1或∣∣Q(θ(i+1),θ(i))−Q(θ(i),θ(i))∣∣<ϵ2
则停止迭代
相关文章:

生成模型相关算法:EM算法步骤和公式推导
EM算法 引言EM算法例子及解法EM算法步骤和说明 引言 EM 算法是一种选代算法,1977 年 Dempster 等人总结提出,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计EM算法的每次选代由两步组成:E步,求…...

Compose手势
Compose手势 本文链接: 点击 拖动 滑动 锚点 Compose Drag 拖动原理 Compose Drag 拖动原理:等待第一次按下 挂起 // UI展现出来的时候,这个while循环就已经在等待第一次按下了。事件 -> 恢复判断拖动合法性合法onDragStartonDragonDragEndforEa…...

【雕爷学编程】Arduino动手做(177)---ESP-32 掌控板2
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...

Ubuntu-文件和目录相关命令
🔮linux的文件系统结构 ⛳目录结构及目录路径 🧩文件系统层次结构标准FHS Filesystem Hierarchy Standard(文件系统层次结构标准) Linux是开源的软件,各Linux发行机构都可以按照自己的需求对文件系统进行裁剪,所以众多…...
)
显式接口实现(C# 编程指南)
接口的实现可以有多种方式,下面是C#接口实现的几种方式欢迎交流 两个接口包含签名相同的成员 如果一个类实现的两个接口包含签名相同的成员,则在该类上实现此成员会导致这两个接口将此成员用作其实现。 如下示例中,所有对 Paint 的调用皆调用同一方法。 第一个示例定义类型…...
)
element-ui 图片上传 及 quillEditor富文本(图片视频上传)
<template><div class"card" style"overflow: hidden; padding-bottom: 10px"><div style"padding: 20px 20px 0 20px"><span class"title_top"><span class"top_icon"></span>基本信息…...
前端技术Vue学习笔记--002
前端技术Vue学习笔记 文章目录 前端技术Vue学习笔记1、指令修饰符2、v-bind对于样式控制的增强2.1、v-bind对于样式控制的增强--class2.2、v-bind对于样式控制的增强--操作style 3、v-model应用于其他表单元素4、计算属性4.1、**computed计算属性 vs methods方法的区别**4.2、计…...
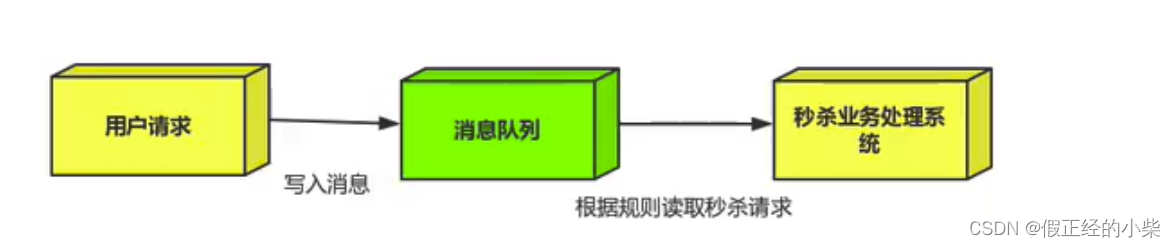
【RabbitMQ(day4)】SpringBoot整合RabbitMQ与MQ应用场景说明
一、SpringBoot 中使用 RabbitMQ 导入对应的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency>配置配置文件 spring:application:name: rabbitmq-springbo…...
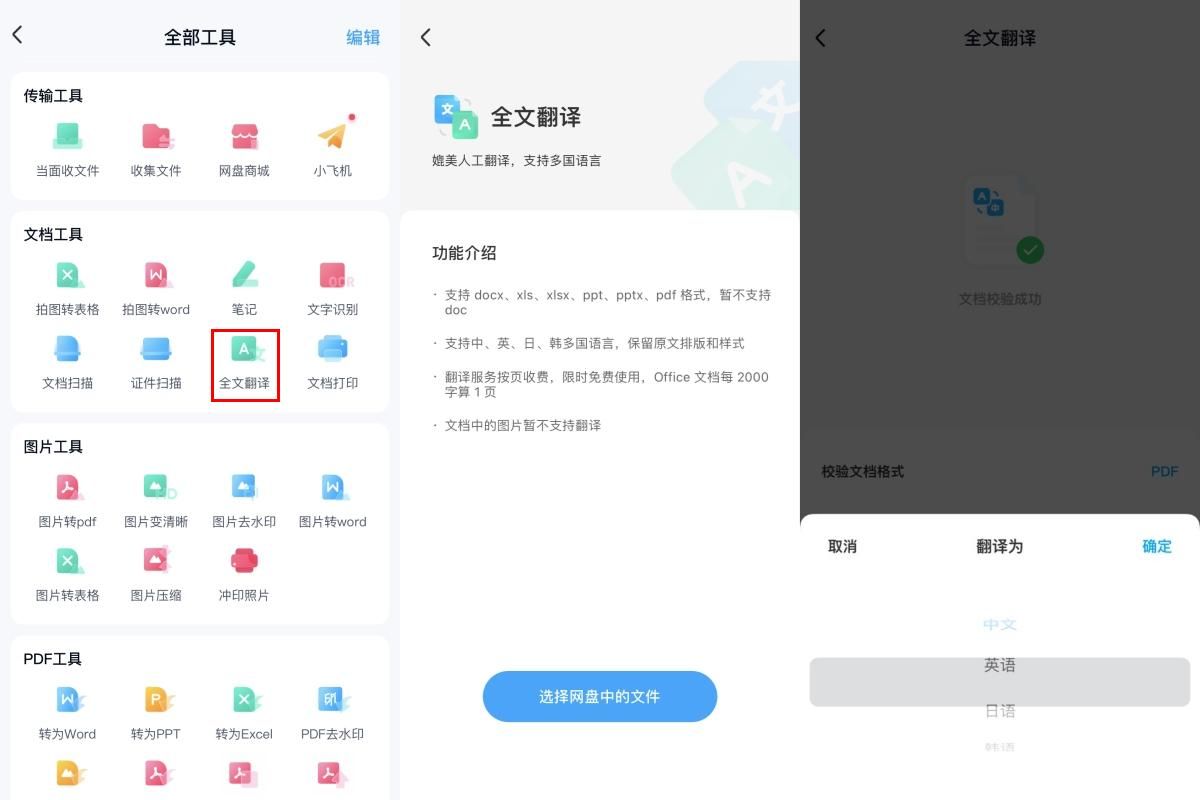
想了解好用的翻译pdf的软件吗?
在全球化的时代背景下,跨国贸易越来越普遍,跨语言沟通也越来越频繁。小黄是一家跨国公司的员工,他梦想能在全球各地拓展自己的业务,奈何遇到了一个巨大的挑战:跨语言沟通。在这其中,pdf文件是他经常接收到的…...
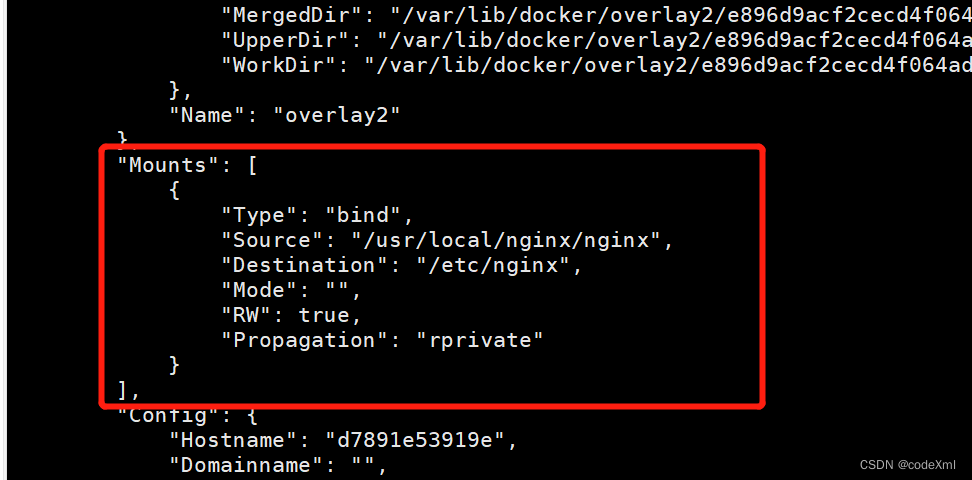
docker安装nginx并配置SSL
1、拉取镜像 docker pull nginx2、启动nginx容器,复制一份默认配置文件出来 // 以nginx镜像为基础镜像创建一个名为nginx01的容器 docker run -d -p 80:80 --name nginx01 nginx创建成功后会看到nginx的欢迎页面 3、挂载nginx目录 拷贝nginx的配置信息到主机目录…...

【LeetCode 算法】Reorder List 重排链表
文章目录 Reorder List 重排链表问题描述:分析代码PointerReverseMerge Tag Reorder List 重排链表 问题描述: 给定一个单链表 L 的头节点 head ,单链表 L 表示为: L0 → L1 → … → Ln - 1 → Ln 请将其重新排列后变为&#…...

MQ面试题3
1、讲一讲Kafka与RocketMQ中存储设计的异同? Kafka 中文件的布局是以 Topic/partition ,每一个分区一个物理文件夹,在分区文件级别实现文件顺序写,如果一个Kafka集群中拥有成百上千个主题,每一个主题拥有上百个分区&am…...

【Linux命令200例】patch 用于将补丁文件应用到源码中
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆本文已收录于专栏:Linux命令大全。 🏆本专栏我们会通过具体的系统的命令讲解加上鲜…...

一起来学算法(邻接矩阵)
前言: 邻接矩阵是数学和计算机科学中常用的一种表示方式,用来表述有向图或无向图,一张图由一组顶点(或结点)和一组表组成,用邻接矩阵就能表示这些顶点间存在的边的关系 1.图的概念 对于图而言,…...
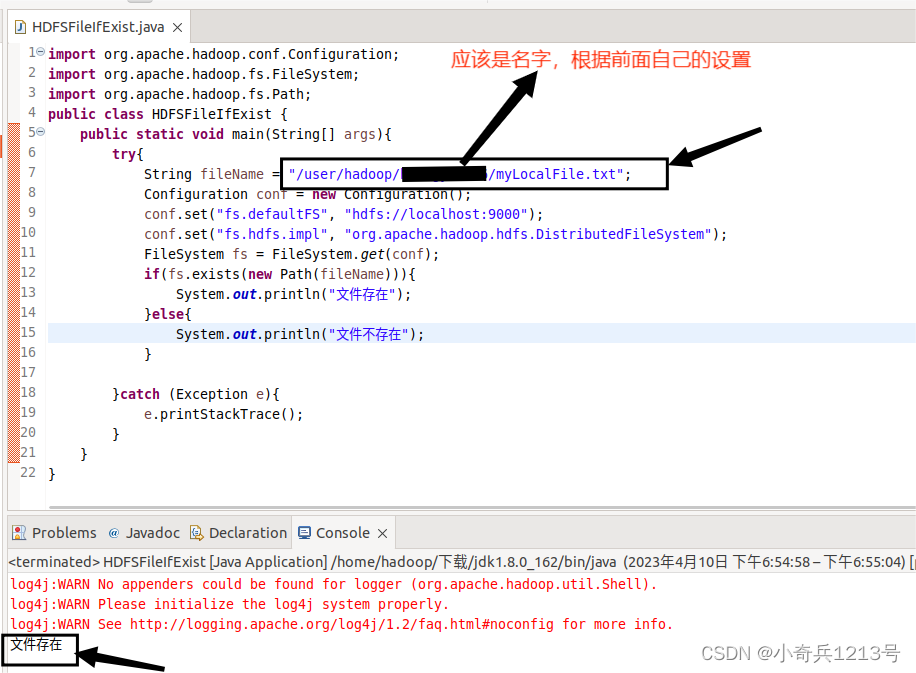
hadoop与HDFS交互
一、利用Shell命令与HDFS进行交互 在进行HDFS编程实践前,需要首先启动Hadoop。可以执行如下命令启动Hadoop: cd /usr/local/hadoop ./sbin/start-dfs.sh #启动hadoop Hadoop支持很多Shell命令,其中fs是HDFS最常用的命令,利用fs…...
)
MYSQL 分区如何指定不同存储路径(多块磁盘)
理论 可以针对分区表的每个分区指定存储路径,对于innodb存储引擎的表只能指定数据路径,因为数据和索引是存储在一个文件当中,对于MYISAM存储引擎可以分别指定数据文件和索引文件,一般也只有RANGE、LIST分区、sub子分区才有可能需要…...
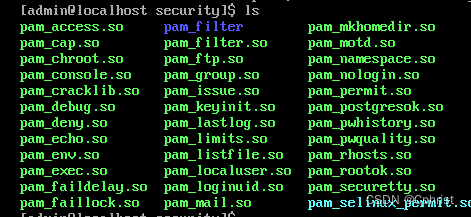
安全加固服务器
根据以下的内容来加固一台Linux服务器的安全。 首先是限制连续密码错误的登录次数,由于RHEL8之后都不再使用pam_tally.so和pam_tally2.so,而是pam_faillock.so 首先进入/usr/lib64/security/中查看有什么模块,确认有pam_faillock.so 因为只…...

Linux 命令学习:
1. PS命令 ps 的aux和-ef区别 1、输出风格不同,展示的格式略有不同 两者的输出结果差别不大,但展示风格不同。aux是BSD风格,-ef是System V风格。 2、aux会截断command列,而-ef不会,当结合grep时这种区别会影响到结果 …...
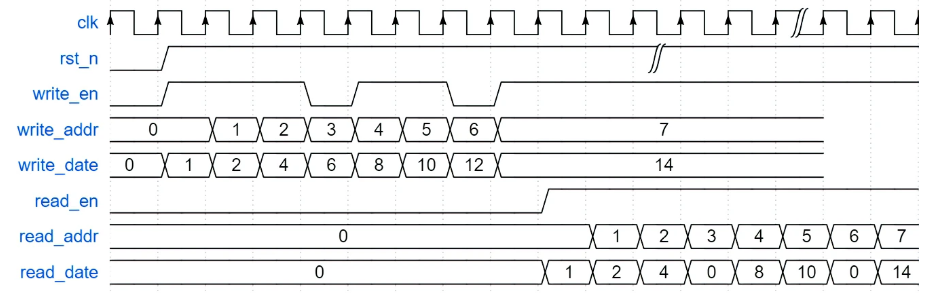
牛客网Verilog刷题——VL54
牛客网Verilog刷题——VL54 题目答案 题目 实现一个深度为8,位宽为4bit的双端口RAM,数据全部初始化为0000。具有两组端口,分别用于读数据和写数据,读写操作可以同时进行。当读数据指示信号read_en有效时,通过读地址信号…...
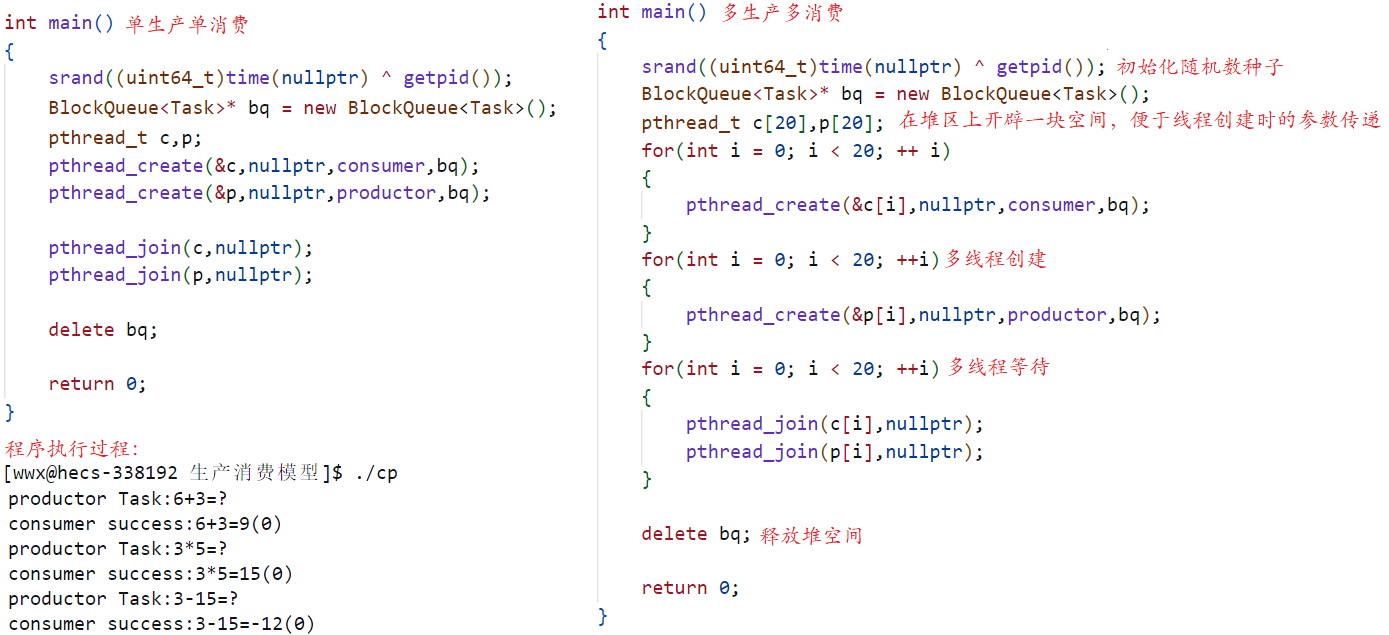
学习系统编程No.34【线程同步之信号量】
引言: 北京时间:2023/7/29/16:34,一切尽在不言中,前几天追了几部电视剧,看了几部电影,刷了n个视屏,在前天我们才终于从这快乐的日子里恢复过来,然后看了两节课,也就是上…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
