数论分块学习笔记
准备开始复习莫比乌斯反演,杜教筛这一部分,先复习一下数论分块
0.随便说说
数论分块可以计算如下形式的式子 ∑ i = 1 n f ( i ) g ( ⌊ n i ⌋ ) \sum_{i=1}^{n}f(i)g(\lfloor\frac{n}{i}\rfloor) ∑i=1nf(i)g(⌊in⌋)。
利用的原理是 ⌊ n i ⌋ \lfloor\frac{n}{i}\rfloor ⌊in⌋的不同的值不超过 2 n 2\sqrt{n} 2n个。
当我们可以在 O ( 1 ) O(1) O(1)的时间快速处理出 ∑ i = l r f ( i ) \sum_{i=l}^{r}f(i) ∑i=lrf(i)或提前预处理出 f ( x ) f(x) f(x)的前缀和时,上述式子可在 O ( n ) O(\sqrt{n}) O(n)的时间计算出来。
1.代码实现
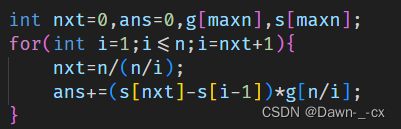
怎么找每个块是个问题,有个结论:
设块的左端点为 ⌊ n l ⌋ \lfloor\frac{n}{l}\rfloor ⌊ln⌋,右端点为 ⌊ n r ⌋ \lfloor\frac{n}{r}\rfloor ⌊rn⌋,则 r = ⌊ n ⌊ n l ⌋ ⌋ r=\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor r=⌊⌊ln⌋n⌋。
证明也挺好证的 设 k = ⌊ n i ⌋ , k=\lfloor\frac{n}{i}\rfloor, k=⌊in⌋,则 k ≤ n i , k\le \frac{n}{i}, k≤in,
因此 ⌊ n k ⌋ ≥ ⌊ n n i ⌋ = i \lfloor\frac{n}{k}\rfloor\ge\lfloor\frac{n}{\frac{n}{i}}\rfloor=i ⌊kn⌋≥⌊inn⌋=i,即 i ≤ ⌊ n k ⌋ = ⌊ n ⌊ n i ⌋ ⌋ i\le\lfloor\frac{n}{k}\rfloor=\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor i≤⌊kn⌋=⌊⌊in⌋n⌋因此右端点 r = i m a x = ⌊ n ⌊ n i ⌋ ⌋ r=i_{max}=\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor r=imax=⌊⌊in⌋n⌋。
因此每个块为 i = l i=l i=l到 i = ⌊ n ⌊ n i ⌋ ⌋ i=\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor i=⌊⌊in⌋n⌋。
2.例题
先顺手把 O I W i k i OI\,\,Wiki OIWiki上的三个例题做了吧
UVA11526 H(n)
题面
用洛谷的题面了,这题就是求 ∑ i = 1 n ⌊ n i ⌋ \sum_{i=1}^{n}\lfloor\frac{n}{i}\rfloor ∑i=1n⌊in⌋,就是板子题,相当于 f ( x ) = 1 , g ( n / i ) = n / i f(x)=1,g(n/i)=n/i f(x)=1,g(n/i)=n/i。注意如果 n = 2147483647 n=2147483647 n=2147483647,最后一次 n x t + 1 nxt+1 nxt+1会爆 i n t int int, U V A UVA UVA神奇 o j oj oj会报 R E RE RE,所以就都开 l o n g l o n g long\,\,long longlong就行,时间复杂度 O ( T n ) O(T\sqrt{n}) O(Tn)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t,n;
int main(){cin>>t;while(t--){cin>>n;ll nxt=0,ans=0;for(ll i=1;i<=n;i=nxt+1){nxt=n/(n/i);ans+=(nxt-i+1)*(n/i);}cout<<ans<<endl;}
}P2261 [CQOI2007] 余数求和
题面
Solution
O I OI OI时期的博客有这道题,题解挂链接了,随手一推就是这样,减号左边是 n k , nk, nk,右侧用数论分块做
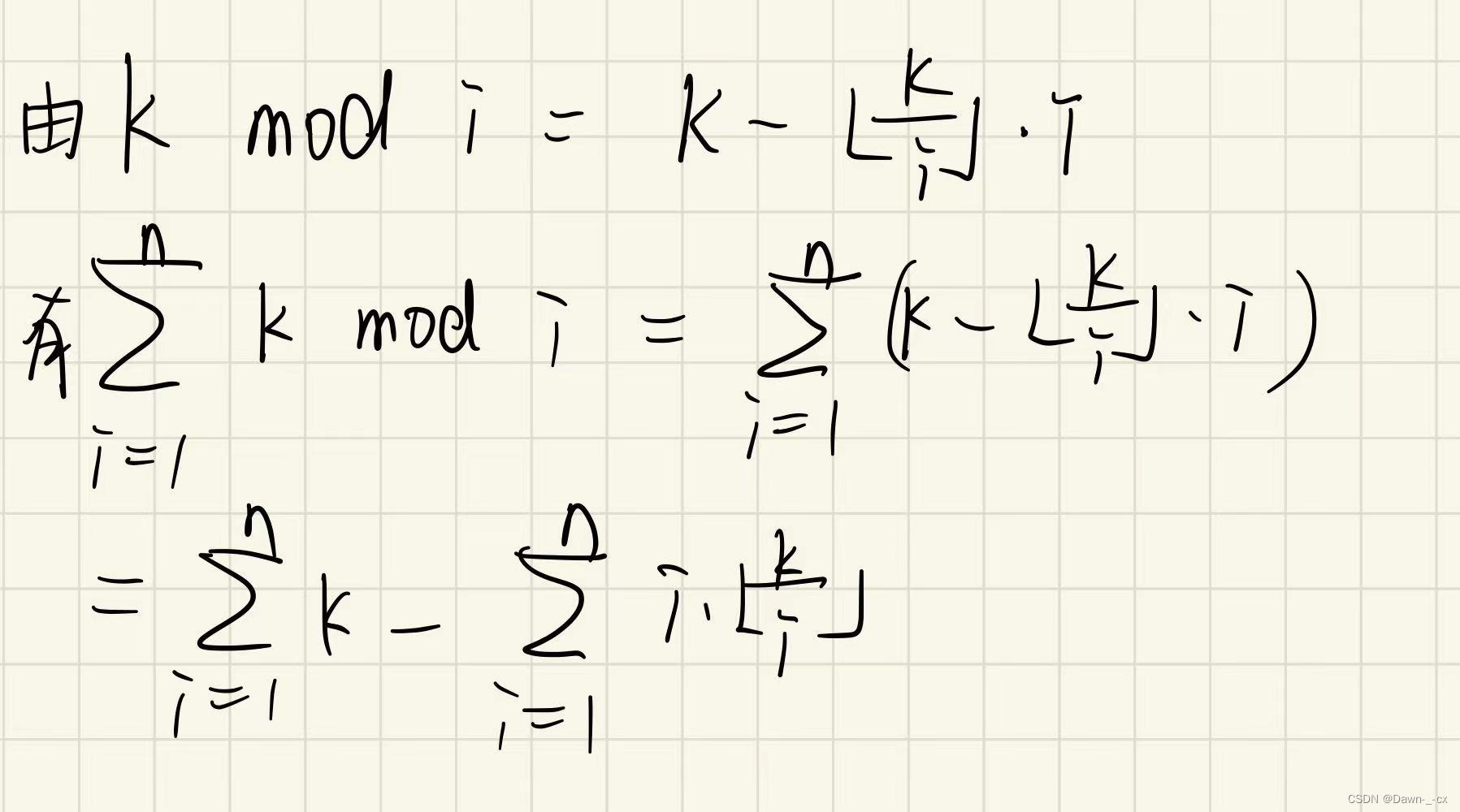
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k,ans,nxt,sum;
inline ll s(ll n){return n*(n+1)/2;
}
int main(){cin>>n>>k;ans=n*k;for(int i=1;i<=min(n,k);i=nxt+1){nxt=min(k/(k/i),n);sum+=(s(nxt)-s(i-1))*(k/i);}cout<<ans-sum<<endl;
}
P3455 [POI2007] ZAP-Queries
题面

最后用个二维数论分块就可
闲得没事 这题想多打几个空格
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e4 + 100;
int cnt, pri[maxn], mu[maxn], s_mu[maxn];
bool vis[maxn];
inline void read(int &x) {int s = 0, w = 1; char ch = getchar();while (ch < '0' || ch > '9') {if(ch == '-') w = -1; ch = getchar(); }while (ch >= '0' && ch <= '9') {s = (s << 3) + (s << 1) + (ch & 15); ch = getchar(); }x = s * w;
}
void setup() {mu[1] = 1;for (int i = 2; i <= maxn - 100; i++) {if(!vis[i]) pri[++cnt] = i, mu[i] = -1;for (int j = 1; j <=cnt && i * pri[j] <= maxn - 100; j++) {vis[i * pri[j]] = true;if(i % pri[j]) mu[i * pri[j]] = -mu[i];else {mu[i * pri[j]] = 0;break;}}}for (int i = 1; i <= maxn - 100; i++) s_mu[i] = s_mu[i - 1] + mu[i];
}
int T, a, b, d, nxt;
int main() {setup();read(T);while(T--) {read(a), read(b), read(d);a /= d, b /= d;if(a > b) a ^= b, b ^= a, a ^= b;ll ans = 0;for (int i = 1; i <= a; i = nxt + 1) {nxt = min(a / (a / i), b / (b / i));ans += 1ll * (s_mu[nxt] - s_mu[i - 1]) * (a / i) * (b / i);}printf("%lld\n", ans);}
}
放两道套路题,这一类题都是以 ∑ i = 1 n ∑ j = 1 n f ( g c d ( i , j ) ) \sum_{i=1}^{n}\sum_{j=1}^{n}f(gcd(i,j)) ∑i=1n∑j=1nf(gcd(i,j))形式的,我们要将 g c d ( i , j ) gcd(i,j) gcd(i,j)提出来,作如下变化:
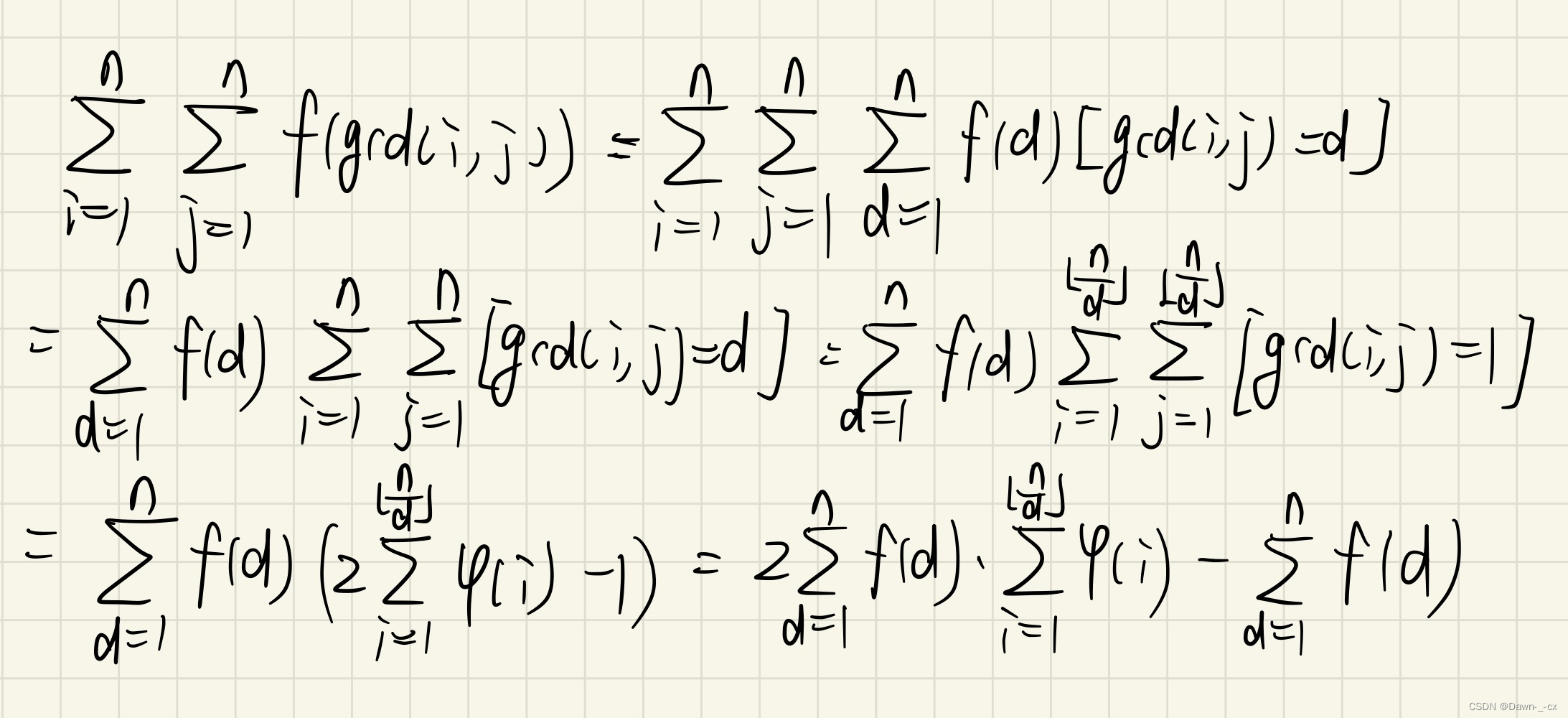
然后求出 f ( x ) , ϕ ( x ) f(x),\phi(x) f(x),ϕ(x)的前缀和并应用数论分块解决。
后面两题的数据范围不一样,第一题是 n ≤ 1 e 7 n\le 1e7 n≤1e7,第二题是 n ≤ 1 e 9 n\le 1e9 n≤1e9,前者可以应用朴素的筛法求出欧拉函数前缀和,后者要用到杜教筛进行求解。
bzoj4804 欧拉心算
题面
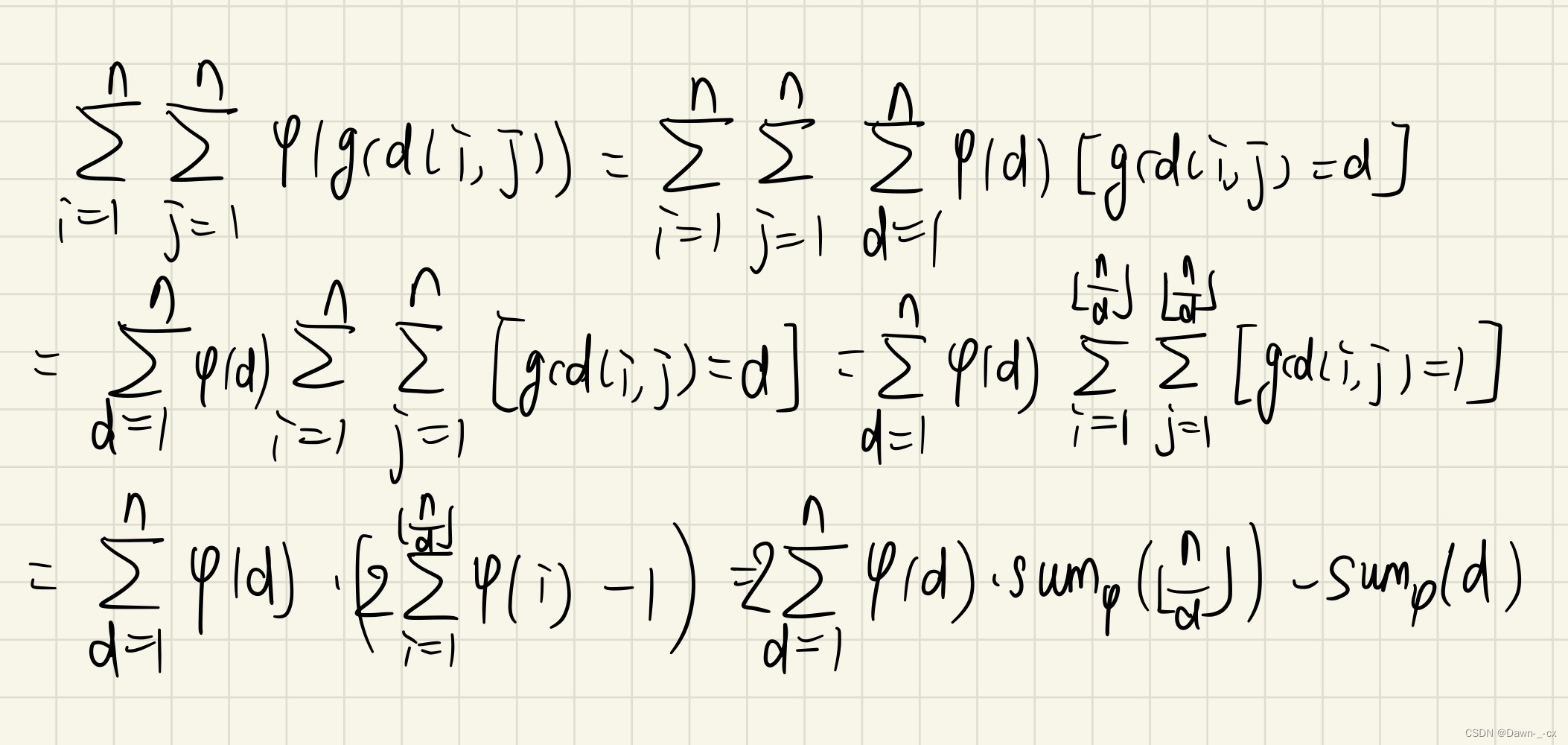
预处理出欧拉函数前缀和,应用数论分块即可。
写错了,最后是 s u m ϕ ( n ) sum\phi(n) sumϕ(n)。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 1e7 + 10;
int cnt, pri[maxn], euc[maxn];
ll s[maxn];
bool vis[maxn];
void setup(){euc[1] = 1;for (int i = 2; i <= maxn - 10; i++) {if (!vis[i]) pri[++cnt] = i, euc[i] = i - 1;for (int j = 1; j <= cnt && i * pri[j] <= maxn - 10; j++) {vis[i * pri[j]] = true;if (i % pri[j]) euc[i * pri[j]] = euc[i] * (pri[j] - 1);else {euc[i * pri[j]] = pri[j] * euc[i];break;}}}for (int i = 1; i <= maxn - 10; i++) s[i] = s[i - 1] + euc[i];
}
int T, n;
int main() {setup();scanf("%d", &T);while (T--) {scanf("%d", &n);int nxt = 0; ll ans = 0;for (int i = 1; i <= n; i = nxt + 1) {nxt = n / (n / i);ans += (s[nxt] - s[i - 1]) * s[n / i];}printf("%lld\n", 2ll * ans - s[n]);}
}HDU7325 GCD Magic
题面
考场上考到得,打了 150 150 150行, M L E MLE MLE了一次, W A WA WA了一次,最后过了
M L E MLE MLE是因为对 s b H D U O J sbHDUOJ sbHDUOJ不信任,预处理的 1 e 7 1e7 1e7的欧拉函数前缀和,后来改成了 2 e 6 2e6 2e6, W A WA WA了,看了一会儿发现是因为杜教筛欧拉函数前缀和没模 m o d mod mod导致后面计算答案时候爆 l o n g l o n g long\,\,long longlong了,改过来交一发对了,太不容易了,这要再错真不知道要 d e b u g debug debug到哪年去。
思路如下,就不打公式了,太多了,手写了。
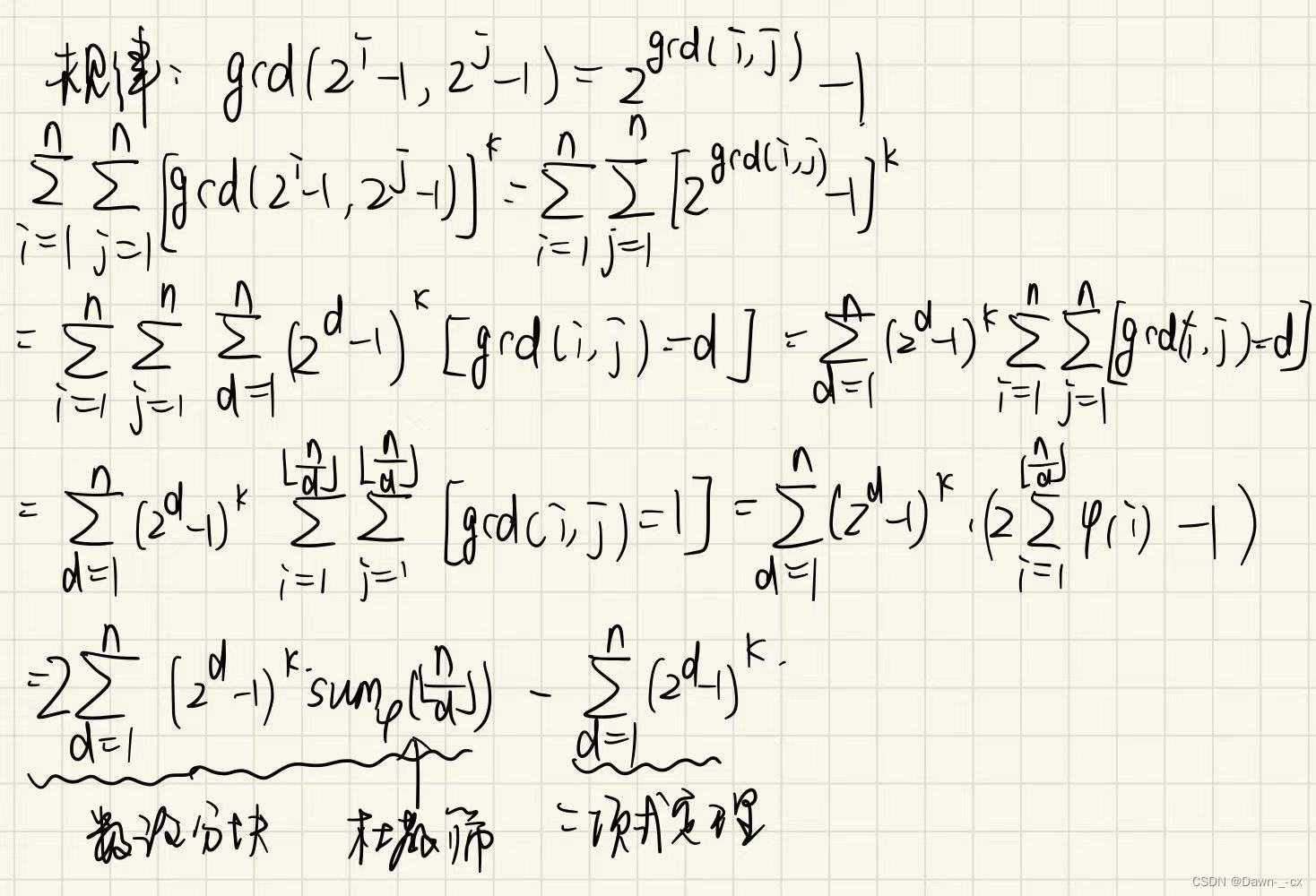
上代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int maxn = 2000010;
inline void read(int &x)
{int s = 0, w = 1;char ch = getchar();while (ch < '0' || ch > '9'){if (ch == '-')w = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch & 15);ch = getchar();}x = s * w;
}
ll ans, s[maxn], frac[20], fracinv[20];
int t, n, k, lst;
ll pri[maxn], euc[maxn], cur, mu[maxn], sum_mu[maxn];
bool vis[maxn];
map<ll, ll> mp_mu;ll S_mu(ll x)
{if (x < maxn)return sum_mu[x];if (mp_mu[x])return mp_mu[x];ll ret = (ll)1;for (ll i = 2, j; i <= x; i = j + 1){j = x / (x / i);ret -= S_mu(x / i) * (j - i + 1);}return mp_mu[x] = ret % mod;
}ll S_phi(ll x)
{ll ret = (ll)0;ll j;for (ll i = 1; i <= x; i = j + 1){j = x / (x / i);ret += (S_mu(j) - S_mu(i - 1)) * (x / i) * (x / i);}return ((ret - 1) / 2 + 1) % mod;
}
inline ll qpow(ll x, ll y)
{ll re = 1LL;while (y){if (y & 1)(re *= x) %= mod;(x *= x) %= mod;y >>= 1;}return re;
}
inline ll inv(ll x)
{return qpow(x, mod - 2);
}
void setup()
{frac[0] = fracinv[0] = 1LL;for (int i = 1; i <= 15; i++)frac[i] = 1ll * frac[i - 1] * i % mod;fracinv[15] = inv(frac[15]);for (int i = 14; i; i--)fracinv[i] = 1ll * fracinv[i + 1] * (i + 1) % mod;euc[1] = 1;mu[1] = 1;for (int i = 2; i < maxn; i++){if (!vis[i]){pri[++cur] = i;mu[i] = -1;euc[i] = i - 1;}for (int j = 1; j <= cur && i * pri[j] < maxn; j++){vis[i * pri[j]] = true;if (i % pri[j])mu[i * pri[j]] = -mu[i], euc[i * pri[j]] = euc[i] * euc[pri[j]];else{mu[i * pri[j]] = 0;euc[i * pri[j]] = euc[i] * pri[j];break;}}}for (int i = 1; i < maxn; i++)s[i] = (1ll * s[i - 1] + euc[i]) % mod;for (int i = 1; i < maxn; i++)sum_mu[i] = (1ll * sum_mu[i - 1] + mu[i]) % mod;
}
inline ll C(ll n, ll m)
{if (n < m)return 0;return 1ll * frac[n] * fracinv[m] % mod * fracinv[n - m] % mod;
}
inline ll seq(ll n, ll k)
{if (k == 0)return n;ll a1 = (1LL << k) % mod, q = (1LL << k) % mod;return 1LL * a1 * ((qpow(q, n) - 1 + mod) % mod) % mod * inv((q - 1 + mod) % mod) % mod;
}
inline ll sg(ll n, ll k)
{if (n == 0)return 0LL;ll ans = 0, flag = 1;for (int i = 0; i <= k; i++){ans = (1ll * ans + 1ll * ((flag + mod) % mod) * C(k, i) % mod * seq(n, k - i) % mod) % mod;flag *= (-1ll);}return ans % mod;
}
int main()
{setup();read(t);while (t--){read(n), read(k);ans = 0ll;lst = 0;for (int i = 1; i <= n; i = lst + 1){lst = n / (n / i);ll snow = 0;if (n / i >= maxn - 10)snow = S_phi(n / i);elsesnow = s[n / i];ans = (1ll * ans + (1ll * sg(lst, k) - sg(i - 1, k) + mod) % mod * snow % mod) % mod;}printf("%lld\n", (2LL * ans % mod - sg(n, k) + mod) % mod);}
}
相关文章:
数论分块学习笔记
准备开始复习莫比乌斯反演,杜教筛这一部分,先复习一下数论分块 0.随便说说 数论分块可以计算如下形式的式子 ∑ i 1 n f ( i ) g ( ⌊ n i ⌋ ) \sum_{i1}^{n}f(i)g(\lfloor\frac{n}{i}\rfloor) ∑i1nf(i)g(⌊in⌋)。 利用的原理是 ⌊ n i ⌋ \lf…...
【基础理论】了解点过程
Maximum tsunami wave height generated by the 16 Sept. 2015 Chile earthquake, from the International Tsunami Information Center. Posted by Austin Elliott 一、说明 在这个世界上,会发生许多事件,其趋势可能遵循一种模式。在这篇博客中&#…...

深入理解Spring MVC中的@ResponseBody注解
引言 在现代的Web应用开发中,数据的传递和交互是不可或缺的一部分。Spring MVC作为一个强大的框架,在处理客户端请求和响应时,提供了许多注解来简化开发过程。其中,ResponseBody注解在处理方法的返回值时起到了关键作用࿰…...
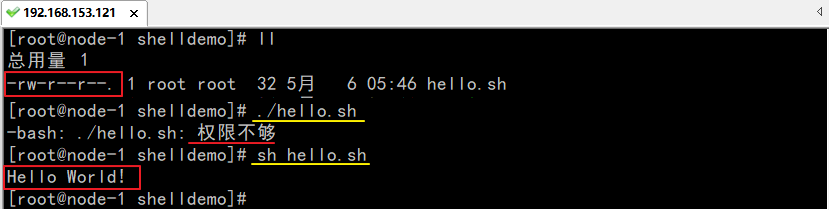
大数据学习教程:Linux高级教程(下)
四、大数据集群服务器搭建 1. 新增Linux服务器 1.1、克隆虚拟机 学习环境中,一般使用VMware虚拟机克隆Linux系统,用来进行集群服务器的搭建。 VMware支持两种类型的克隆:完整克隆、链接克隆 完整克隆是和原始虚拟机完全独立的一个复制&…...

1.Oracle建表及使用
1.概述 1. 表:用于 存储数据 -- 是我们最常见的数据库对象 2. 表设计注意事项 (1) 表设计时,尽量遵从 第三范式(3NF) (2) 名称不能超过 30 个字符 -- 超过会报错 (3) 名称只能以 字母 大头,可由数字、 _、 $…...
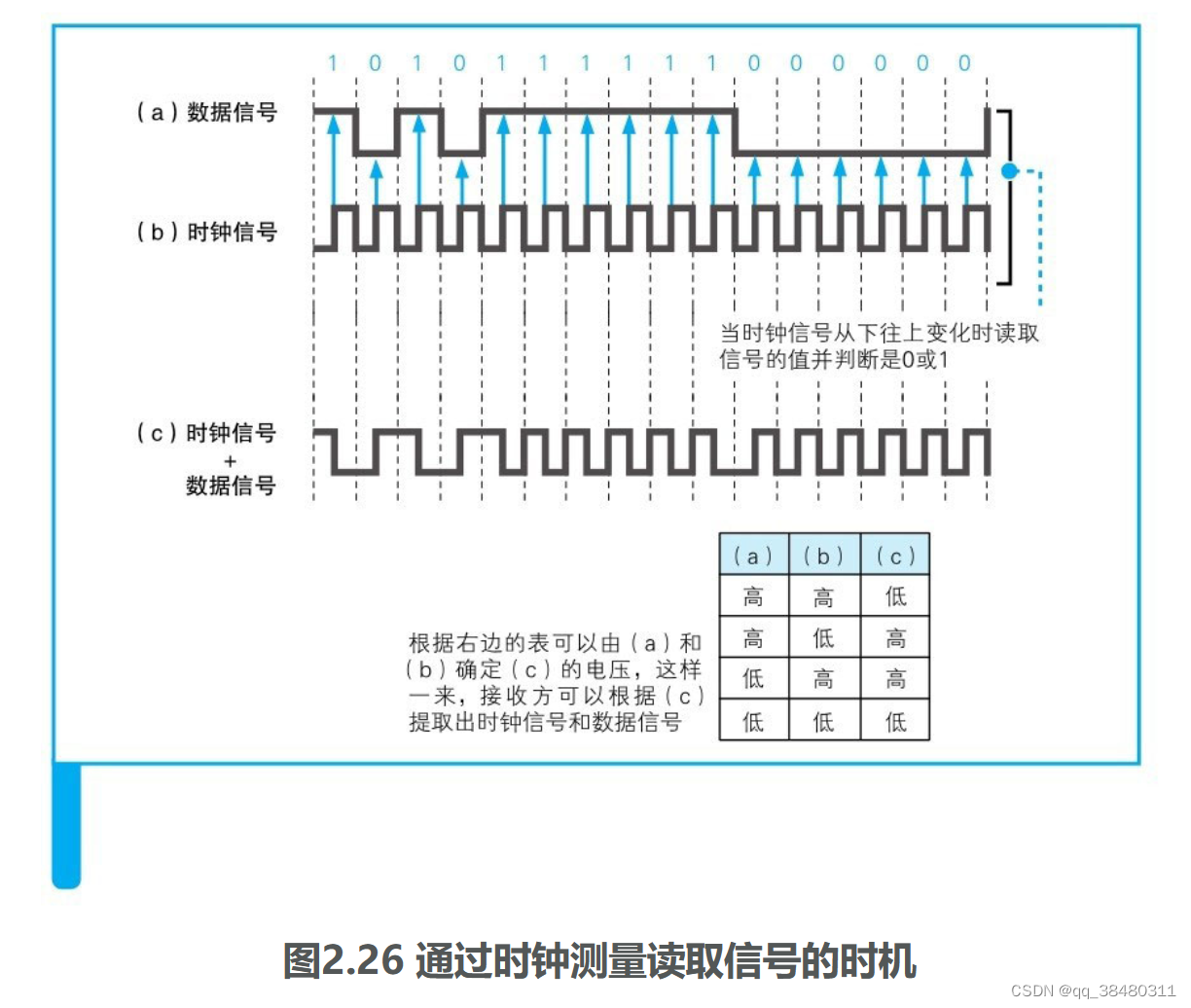
《网络是怎样连接的》(二.2)
(6条消息) 《网络是怎样连接的》(二.1)_qq_38480311的博客-CSDN博客 本文主要取材于 《网络是怎样连接的》 第二章 2.5 2.6章节。 目录 简述: 本文的主要内容是 以太网的收发操作 和 UDP协议的收发操作。 IP与以太网的包收发操作 包是什…...

MySQL加密插件安装
加密插件 查看已经安装的插件:show plugs; 增加加密插件: 登陆MySQL后,通过show variables like ‘validate%’;查看相关验证规则。 ① 在配置文件中新增,[mysqld]标签下 plugin-load-addvalidate_password.so ② 在运行时新增…...

新手入门Jenkins自动化部署入门详细教程
1. 背景 在实际开发中,我们经常要一边开发一边测试,当然这里说的测试并不是程序员对自己代码的单元测试,而是同组程序员将代码提交后,由测试人员测试; 或者前后端分离后,经常会修改接口,然后重新…...
Neural Network学习笔记4
完整的模型训练套路 train.py import torch import torchvision from torch.utils.data import DataLoader # 引入自定义的网络模型 from torch.utils.tensorboard import SummaryWriterfrom model import *# 准备数据集 train_data torchvision.datasets.CIFAR10(root"…...

[转]关于cmake --build .的理解
https://blog.csdn.net/qq_38563206/article/details/126486183 https://blog.csdn.net/HandsomeHong/article/details/120170219 cmake --build . 该命令的含义是:执行当前目录下的构建系统,生成构建目标。 cmake项目构建过程简述: 1. 首先…...
【Linux下6818开发板(ARM)】硬件空间挂载
(꒪ꇴ꒪ ),hello我是祐言博客主页:C语言基础,Linux基础,软件配置领域博主🌍快上🚘,一起学习!送给读者的一句鸡汤🤔:集中起来的意志可以击穿顽石!作者水平很有限,如果发现错误&#x…...

剑指offer 动态规划篇
题目由入门往上递增 入门 斐波那契数列_牛客题霸_牛客网 (nowcoder.com) 动态规划甚至于算法的入门题目 方法一:按照斐波那契的公式fnfn-1fn-2,从1-n求出结果。 class Solution { public:int Fibonacci(int n) {vector<int>f{0,1,1};for(int …...
自动化部署的一些笔记)
关于Linux中前端负载均衡之VIP(LVS+Keepalived)自动化部署的一些笔记
写在前面 整理一些 LVS 相关的笔记理解不足小伙伴帮忙指正 傍晚时分,你坐在屋檐下,看着天慢慢地黑下去,心里寂寞而凄凉,感到自己的生命被剥夺了。当时我是个年轻人,但我害怕这样生活下去,衰老下去。在我看来…...

C++ 拷贝交换技术示例
拷贝交换技术(copy and swap)是什么,网上估计能查到很多。但网上有点难找到完整的演示代码,所以这里记录一下。难点在于: 如果要满足 5 的原则,我到底要写那些函数? 默认构造函数、复制构造函数…...
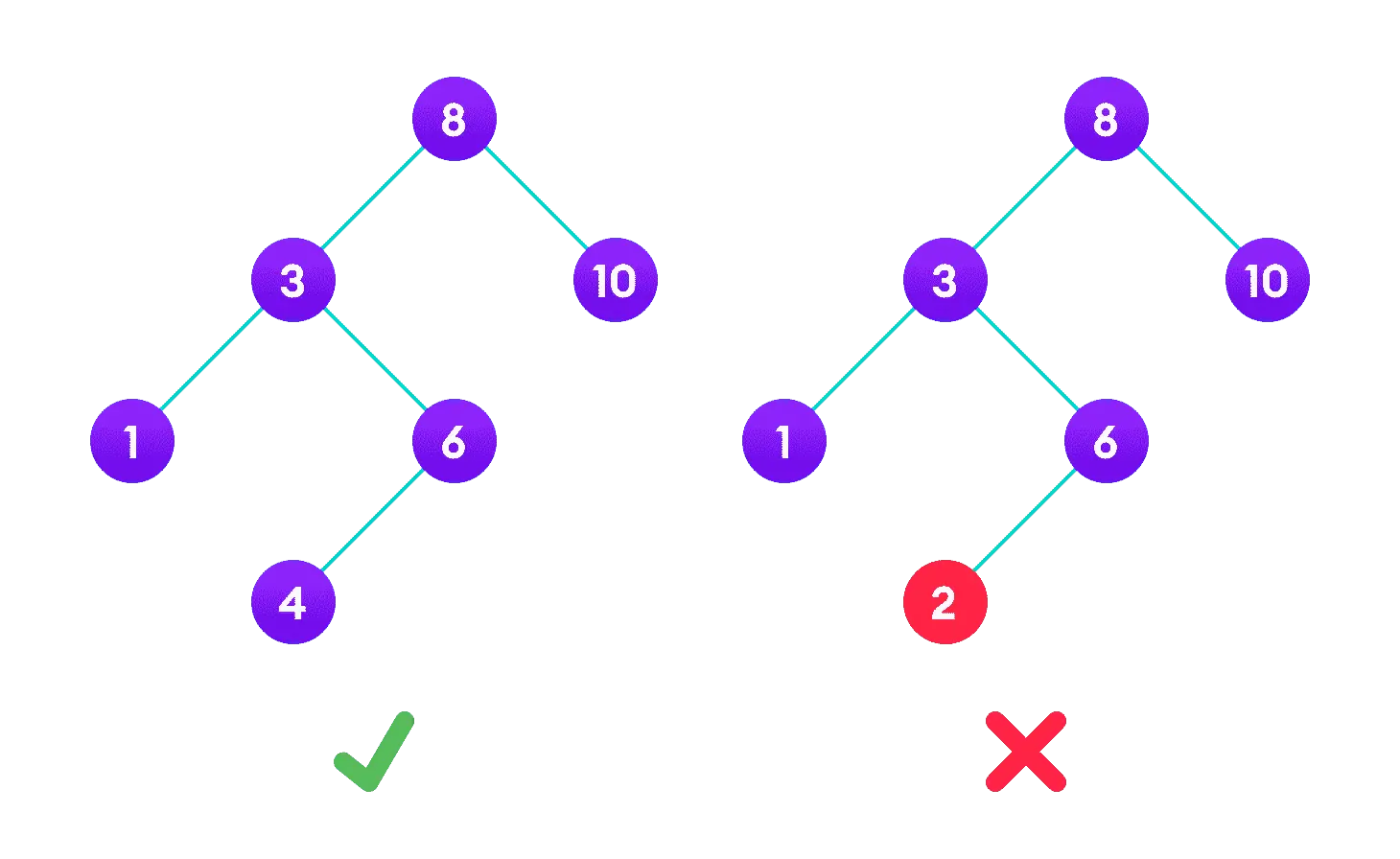
使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树 二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。 它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B 树,…...

系统接口自动化测试方案
XXX接口自动化测试方案 1、引言 1.1 文档版本 版本 作者 审批 备注 V1.0 XXXX 创建测试方案文档 1.2 项目情况 项目名称 XXX 项目版本 V1.0 项目经理 XX 测试人员 XXXXX,XXX 所属部门 XX 备注 1.3 文档目的 本文档主要用于指导XXX-Y…...
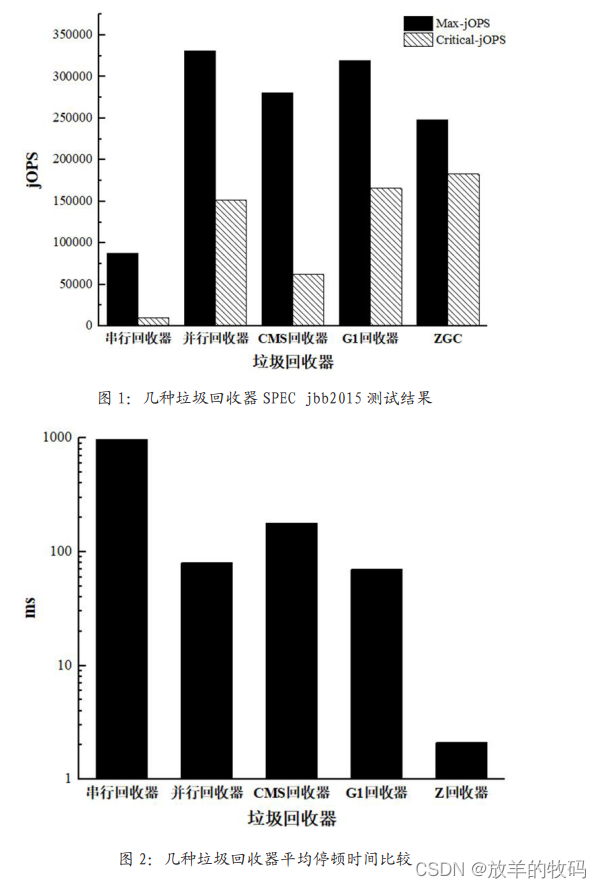
小研究 - JVM 垃圾回收方式性能研究(一)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 1 引言 2 垃圾回收算法 2.1 标记清除法 2.2…...
[LeetCode]链表相关题目(c语言实现)
文章目录 LeetCode203. 移除链表元素LeetCode237. 删除链表中的节点LeetCode206. 反转链表ⅠLeetCode92. 反转链表 II思路 1思路 2 LeetCode876. 链表的中间结点剑指 Offer 22. 链表中倒数第k个节点LeetCode21. 合并两个有序链表LeetCode86. 分隔链表LeetCode234. 回文链表Leet…...
] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现)
[深入理解NAND Flash (操作篇)] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《深入理解Flash:闪存特性与实践》 内容摘要 全文 4400 字,主要内容 复位的目的和作用? NAND Reset 种类:FFh, FCh, FAh, FDh 区别 Reset 操作步骤 和 代码实现 Read ID 操作步骤 和 代码实现 Read Uni…...

RxJava 复刻简版之二,调用流程分析之案例实现
接上篇:https://blog.csdn.net/da_ma_dai/article/details/131878516 代码节点:https://gitee.com/bobidali/lite-rx-java/commit/05199792ce75a80147c822336b46837f09229e46 java 类型转换 kt 类型: Any Object泛型: 协变: …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
