LeetCode257. 二叉树的所有路径
257. 二叉树的所有路径
文章目录
- 257. 二叉树的所有路径
- 一、题目
- 二、题解
- 方法一:深度优先搜索递归
- 方法二:迭代
一、题目
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
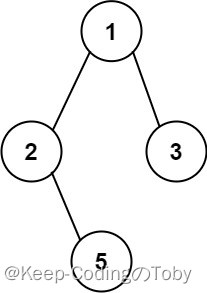
![[图片]](https://img-blog.csdnimg.cn/1cb8e903612d4a438f504b7000355c61.png)
输入:root = [1,2,3,null,5]
输出:[“1->2->5”,“1->3”]
示例 2:
输入:root = [1]
输出:[“1”]
提示:
- 树中节点的数目在范围 [1, 100] 内
- -100 <= Node.val <= 100
二、题解
方法一:深度优先搜索递归
算法思路
题目要求找出二叉树从根节点到叶子节点的所有路径。我们可以使用深度优先搜索(DFS)来遍历二叉树,并在遍历的过程中记录从根节点到当前节点的路径。当遇到叶子节点时,我们将路径添加到结果集中。
具体实现
我们可以定义一个辅助函数findPath来进行深度优先搜索。该函数的参数包括当前节点root、结果集result,以及当前路径path。
- 如果当前节点root为空,直接返回,不进行任何操作。
- 如果当前节点是叶子节点(即没有左右子节点),将当前节点的值加入到path中,并将path添加到结果集result中。
- 如果当前节点有左子节点或右子节点(可能同时有),将当前节点的值加入到path中,并加入"->"来表示路径的连接。
- 对当前节点的左子节点和右子节点分别进行递归调用findPath函数。
在主函数binaryTreePaths中,我们调用findPath函数,并将结果集作为返回值返回。
class Solution {
public:// 辅助函数,用于进行深度优先搜索遍历void findPath(TreeNode *root, vector<string>& result, string path){if(root == nullptr) return; // 若当前节点为空,则直接返回if(!root->left && !root->right){// 若当前节点是叶子节点(没有左右子节点)path += to_string(root->val); // 将当前节点的值加入到路径中result.push_back(path); // 将完整的路径添加到结果集中}else if(root->left || root->right){// 若当前节点有左子节点或右子节点(可能同时有)path += to_string(root->val); // 将当前节点的值加入到路径中path += "->"; // 用"->"连接当前节点和后续节点}findPath(root->left, result, path); // 递归处理左子节点findPath(root->right, result, path); // 递归处理右子节点} // 主函数,用于返回所有从根节点到叶子节点的路径vector<string> binaryTreePaths(TreeNode* root) {vector<string> result; // 用于存储结果集findPath(root, result, ""); // 调用辅助函数进行深度优先搜索遍历return result; // 返回结果集}
};
算法分析
- 时间复杂度:对于二叉树的每个节点,我们只访问一次,同时每次添加路径到结果集的操作的时间复杂度是O(1)。因此,整个算法的时间复杂度是O(N),其中N是二叉树的节点数量。
- 空间复杂度:递归函数调用会占用栈空间,递归的深度最坏情况下是二叉树的高度H。在最坏情况下,二叉树可能是一个斜树,高度为N,此时空间复杂度为O(N)。但在一般情况下,二叉树的高度平衡,空间复杂度接近O(logN)。
方法二:迭代
算法思路:
我们可以使用栈来辅助遍历,并在栈中同时保存当前遍历的节点和从根节点到该节点的路径。
具体实现:
- 创建一个空的字符串数组 result,用于保存所有的路径。
- 创建两个栈 TreeSt 和 PathSt,分别用于辅助二叉树的深度优先搜索和记录从根节点到当前节点的路径。
- 如果给定的 root 为空,则直接返回空的结果数组 result。
- 将 root 节点压入栈 TreeSt,并将其值转换为字符串后压入栈 PathSt。
- 进入循环,当栈 TreeSt 不为空时,执行以下操作:
- 弹出栈 TreeSt 的栈顶节点 node,同时弹出栈 PathSt 的栈顶路径 path。
- 如果 node 是叶子节点(即没有左右子节点),将 path 添加到结果数组 result 中。
- 如果 node 有右子节点,将右子节点压入栈 TreeSt,并将当前路径 path + “->” + to_string(node->right->val) 压入栈 PathSt。
- 如果 node 有左子节点,将左子节点压入栈 TreeSt,并将当前路径 path + “->” + to_string(node->left->val) 压入栈 PathSt。
- 循环结束后,返回结果数组 result。
class Solution {
public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result; // 用于保存所有从根节点到叶子节点的路径的结果数组stack<TreeNode*> TreeSt; // 辅助深度优先搜索的栈,用于遍历二叉树stack<string> PathSt; // 记录从根节点到当前节点的路径的栈if (root == nullptr) {return result; // 如果根节点为空,直接返回空的结果数组}TreeSt.push(root); // 将根节点压入栈PathSt.push(to_string(root->val)); // 将根节点值转换为字符串并压入栈while (!TreeSt.empty()) { // 当栈不为空时,进行深度优先搜索TreeNode* node = TreeSt.top(); // 弹出栈顶节点TreeSt.pop();string path = PathSt.top(); // 弹出栈顶路径PathSt.pop();if (!node->left && !node->right) { // 如果当前节点是叶子节点,将路径加入结果数组result.push_back(path);}if (node->right) { // 如果当前节点有右子节点,将右子节点和对应路径压入栈TreeSt.push(node->right);PathSt.push(path + "->" + to_string(node->right->val));}if (node->left) { // 如果当前节点有左子节点,将左子节点和对应路径压入栈TreeSt.push(node->left);PathSt.push(path + "->" + to_string(node->left->val));}}return result; // 返回所有从根节点到叶子节点的路径的结果数组}
};
算法分析:
- 时间复杂度:遍历整个二叉树的时间复杂度为O(N),其中N是二叉树的节点数。在遍历的过程中,对于每个节点,都需要将其值转换为字符串,并将其添加到结果数组中,这些操作的时间复杂度都是O(1)。因此,总体的时间复杂度为O(N)。
- 空间复杂度:栈 TreeSt 和 PathSt 最坏情况下可能同时保存所有节点,因此它们的空间复杂度为O(N)。结果数组 result 最坏情况下也可能保存所有从根节点到叶子节点的路径,因此空间复杂度为O(N)。综合考虑,总体的空间复杂度为O(N)。
相关文章:
LeetCode257. 二叉树的所有路径
257. 二叉树的所有路径 文章目录 257. 二叉树的所有路径一、题目二、题解方法一:深度优先搜索递归方法二:迭代 一、题目 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点…...

ajax、axios、fetch的区别
ajax、axios、fetch 的区别 参考答案: ajax 是指一种创建交互式网页应用的网页开发技术,并且可以做到无需重新加载整个网页的情况下,能够更新部分网页,也叫作局部更新。 使用 ajax 发送请求是依靠于一个对象,叫 XmlHtt…...

Liunx开发工具
Liunx开发工具 1.Linux编辑器-vim使用1.1vim的基本概念1.2vim的基本操作1.3命令模式命令集1.3.1光标定位1.3.2光标移动1.3.3文本复制1.3.4文本操作 1.4插入模式命令集1.5底行模式命令集 2.vim配置3.sudo配置4.Linux编辑器-gcc/g使用4.1背景知识4.2gcc如何操作 5.函数库5.1函数库…...

Docker入门之运行Nginx案例
运行镜像 如果你直接安装会比较慢, 建议参照附录内容配置镜像之后再执行 # 执行命令过程一:下载容器镜像 docker run -d nginx:latest 命令解释 docker run 启动一个容器 -d 把容器镜像中需要执行的命令以daemon(守护进程)的方式运行 nginx…...
【深度学习环境】安装anaconda、tensorflow、pycharm
目录 1.安装anaconda 2.安装tensorflow-gpu 3.安装pycharm 4.VNC操作 5.安装Pytorch PS: linux下常见的操作: 1.Linux下强制关闭程序: 2.导出环境 2.1.pip导出 2.2.conda导出 2.3.其他 3.windows下的环境安装 & pycharm远程配置 4.bash…...

mockery 模拟
composer地址:mockery/mockery - Packagist github地址:地址 文档地址:Mockery — Mockery Docs 1.0-alpha documentation 根据文档介绍,mockery是php mock对象框架。根据js的mock框架的作用,估计mockery也是通过创…...

汽车后视镜反射率检测系统
随着社会的快速发展和物质生活的提供,机动车越来越普及,道路行车安全日益重要。为了保障机动车辆和行人的安全,在行车时不断观察后方和两侧的图像尤为重要。机动车后视镜通过反射镜面可以提供在规定视野内后方和两侧的图像,从而提…...

uni-app引用外部图标库(阿里矢量图)
uni-app引用外部图标库(阿里矢量图) 作为前端程序员,nui-app是必备的,但是有时候内置的图标,组件又不完全满足,这里就可以引进外部图标,这里引用的是阿里矢量图标 第一步,在项目目…...

day49-Todo List(待办事项列表)
50 天学习 50 个项目 - HTMLCSS and JavaScript day49-Todo List(待办事项列表) 效果 index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" co…...

寻找丢失数字:数学与位运算的解密之旅
本篇博客会讲解力扣“268. 丢失的数字”的解题思路,这是题目链接。 注意进阶中的描述:你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?这里我会讲解两种思路,它们的时间复杂度是O(N),空间复杂度是O(1)…...
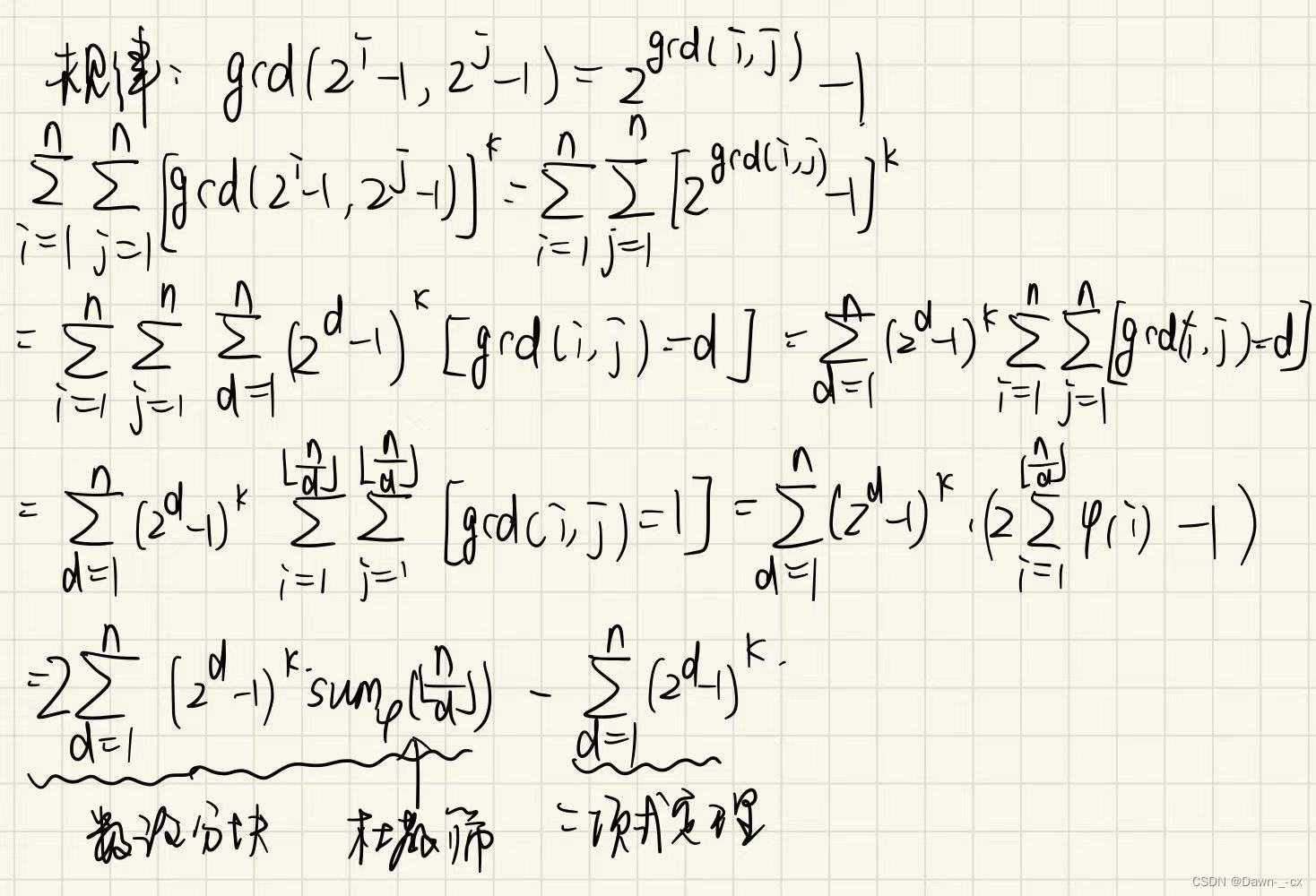
数论分块学习笔记
准备开始复习莫比乌斯反演,杜教筛这一部分,先复习一下数论分块 0.随便说说 数论分块可以计算如下形式的式子 ∑ i 1 n f ( i ) g ( ⌊ n i ⌋ ) \sum_{i1}^{n}f(i)g(\lfloor\frac{n}{i}\rfloor) ∑i1nf(i)g(⌊in⌋)。 利用的原理是 ⌊ n i ⌋ \lf…...
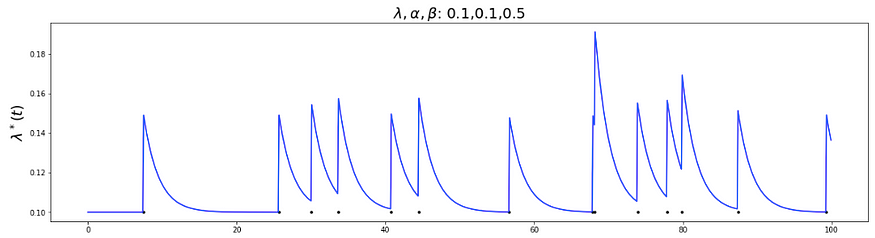
【基础理论】了解点过程
Maximum tsunami wave height generated by the 16 Sept. 2015 Chile earthquake, from the International Tsunami Information Center. Posted by Austin Elliott 一、说明 在这个世界上,会发生许多事件,其趋势可能遵循一种模式。在这篇博客中&#…...

深入理解Spring MVC中的@ResponseBody注解
引言 在现代的Web应用开发中,数据的传递和交互是不可或缺的一部分。Spring MVC作为一个强大的框架,在处理客户端请求和响应时,提供了许多注解来简化开发过程。其中,ResponseBody注解在处理方法的返回值时起到了关键作用࿰…...
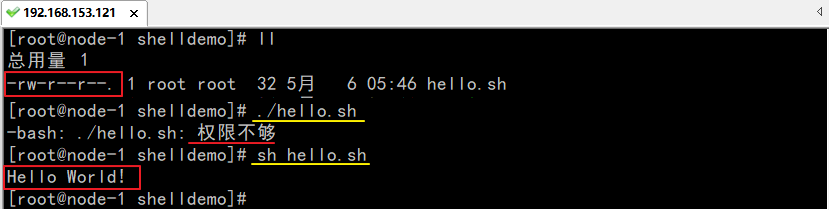
大数据学习教程:Linux高级教程(下)
四、大数据集群服务器搭建 1. 新增Linux服务器 1.1、克隆虚拟机 学习环境中,一般使用VMware虚拟机克隆Linux系统,用来进行集群服务器的搭建。 VMware支持两种类型的克隆:完整克隆、链接克隆 完整克隆是和原始虚拟机完全独立的一个复制&…...

1.Oracle建表及使用
1.概述 1. 表:用于 存储数据 -- 是我们最常见的数据库对象 2. 表设计注意事项 (1) 表设计时,尽量遵从 第三范式(3NF) (2) 名称不能超过 30 个字符 -- 超过会报错 (3) 名称只能以 字母 大头,可由数字、 _、 $…...
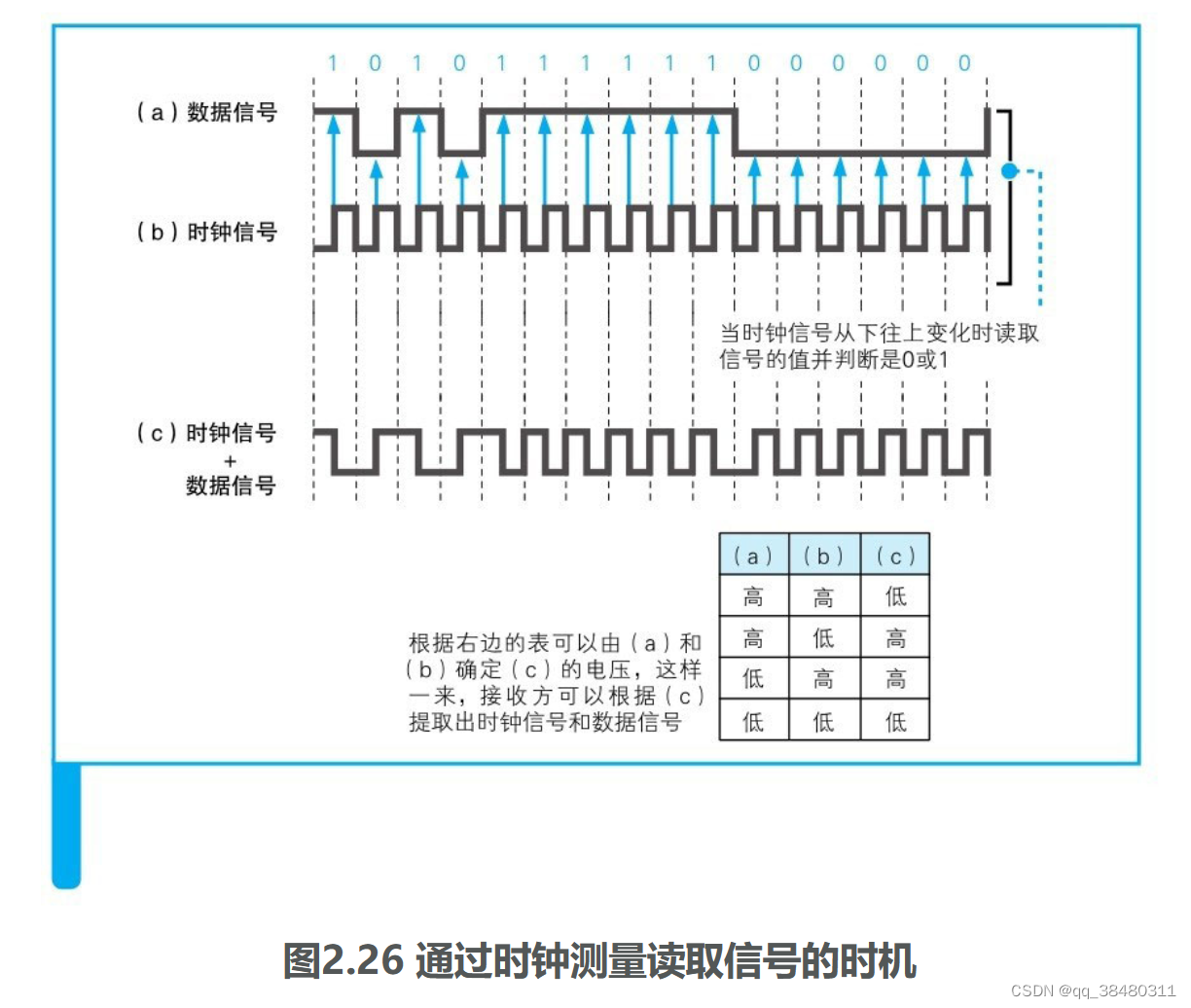
《网络是怎样连接的》(二.2)
(6条消息) 《网络是怎样连接的》(二.1)_qq_38480311的博客-CSDN博客 本文主要取材于 《网络是怎样连接的》 第二章 2.5 2.6章节。 目录 简述: 本文的主要内容是 以太网的收发操作 和 UDP协议的收发操作。 IP与以太网的包收发操作 包是什…...

MySQL加密插件安装
加密插件 查看已经安装的插件:show plugs; 增加加密插件: 登陆MySQL后,通过show variables like ‘validate%’;查看相关验证规则。 ① 在配置文件中新增,[mysqld]标签下 plugin-load-addvalidate_password.so ② 在运行时新增…...

新手入门Jenkins自动化部署入门详细教程
1. 背景 在实际开发中,我们经常要一边开发一边测试,当然这里说的测试并不是程序员对自己代码的单元测试,而是同组程序员将代码提交后,由测试人员测试; 或者前后端分离后,经常会修改接口,然后重新…...
Neural Network学习笔记4
完整的模型训练套路 train.py import torch import torchvision from torch.utils.data import DataLoader # 引入自定义的网络模型 from torch.utils.tensorboard import SummaryWriterfrom model import *# 准备数据集 train_data torchvision.datasets.CIFAR10(root"…...

[转]关于cmake --build .的理解
https://blog.csdn.net/qq_38563206/article/details/126486183 https://blog.csdn.net/HandsomeHong/article/details/120170219 cmake --build . 该命令的含义是:执行当前目录下的构建系统,生成构建目标。 cmake项目构建过程简述: 1. 首先…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
