自监督去噪:Noise2Self原理分析及实现 (Pytorch)

文章地址:https://arxiv.org/abs/1901.11365
代码地址: https://github.com/czbiohub-sf/noise2self
要点
Noise2Self方法不需要信号先验信息、噪声估计信息和干净的训练数据。唯一的假设就是噪声在测量的不同维度上表现出的统计独立性,而真实信号表现出一定的相关性。Noiser2Self根据J-invariant提出了一种噪声校正的方案,可以应用到一系列的去噪方法之中,提高这些去噪方法的效果。
文章目录
- 1. 方法原理
- 2. 实验结果
- 2.1 传统校正方法
- 2.2 高斯噪声
- 2.3 不同网络结构对比
- 3. 代码实现
- 3.1 J-invariant + 传统方法
- 3.1 J-invariant + 神经网络
- 4. 总结
1. 方法原理
如果所研究对象的空间的“潜在维度”远低于测量的维度,则可以隐式地学习该结构,对测量进行降噪,并在没有任何先验知识的情况下恢复信号,信号或噪声。
传统方法问题:
- 需要对噪声模式进行估计(如高斯噪声、结构性噪声),那么这些方法的效果就受限于对噪声模式的估计。
- 需要对信号数据的结构有先验估计,但是这会限制去噪方法迁移到其他数据集。
- 需要校准,因为平滑度、自相似性或矩阵的秩等超参数对去噪方法也会有影响
J-invariant 定义:
假设 j ∈ J j \in J j∈J, J J J是m维空间, 存在一个函数变换 f ( x ) J : R m ⇒ R m f(x)_J: R^m \Rightarrow R^m f(x)J:Rm⇒Rm。如果这个变换过程不依赖于输入的 x J x_J xJ,那么称这个函数是具有J不变性质。
换个能看懂的说法:信号本身是相关的,假设噪声是互不相关的(条件独立的),那么我们用一个方法对这个噪声图片的部分数据进行处理,这个处理结果应该是和处理全部数据效果相同的,也就是使用部分维度信息达到恢复全局的效果。(需要强调的是我自己这里也没有理解特别透彻,如果有错误可以提出大家讨论)

假设 x x x(噪声图片) 是 y y y(干净图片)的无偏估计( E [ x ∣ y ] = y E[x|y] = y E[x∣y]=y), 噪声是整个域内是条件独立的,那么有:
E ∣ ∣ f ( x ) − x ∣ ∣ 2 2 = E ∣ ∣ f ( x ) − y ∣ ∣ 2 2 + E ∣ ∣ x − y ∣ ∣ 2 2 E||f(x) - x||_2^2 = E||f(x) - y||_2^2 + E||x - y||_2^2 E∣∣f(x)−x∣∣22=E∣∣f(x)−y∣∣22+E∣∣x−y∣∣22
可以看到这里的无监督学习的损失等于 传统的监督学习的损失 加上噪声带来的偏差。
用J不变性描述一下 Noise2Noise就变为
如果现在有两个观测的噪声数据 x 1 = y + n 1 x_1 = y + n_1 x1=y+n1 , x 2 = y + n 2 x_2 = y + n_2 x2=y+n2。
观测组合: x = ( x 1 , x 2 ) x = (x_1,x_2) x=(x1,x2)
信号组合 y = ( y , y ) ∈ R 2 m y = (y,y) \in R^{2m} y=(y,y)∈R2m
如果存在 J = { J 1 , J 2 } = { { 1 , . . . , m } , { m + 1 , . . . , 2 m } } J = \{J_1,J_2\} = \{\{1,...,m\},\{m+1,...,2m\}\} J={J1,J2}={{1,...,m},{m+1,...,2m}},那么有
f J ∗ ( x ) J 2 = E [ y ∣ x 1 ] f_{J}^*(x)_{J2} = E[y|x_1] fJ∗(x)J2=E[y∣x1]
就个人理解:J-不变性就是一个假设:如果噪声是条件独立的,那么监督去噪等价于无监督去噪加上一个噪声的偏差影响。
2. 实验结果
2.1 传统校正方法
首先将J不变性应用到 传统方法中:
传统的 “median filter”是将半径范围内所有像素的点都替换为中值
这里对比的是一种“donut filter”中值滤波方法:用中值替换除了中心像素的所有位置
那么“median filter”和“donut”甜甜圈模式的滤波器,其自监督的损失分别为
∣ ∣ g r ( x ) − x ∣ ∣ 2 ||g_r(x) - x||^2 ∣∣gr(x)−x∣∣2
∣ ∣ f r ( x ) − x ∣ ∣ 2 ||f_r(x) - x||^2 ∣∣fr(x)−x∣∣2
用图绘制出来:

从上图可以看出:median滤波器监督学习的损失随着半径的增加而线性增加,而donut滤波器在r = 3的时候其损失有一个最佳值。蓝色实线和蓝色虚线的垂直距离其实表征的是噪声带来的偏差,那么我们就发现了对于传统的滤波器,我们只能够更改输入来进行调整滤波效果,但是对于donut这类具有J-invariant性质的滤波器,我们可以通过一些原则来调整滤波效果(比如这里的距离r)
那么就可以给定一个比较通用的新滤波器形式了
f θ ( x ) J : = g θ ( 1 J . s ( x ) + 1 J c . x ) J f_{\theta}(x)_J := g_{\theta}(1_J . s(x) + 1_{Jc} . x)_J fθ(x)J:=gθ(1J.s(x)+1Jc.x)J
这里的 g θ g_{\theta} gθ表示传统的滤波其, s ( x ) s(x) s(x)表示将一些像素替换为周围其他像素的值/均值的一个操作。
个人理解:和Noise2Void那种盲点去噪的感觉相同,都是将输入的某些值进行替换,然后恢复那个点的信息。如果将这种方法应用到传统方法中可以帮我们找到最佳的滤波参数。
2.2 高斯噪声

2.3 不同网络结构对比

3. 代码实现
相关代码参考: https://github.com/czbiohub-sf/noise2self
3.1 J-invariant + 传统方法
这里以使用 J-invariant 到 中值滤波为例
加载相关库和数据
import sys
sys.path.append("..")
import numpy as np
import matplotlib.pyplot as plt
from skimage.morphology import disk
from skimage.filters import gaussian, median
from skimage import data, img_as_float, img_as_ubyte
from skimage.color import gray2rgb
from skimage.util import random_noise
from skimage.metrics import structural_similarity as ssim
from skimage.metrics import peak_signal_noise_ratio as psnr
from skimage.metrics import mean_squared_error as mse
from util import plot_grid, plot_images, expand# 加载原始数据
plt.rc('figure', figsize = (5,5))
show = lambda x: plt.imshow(x, cmap=plt.cm.gray)
image = data.camera()
show(image)
plt.show()# 加噪原始数据
np.random.seed(3)
noisy_image = img_as_ubyte(random_noise(image, mode = 'gaussian', var=0.01))
show(noisy_image)
plt.show()

定义中值滤波和donut中值滤波方法(引入J-invariant)
def mask_center(x):x[len(x)//2,len(x)//2] = 0return xplot_images([1-disk(4), 1-mask_center(disk(4))])

滤波并进行对比
radii = range(1, 7)
mask_med = np.array([median(noisy_image, mask_center(disk(i))) for i in radii])
med = np.array([median(noisy_image, disk(i)) for i in radii])plt.figure(figsize=(18,6))
for i in range(1,7):plt.subplot(2,6,i)show(mask_med[i-1])plt.title("r={}".format(radii[i-1]))if i ==1:plt.ylabel("donut")for i in range(1,7):plt.subplot(2,6,6+i)show(med[i-1])if i ==1:plt.ylabel("median filter")plt.show()

统计损失及相关参考指标
def stats(im_list, noisy_img, img):img = img_as_float(img)noisy_img = img_as_float(noisy_img)im_list = [img_as_float(x) for x in im_list]loss = [mse(x, noisy_img) for x in im_list]mse_gt = [mse(x, img) for x in im_list]psnr_gt = [psnr(x, img) for x in im_list]return loss, mse_gt, psnr_gtloss_med, mse_med, psnr_med = stats(med, noisy_image, image)
loss_mask_med, mse_mask_med, psnr_mask_med = stats(mask_med, noisy_image, image)
opt = radii[np.argmin(loss_mask_med)]plt.figure(figsize=(7,5))plt.plot(radii, loss_mask_med, label = 'self-supervised, donut median', color = 'C0')
plt.plot(radii, loss_med, label = 'self-supervised, ordinary median', color = 'C1')plt.axvline(radii[np.argmin(loss_mask_med)], color='k', linestyle='--')
plt.title('Calibrating a Median Filter')plt.plot(radii, mse_mask_med, label = 'reconstruction error, donut median', color = 'C0', linestyle='--')
plt.plot(radii, mse_med, label = 'reconstruction error, ordinary median', color = 'C1', linestyle='--')
plt.ylabel('MSE')
plt.xlabel('Radius of Median Filter')plt.yticks([0.002, 0.012])
plt.ylim(0, 0.0143)
plt.legend(loc='center right')
plt.show()

加入J-invariant之后可以帮助我们找到最佳的滤波参数(此处r = 3)
3.1 J-invariant + 神经网络
加载库及数据
from util import show, plot_images, plot_tensors
from torchvision.datasets import MNIST
from torchvision import transforms
from torch.utils.data import Datasetmnist_train = MNIST(root='/data/mnist/', download = True,transform = transforms.Compose([transforms.ToTensor(),]), train = True)mnist_test = MNIST('/data/mnist/', download = True,transform = transforms.Compose([transforms.ToTensor(),]), train = False)
定义加噪方法
from torch import randn
def add_noise(img):return img + randn(img.size())*0.4class SyntheticNoiseDataset(Dataset):def __init__(self, data, mode='train'):self.mode = modeself.data = datadef __len__(self):return len(self.data)def __getitem__(self, index):img = self.data[index][0]return add_noise(img), img
noisy_mnist_train = SyntheticNoiseDataset(mnist_train, 'train')
noisy_mnist_test = SyntheticNoiseDataset(mnist_test, 'test')
noisy, clean = noisy_mnist_train[0]
plot_tensors([noisy[0], clean[0]], ['Noisy Image', 'Clean Image'])

加mask也就是加盲点,需要恢复的也是这些盲点的信息
class Masker():"""Object for masking and demasking"""def __init__(self, width=3, mode='zero', infer_single_pass=False, include_mask_as_input=False):self.grid_size = widthself.n_masks = width ** 2self.mode = modeself.infer_single_pass = infer_single_passself.include_mask_as_input = include_mask_as_inputdef mask(self, X, i):phasex = i % self.grid_sizephasey = (i // self.grid_size) % self.grid_sizemask = pixel_grid_mask(X[0, 0].shape, self.grid_size, phasex, phasey)mask = mask.to(X.device)mask_inv = torch.ones(mask.shape).to(X.device) - maskif self.mode == 'interpolate':masked = interpolate_mask(X, mask, mask_inv)elif self.mode == 'zero':masked = X * mask_invelse:raise NotImplementedErrorif self.include_mask_as_input:net_input = torch.cat((masked, mask.repeat(X.shape[0], 1, 1, 1)), dim=1)else:net_input = maskedreturn net_input, maskdef __len__(self):return self.n_masksdef infer_full_image(self, X, model):if self.infer_single_pass:if self.include_mask_as_input:net_input = torch.cat((X, torch.zeros(X[:, 0:1].shape).to(X.device)), dim=1)else:net_input = Xnet_output = model(net_input)return net_outputelse:net_input, mask = self.mask(X, 0)net_output = model(net_input)acc_tensor = torch.zeros(net_output.shape).cpu()for i in range(self.n_masks):net_input, mask = self.mask(X, i)net_output = model(net_input)acc_tensor = acc_tensor + (net_output * mask).cpu()return acc_tensordef pixel_grid_mask(shape, patch_size, phase_x, phase_y):A = torch.zeros(shape[-2:])for i in range(shape[-2]):for j in range(shape[-1]):if (i % patch_size == phase_x and j % patch_size == phase_y):A[i, j] = 1return torch.Tensor(A)def interpolate_mask(tensor, mask, mask_inv):device = tensor.devicemask = mask.to(device)kernel = np.array([[0.5, 1.0, 0.5], [1.0, 0.0, 1.0], (0.5, 1.0, 0.5)])kernel = kernel[np.newaxis, np.newaxis, :, :]kernel = torch.Tensor(kernel).to(device)kernel = kernel / kernel.sum()filtered_tensor = torch.nn.functional.conv2d(tensor, kernel, stride=1, padding=1)return filtered_tensor * mask + tensor * mask_invmasker = Masker(width = 4, mode='interpolate')
net_input, mask = masker.mask(noisy.unsqueeze(0), 0)
plot_tensors([mask, noisy[0], net_input[0], net_input[0] - noisy[0]],["Mask", "Noisy Image", "Neural Net Input", "Difference"])
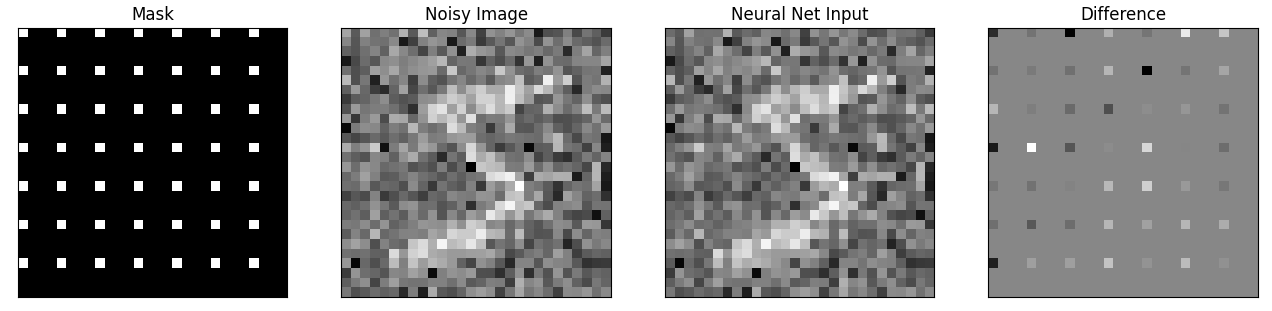
加载网络模型和进行训练
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn import MSELoss
from torch.optim import Adam
from torch.utils.data import DataLoader
from tqdm import tqdm
from models.modules import ConvBlockclass BabyUnet(nn.Module):def __init__(self, n_channel_in=1, n_channel_out=1, width=16):super(BabyUnet, self).__init__()self.pool1 = nn.MaxPool2d(kernel_size=2)self.pool2 = nn.MaxPool2d(kernel_size=2)self.up1 = lambda x: F.interpolate(x, mode='bilinear', scale_factor=2, align_corners=False)self.up2 = lambda x: F.interpolate(x, mode='bilinear', scale_factor=2, align_corners=False)self.conv1 = ConvBlock(n_channel_in, width)self.conv2 = ConvBlock(width, 2*width)self.conv3 = ConvBlock(2*width, 2*width)self.conv4 = ConvBlock(4*width, 2*width)self.conv5 = ConvBlock(3*width, width)self.conv6 = nn.Conv2d(width, n_channel_out, 1)def forward(self, x):c1 = self.conv1(x)x = self.pool1(c1)c2 = self.conv2(x)x = self.pool2(c2)x = self.conv3(x)x = self.up1(x)x = torch.cat([x, c2], 1)x = self.conv4(x)x = self.up2(x)x = torch.cat([x, c1], 1)x = self.conv5(x)x = self.conv6(x)return x
model = BabyUnet()
loss_function = MSELoss()
optimizer = Adam(model.parameters(), lr=0.001)data_loader = DataLoader(noisy_mnist_train, batch_size=32, shuffle=True)pbar = tqdm(data_loader)for i, batch in enumerate(pbar):noisy_images, clean_images = batchnet_input, mask = masker.mask(noisy_images, i)net_output = model(net_input)loss = loss_function(net_output*mask, noisy_images*mask)optimizer.zero_grad()loss.backward()optimizer.step()pbar.set_description("Iter:{},loss:{}".format(i,loss.item()))# if i % 10 == 0:# print("Loss (", i, "): \t", round(loss.item(), 4))if i == 100:break
测试训练效果
test_data_loader = DataLoader(noisy_mnist_test,batch_size=32,shuffle=False,num_workers=3)
i, test_batch = next(enumerate(test_data_loader))
noisy, clean = test_batch
simple_output = model(noisy)
invariant_output = masker.infer_full_image(noisy, model)
idx = 3
plot_tensors([clean[idx], noisy[idx], simple_output[idx], invariant_output[idx]],["Ground Truth", "Noisy Image", "Single Pass Inference", "J-Invariant Inference"])

盲点网络训练后使用不同的输入(加盲点或者不加)得到的效果有些许差别,但是整体的去噪效果还可以。
4. 总结
- 引入J-invariant的概念到去噪工作之中,通过测试对比发现这种方法的自监督比传统方法有更好的效果,可以帮助传统方法寻找最佳的调整参数
- J-invariant的思路可以应用到传统去噪方法中或者先前的无监督、自监督学习工作之中,提高效果。(对比了Noise2Noiser和Noiser2Void方法)
- 和Noise2Void有异曲同工之妙,分析原理都是使用盲点网络的思想对输入数据进行mask,然后使用网络恢复这些盲点位置的信息。所以也存在和盲点网络相同的问题
- 损失了盲点位置的信息
- 盲点网络的假设:噪声是条件不相关的,信号是相关的;对于结构性的噪声的效果会较差。
- 噪声零均值假设等假设限制了该方法应用到实际数据之中。
相关文章:

自监督去噪:Noise2Self原理分析及实现 (Pytorch)
文章地址:https://arxiv.org/abs/1901.11365 代码地址: https://github.com/czbiohub-sf/noise2self 要点 Noise2Self方法不需要信号先验信息、噪声估计信息和干净的训练数据。唯一的假设就是噪声在测量的不同维度上表现出的统计独立性,而真实信号表现出一定的…...

docker容器学习笔记1
docker容器是干什么用的 docker就是一个轻量级的虚拟机,是一个容器,隔离性好,能够确保环境的统一,有效利用系统资源,轻松迁移和拓展。简单的可以理解为容器就是一个小型功能齐全的虚拟机。 实际上是如何使用的呢&…...

线程魔法:用Spring Boot的@Async注解开启异步世界
在现代的应用程序开发中,异步调用已成为提高性能和响应性的重要策略之一。通过使用Spring Boot框架,我们可以轻松地实现异步调用,从而在处理请求时能够同时执行耗时的操作,如发送电子邮件、处理文件等,而不会阻塞主线程…...
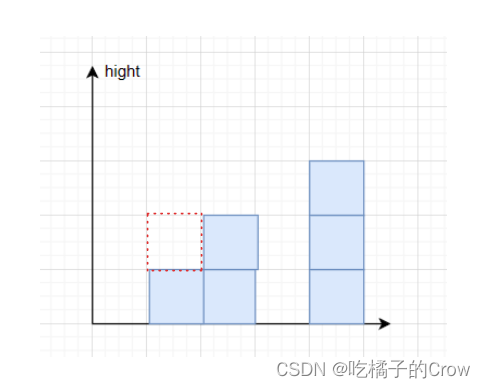
面试热题(接雨水问题)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 我们看到题的第一步,永远是对入参进行判断 public int trap(int[] height) {if (height null) {return 0;}...} 但是我们想想看,接…...
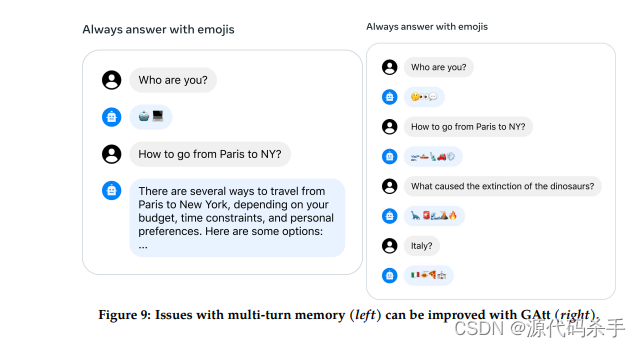
Meta AI研究团队新AI模型: Llama 2 大语言模型
Llama是Facebook Research团队开发的基础语言模型集,旨在提供广泛的语言理解能力。它基于转换器架构,参数范围从7B到65B。通过使用Llama模型,研究人员和开发人员可以构建更先进的自然语言处理系统。您可以在GitHub上找到相关的代码和资源&…...

CSS水平垂直居中
1.利用定位 margin:auto 2.flex布局 3.grid布局 一、利用positionmargin:auto <style>.outer {position: relative; /*父亲相对定位*/width: 200px;height: 200px;background-color: red;}.inner {position: absolute; /*儿子绝对定位*/top: 0;bottom: 0;left: 0;ri…...

Yolov8-pose关键点检测:模型部署篇 | yolov8-pose.onnx python推理
💡💡💡本文解决什么问题:Yolov8-pose关键点训练得到的模型转换成onnx格式在python下完成推理 Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_63774211/category_12398833.html ✨✨✨手把手教你从数据标记到生成适合Yolov8-pose的yolo数据集; 🚀🚀�…...
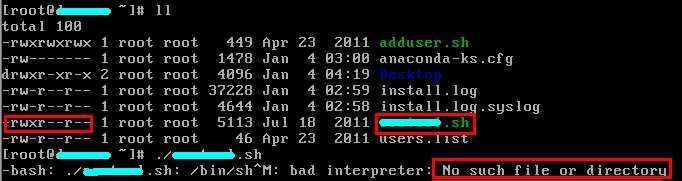
Linux中提示No such file or directory解决方法
说明: 在linux下,./xxx.sh执行shell脚本时会提示No such file or directory。但shell明明存在,为什么就是会提示这个呢? 这种其实是因为编码方式不对,如你在win下编辑sh,然后直接复制到linux下面 实现&…...

Sklearn-使用SVC对iris数据集进行分类
Sklearn-使用SVC对iris数据集进行分类 iris数据集的加载训练svc模型输出混淆矩阵和分类报告使用Pipeline管道完成固定操作不使用Pipeline使用Pipeline 使用SVC对iris数据集进行分类预测 涉及内容包含: 数据集的加载,训练集和测试集的划分训练svc模型,对测试集的预测…...

项目经理必读:领导风格对项目成功的关键影响
引言 项目经理作为一个领导者的角色,他们需要协调各方资源,管理团队,推动项目的进行。为了完成这些任务,项目经理必须具备各种领导风格的灵活性,以应对项目中的各种变数和挑战。在这篇文章中,我们将讨论领…...
行业追踪,2023-08-04
自动复盘 2023-08-04 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
双链表(带哨兵位头节点)
目录 编辑 双链表的初始化: 双链表的打印: 双链表的尾插: 双链表的头插: 双链表的尾删: 双链表的头删: 双链表pos位置之前的插入: 双链表pos位置的删除: 关于顺序表和链表…...
)
MySQL - LOAD DATA LOCAL INFILE将数据导入表中和 INTO OUTFILE (速度快)
文章目录 一、语法介绍二、数据分隔符介绍 :换行符说明: 三、示例LOAD DATA LOCAL INFILEINTO OUTFILE 总结 一、语法介绍 LOAD DATA[LOW_PRIORITY | CONCURRENT] [LOCAL]INFILE file_name[REPLACE | IGNORE]INTO TABLE tbl_name[PARTITION (partition_name [, par…...

String ,StringBulider ,StringBuffer
面试指北149 知乎 StringBuffer和StringBuilder区别详解(Java面试)_stringbuffer和stringbuilder的区别_辰兮要努力的博客-CSDN博客...

阶段总结(linux基础)
目录 一、初始linux系统 二、基本操作命令 三、目录结构 四、文件及目录管理命令 查看文件内容 创建文件 五、用户与组管理 六、文件权限与压缩管理 七、磁盘管理 八、系统程序与进程管理 管理机制 文件系统损坏 grub引导故障 磁盘资源耗尽 程序与进程的区别 查…...
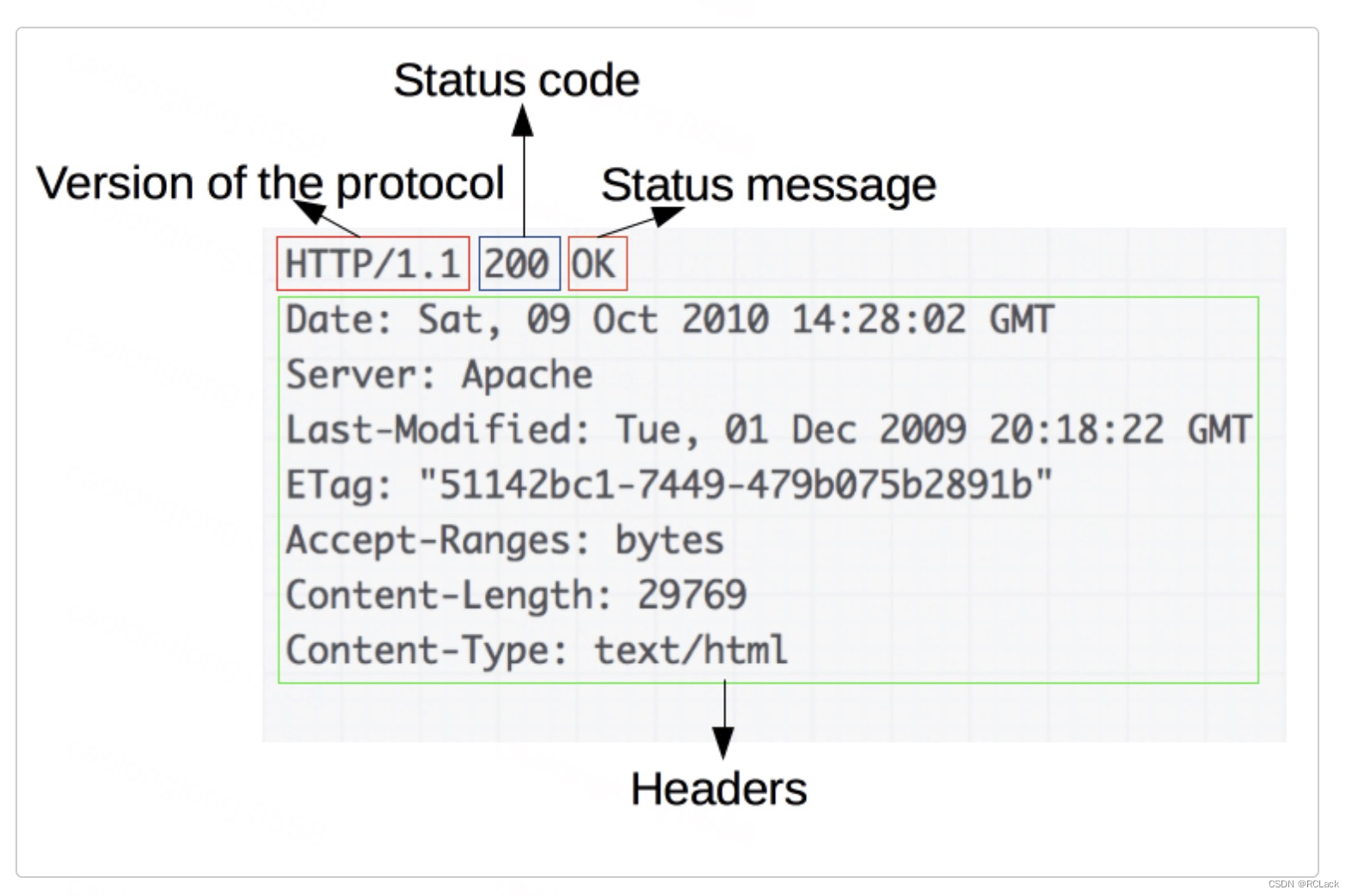
HTTP(超文本传输协议)学习
关于HTTP补学 一、HTTP能干什么 通过下图能够直观的看出:“交换数据 ” 二、HTTP请求例子 一个 HTTP 方法,通常是由一个动词,像 GET、POST 等,或者一个名词,像 OPTIONS、HEAD 等,来定义客户端执行的动作。…...
)
23年7月工作笔记整理(前端)
目录 一、js相关二、业务场景学习 一、js相关 1.js中Number类型的最大值常量:Number.MAX_VALUE,最小值常量:Number.MIN_VALUE 2.巩固一下reduce语法:reduce(function(初始值或方法的返回值,当前值,当前值的索引,要累加的初始值))…...
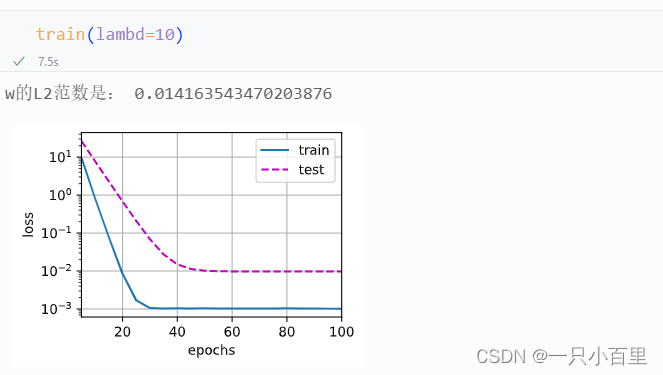
pytorch学习——正则化技术——权重衰减
一、概念介绍 权重衰减(Weight Decay)是一种常用的正则化技术,它通过在损失函数中添加一个惩罚项来限制模型的复杂度,从而防止过拟合。 在训练参数化机器学习模型时, 权重衰减(weight decay)是…...
iTOP-RK3588开发板Ubuntu 系统交叉编译 Qt 工程-命令行交叉编译
使用源码 rk3588_linux/buildroot/output/rockchip_rk3588/host/bin/qmake 交叉编译 QT 工程。 最后烧写编译好的 buildroot 镜像,将编译好的 QT 工程可执行程序在 buildroot 系统上运行。 交叉编译 QT 工程如下所示,首先进入 QLed 的工程目录下。 然后…...
Java进阶——数据结构与算法之哈希表与树的入门小结(四)
文章大纲 引言一、哈希表1、哈希表概述2、哈希表的基本设计思想3、JDK中的哈希表的设计思想概述 二、树1、树的概述2、树的特点3、树的相关术语4、树的存储结构4.1、双亲表示法4.2、孩子兄弟表示法:4.3、孩子表示法:4.4、双亲孩子表示法 三、二叉树1、二…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
