2023年第三届工业自动化、机器人与控制工程国际会议 | IET独立出版 | EI检索

会议简介 Brief Introduction
2023年第三届工业自动化、机器人与控制工程国际会议(IARCE 2023)
会议时间:2023年10月27 -30日
召开地点:中国·成都
大会官网:www.iarce.org
2023年第三届工业自动化、机器人与控制工程国际会议(IARCE 2023)将围绕“工业自动化、机器人与控制工程”的最新研究领域而展开,为研究人员、工程师、专家学者以及行业专业人士提供一个交流与探讨最新研究成果的平台,并为与会者们交流新的思想和应用经验建立业务或研究关系。本次会议将于2023年10月27至30日在中国成都召开,在会议期间您将有机会聆听到行业前沿的学术报告,见证该领域的成果与进步。现热忱欢迎从事相关技术研究的专家学者及学生踊跃投稿并参加本次会议。
合作单位 Cooperation
承办单位:西南交通大学、北京航空航天大学、北京邮电大学



协办单位:北京理工大学、华东理工大学、重庆大学



重要信息 Highlights
截稿时间:2023年9月23日
录用通知:投稿后两周内
检索信息:Ei Compendex检索
出版信息 Publication
所有被大会接收的论文将收录至会议在线论文集并提交至IET Conference Proceedings进行出版,见刊后将提交至EI Compendex等主流数据库检索。优秀论文将被推荐至国际期刊上发表。


主旨报告 keynote Speech

Prof. Jianrong Tan
Institute of Design Engineering School of Mechanical Engineering, Zhejiang University, China
Academician of Chinese Academy of Engineering(中国工程院院士)

Prof. Tingwen Huang
Texas A&M University, Qatar
Fellow of TWAS, Fellow of IEEE and IAPR

Prof. Guangbin Huang
Nanyang Technological University, Singapore
IEEE Fellow

Assoc. Prof. Wei Pan
University of Manchester, UK
会议征稿主题 Call for Paper
IARCE 2023主题涵盖工业自动化、机器人与控制工程及其相关领域,横跨理论基础和应用研究。所征集的主题包括但不限于:
系统工程理论与技术
控制理论与技术
控制系统与应用
系统建模理论、仿真技术与虚拟现实
自动化检测技术与装置
导航、制导与控制
人工智能驱动的自动化
知识自动化
新兴领域的自动化理论与技术
机器人学与智能系统
工业机器人
机器人集群
协作机器人
医疗与康复机器人
服务机器人
仿生机器人
空间机器人
机器人感知、认知、决策
人机交互与人因工程
复杂性科学与人工智能理论
生物、医学信息系统与技术
传感器网络与物联网
智能制造与工业智能
故障诊断与容错控制
微纳机电器件与控制系统
模糊系统与模糊控制
网络协同与自主控制
信息系统与系统安全
软件控制论
信号处理与信息融合
多智能体系统与分布式控制
博弈论
脑机接口与生机电一体化
情感计算
自然语言理解
环境适应性设计理论与方法
伦理与安全
云计算与计算智能
神经网络与深度学习
机器感知与机器视觉
模式识别与数据挖掘
知识表示与处理
动态规划与强化学习
智能系统与人工智能安全
数据科学与大数据计算
新型计算及其应用基础
认知与神经科学启发的人工智能
生物信息计算与数字健康
社会与经济系统调控
教育信息科学与技术
交叉学科中的人工智能问题
更多征稿主题请访问:IARCE 2023-CFP
注册说明 Registration Instruction
1. 所有参会者都应填写《注册表》。付款成功后,请将填写好的表格发送到会议邮箱。如需中文注册表,请联系contact@iarce.org。
2. 要求在注册截止日前将终稿、注册表和付款发送到会议邮箱。
3. 通过我们的在线支付系统(点击)支付注册费,也可以在注册表上找到此链接。
4. 将您填写好的报名表、付款凭证和其他相关文件发送到会议邮箱:contact@iarce.org。
5. 至少有一位论文作者应注册参会,并且至少有一位作者必须在会议上发表论文。否则,该论文将不被列入会议论文集。
6. 在收到注册费全额和提交注册表后,注册才会被确认。我们将向注册者的邮箱发送一封电子邮件,确认注册成功。请在会议现场出示确认函,办理所有注册手续。
7. 请在会议日期前两个月与会议组织者确认会议形式(线上或线下)。由于会议组织者通常不会为参会者预定酒店,建议现场参会人员自行提前预订现场(线下)会议的酒店。
8. 其他合著者和陪同人员可以作为听众注册。
参会方式 Type of Attendance
1.作者参会:一篇会议录用文章允许一名作者参会;
2.主讲嘉宾:申请主题演讲,由会务组审核;
3.口头演讲:申请口头报告,时间为15分钟;
4.海报参会:申请海报参会,依照官网模板准备海报,再录制5分钟视频;
5.视频参会:录制15分钟个人视频即可;
6.听众参会:不投稿仅参会,可参与问答,也可演讲及展示。
投稿方式 Submission Method
1. 会议邮箱:contact@iarce.org
2. CMT在线投稿:Submission
请作者按照官网模板格式进行排版。排版好的论文全稿(word+pdf版)发送至CMT在线系统或者会议邮箱。
投稿要求 Submission Type
1. 大会官方语言为英语,必须为全英文稿件,且应具有学术或实用价值,未在国内外学术期刊或会议发表过;
2. 保证文章原创性,未在国内外公开刊物或其它学术会议上发表过;
3. 文章篇幅一般在5-12页之间,不少于5页,含公式图表等,超过6页将收取超页费;
4. 作者可通过iThenticate或其他查询系统自费查重,重复率不得超过20%,由文章重复率引起的被拒稿将由作者自行承担责任;
5. 文章录用:若您的文章被录用,我们将以邮件形式通知您,您将收到以下文件:录用通知、审稿意见表、中文注册表。
联系我们 Contact us
会议秘书:李女士
会议官网:www.iarce.org
会议邮箱:contact@iarce.org
相关文章:

2023年第三届工业自动化、机器人与控制工程国际会议 | IET独立出版 | EI检索
会议简介 Brief Introduction 2023年第三届工业自动化、机器人与控制工程国际会议(IARCE 2023) 会议时间:2023年10月27 -30日 召开地点:中国成都 大会官网:www.iarce.org 2023年第三届工业自动化、机器人与控制工程国际…...
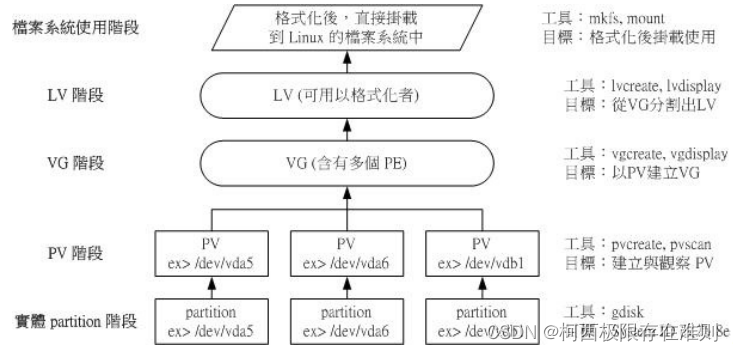
14.2.2 【Linux】software, hardware RAID
磁盘阵列分为硬件与软件。所谓的硬件磁盘阵列是通过磁盘阵列卡来达成阵列的目的。磁盘阵列卡上面有一块专门的芯片在处理 RAID 的任务,因此在性能方面会比较好。在很多任务 (例如 RAID 5 的同位检查码计算) 磁盘阵列并不会重复消耗原本系统的…...
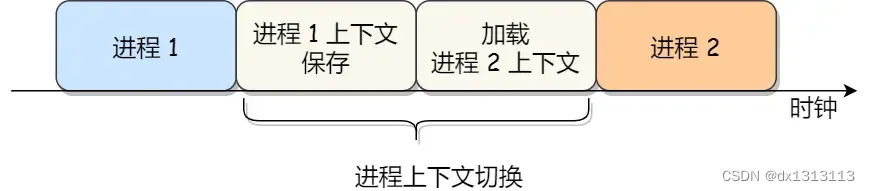
(学习笔记-进程管理)进程
进程 我们编写的代码只是一个存储在硬盘的静态文件,通过编译后会生成二进制可执行文件,当我们运行这个可执行文件后,它会被装载到内存中,接着CPU会执行程序中的每一条指令,那么这个运行中的程序就被称为进程。 现在我…...
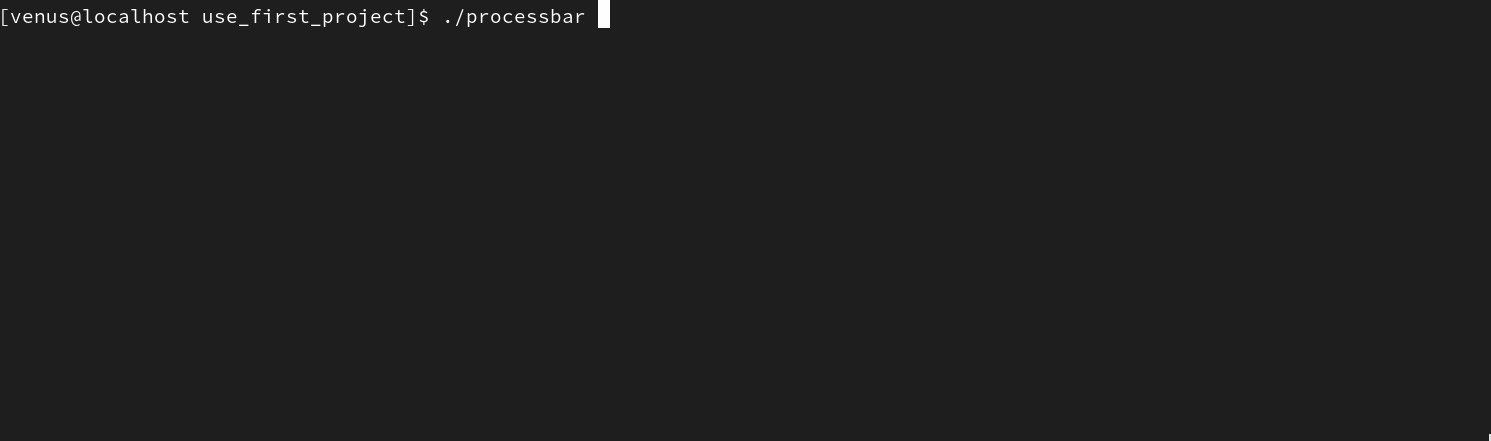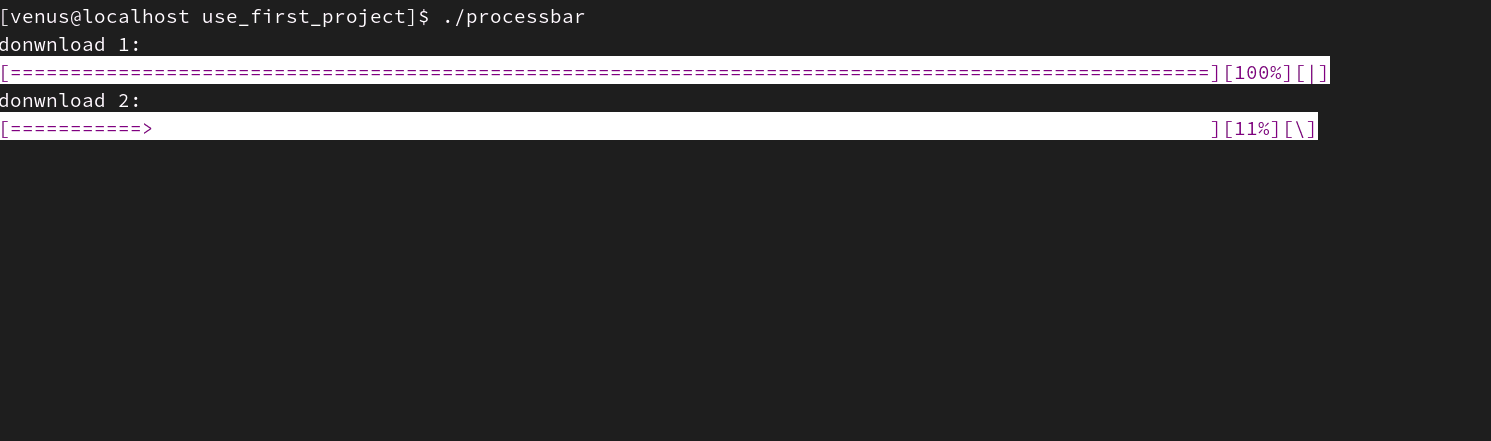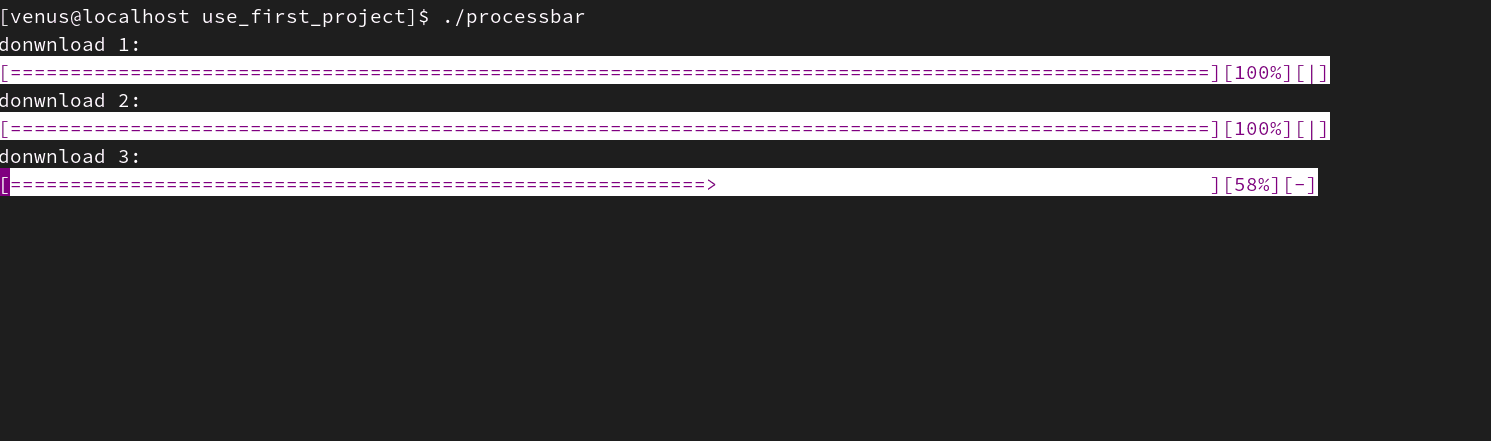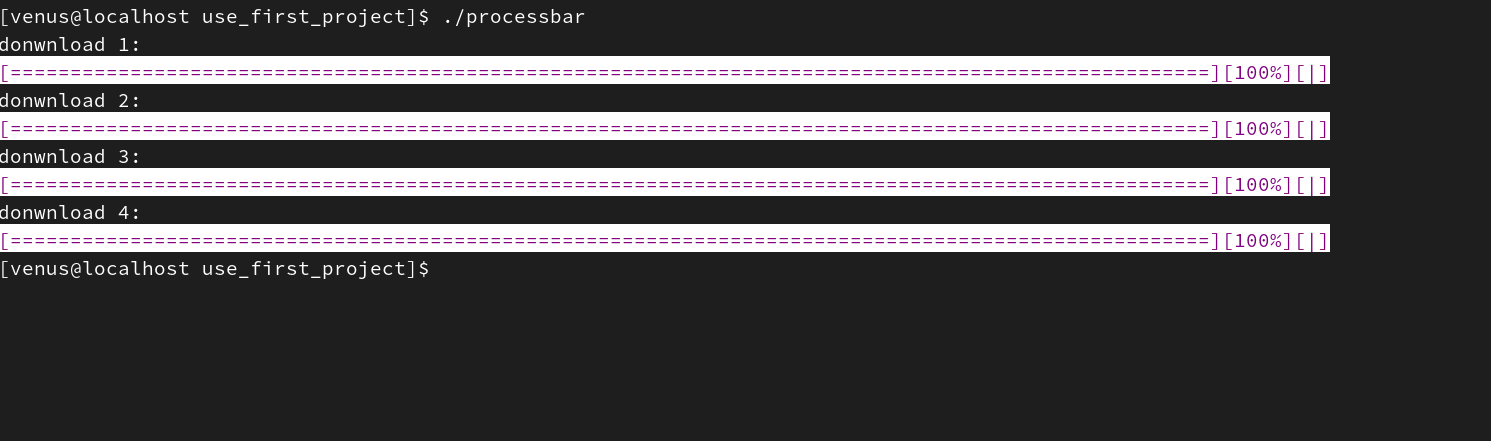
《Linux从练气到飞升》No.07 Linux第一个小程序-进度条的实现
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...
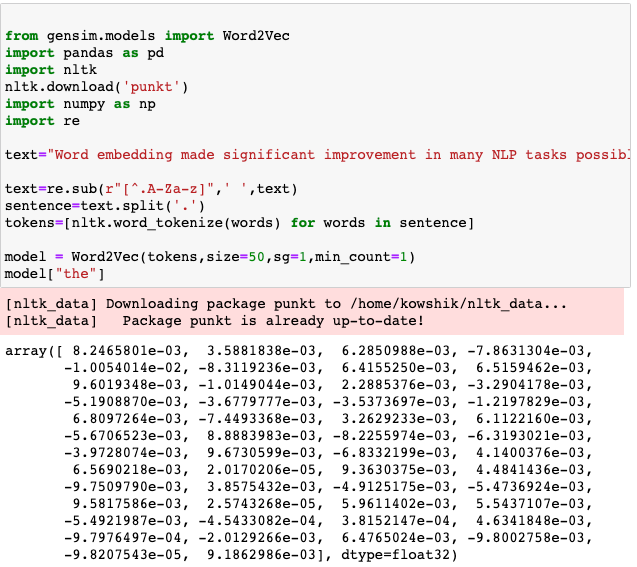
【NLP概念源和流】 04-过度到RNN(第 4/20 部分)
接上文 【NLP概念源和流】 03-基于计数的嵌入,GloVe(第 3/20 部分) 一、说明 词嵌入使许多NLP任务有了显著的改进。它对单词原理图的理解以及将不同长度的文本表示为固定向量的能力使其在许多复杂的NLP任务中非常受欢迎。大多数机器学习算法可以直接应用于分类和回归任务的…...

企业上云实施路线图
企业上云步骤主要分为规划、设计、实施、验证、运维五个阶段。https://articles.e-works.net.cn/cloud/article144684.htm...

docker系列--解决hyper-v导致docker无法启动问题
一、问题 windows docker desktop 启动报错异常,导致docker无法启动成功 我们看到问题出在hyper-v的问题上,搜索解决方法,官网常见问题如下 Overview | Docker Documentation 二、解决 Hyper-V 已安装并正常工作 在BIOS中启用虚拟化 Wind…...
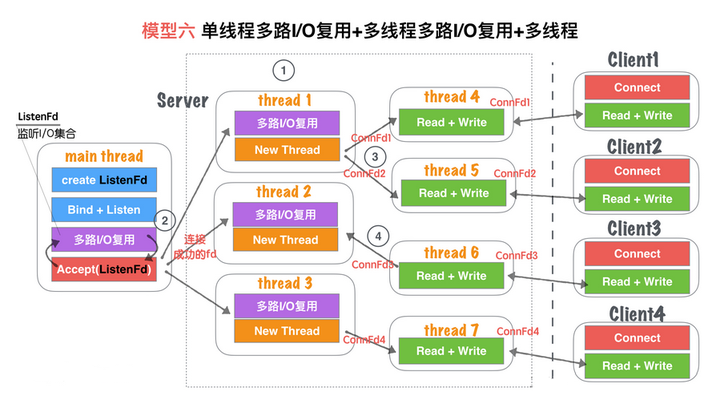
socket server服务器开发常见的并发模型
两种高效的事件处理模式 服务器程序通常需要处理三类事件:I/O 事件、信号及定时事件。有两种高效的事件处理模式:Reactor和 Proactor,同步 I/O 模型通常用于实现Reactor 模式,异步 I/O 模型通常用于实现 Proactor 模式。 无论是 …...

怎么修改pdf文件中的文字?分享几种编辑方法
怎么修改pdf文件中的文字?PDF格式的文件通常具有很高的可读性和稳定性,但是如果需要修改其中的文字,就需要使用专门的PDF编辑器。本文将介绍几种PDF编辑的方法,下面就跟着我一起来看看这几款工具吧。 方法一:使用迅捷P…...
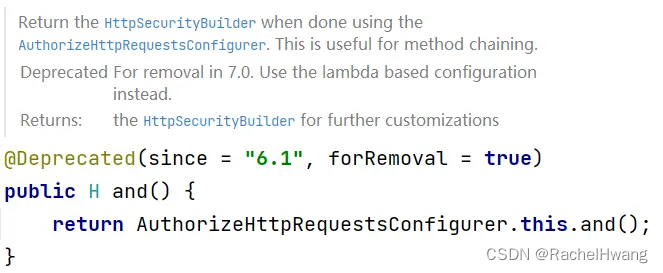
spring — Spring Security 5.7与6.0差异性对比
1. spring security Spring Security 是一个提供身份验证、授权和针对常见攻击保护的框架。 凭借对保护命令式和反应式应用程序的一流支持,它成为基于Spring的标准安全框架。 Spring Security 在最近几个版本中配置的写法都有一些变化,很多常见的方法都…...

道本科技受邀参加建筑产业互联网推动建筑产业现代化体系构建座谈会,以数字化产品为建筑行业注入新动能!
2023年7月底,道本科技作为中国建筑业协会合作伙伴,受邀参加了建筑产业互联网推动建筑产业现代化体系构建座谈会。在这次座谈会上,道本科技旗下产品“合规数”“合同智能审查”和“智合同范本库”被中国建筑(中小企业)产…...

数据结构----效率问题
数据结构----效率问题 一.衡量效率 1.衡量效率的两个维度 1.时间维度:时间复杂度:Time Complexity 时间复杂度是代码总的运行次数(粗糙) 2.空间维度:空间复杂度:Space Complexity 空间复杂度是额外申…...
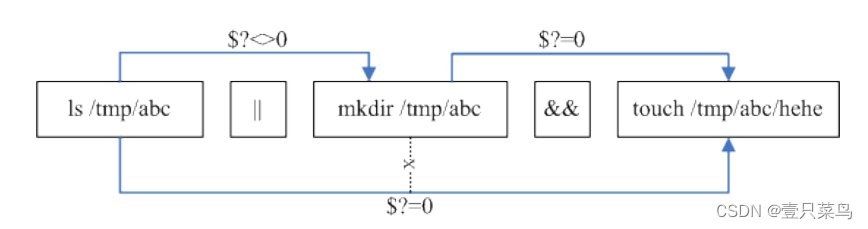
【BASH】回顾与知识点梳理(五)
【BASH】回顾与知识点梳理 五 五. 数据流重导向5.1 什么是数据流重导向standard output 与 standard error output/dev/null 垃圾桶黑洞装置与特殊写法standard input : < 与 << 5.2 命令执行的判断依据: ; , &&, ||cmd ; cmd (不考虑指…...

PCL点云处理之最小二乘空间直线拟合(3D) (二百零二)
PCL点云处理之最小二乘空间直线拟合(3D) (二百零二) 一、算法简介二、实现代码三、效果展示一、算法简介 对于空间中的这样一组点:大致呈直线分布,散乱分布在直线左右, 我们可采用最小二乘方法拟合直线,更进一步地,可以通过点到直线的投影,最终得到一组严格呈直线分布…...

大数据课程G1——Hbase的概述
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解HIve的概念; ⚪ 了解HIve与数据库的区别; ⚪ 了解HIve的特点; 一、简介 1. 概述 1. HBase原本是由Yahoo!公司开发后来贡献给了…...

第三章 图论 No.2单源最短路之虚拟源点,状压最短路与最短路次短路条数
文章目录 1137. 选择最佳线路1131. 拯救大兵瑞恩1134. 最短路计数383. 观光 dp是特殊的最短路,是无环图(拓扑图)上的最短路问题 1137. 选择最佳线路 1137. 选择最佳线路 - AcWing题库 // 反向建图就行 #include <iostream> #include…...

汉诺塔问题
一本通1205:汉诺塔问题 【题目描述】 约19世纪末,在欧州的商店中出售一种智力玩具,在一块铜板上有三根杆,最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上,条件…...
Java on Azure Tooling 6月更新|标准消费和专用计划及本地存储账户(Azurite)支持
作者:Jialuo Gan - Program Manager, Developer Division at Microsoft 排版:Alan Wang 大家好,欢迎阅读 Java on Azure 工具的六月更新。在本次更新中,我们将介绍 Azure Spring Apps 标准消费和专用计划支持以及本地存储账户&…...
-网络嗅探-黑盒监控)
Prometheus(八)-网络嗅探-黑盒监控
介绍 Blackbox Exporter是Prometheus社区提供的官方黑盒监控解决方案,其允许用户通过:HTTP、HTTPS、DNS、TCP以及ICMP的方式对网络进行探测。用户可以直接使用go get命令获取Blackbox Exporter源码并生成本地可执行文件: go get prometheus…...

modbus TCP 通信测试
modbus TCP 通信测试 读取单个或多个线圈 发送指令:00 00 00 00 00 06 00 01 03 10 00 08 00 00 00 00 00 06 00 01 03 10 00 08 事务 处理 标识 协议 标识 长度 单元 标识 功能码 起始 线圈 地址 线圈 个数 06:后面的字节长度。 01&am…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
