vue diff 双端比较算法
文章目录
- 双端指针
- 比较策略
- 命中策略四
- 命中策略二
- 命中策略三
- 命中策略一
- 未命中四种策略,遍历旧节点列表
- 新增情况一
- 新增情况二
- 删除节点
- 双端比较的优势
双端指针
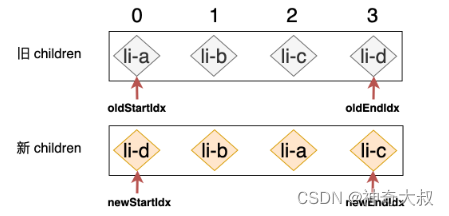
- 使用四个变量 oldStartIdx、oldEndIdx、newStartIdx 以及 newEndIdx 分别存储旧 children 和新 children 的两个端点的位置索引
let oldStartIdx = 0
let oldEndIdx = prevChildren.length - 1
let newStartIdx = 0
let newEndIdx = nextChildren.length - 1- 除了位置索引之外,还需要拿到四个位置索引所指向的 VNode
let oldStartVNode = prevChildren[oldStartIdx]
let oldEndVNode = prevChildren[oldEndIdx]
let newStartVNode = nextChildren[newStartIdx]
let newEndVNode = nextChildren[newEndIdx]比较策略
- 使用旧 children 的头一个 VNode 与新 children 的头一个 VNode 比对,即 oldStartVNode 和 newStartVNode 比较对。
- 使用旧 children 的最后一个 VNode 与新 children 的最后一个 VNode 比对,即 oldEndVNode 和 newEndVNode 比对。
- 使用旧 children 的头一个 VNode 与新 children 的最后一个 VNode 比对,即 oldStartVNode 和 newEndVNode 比对。
- 使用旧 children 的最后一个 VNode 与新 children 的头一个 VNode 比对,即 oldEndVNode 和 newStartVNode 比对。
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比对} else if (oldEndVNode.key === newEndVNode.key) {// 步骤二:oldEndVNode 和 newEndVNode 比对} else if (oldStartVNode.key === newEndVNode.key) {// 步骤三:oldStartVNode 和 newEndVNode 比对} else if (oldEndVNode.key === newStartVNode.key) {// 步骤四:oldEndVNode 和 newStartVNode 比对}
}
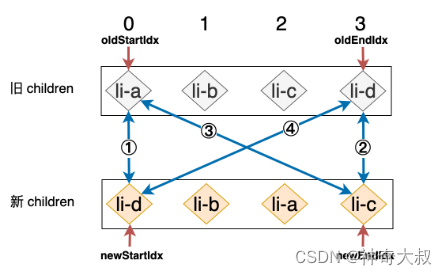
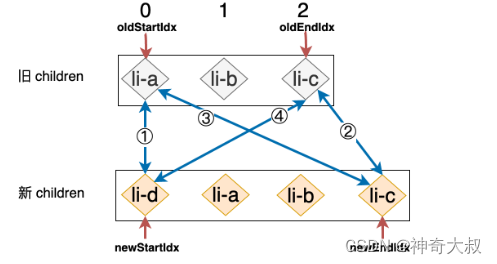
命中策略四
- 第一步:拿旧 children 中的 li-a 和新 children 中的 li-d 进行比对,由于二者 key 值不同,所以不可复用,什么都不做。
- 第二步:拿旧 children 中的 li-d 和新 children 中的 li-c 进行比对,同样不可复用,什么都不做。
- 第三步:拿旧 children 中的 li-a 和新 children 中的 li-c 进行比对,什么都不做。
- 第四步:拿旧 children 中的 li-d 和新 children 中的 li-d 进行比对,由于这两个节点拥有相同的 key 值,所以我们在这次比对的过程中找到了可复用的节点。
- li-d 节点所对应的真实 DOM 原本是最后一个子节点,并且更新之后它应该变成第一个子节点。所以我们需要把 li-d 所对应的真实 DOM 移动到最前方即可:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比对} else if (oldEndVNode.key === newEndVNode.key) {// 步骤二:oldEndVNode 和 newEndVNode 比对} else if (oldStartVNode.key === newEndVNode.key) {// 步骤三:oldStartVNode 和 newEndVNode 比对} else if (oldEndVNode.key === newStartVNode.key) {// 步骤四:oldEndVNode 和 newStartVNode 比对// 先调用 patch 函数完成更新patch(oldEndVNode, newStartVNode, container)// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点container.insertBefore(oldEndVNode.el, oldStartVNode.el)// 更新索引,指向下一个位置oldEndVNode = prevChildren[--oldEndIdx]newStartVNode = nextChildren[++newStartIdx]}
}命中策略二
- 上一步更新完成之后,新的索引关系可以用下图来表示:
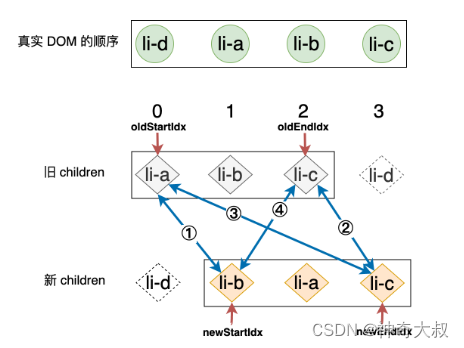
- 第一步:拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对,由于二者 key 值不同,所以不可复用,什么都不做。
- 第二步:拿旧 children 中的 li-c 和新 children 中的 li-c 进行比对,此时,由于二者拥有相同的 key,所以是可复用的节点,但是由于二者在新旧 children 中都是最末尾的一个节点,所以是不需要进行移动操作的,只需要调用 patch 函数更新即可,同时将相应的索引前移一位
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比对} else if (oldEndVNode.key === newEndVNode.key) {// 步骤二:oldEndVNode 和 newEndVNode 比对// 调用 patch 函数更新patch(oldEndVNode, newEndVNode, container)// 更新索引,指向下一个位置oldEndVNode = prevChildren[--oldEndIdx]newEndVNode = nextChildren[--newEndIdx]} else if (oldStartVNode.key === newEndVNode.key) {// 步骤三:oldStartVNode 和 newEndVNode 比对} else if (oldEndVNode.key === newStartVNode.key) {// 步骤四:oldEndVNode 和 newStartVNode 比对// 先调用 patch 函数完成更新patch(oldEndVNode, newStartVNode, container)// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点container.insertBefore(oldEndVNode.el, oldStartVNode.el)// 更新索引,指向下一个位置oldEndVNode = prevChildren[--oldEndIdx]newStartVNode = nextChildren[++newStartIdx]}
}命中策略三
- 上一步更新完成之后,新的索引关系可以用下图来表示:
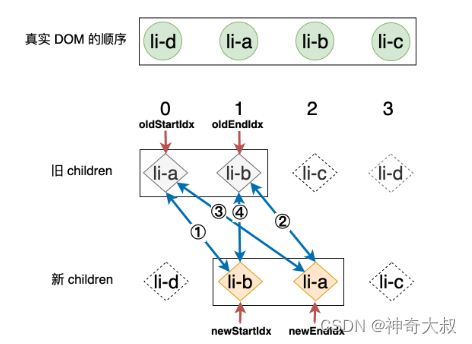
- 第一步:拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对,由于二者 key 值不同,所以不可复用,什么都不做。
- 第二步:拿旧 children 中的 li-b 和新 children 中的 li-a 进行比对,不可复用,什么都不做。
- 第三步:拿旧 children 中的 li-a 和新 children 中的 li-a 进行比对,此时,我们找到了可复用的节点。
- 这一次满足的条件是:oldStartVNode.key === newEndVNode.key,这说明:li-a 节点所对应的真实 DOM 原本是第一个子节点,但现在变成了“最后”一个子节点,这里的“最后”并不是指真正意义上的最后一个节点,而是指当前索引范围内的最后一个节点。所以移动操作也是比较明显的,我们将 oldStartVNode 对应的真实 DOM 移动到 oldEndVNode 所对应真实 DOM 的后面即可
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比对} else if (oldEndVNode.key === newEndVNode.key) {// 步骤二:oldEndVNode 和 newEndVNode 比对// 调用 patch 函数更新patch(oldEndVNode, newEndVNode, container)// 更新索引,指向下一个位置oldEndVNode = prevChildren[--oldEndIdx]newEndVNode = newEndVNode[--newEndIdx]} else if (oldStartVNode.key === newEndVNode.key) {// 步骤三:oldStartVNode 和 newEndVNode 比对// 调用 patch 函数更新patch(oldStartVNode, newEndVNode, container)// 将 oldStartVNode.el 移动到 oldEndVNode.el 的后面,也就是 oldEndVNode.el.nextSibling 的前面container.insertBefore(oldStartVNode.el,oldEndVNode.el.nextSibling)// 更新索引,指向下一个位置oldStartVNode = prevChildren[++oldStartIdx]newEndVNode = nextChildren[--newEndIdx]} else if (oldEndVNode.key === newStartVNode.key) {// 步骤四:oldEndVNode 和 newStartVNode 比对// 先调用 patch 函数完成更新patch(oldEndVNode, newStartVNode, container)// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点container.insertBefore(oldEndVNode.el, oldStartVNode.el)// 更新索引,指向下一个位置oldEndVNode = prevChildren[--oldEndIdx]newStartVNode = nextChildren[++newStartIdx]}
}命中策略一
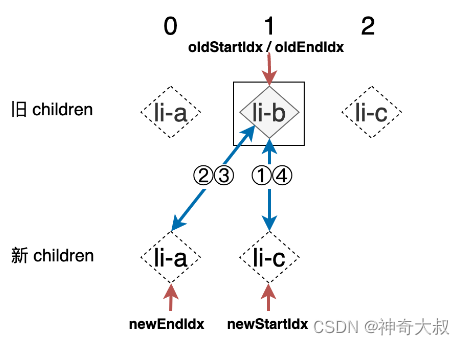
- 上一步更新完成之后,新的索引关系可以用下图来表示:
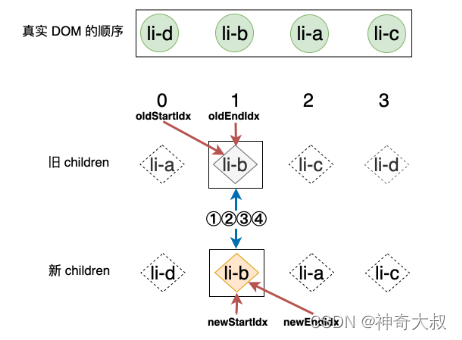
- 第一步:拿旧 children 中的 li-b 和新 children 中的 li-b 进行比对,二者拥有相同的 key,可复用
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比对// 调用 patch 函数更新patch(oldStartVNode, newStartVNode, container)// 更新索引,指向下一个位置oldStartVNode = prevChildren[++oldStartIdx]newStartVNode = nextChildren[++newStartIdx]} else if (oldEndVNode.key === newEndVNode.key) {// 省略...} else if (oldStartVNode.key === newEndVNode.key) {// 省略...} else if (oldEndVNode.key === newStartVNode.key) {// 省略...}
}未命中四种策略,遍历旧节点列表
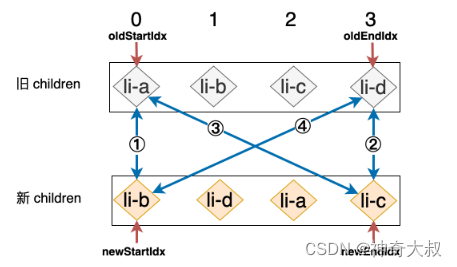
- 上图中 ①、②、③、④ 这四步中的每一步比对,都无法找到可复用的节点
- 策略为:拿新 children 中的第一个节点尝试去旧 children 中寻找,试图找到拥有相同 key 值的节点
- 如果在旧的 children 中找到了与新 children 中第一个节点拥有相同 key 值的节点,这意味着:旧 children 中的这个节点所对应的真实 DOM 在新 children 的顺序中,已经变成了第一个节点。所以我们需要把该节点所对应的真实 DOM 移动到最前头
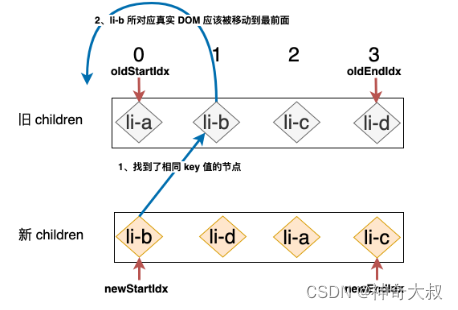
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (oldStartVNode.key === newStartVNode.key) {// 省略...} else if (oldEndVNode.key === newEndVNode.key) {// 省略...} else if (oldStartVNode.key === newEndVNode.key) {// 省略...} else if (oldEndVNode.key === newStartVNode.key) {// 省略...} else {// 遍历旧 children,试图寻找与 newStartVNode 拥有相同 key 值的元素const idxInOld = prevChildren.findIndex(node => node.key === newStartVNode.key)if (idxInOld >= 0) {// vnodeToMove 就是在旧 children 中找到的节点,该节点所对应的真实 DOM 应该被移动到最前面const vnodeToMove = prevChildren[idxInOld]// 调用 patch 函数完成更新patch(vnodeToMove, newStartVNode, container)// 把 vnodeToMove.el 移动到最前面,即 oldStartVNode.el 的前面container.insertBefore(vnodeToMove.el, oldStartVNode.el)// 由于旧 children 中该位置的节点所对应的真实 DOM 已经被移动,所以将其设置为 undefinedprevChildren[idxInOld] = undefined}// 将 newStartIdx 下移一位newStartVNode = nextChildren[++newStartIdx]}
}- 因为旧节点已经找到并处理过了,所以后续的双端比较需要跳过处理过的节点
- 将旧 children 中的 li-b 节点变成 undefined,然后旧节点指针遇到时跳过
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {// undefined 跳过if (!oldStartVNode) {oldStartVNode = prevChildren[++oldStartIdx]} else if (!oldEndVNode) { // undefined 跳过oldEndVNode = prevChildren[--oldEndIdx]} else if (oldStartVNode.key === newStartVNode.key) {// 省略...} else if (oldEndVNode.key === newEndVNode.key) {// 省略...} else if (oldStartVNode.key === newEndVNode.key) {// 省略...} else if (oldEndVNode.key === newStartVNode.key) {// 省略...} else {const idxInOld = prevChildren.findIndex(node => node.key === newStartVNode.key)if (idxInOld >= 0) {const vnodeToMove = prevChildren[idxInOld]patch(vnodeToMove, newStartVNode, container)prevChildren[idxInOld] = undefinedcontainer.insertBefore(vnodeToMove.el, oldStartVNode.el)}newStartVNode = nextChildren[++newStartIdx]}
}新增情况一
- 节点所在的双端不满足四种策略,也不满足能找到旧节点
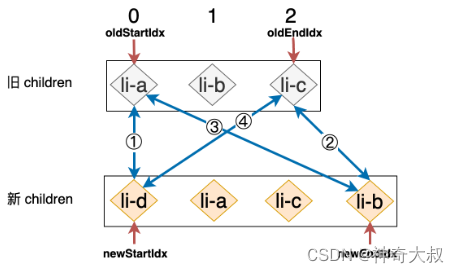
- 在新 children 中,节点 li-d 是一个全新的节点。在这个例子中 ①、②、③、④ 这四步的比对仍然无法找到可复用节点,所以我们会尝试拿着新 children 中的 li-d 节点去旧的 children 寻找与之拥有相同 key 值的节点,结果很显然,我们无法找到这样的节点。这时说明该节点是一个全新的节点,我们应该将其挂载到容器中,由于 li-d 节点的位置索引是 newStartIdx,这说明 li-d 节点是当前这一轮比较中的“第一个”节点,所以只要把它挂载到位于 oldStartIdx 位置的节点所对应的真实 DOM 前面就可以了,即 oldStartVNode.el
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {if (!oldStartVNode) {oldStartVNode = prevChildren[++oldStartIdx]} else if (!oldEndVNode) {oldEndVNode = prevChildren[--oldEndIdx]} else if (oldStartVNode.key === newStartVNode.key) {// 省略...} else if (oldEndVNode.key === newEndVNode.key) {// 省略...} else if (oldStartVNode.key === newEndVNode.key) {// 省略...} else if (oldEndVNode.key === newStartVNode.key) {// 省略...} else {const idxInOld = prevChildren.findIndex(node => node.key === newStartVNode.key)if (idxInOld >= 0) {const vnodeToMove = prevChildren[idxInOld]patch(vnodeToMove, newStartVNode, container)prevChildren[idxInOld] = undefinedcontainer.insertBefore(vnodeToMove.el, oldStartVNode.el)} else {// 使用 mount 函数挂载新节点,如果传入了最后一个参数,内部也是使用 insertBeforemount(newStartVNode, container, false, oldStartVNode.el)}newStartVNode = nextChildren[++newStartIdx]}
}新增情况二
- 节点所在的双端优先满足了四种策略
- 最终双端比较完成后结果
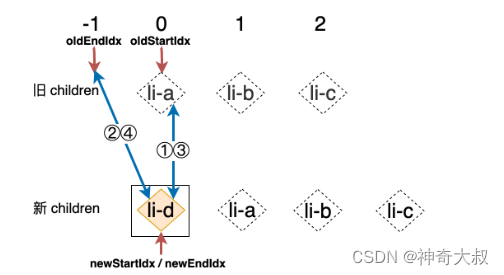
- oldEndIdx 将比 oldStartIdx 的值要小,对 oldEndIdx 和 oldStartIdx 的值进行检查,如果在循环结束之后 oldEndIdx 的值小于 oldStartIdx 的值则说明新的 children 中存在还没有被处理的全新节点,这时我们应该调用 mount 函数将其挂载到容器元素中,观察上图可知,我们只需要把这些全新的节点添加到 oldStartIdx 索引所指向的节点之前即可
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {// 省略...
}
if (oldEndIdx < oldStartIdx) {// 添加新节点for (let i = newStartIdx; i <= newEndIdx; i++) {mount(nextChildren[i], container, false, oldStartVNode.el)}
}删除节点
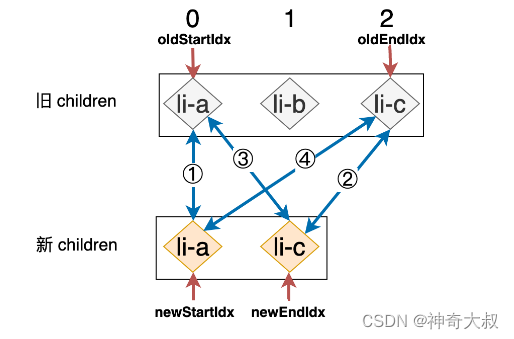
- 在进行双端比较后
- 此时 newEndIdx 的值小于 newStartIdx 的值,所以循环将终止,但是通过上图可以发现,旧 children 中的 li-b 节点没有得到被处理的机会,我们应该将其移除才行,循环结束后,一旦满足条件 newEndIdx < newStartId 则说明有元素需要被移除
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {// 省略...
}
if (oldEndIdx < oldStartIdx) {// 添加新节点for (let i = newStartIdx; i <= newEndIdx; i++) {mount(nextChildren[i], container, false, oldStartVNode.el)}
} else if (newEndIdx < newStartIdx) {// 移除操作for (let i = oldStartIdx; i <= oldEndIdx; i++) {container.removeChild(prevChildren[i].el)}
}双端比较的优势
- 对于如下节点情况
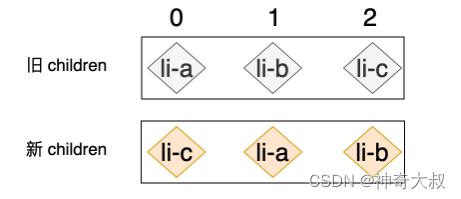
- 如果采用 React 根据相对位置的diff 方式来对上例进行更新,则会执行两次移动操作
- 首先会把 li-a 节点对应的真实 DOM 移动到 li-c 节点对应的真实 DOM 的后面
- 接着再把 li-b 节点所对应的真实 DOM 移动到 li-a 节点所对应真实 DOM 的后面,即:
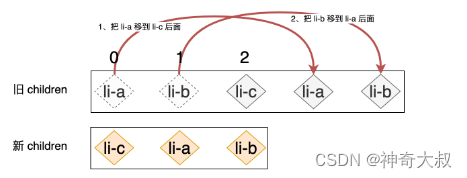
- 如果采用 vue 的双端比较 diff
- 第一步:拿旧 children 中的 li-a 和新 children 中的 li-c 进行比对,由于二者 key 值不同,所以不可复用,什么都不做。
- 第二步:拿旧 children 中的 li-c 和新 children 中的 li-b 进行比对,不可复用,什么都不做。
- 第三步:拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对,不可复用,什么都不做。
- 第四步:拿旧 children 中的 li-c 和新 children 中的 li-c 进行比对,此时,两个节点拥有相同的 key 值,可复用。
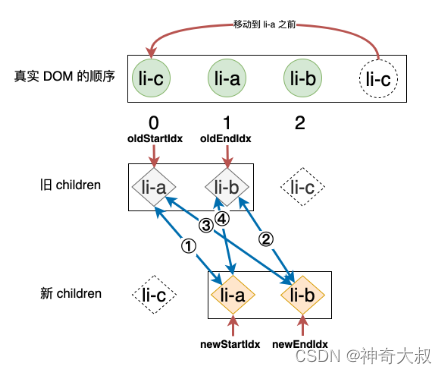
- 可以看到,我们只通过一次 DOM 移动,就使得真实 DOM 的顺序与新 children 中节点的顺序一致,后序只需要 patch 不需要移动。双端比较更加符合人类思维,在移动 DOM 方面更具有普适性,能减少因为 DOM 结构的差异而产生的影响
相关文章:

vue diff 双端比较算法
文章目录 双端指针比较策略命中策略四命中策略二命中策略三命中策略一未命中四种策略,遍历旧节点列表新增情况一新增情况二 删除节点双端比较的优势 双端指针 使用四个变量 oldStartIdx、oldEndIdx、newStartIdx 以及 newEndIdx 分别存储旧 children 和新 children …...
)
初识React: 基础(概念 特点 高效原因 虚拟DOM JSX语法 组件)
1.什么是React? React是一个由Facebook开源的JavaScript库,它主要用于构建用户界面。React的特点是使用组件化的思想来构建界面,使得代码的可复用性和可维护性大大提高。React还引入了虚拟DOM的概念,减少了对真实DOM的直接操作,…...

自监督去噪:Neighbor2Neighbor原理分析与总结
文章目录 1. 方法原理1.1 先前方法总结1.2 Noise2Noise回顾1.3 从Noise2Noise到Neighbor2Neighbor1.4 框架结构2. 实验结果3. 总结 文章链接:https://arxiv.org/abs/2101.02824 参考博客:https://arxiv.org/abs/2101.02824 1. 方法原理 1.1 先前方法总…...
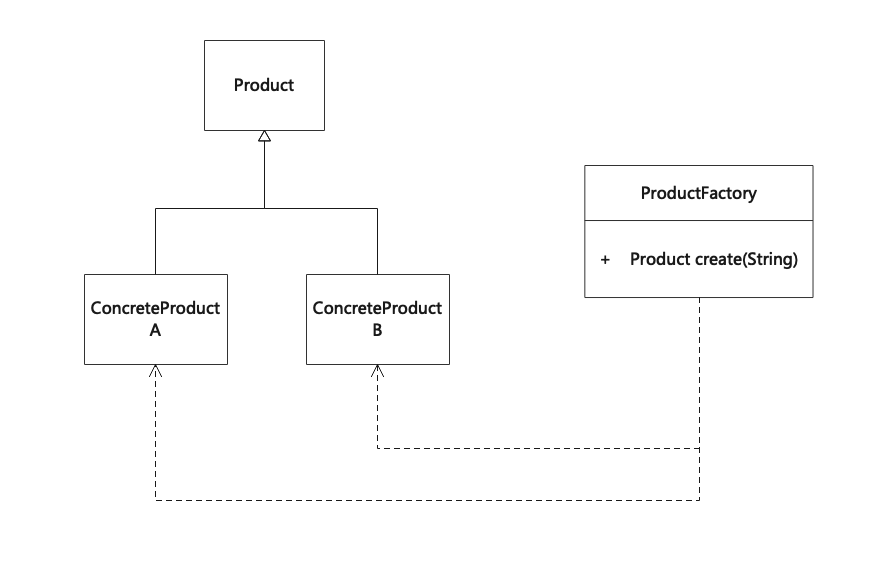
简单工厂模式(Simple Factory)
简单工厂模式,又称为静态工厂方法(Static Factory Method)模式。在简单工厂模式中,可以根据参数的不同返回不同类的实例。简单工厂模式专门定义一个类来负责创建其他类的实例,被创建的实例通常都具有共同的父类。简单工厂模式不属于GoF的23个…...

Agent:OpenAI的下一步,亚马逊云科技站在第5层
什么是Agent?在大模型语境下,可以理解成能自主理解、规划、执行复杂任务的系统。Agent也将成为新的起点,成为各行各业构建新一代AI应用必不可少的组成部分。 对此,初创公司Seednapse AI创始人提出构建AI应用的五层基石理论&#…...
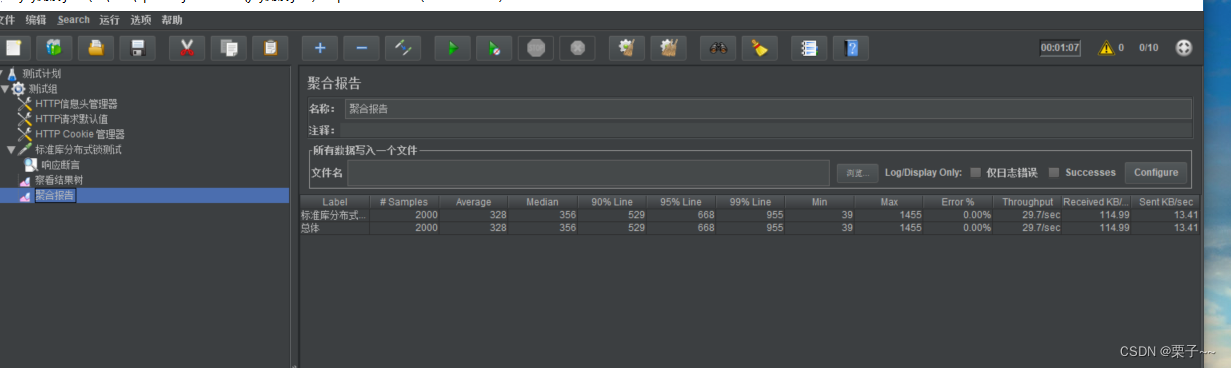
JMeter 4.x 简单使用
文章目录 前言JMeter 4.x 简单使用1. 启动2. 设置成中文3. 接口测试3.1. 设置线程组3.2. HTTP信息请求头管理器3.3. 添加HTTP请求默认值3.4. 添加HTTP cookie 管理3.5. 添加http请求3.5.1. 添加断言 3.6. 添加监听器-查看结果树3.7. 添加监听器-聚合报告 4. 测试 前言 如果您觉…...

深入NLTK:Python自然语言处理库高级教程
在前面的初级和中级教程中,我们了解了NLTK库中的基本和进阶功能,如词干提取、词形还原、n-gram模型和词云的绘制等。在本篇高级教程中,我们将深入探索NLTK的更多高级功能,包括句法解析、命名实体识别、情感分析以及文本分类。 一…...

React 用来解析html 标签的方法
在React中,解析HTML标签通常是使用JSX(JavaScript XML)语法的一部分。JSX允许您在JavaScript代码中编写类似HTML的标记,然后通过React进行解析和渲染。 以下是React中解析HTML标签的几种常见方式: 直接在JSX中使用标…...
【C++】做一个飞机空战小游戏(五)——getch()控制两个飞机图标移动(控制光标位置)
[导读]本系列博文内容链接如下: 【C】做一个飞机空战小游戏(一)——使用getch()函数获得键盘码值 【C】做一个飞机空战小游戏(二)——利用getch()函数实现键盘控制单个字符移动【C】做一个飞机空战小游戏(三)——getch()函数控制任意造型飞机图标移动 【C】做一个飞…...
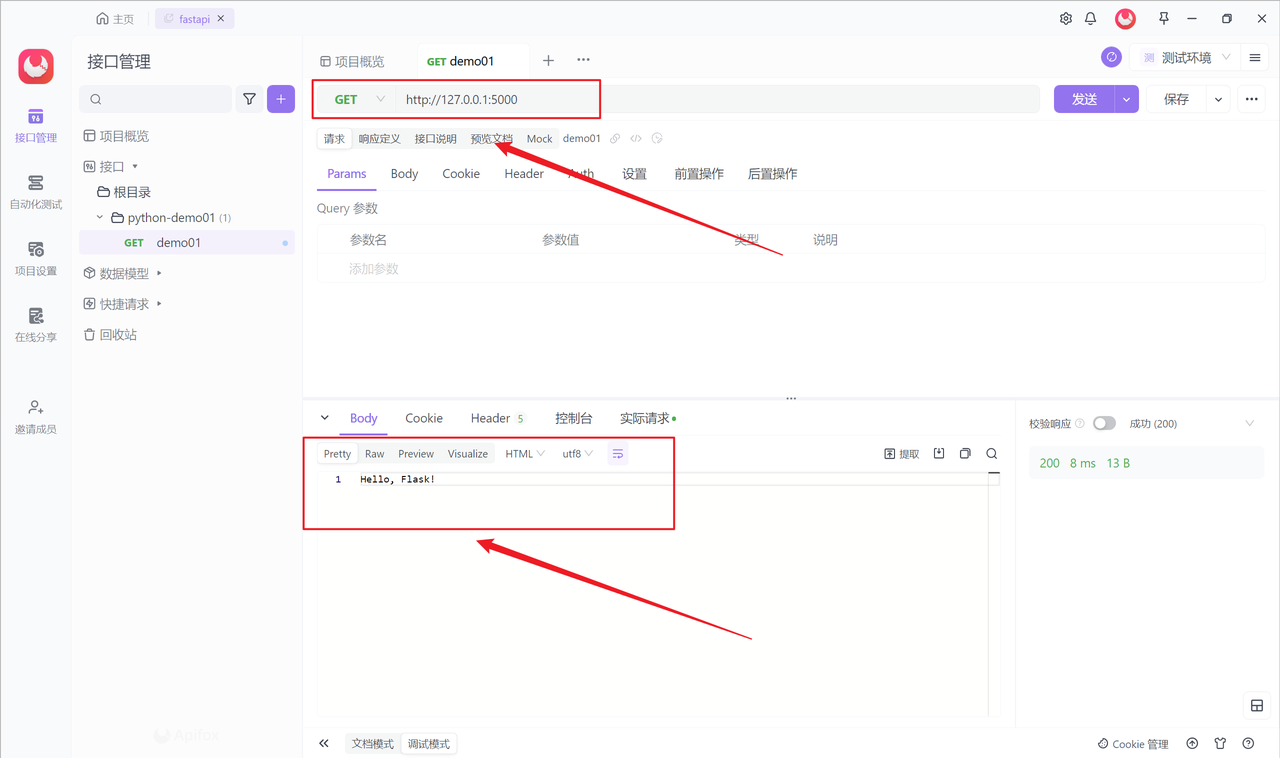
Flask 是什么?Flask框架详解及实践指南
Flask 是一个轻量级的 Python Web 框架,它被广泛用于构建 Web 应用程序和 API。Flask 简单易用,具有灵活性和可扩展性,是许多开发者喜欢用其构建项目的原因。本文将介绍 Flask 是什么以及如何使用它来构建 Web 应用程序,同时提供一…...
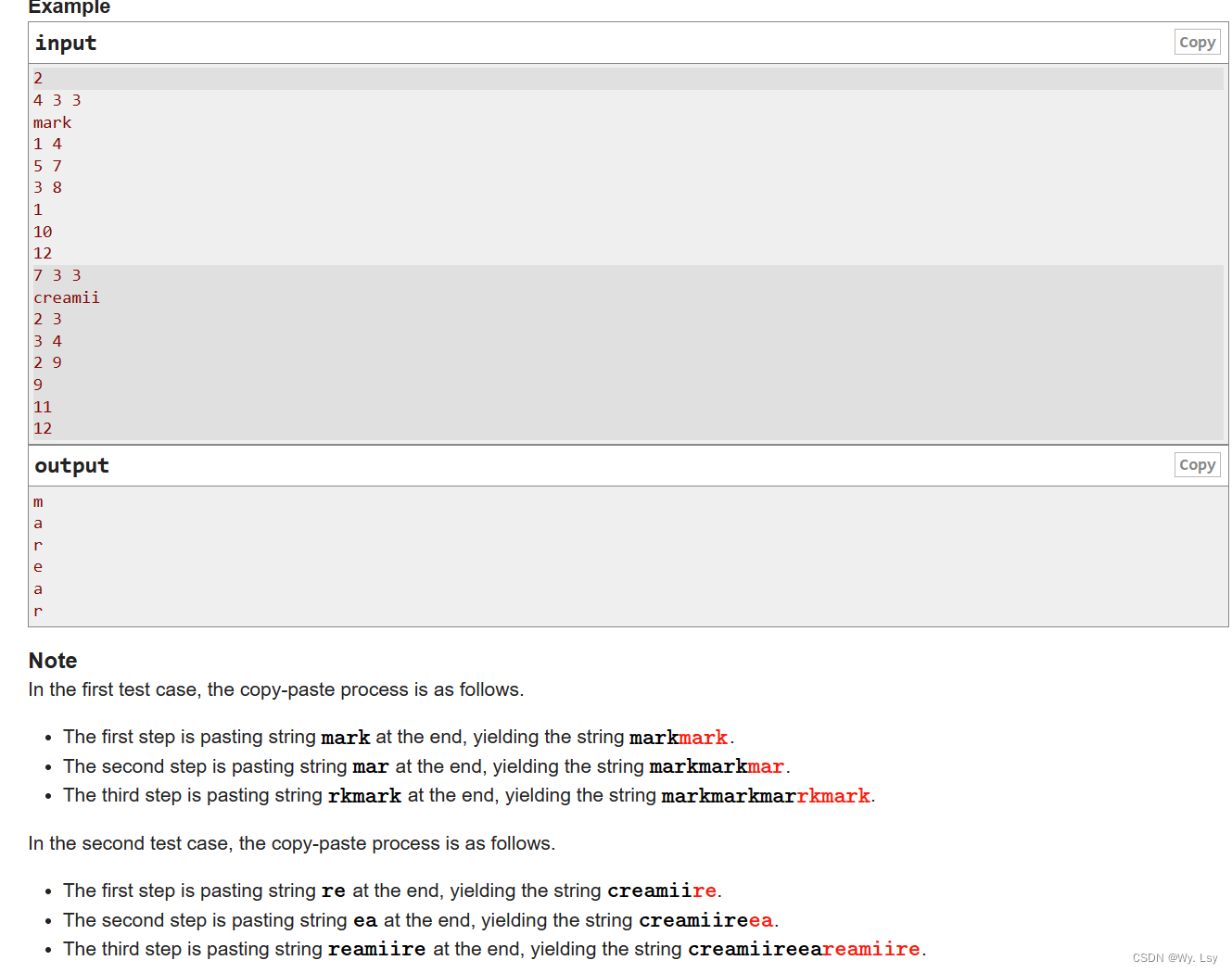
C. Mark and His Unfinished Essay - 思维
分析: 直接模拟操作会mle,可以每次复制记录对应源字符串的下标,可以记录每次字符串增加的长度的左右端点下标,可以发现左端点与读入的l是对应的,因此就可以向前移到l的位置,这样层层递归,就能找…...

Java的变量与常量
目录 变量 声明变量 变量的声明类型 变量的声明方式:变量名 变量名的标识符 初始化变量 常量 关键字final 类常量 总结 变量和常量都是用来存储值和数据的基本数据类型存储方式,但二者之间有一些关键差别。 变量 在Java中,每个变…...
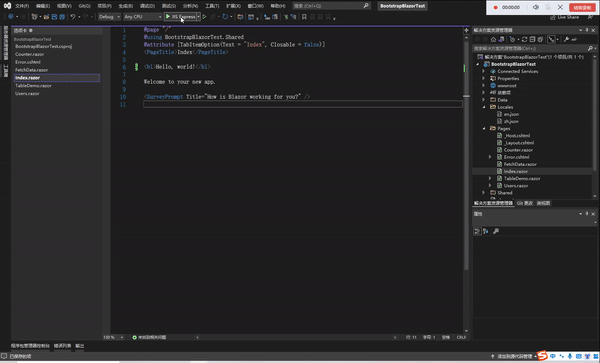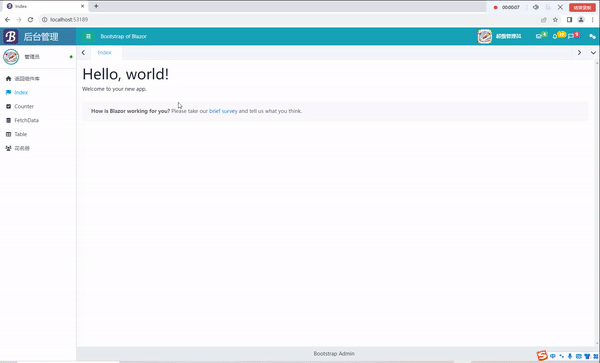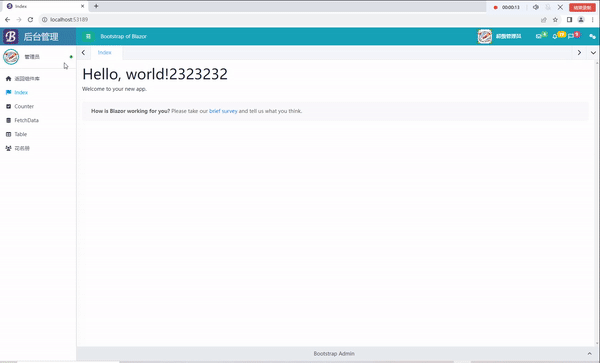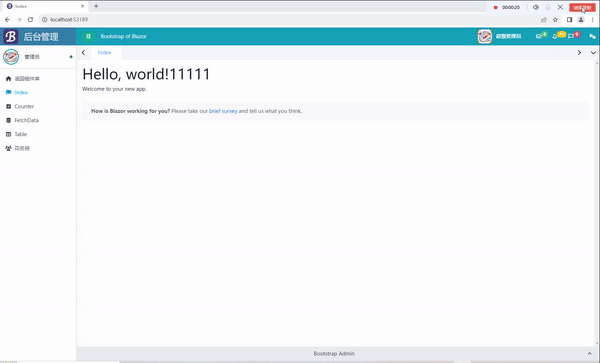
C# Blazor 学习笔记(6):热重置问题解决
文章目录 前言热重置问题描述解决方法演示 总结 前言 我最近在使用Blazor的时候,使用了BootstrapBlazor(以下简称BB)创建模板的时候,发现热重置无效。经过了一上午的折腾,我终于解决了这个问题。 热重置 问题描述 …...

一百四十六、Xmanager——Xmanager5连接Xshell7并控制服务器桌面
一、目的 由于kettle安装在Linux上,Xshell启动后需要Xmanager。而Xmanager7版本受限、没有免费版,所以就用Xmanager5去连接Xshell7 二、Xmanager5安装包来源 (一)注册码 注册码:101210-450789-147200 (…...

用Rust实现23种设计模式之 模板方法模式
关注我,学习Rust不迷路!! 模板方法模式是一种行为型设计模式,它定义了一个算法的骨架,将一些步骤的实现延迟到子类中。以下是模板方法模式的优点和使用场景: 优点: 提高代码复用性࿱…...
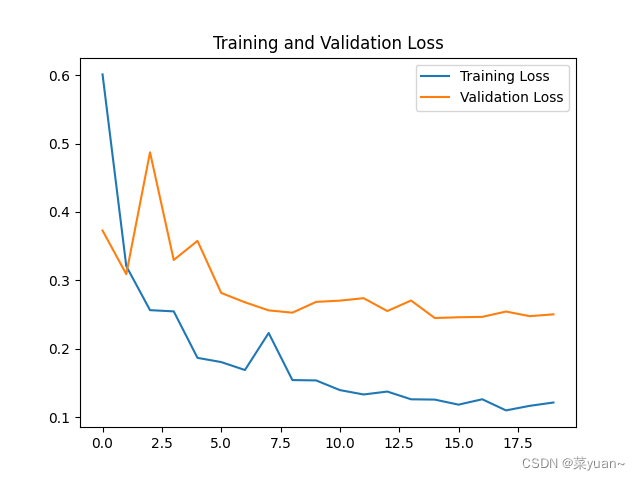
python与深度学习(十三):CNN和IKUN模型
目录 1. 说明2. IKUN模型2.1 导入相关库2.2 建立模型2.3 模型编译2.4 数据生成器2.5 模型训练2.6 模型保存2.7 模型训练结果的可视化 3. IKUN的CNN模型可视化结果图4. 完整代码 1. 说明 本篇文章是CNN的另外一个例子,IKUN模型,是自制数据集的例子。之前…...

题目:2283.判断一个数的数字计数是否等于数位的值
题目来源: leetcode题目,网址:2283. 判断一个数的数字计数是否等于数位的值 - 力扣(LeetCode) 解题思路: 两次遍历。第一次对字符串中每个出现的数字计数。第二次比较数字计数与数位的值是否相等。 解…...

任务14、无缝衔接,MidJourney瓷砖(Tile)参数制作精良贴图
14.1 任务概述 在这个实验任务中,我们将深入探索《Midjourney Ai绘画》中的Tile技术和其在艺术创作中的具有挑战性的应用。此任务将通过理论学习与实践操作相结合的方式,让参与者更好地理解Tile的核心概念,熟练掌握如何在Midjourney平台上使用Tile参数,并实际运用到AI绘画…...

【uniapp APP如何优化】
以下是一些可以进行优化的建议: 1. 减少网络请求次数:尽量避免在首页加载时请求大量数据,可以考虑使用分页加载,或者使用下拉刷新和上拉加载更多的方式。 2. 减小图片大小:使用压缩图片的工具,可以尽可能…...
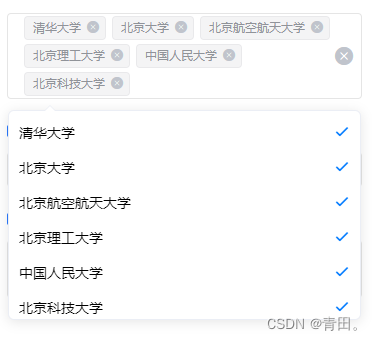
uni-app——下拉框多选
一、组件components/my-selectCheckbox.vue <template><view class"uni-stat__select"><span v-if"label" class"uni-label-text">{{label :}}</span><view class"uni-stat-box" :class"…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
