论文《Contrastive Meta Learning with Behavior Multiplicity for Recommendation》阅读
论文《Contrastive Meta Learning with Behavior Multiplicity for Recommendation》阅读
- 论文概况
- 论文主要贡献
- Background & Motivation
- 方法论
- 单行为图神经网络(Behavior-aware GNN)
- 多行为对比学习
- 元对比编码
- 模型训练
- 实验部分
- 论文总结
论文概况
今天带来的是发表在WSDM 2022上关于多行为推荐的对比元学习论文《Contrastive Meta Learning with Behavior Multiplicity for Recommendation》,提出模型CML。论文由香港大学韦玮等人完成。
论文地址:Paper
代码地址:Code
论文主要贡献
本文的主要贡献是提出了一个多行为推荐(Multi-Behavior Recommendation)框架CML (Contrastive Meta Learning),主要通过元学习(Meta Learning)结合对比学习(Contrastive Learning)完成,主要创新在于对比学习与元学习框架的结合。
Background & Motivation
论文的intro部分主要介绍了多行为推荐的必要性,即能够完成多行为之间的关联的学习。
之后引出主要问题,即多行为推荐中目标行为(target behavior)比较稀疏,由此引出自监督学习的必要性。
(自监督学习解决多行为推荐的作品之前应该就已经有解决,本文的主要创新在于meta learning,但是intro部分并没有给出meta框架的必要性)
方法论

如上框架图所示,模型CML主要由图神经网络和多行为对比学习框架结合完成,并通过元学习进行模型参数的学习。
单行为图神经网络(Behavior-aware GNN)
e u k , ( l + 1 ) = ∑ i ∈ N u k e i k , ( l ) (1) \mathbf{e}_{u}^{k,(l+1)}=\sum_{i \in \mathcal{N}_{u}^{k}} \mathbf{e}_{i}^{k,(l)} \tag{1} euk,(l+1)=i∈Nuk∑eik,(l)(1)
e i k , ( l + 1 ) = ∑ u ∈ N i k e u k , ( l ) (2) \mathbf{e}_{i}^{k,(l+1)}=\sum_{u \in \mathcal{N}_{i}^{k}} \mathbf{e}_{u}^{k,(l)} \tag{2} eik,(l+1)=u∈Nik∑euk,(l)(2)
其中 k ∈ { 1 , 2 , ⋯ , K } k \in \{1, 2, \cdots, K\} k∈{1,2,⋯,K}用于标记行为编号, l ∈ { 1 , 2 , ⋯ , L } l \in \{1,2,\cdots, L\} l∈{1,2,⋯,L}用于标记层深, u ∈ U u\in \mathcal{U} u∈U 及 i ∈ I i \in \mathcal{I} i∈I 分别表示任意用户及物品。图神经网络采用LightGCN的轻量化聚合方案。
多行为聚合采用一个均值池化外加单层MLP完成,激活函数使用 P R e L U ( ⋅ ) PReLU(\cdot) PReLU(⋅)函数完成,如下所示:
e u = PReLu ( W L ⋅ ∑ k ∈ K e u k , ( L + 1 ) K ) (3) \mathbf{e}_{u} = \operatorname{PReLu}\left(\mathbf{W}^{L} \cdot \frac{\sum_{k \in K} \mathbf{e}_{u}^{k,(L+1)}}{K}\right) \tag{3} eu=PReLu(WL⋅K∑k∈Keuk,(L+1))(3)
这里对公式(3)进行了小修改,原文应该是表述有点问题,作者应该是使用多层GNN最后一层的embedding进行最终表示,并且后文并没有交代,这里先这样表示,并与后文中符号 e u \mathbf{e}_{u} eu保持一致。
多行为对比学习
作者使用InfoNCE来突出对比对象,即同一用户的多个行为进行靠近(positive views),不同用户进行疏远(negative views),如下所示:
L c l k , k ′ = ∑ u ∈ U − log exp ( φ ( e u k , e u k ′ ) / τ ) ∑ u ′ ∈ U exp ( φ ( e u k , e u ′ k ′ ) / τ ) (4) \mathcal{L}_{c l}^{k, k^{\prime}}=\sum_{u \in \mathcal{U}}-\log \frac{\exp \left(\varphi\left(\mathbf{e}_{u}^{k}, \mathbf{e}_{u}^{k^{\prime}}\right) / \tau\right)}{\sum_{u^{\prime} \in \mathcal{U}} \exp \left(\varphi\left(\mathbf{e}_{u}^{k}, \mathbf{e}_{u^{\prime}}^{k^{\prime}}\right) / \tau\right)} \tag{4} Lclk,k′=u∈U∑−log∑u′∈Uexp(φ(euk,eu′k′)/τ)exp(φ(euk,euk′)/τ)(4)
私以为,这里的下标 u ∈ U u \in \mathcal{U} u∈U 换成 v ∈ U ∪ I v \in \mathcal{U} \cup \mathcal{I} v∈U∪I 更为合适。公式(4)中, φ ( ⋅ ) \varphi\left( \cdot \right) φ(⋅) 是判别函数,但是文中并没有进行进一步说明如何实现,是cosine还是内积还是什么。 τ \tau τ 是温度系数,文中也没有进行说明赋值到底多少。
针对目标行为标号 k k k及辅助行为标号 k ′ ∈ { 1 , 2 , ⋯ , K } k^{\prime} \in \{1, 2, \cdots, K\} k′∈{1,2,⋯,K},共形成 K K K 对 对比学习目标损失项,合在一起构成总的对比学习损失项:
L c l = L c l k , 1 + … + L c l k , k ′ + … + L c l k , K (5) \mathcal{L}_{c l}=\mathcal{L}_{c l}^{k, 1}+\ldots+\mathcal{L}_{c l}^{k, k^{\prime}}+\ldots+\mathcal{L}_{c l}^{k, K} \tag{5} Lcl=Lclk,1+…+Lclk,k′+…+Lclk,K(5)
元对比编码
Z u , 1 k , k ′ = ( d ( L c l k , k ′ ) ⋅ γ ) ∥ e u k ′ ∥ e u (6) \mathbf{Z}_{u, 1}^{k, k^{\prime}}=\left(d\left(\mathcal{L}_{c l}^{k, k^{\prime}}\right) \cdot \gamma\right)\left\|\mathbf{e}_{u}^{k^{\prime}}\right\| \mathbf{e}_{u} \tag{6} Zu,1k,k′=(d(Lclk,k′)⋅γ) euk′ eu(6)
Z u , 2 k , k ′ = L c l k , k ′ ⋅ ( e u k ′ ∥ e u ) (7) \mathbf{Z}_{u, 2}^{k, k^{\prime}}=\mathcal{L}_{c l}^{k, k^{\prime}} \cdot\left(\mathbf{e}_{u}^{k^{\prime}} \| \mathbf{e}_{u}\right) \tag{7} Zu,2k,k′=Lclk,k′⋅(euk′∥eu)(7)
文中选择了两种encoder,一种直接进行乘法(公式(7)),一种进行了编码、放大和连接(公式(6))。编码函数 d ( ⋅ ) d\left( \cdot \right) d(⋅)(文中成为复制函数,这里还不甚了解,后续这一部分将进行扩充,同时需要指出的是作者并没有对函数 d ( ⋅ ) d(\cdot) d(⋅) 进行说明)。
ξ ( Z u k , k ′ ) = PReLU ( Z u k , k ′ ⋅ W ξ + b ξ ) (8) \xi\left(\mathbf{Z}_{u}^{k, k^{\prime}}\right)=\operatorname{PReLU}\left(\mathbf{Z}_{u}^{k, k^{\prime}} \cdot \mathbf{W}_{\xi}+\mathbf{b}_{\xi}\right) \tag{8} ξ(Zuk,k′)=PReLU(Zuk,k′⋅Wξ+bξ)(8)
ω u k , k ′ = ω u , 1 k , k ′ + ω u , 2 k , k ′ = ξ ( Z u , 1 k , k ′ ) + ξ ( Z u , 2 k , k ′ ) (9) \omega_{u}^{k, k^{\prime}}=\omega_{u, 1}^{k, k^{\prime}}+\omega_{u, 2}^{k, k^{\prime}}=\xi\left(\mathbf{Z}_{u, 1}^{k, k^{\prime}}\right)+\xi\left(\mathbf{Z}_{u, 2}^{k, k^{\prime}}\right) \tag{9} ωuk,k′=ωu,1k,k′+ωu,2k,k′=ξ(Zu,1k,k′)+ξ(Zu,2k,k′)(9)
同样使用单层MLP完成,这里的目的是将 Z u , ⋅ k , k ′ \mathbf{Z}_{u, \cdot}^{k, k^{\prime}} Zu,⋅k,k′变成标量,并融入到对比学习的各项loss中。
这里需要指出的是,文中对这里的解释是有问题的,一方面 PReLU ( ⋅ ) \operatorname{PReLU}\left( \cdot \right) PReLU(⋅) 输出的是向量,不是标量,与公式(9)相矛盾,另一方面,文中给出的维度也有问题( W ξ ∈ R d × d and b ξ ∈ R d \mathbf{W}_{\xi} \in \mathbb{R}^{d \times d} \text { and } \mathbf{b}_{\xi} \in \mathbb{R}^{d} Wξ∈Rd×d and bξ∈Rd 这里很明显是有问题的,两种encoder向量维度不同)。
模型训练
L B P R k = ∑ ( u , i + , i − ) ∈ O k − In ( sigmoid ( x ^ u , i + k − x ^ u , i − k ) ) + λ ∥ Θ ∥ 2 (10) \mathcal{L}_{B P R}^{k}=\sum_{\left(u, i^{+}, i^{-}\right) \in O_{k}}-\operatorname{In}\left(\operatorname{sigmoid}\left(\hat{x}_{u, i^{+}}^{k}-\hat{x}_{u, i^{-}}^{k}\right)\right)+\lambda\|\Theta\|^{2} \tag{10} LBPRk=(u,i+,i−)∈Ok∑−In(sigmoid(x^u,i+k−x^u,i−k))+λ∥Θ∥2(10)
L B P R k \mathcal{L}_{B P R}^{k} LBPRk表示目标行为 k k k 的BPR损失。
这个模型使用元学习框架进行参数更新,目前我对元学习部分的了解不是太深入,后续再进行补充。更新分为三步:1. 先优化图神经网络参数 Θ G \varTheta_{\mathcal{G}} ΘG;2. 根据优化过的 Θ G \varTheta_{\mathcal{G}} ΘG 对对比学习参数 Θ M \varTheta_{M} ΘM 进行优化;3. 根据优化完成的 Θ M \varTheta_{M} ΘM 进一步优化参数 Θ G \varTheta_{\mathcal{G}} ΘG。如下图所示。

元学习的宗旨就是学会学习(learn to learn),其大致思想是通过对数据集进行分割,分别完成对目标模型和目标模型的设置的学习。结合到本文的模型即为,分别学习模型的参数,以及模型关键参数的设置(即 ω u k , k ′ \omega_{u}^{k, k^{\prime}} ωuk,k′)。这里可能有理解不到位或者错误的地方,欢迎评论区指出。
最终,模型的损失函数可以定义为:
Θ G ∗ = arg min θ ≜ ∑ k = 1 K ∑ b = 1 B ( M ( ( L c l , k trainumeta , E , E k ) ; Θ M ) ⋅ L c l , k train + M ( ( L bpr , k train ∪ meta , E , E k ) ; Θ M ) ⋅ L b p r , k train ) (11) \begin{aligned} \Theta_{\mathcal{G}}^{*} &=\underset{\theta}{\arg \min } \triangleq \sum_{k=1}^{K} \sum_{b=1}^{B}\left(\mathcal{M}\left(\left(\mathcal{L}_{c l, k}^{\text {trainumeta }}, \mathbf{E}, \mathbf{E}^{k}\right) ; \Theta_{\mathcal{M}}\right) \cdot \mathcal{L}_{c l, k}^{\text {train }} \right. \\ & \left. + \mathcal{M}\left(\left(\mathcal{L}_{\text {bpr }, k}^{\text {train } \cup \text { meta }}, \mathbf{E}, \mathbf{E}^{k}\right) ; \Theta_{\mathcal{M}}\right) \cdot \mathcal{L}_{b p r, k}^{\text {train }}\right) \end{aligned} \tag{11} ΘG∗=θargmin≜k=1∑Kb=1∑B(M((Lcl,ktrainumeta ,E,Ek);ΘM)⋅Lcl,ktrain +M((Lbpr ,ktrain ∪ meta ,E,Ek);ΘM)⋅Lbpr,ktrain )(11)
结合到本例中,即为先进行模型的训练,再进行meta参数的学习。
实验部分
这里其余内容不再过多赘述,主要讲一下可视化部分,可视化部分(b)中,作者在上面显示了消融实验去掉对比学习部分的模型CML w/o CLF和总模型CML,分别展示在第一行和第二行中。为什么我看到的结果是CML w/o CLF要好于CML???这里着实不懂。

论文总结
本文提出了一种元对比学习框架CML,完成了多行为推荐任务。本文使用元学习结合对比学习是比较创新的,但文中也确实出现了一部分符号表示混乱,intro和related work不够全面等问题。另外,在参数设置部分,论文没有对参数进行具体说明,给复现带来了困难,具体来说,诸如 φ ( ⋅ , ⋅ ) \varphi(\cdot, \cdot) φ(⋅,⋅), τ \tau τ, d ( ⋅ ) d(\cdot) d(⋅), γ \gamma γ的参数设置值都没有进行说明。除此以外的其他部分完成得相当不错。欢迎大家在评论区进行批评指教。
相关文章:

论文《Contrastive Meta Learning with Behavior Multiplicity for Recommendation》阅读
论文《Contrastive Meta Learning with Behavior Multiplicity for Recommendation》阅读 论文概况论文主要贡献Background & Motivation方法论单行为图神经网络(Behavior-aware GNN)多行为对比学习元对比编码模型训练 实验部分论文总结 论文概况 今…...

K8S 部署 RocketMQ
文章目录 添加模板部署本地访问 集群使用 kubesphere 作为工具 添加模板 添加 helm 模板 helm repo add rocketmq-repo https://helm-charts.itboon.top/rocketmq helm repo update rocketmq-repo编写 value.yaml 文件 配置主从节点的个数,例子为单节点 broker:…...

[Docker]入门之docker-compose
一,Docker-compose简介 1,Docker-compose简介 Docker-Compose项目是Docker官方的开源项目,负责实现对Docker容器集群的快速编排。 Docker-Compose将所管理的容器分为三层,分别是工程(project),…...

SAP ABAP中使用函数ALSM_EXCEL_TO_INTERNAL_TABLE读取EXCEL中不同的SHEET数据
SAP提供了标准的读取EXCEL的函数(ALSM_EXCEL_TO_INTERNAL_TABLE),但是此标准函数无法满足对同一EXCEL 进行不同SHEET的数据读取,一下方法就是教你如何通过修改程序来实现ALSM_EXCEL_TO_INTERNAL_TABLE读取多个SHEET; …...

Rust 编程小技巧摘选(6)
目录 Rust 编程小技巧(6) 1. 打印字符串 2. 重复打印字串 3. 自定义函数 4. 遍历动态数组 5. 遍历二维数组 6. 同时遍历索引和值 7. 迭代器方法的区别 8. for_each() 用法 9. 分离奇数和偶数 10. 判断素数(质数) Rust 编程小技巧(6) 1. 打印…...

如何保证Redis缓存和数据库的一致性问题
熟练掌握Redis缓存技术? 那么请问Redis缓存中有几种读写策略,又是如何保证与数据库的一致性问题 今天来聊一聊常用的三种缓存读写策略 Cache Aside Pattern Cache Aside Pattern 是我们平时使用比较多的一个缓存读写模式,比较适合读请求比…...

【数据分析入门】人工智能、数据分析和深度学习是什么关系?如何快速入门 Python Pandas?
目录 一、前言二、数据分析和深度学习的区别三、人工智能四、深度学习五、Pandas六、Pandas数据结构6.1 Series - 序列6.2 DataFrame - 数据框 七、输入、输出7.1 读取/写入CSV7.2 读取/写入Excel7.3 读取和写入 SQL 查询及数据库表 八、调用帮助九、选择(这里可以参考上一篇文…...

JavaScript 里三个点 ... 的用法
// table表头数据let tableHeadData deepClone(data);let tableCacheData [];//表格缓存对比if (!parent && isCacheHeadData) {// 缓存数据keylet tableCacheKey ${window.location.pathname}-${$self.attr(id)}if (localStorage.getItem(tableCacheKey)) {//根据缓…...
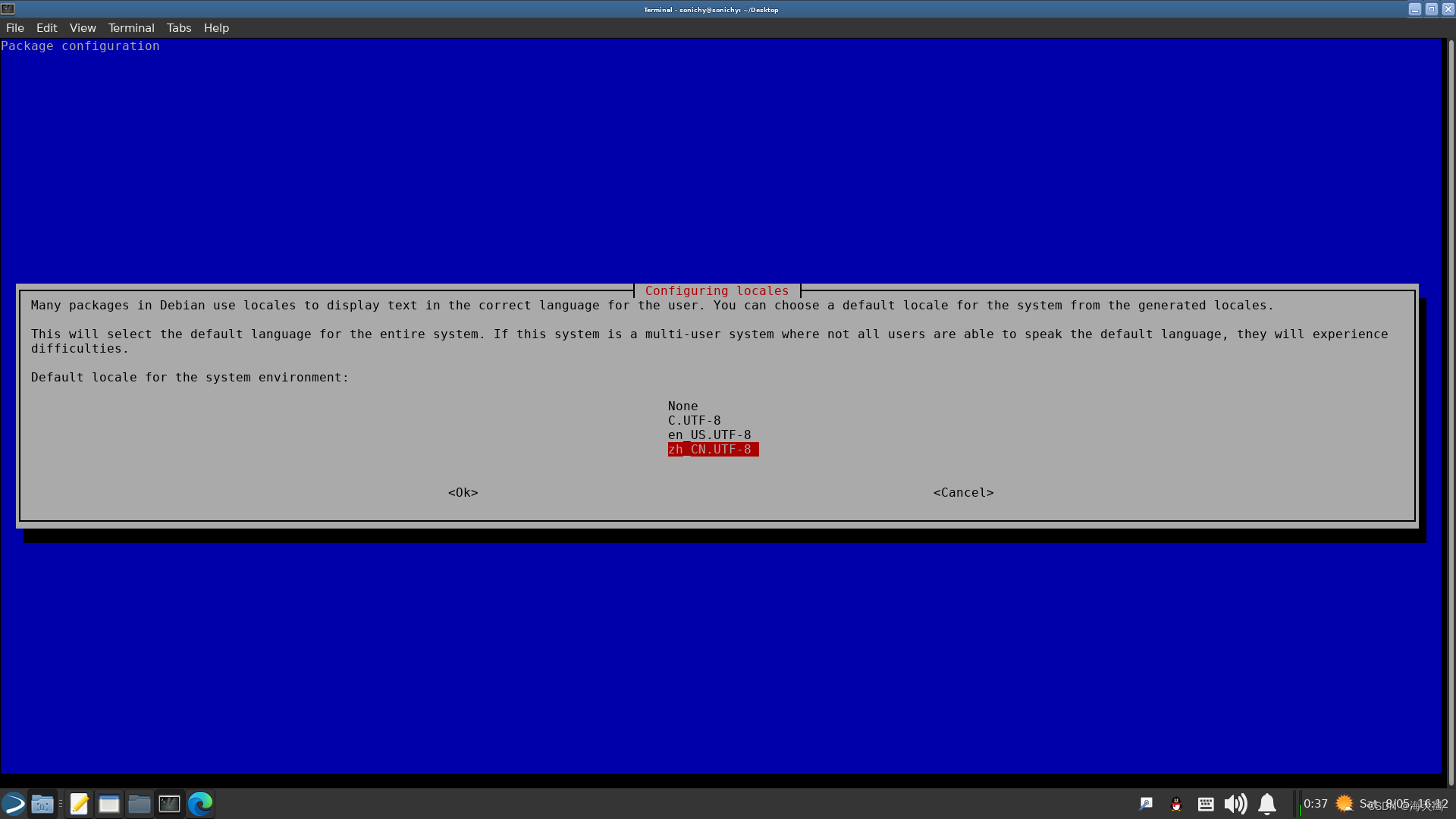
Linux修改系统语言
sudo dpkg-reconfigure locales 按pagedown键,移动红色光标到 zh_CN.UTF-8 UTF-8,空格标记*号(没标记下一页没有这一项),回车。 下一页选择 zh_CN.UTF-8。 如果找不到 dpkg-reconfigure whereis dpkg-reconfigure …...
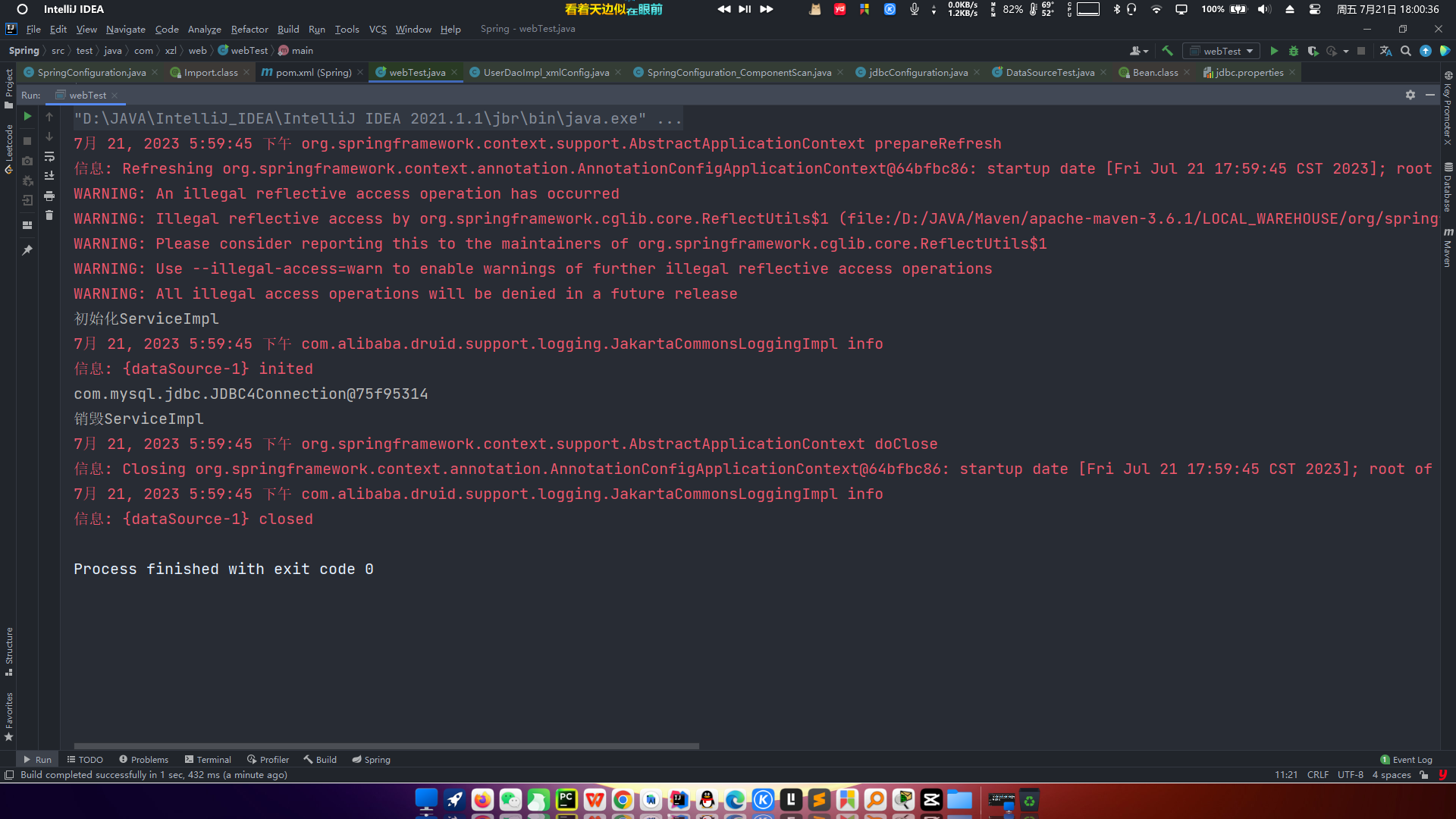
Spring注解开发
目录 1、简介 2、原始注解 2.1、注解种类 2.2、组件扫描 2.3、具体使用 2.3.1、xml配置 2.3.2、注解配置 3、⭐新注解 3.1、新注解种类 3.2、实践 3.3、运行结果 3.4、警告信息 1、简介 Spring框架提供了许多注解,用于在Java类中进行配置和标记…...
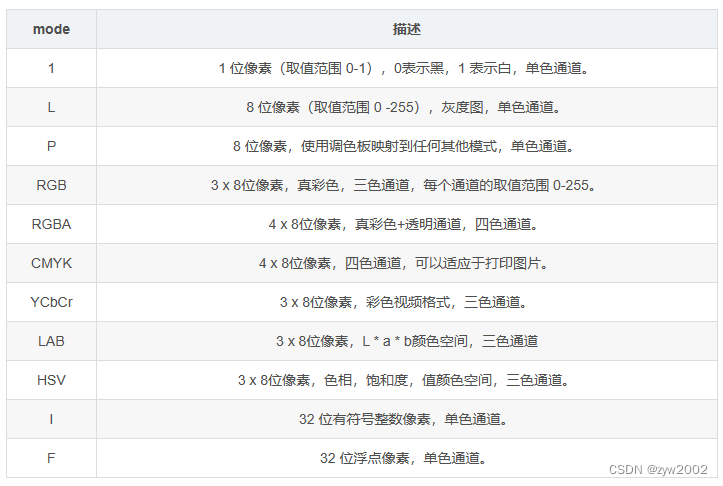
图像处理库(Opencv, Matplotlib, PIL)以及三者之间的转换
文章目录 1. Opencv2. Matplotlib3. PIL4. 三者的区别和相互转换5. Torchvision 中的相关转换库5.1 ToPILImage([mode])5.2 ToTensor5.3 PILToTensor 1. Opencv opencv的基本图像类型可以和numpy数组相互转化,因此可以直接调用torch.from_numpy(img) 将图像转换成t…...

html+Vue+封装axios实现发送请求
在html中使用Vue和Axios时,可以在HTML中引入Vue库和Axios库,然后使用Vue的语法和指令来创建Vue组件和模板。在Vue组件中,你可以使用Axios发送HTTP请求来获取数据,并将数据绑定到Vue模板中进行展示。 <template><div>&…...

GoogLeNet卷积神经网络输出数据形参分析-笔记
GoogLeNet卷积神经网络输出数据形参分析-笔记 分析结果为: 输入数据形状:[10, 3, 224, 224] 最后输出结果:linear_0 [10, 1] [1024, 1] [1] 子空间执行逻辑 def forward_old(self, x):# 支路1只包含一个1x1卷积p1 F.relu(self.p1_1(x))# 支路2包含 1…...

【docker】dockerfile发布springboot项目
目录 一、实现步骤二、示例 一、实现步骤 1.定义父镜像:FROM java:8 2.定义作者信息:MAINTAINER:learn_docker<https://www.docker.com> 3.将jar包添加到容器:ADD jar包名称.jar app.jar 4.定义容器启动执行命令:…...

利用docker run -v 命令实现使用宿主机中没有的命令
利用docker run -v 命令实现使用宿主机中没有的命令 使用容器中的jar命令解压jar包,并将解压内容输出到挂载在宿主机中的目录里 使用容器中的jar命令解压jar包,并将解压内容输出到挂载在宿主机中的目录里 docker run -it --name java -v /www/temp/java…...

【小沐学NLP】在线AI绘画网站(百度:文心一格)
文章目录 1、简介2、文心一格2.1 功能简介2.2 操作步骤2.3 使用费用2.4 若干示例2.4.1 女孩2.4.2 昙花2.4.3 山水画2.4.4 夜晚2.4.5 古诗2.4.6 二次元2.4.7 帅哥 结语 1、简介 当下,越来越多AI领域前沿技术争相落地,逐步释放出极大的产业价值࿰…...

react经验5:访问子组件内容
应用场景 父级需要调用子组件的某函数 实现步骤 案例:创建自定义按钮 button.tsx import { Ref, forwardRef, useImperativeHandle,ReactNode} from "react" declare type ButtonProps {/**按钮文字 */children?: ReactNode,onClick?: () > voi…...
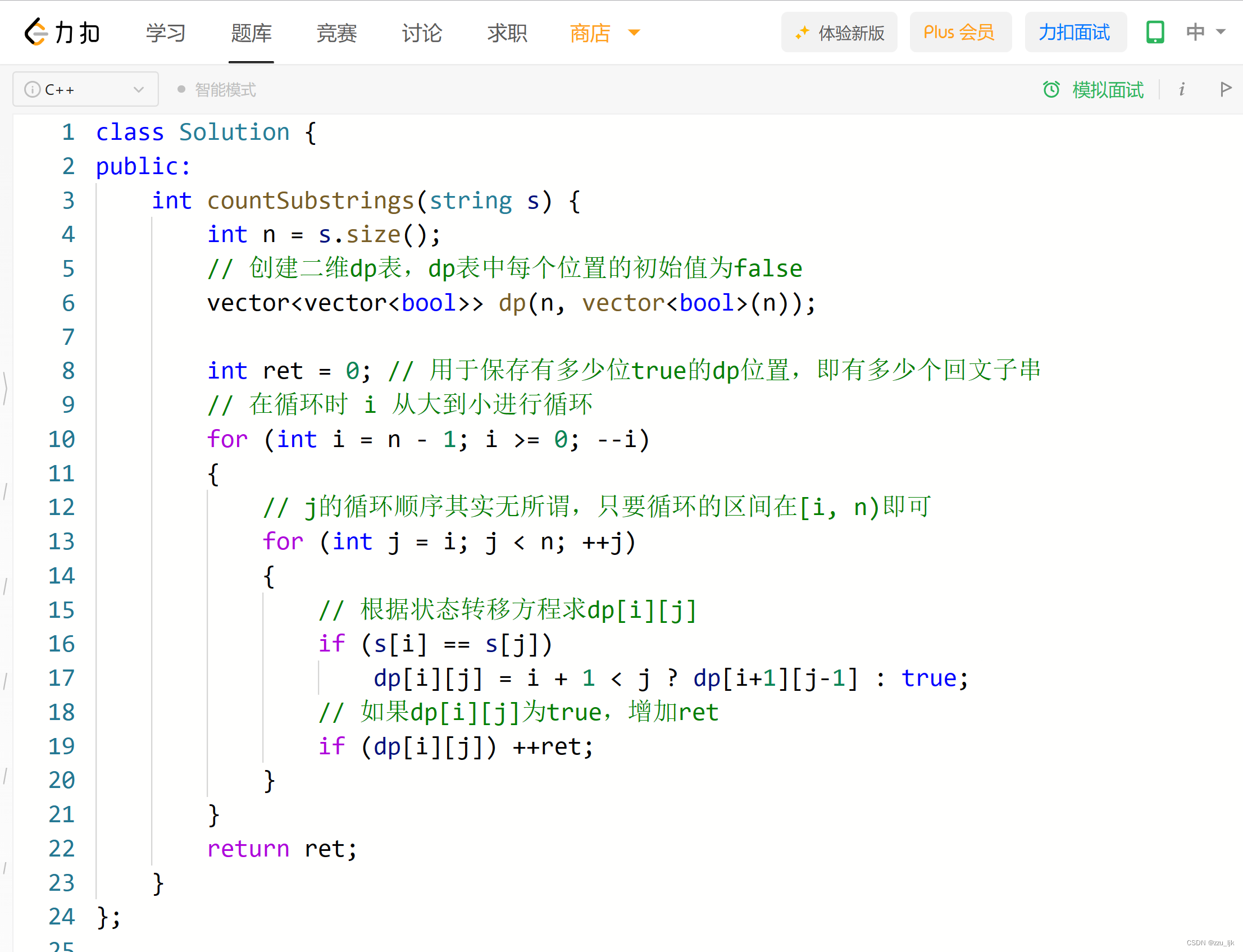
【LeetCode】647. 回文子串
题目链接 文章目录 1. 思路讲解1.1 方法选择1.2 dp表的创建1.3 状态转移方程1.4 填表顺序 2. 代码实现 1. 思路讲解 1.1 方法选择 这道题我们采用动态规划的解法,倒不是动态规划的解法对于这道题有多好,它并不是最优解。但是,这道题的动态…...
 角度制与弧度制的相互转换)
Open3D(C++) 角度制与弧度制的相互转换
目录 一、弧度转角度1、计算公式2、主要函数3、示例代码4、结果展示二、角度转弧度1、计算公式2、主要函数3、示例代码4、结果展示三、归一化到(-PI,PI)1、主要函数<...

【小沐学NLP】在线AI绘画网站(网易云课堂:AI绘画工坊)
文章目录 1、简介1.1 参与方式1.2 模型简介 2、使用费用3、操作步骤3.1 选择模型3.2 输入提示词3.3 调整参数3.4 图片生成 4、测试例子4.1 小狗4.2 蜘蛛侠4.3 人物4.4 龙猫 结语 1、简介 Stable Diffusion是一种强大的图像生成AI,它可以根据输入的文字描述词&#…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
