P1156 垃圾陷阱(背包变形)
垃圾陷阱
题目描述
卡门――农夫约翰极其珍视的一条 Holsteins 奶牛――已经落了到 “垃圾井” 中。“垃圾井” 是农夫们扔垃圾的地方,它的深度为 D D D( 2 ≤ D ≤ 100 2 \le D \le 100 2≤D≤100)英尺。
卡门想把垃圾堆起来,等到堆得与井同样高时,她就能逃出井外了。另外,卡门可以通过吃一些垃圾来维持自己的生命。
每个垃圾都可以用来吃或堆放,并且堆放垃圾不用花费卡门的时间。
假设卡门预先知道了每个垃圾扔下的时间 t t t( 1 ≤ t ≤ 1000 1 \le t \le 1000 1≤t≤1000),以及每个垃圾堆放的高度 h h h( 1 ≤ h ≤ 25 1 \le h \le 25 1≤h≤25)和吃进该垃圾能维持生命的时间 f f f( 1 ≤ f ≤ 30 1 \le f \le 30 1≤f≤30),要求出卡门最早能逃出井外的时间,假设卡门当前体内有足够持续 10 10 10 小时的能量,如果卡门 10 10 10 小时内(不含 10 10 10 小时,维持生命的时间同)没有进食,卡门就将饿死。
输入格式
第一行为两个整数, D D D 和 G G G( 1 ≤ G ≤ 100 1 \le G \le 100 1≤G≤100), G G G 为被投入井的垃圾的数量。
第二到第 G + 1 G+1 G+1 行每行包括三个整数: T T T( 1 ≤ T ≤ 1000 1 \le T \le 1000 1≤T≤1000),表示垃圾被投进井中的时间; F F F( 1 ≤ F ≤ 30 1 \le F \le 30 1≤F≤30),表示该垃圾能维持卡门生命的时间;和 H H H( 1 ≤ H ≤ 25 1 \le H \le 25 1≤H≤25),该垃圾能垫高的高度。
输出格式
如果卡门可以爬出陷阱,输出一个整数,表示最早什么时候可以爬出;否则输出卡门最长可以存活多长时间。
样例 #1
样例输入 #1
20 4
5 4 9
9 3 2
12 6 10
13 1 1
样例输出 #1
13
提示
【样例说明】
卡门堆放她收到的第一个垃圾: h e i g h t = 9 \mathrm{height}=9 height=9;
卡门吃掉她收到的第 2 2 2 个垃圾,使她的生命从 10 10 10 小时延伸到 13 13 13 小时;
卡门堆放第 3 3 3 个垃圾, h e i g h t = 19 \mathrm{height}=19 height=19;
卡门堆放第 4 4 4 个垃圾, h e i g h t = 20 \mathrm{height}=20 height=20。
大致思路
分析题目,我们需要求的答案是时间,于是很自然而然的想到j描述高度或生命,而dp数组存放时间。很显然,这样状态既不完整,也写不出转移方程。而且dp数组存的是当前状态下最大或最小的价值,似乎也不满足。
这时候我们发现,有4个值可能成为状态,高度,生命,物品和时间,难道要dp三维的吗?
再分析题目,每个垃圾都有一个下落的时间,奶牛一定是在垃圾丢下来的时间就处理垃圾的(可以得出这样的最优的),那么物品就可以和时间关联起来了。这时候,我们可以把时间仅仅当作干扰量给剔除了。
需要注意的是,物品的使用顺序并不是随意的,必须按它们下落的时间顺序来先后处理。(这里排一下序即可)
那么j代表什么呢?
一下子我们并不能得出答案。先尝试dp[i][j]dp[i][j]代表前i件物品处理后在j血量时达到的最大高度。
值得一提的是,j血量表示奶牛在暂时不考虑时间时所得到的最大血量
据说这个是叫离线
试着写一下它的状态转移方程
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] + t r a s h [ i ] . h , d p [ i − 1 ] [ j + t r a s h [ i ] . c ] ) dp[i][j]=max(dp[i-1][j]+trash[i].h,dp[i-1][j+trash[i].c]) dp[i][j]=max(dp[i−1][j]+trash[i].h,dp[i−1][j+trash[i].c])
发现这是对的,然而我们再想想,在关于j的一重循环里面,对j的取值我们似乎并不好判断,甚至要枚举很大。
所以我们再尝试讨论dp[i][j]dp[i][j]代表前i件物品处理后在h高度时达到的最大血量。
状态转移
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] + t r a s h [ i ] . c , d p [ i − 1 ] [ j − t r a s h [ i ] . h ] ) dp[i][j]=max(dp[i-1][j]+trash[i].c,dp[i-1][j-trash[i].h]) dp[i][j]=max(dp[i−1][j]+trash[i].c,dp[i−1][j−trash[i].h])
发现这样也是对的,而且j枚举起来也比较方便,于是我们选择这种算法。
AC CODE
#include<bits/stdc++.h>
using namespace std;
int d,g;
struct node{int tim,sur,high;
}a[555];
int f[555];
bool cmp(node aa,node bb){return aa.tim<bb.tim;
}
int main(){cin>>d>>g;for(int i=1;i<=g;i++){cin>>a[i].tim>>a[i].sur>>a[i].high;}sort(a+1,a+1+g,cmp);f[0]=10;for(int i=1;i<=g;i++){for(int j=d;j>=0;j--){if(f[j]>=a[i].tim){if(j+a[i].high>=d){cout<<a[i].tim;return 0;}f[j+a[i].high]=max(f[j],f[j+a[i].high]);f[j]+=a[i].sur;}}}cout<<f[0];return 0;
}
洛谷题解区
附封面(你的名字)
相关文章:

P1156 垃圾陷阱(背包变形)
垃圾陷阱 题目描述 卡门――农夫约翰极其珍视的一条 Holsteins 奶牛――已经落了到 “垃圾井” 中。“垃圾井” 是农夫们扔垃圾的地方,它的深度为 D D D( 2 ≤ D ≤ 100 2 \le D \le 100 2≤D≤100)英尺。 卡门想把垃圾堆起来,…...
[Docker实现测试部署CI/CD----构建成功后钉钉告警(7)]
目录 15、钉钉告警创建项目群,然后添加机器人添加机器人Jenkins 系统配置项目配置修改Jenkinsfile文件,添加钉钉提示信息测试 不修改Jenkinsfile文件,添加钉钉提示信息测试 15、钉钉告警 创建项目群,然后添加机器人 首先需要在钉…...

UE5 半透明覆层材质
文章目录 前言介绍示例1示例2示例3 前言 本文采用虚幻5.2.1版本演示,介绍半透明覆层材质(覆层材质)。 介绍 半透明覆层材质是 UE5.1 版本 更新的功能,使用半透明覆层材质,可以轻松的给物体表面附着一层材质。 在UE5…...
在Raspberry Pi 4上安装Ubuntu 20.04 + ROS noetic(不带显示器)
在Raspberry Pi 4上安装Ubuntu 20.04 ROS noetic(不带显示器) 1. 所需设备 所需设备: 树莓派 4 B 型 wifi microSD 卡:最小 32GB MicroSD 转 SD 适配器 (可选)显示器,鼠标等 2. 树莓派…...
CommStudio for .NET Crack
CommStudio for .NET Crack CommStudio for.NET使您的应用程序可以轻松地使用串行端口和调制解调器进行通信。CommStudio for.NET是一套全面的组件和可视化调试工具,可将远程系统和设备与visual Studio 2005和visual Studio 2008集成。开发与遗留系统和外部设备集成…...
!!!)
蓝桥杯上岸考点清单 (冲刺版)!!!
大家好 我是寸铁💪 真题千千万万遍,蓝桥省一自然现! ✌️ 日更3000里,蓝桥眷顾你 🌟 暴力出奇迹,打表过样例 👊 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &#…...
AI一键生成短视频
AI一键生成推文短视频 阅读时长:10分钟 本文内容: 结合开源AI,一键生成短视频发布到常见的某音,某手平台,狠狠赚一笔 前置知识: 1.基本的 python 编程知识 2.chatGPT 使用过 3.stable diffution 使用过 成果…...
)
基于MATLAB长时间序列遥感数据分析(以MODIS数据处理为例)
MATLAB MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域。 [1] MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂&a…...

postgresql之内存池-AllocsetContext
一、简介 postgresql大部分的内存分配管理都是通过MemoryContext进行操作的, 多个相关的MemoryContext构成了一个树型结构, 多个树构成了一个森林。 实现了三种MemoryContext: SlabContextGenerationContextAllocSetContext 使用全局变量CurrentMemo…...

QT 使用单例模式
目录 1. 单例模式介绍 2.单例模式实现 1. 单例模式介绍 有些时候我们在做 qt 项目的时候,要用到很多类. 例如我们用到的类有 A,B,C,D. 其中,A 是 B,C,D 中都需要用到的类,A 类非常的抢手. 但是,A 类非常的占内存,定义一个 A 对象需要 500M 内存,假如在 B,C,D 中都定义一个 A 类…...

接口测试——postman接口测试(三)
目录 1. postman介绍与安装 2. postman发送get请求 3. postman发送post请求 1. postman介绍与安装 安装网址:Postman安装教程:留言找我要即可 2. postman发送get请求 import pymysql from flask import Flask,request# 这里是mysql的基本连接信息 c…...
react中hooks的理解与使用
一、作用 我们知道react组件有两种写法一种是类组件,另一种是函数组件。而函数组件是无状态组件,如果我们要想改变组件中的状态就无法实现了。为此,在react16.8版本后官方推出hooks,用于函数组件更改状态。 二、常用API 1、use…...
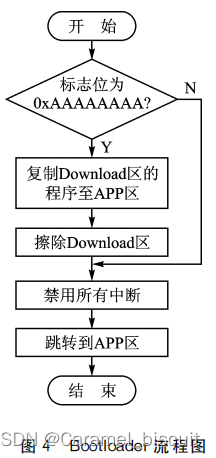
STM32的电动自行车信息采集上报系统(学习)
摘要 针对电动自行车实时监管不便的问题,设计了一种基于STM32的电动自行车信息采集系统,通过获取电池、位置和行驶状态信息并上报到服务器中,实现实时监管。 通过多路串口请求电池、行驶状态和位置信息,以并发方式进行数据接收、…...
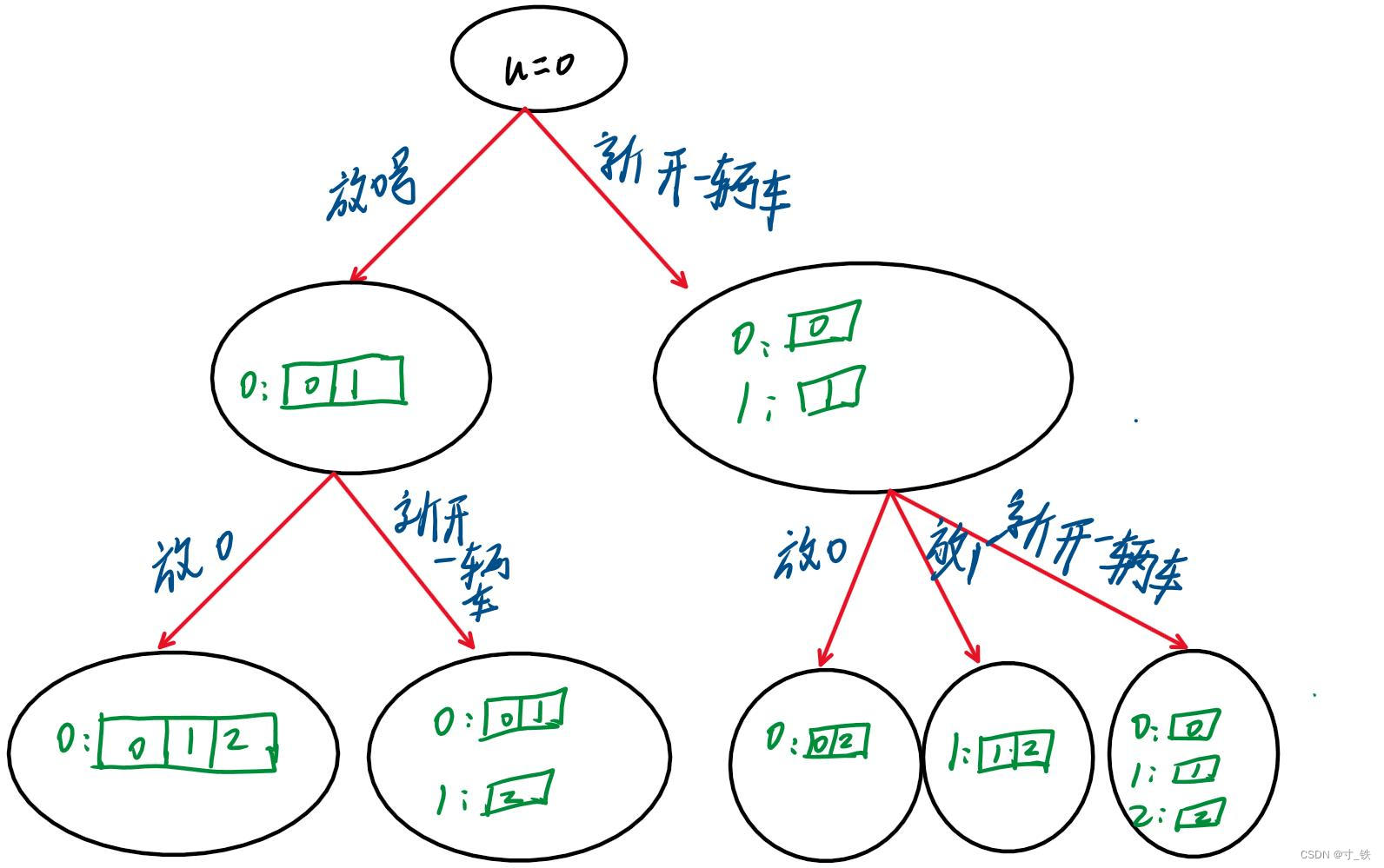
蓝桥杯上岸每日N题 第七期(小猫爬山)!!!
蓝桥杯上岸每日N题 第七期(小猫爬山)!!! 同步收录 👇 蓝桥杯上岸必背!!!(第四期DFS) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &a…...
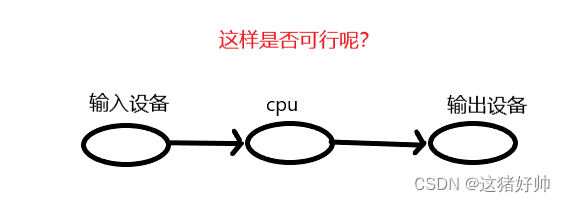
【Linux系统编程】冯诺依曼体系结构
目录 前言 什么是冯诺依曼体系结构? 冯诺依曼体系结构如何进行数据处理的? 存储器在冯诺依曼体系中有什么作用? 冯诺依曼体系结构为什么要这样设计? 冯诺依曼结构总结 前言 相信对于冯诺依曼这个人的名字大家一定不会感到陌…...
数据结构--动态顺序表
文章目录 线性表动态顺序表数组与顺序表 接口实现初始化:尾插:尾删头插头删指定位置插入指定位置删除查找摧毁 完整代码 线性表 线性表是数据结构中最基本、最简单也是最常用的一种数据结构。线性表是指由n个具有相同数据类型的元素组成的有限序列。 线…...
笔试数据结构选填题
目录 卡特兰数Catalan:出栈序列/二叉树数 树 二叉树 N01N2 哈夫曼树(最优二叉树)Huffman 度m的哈夫曼树只有度为0和m的结点:Nm(n-1)/(m-1) 平衡二叉树AVL Nh表示深度为h最少结点数,则N00,N11&#…...

# 鸢尾花的案例学习
# 鸢尾花的案例学习 # 1. 导入小型的数据 from sklearn.datasets import load_iris import numpy as np import pandas as pd import seaborn as sbn import matplotlib.pyplot as plt # 2. 获取数据 irisload_iris() # 3.查看数据print("数据集\n ",len(iris.d…...

线程、进程的区别
线程、进程的区别 在开发中,我们经常听到线程和进程两个概念,它们都是操作系统的基本概念,操作系统以进程为基本单位分配存储器,以线程为基本单位分配CPU。虽然它们有很多相似之处,但是它们也有很大的区别。本文将详细…...

在 Ubuntu 上安装 Docker 桌面
Ubuntu 22.04 (LTS) 安装 Docker 桌面 要成功安装 Docker Desktop,您必须: 满足系统要求拥有 64 位版本的 Ubuntu Jammy Jellyfish 22.04 (LTS) 或 Ubuntu Impish Indri 21.10。对于非 Gnome 桌面环境,必须安装 gnome-terminal:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
