【搜索】DFS连通性模型
算法提高课笔记
目录
- 迷宫
- 题意
- 思路
- 代码
- 红与黑
- 题意
- 思路
- 代码
DFS 的搜索分为两大部分:
- 内部搜索:一个图中从一个点搜到另一个点
- 外部搜索:从一张图(状态)搜到另一张图(状态)
在第一个部分里是图内部点的搜索,每个点只能搜一次,因此搜过的点不需要恢复到原来的(还没被搜过的)状态(意思就是st数组不恢复)
而第二个部分是点的集合之间的搜索,每次搜索完一定要恢复到原有状态才可以进行下一步搜索(意思就是st数组每次需要恢复原状)
迷宫
原题链接
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为#),则看成无法办到。
注意:A、B不一定是两个不同的点。
输入格式
第1行是测试数据的组数 k,后面跟着 k 组输入。
每组测试数据的第1行是一个正整数 n,表示迷宫的规模是 n∗n 的。
接下来是一个 n∗n 的矩阵,矩阵中的元素为.或者#。
再接下来一行是 4 个整数 ha,la,hb,lb,描述 A 处在第 ha 行, 第 la 列,B 处在第 hb 行, 第 lb 列。
注意到 ha,la,hb,lb 全部是从 0 开始计数的。
输出格式
k行,每行输出对应一个输入。
能办到则输出“YES”,否则输出“NO”。
数据范围
1 ≤ n ≤ 100
输入样例
2
3
.##
..#
#..
0 0 2 2
5
.....
###.#
..#..
###..
...#.
0 0 4 0
输出样例
YES
NO
题意
给出一张图两个点,问能不能从一个点走到另一个点
思路
直接bfs遍历看能不能从一个点遍历到另一个
代码
#include <bits/stdc++.h>using namespace std;const int N = 110;int n;
char g[N][N]; // 存图
int xa, ya, xb, yb; // 标记起点终点
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
bool st[N][N]; // 判重bool dfs(int x, int y)
{if (g[x][y] == '#') return false;if (x == xb && y == yb) return true;st[x][y] = true;for (int i = 0; i < 4; i ++ ) // 遍历四个操作{int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n) continue; // 位置不合法if (st[a][b]) continue; // 已遍历if (dfs(a, b)) return true;} return false;
}int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);int t;cin >> t;while (t -- ){cin >> n;for (int i = 0; i < n; i ++ ) cin >> g[i];cin >> xa >> ya >> xb >> yb;memset(st, false, sizeof st);if (dfs(xa, ya)) cout << "YES\n";else cout << "NO\n";}
}
红与黑
原题链接
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。
在接下来的 H 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围
1 ≤ W , H ≤ 20
输入样例
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例
45
题意
一个图分为红黑方块,问某一个黑方块的连通块个数
思路
本质上是个Flood Fill问题,可以用BFS实现
用DFS也是一样的,只是搜索顺序不一样
代码
#include <bits/stdc++.h>using namespace std;const int N = 25;int n, m;
char g[N][N]; // 存图
bool st[N][N]; // 判重
int dx[4] = {0, 0, -1, 1}, dy[4] = {1, -1, 0, 0};int dfs(int x, int y)
{int cnt = 1;st[x][y] = true;for (int i = 0; i < 4; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m) continue; // 位置不合法if (g[a][b] != '.') continue; // 不是黑色的if (st[a][b]) continue; // 已遍历cnt += dfs(a, b);}return cnt;
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> m >> n, n || m){for (int i = 0; i < n; i ++ ) cin >> g[i];int x, y;for (int i = 0; i < n; i ++ ) for (int j = 0; j < m; j ++ )if (g[i][j] == '@') // 找起点{x = i;y = j;}memset(st, false, sizeof st);cout << dfs(x, y) << '\n';}
}
相关文章:

【搜索】DFS连通性模型
算法提高课笔记 目录 迷宫题意思路代码 红与黑题意思路代码 DFS 的搜索分为两大部分: 内部搜索:一个图中从一个点搜到另一个点外部搜索:从一张图(状态)搜到另一张图(状态) 在第一个部分里是图…...

项目优化后续 ,手撸一个精简版VUE项目框架!
之前说过项目之前用的vben框架,在优化完性能后打包效果由原来的纯代码96M变成了56M,后续来啦,通过更换框架,代码压缩到了36M撒花~ 现在就来详细说说是怎么手撸一个框架的! 方案: 搭建一套 vite vue3 a…...
【深度学习笔记】TensorFlow 基础
在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。…...

面试题-springcloud中的负载均衡是如何实现的?
一句话导读 Springcloud中的负载均衡是通过Ribbon实现的,自带有很多负载均衡策略,如:包括轮询(Round Robin)、随机(Random)、加权轮询(Weighted Round Robin)、加权随机&…...

flink的ProcessWindowFunction函数的三种状态
背景 在处理窗口函数时,ProcessWindowFunction处理函数可以定义三个状态: 富函数getRuntimeContext.getState, 每个key每个窗口的状态context.windowState(),每个key的状态context.globalState,那么这几个状态之间有什么关系呢? …...
day50-springboot+ajax分页
分页依赖: <dependency> <groupId>com.github.pagehelper</groupId> <artifactId>pagehelper-spring-boot-starter</artifactId> <version>1.0.0</version> </dependency> 配置: …...
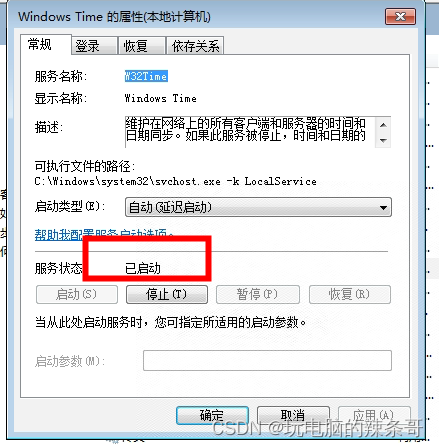
Win7 专业版Windows time w32time服务电脑重启后老是已停止
环境: Win7 专业版 问题描述: Win7 专业版Windows time w32time服务电脑重启后老是已停止 解决方案: 1.检查启动Remote Procedure Call (RPC)、Remote Procedure Call (RPC) Locator,DCOM Server Process Launcher这三个服务是…...
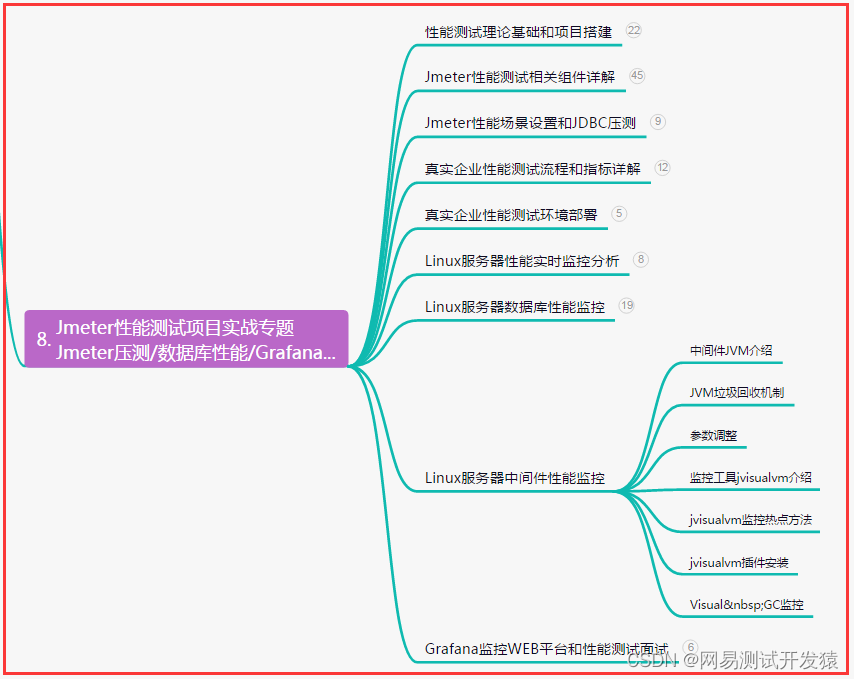
全网最强,接口自动化测试-token登录关联实战总结(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在PC端登录公司的…...
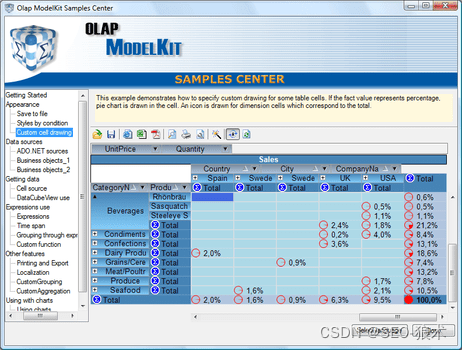
OLAP ModelKit Crack,ADO.NET和IList
OLAP ModelKit Crack,ADO.NET和IList OLAP ModelKit是一个多功能的.NET OLAP组件,用C#编写,只包含100%托管代码。它具有XP主题的外观,并能够使用任何.NET数据源(ADO.NET和IList)。借助任何第三方组件(尤其是图表组件)呈现数据的能力扩展了产品…...
4 三组例子,用OpenCV玩转图像-AI-python
读取,缩放,旋转,写入图像 首先导入包,为了显示导入matplotlib/为了在matplotlib显示 导入CV2/查看版本 导入图片/查看图片类型 图片数组 数组大小 对于opencv通道顺序蓝色B、绿色G、红色R matplotlib通道顺序为 红色R、绿色G、蓝…...

计算机网络-三种交换方式
计算机网络-三种交换方式 电路交换(Circuit Switching) 电话交换机接通电话线的方式称为电路交换从通信资源分配的角度来看,交换(Switching)就是按照某种方式动态的分配传输线路的资源 电话交换机 为了解决电话之间通信两两之间连线过多,所以产生了电话…...
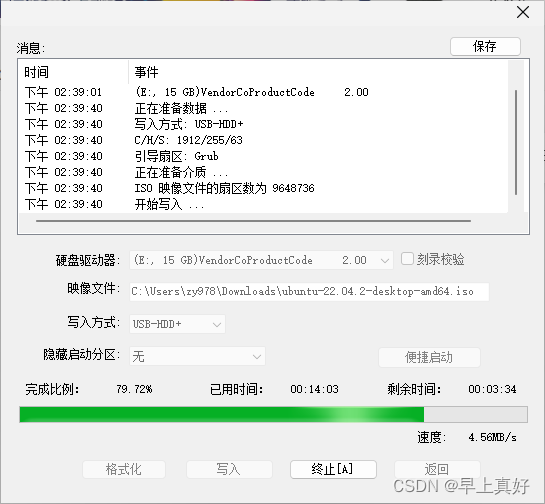
03 制作Ubuntu启动盘
1 软碟通 我是用软碟通制作启动盘。安装软碟通时一定要把虚拟光驱给勾选上,其余两个可以看你心情。 2 镜像文件 我使用清华镜像网站找到的Ubuntu镜像文件。 Index of /ubuntu-releases/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 请自己选择镜像…...

【JavaSE】String类中常用的字符串方法(超全)
目录 1.求字符串的长度 2.判断字符串是否为空 3.String对象的比较 3.1 判断字符串是否相同 3.2 比较字符串大小 3.3 忽略大小写比较 4.字符串查找 5.转化 5.1 数值和字符串转化 5.1.1 数字转字符串 valueof 5.1.2 valueOf的其他用法 5.1.3 字符串转数字 5.2 大小写转…...
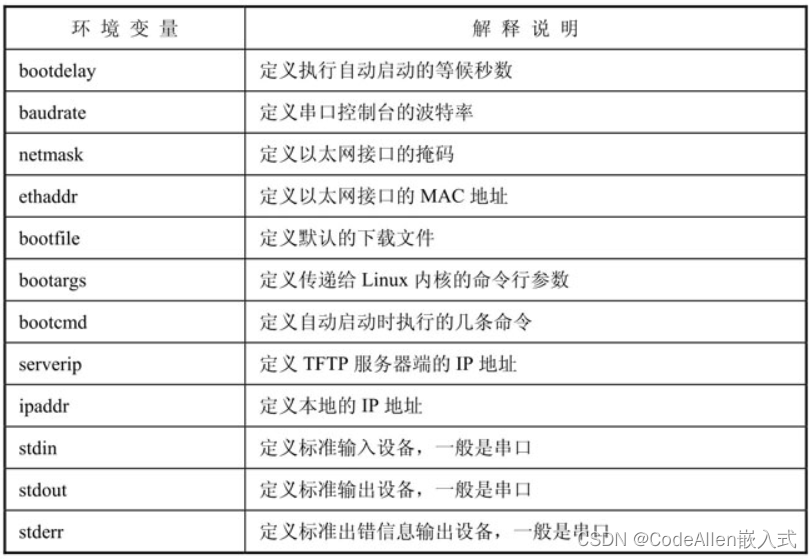
Bootload U-Boot分析
Bootloader是在操作系统运行之前执行的一段小程序。通过这段小程序可以初始化硬件设备、建立内存空间的映射表,从而建立适当的系统软硬件环境,为最终调用操作系统内核做好准备。 对于嵌入式系统,Bootloader是基于特定硬件平台来实现的。因此…...

以公益之行,筑责任之心——2023年中创算力爱心公益助学活动
捐资助学是一项功在当代、利在千秋的义举。 高考录取工作已经开始,一张张高校录取通知书也陆续送达各位准大学生手中。当他们怀揣着对大学的好奇与憧憬,准备迈进理想的大学时,还有一群人,他们渴望知识,却因经济困难而…...

【机器学习】处理样本不平衡的问题
文章目录 样本不均衡的概念及影响样本不均衡的解决方法样本层面欠采样 (undersampling)过采样数据增强 损失函数层面模型层面采样集成学习 决策及评估指标 样本不均衡的概念及影响 机器学习中,样本不均衡问题经常遇到,比如在金融…...
Android前沿技术?Jetpack如何?
Jetpack Compose是Android开发领域的一项前沿技术,它提供了一种全新的方式来构建用户界面。近年来,Jetpack Compose在各大招聘等网站上的招聘岗位逐渐增多,薪资待遇也相应提高。本文将从招聘岗位的薪资与技术要求入手,分析Jetpack…...

为react项目添加开发/提交规范(前端工程化、eslint、prettier、husky、commitlint、stylelint)
因历史遗留原因,接手的项目没有代码提醒/格式化,包括 eslint、pretttier,也没有 commit 提交校验,如 husky、commitlint、stylelint,与其期待自己或者同事的代码写得完美无缺,不如通过一些工具来进行规范和…...
)
小研究 - MySQL 数据库安全加固技术的研究(一)
随着信息系统的日益普及,后台数据库的安全问题逐步被人们重视起来。以当下热门的MySQL 数据库为例,通过分析数据库的安全机制以及总结数据库面临的安全风险,针对性地提出了相应的加固策略,为数据库的安全加固工作提供了技术支撑。…...

linux安装redis带图详细
如何在Linux系统中卸载Redis 一、使用apt-get卸载Redis sudo apt-get purge redis-server如果使用apt-get安装Redis,可以使用apt-get purge命令完全卸载Redis。其中,purge命令会不仅仅删除Redis二进制文件,还会删除配置文件、数据文件和日志…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
