最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树
最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。
换句话说,最小生成树是原图中的一个子图,它包含所有顶点,并且连接所有顶点的边的权重之和最小。
最小生成树的定义有以下特点:
- 最小生成树是无向图的一种树形结构,其中没有环(即没有闭合路径)。
- 最小生成树包含图中的所有顶点,但只包含足够数量的边来连接这些顶点,使得树成为一个连通的图。
- 最小生成树的总权重(边的权重之和)应该最小,即从所有可能的生成树中选择边权重之和最小的树。
最小生成树算法的目标是找到满足上述条件的最优解,常用的算法包括Prim算法和Kruskal算法。这些算法可以在连通无向图中找到最小生成树,并且在不同应用中具有重要的应用价值,如网络设计、电路布线、城市规划等。
2.Prim算法
Prim算法是一种用于求解最小生成树的贪心算法。
它从图的某个顶点开始,逐步将距离当前生成树最近的顶点加入生成树,直到所有顶点都被包含在最小生成树中。
Prim算法的基本思想是通过不断地选择与当前生成树最近的顶点,并将该顶点与生成树中的一个顶点连接,来逐步构造最小生成树。
Prim算法的步骤如下:
- 选择一个起始顶点作为初始生成树,将该顶点加入生成树中。
- 初始化一个辅助数据结构(如优先队列或最小堆),用于存储与当前生成树相连的边,并按边的权重值排序。
- 在辅助数据结构中选择权重最小的边(即与当前生成树最近的边),将其相连的顶点加入生成树,并将该边从辅助数据结构中移除。
- 重复步骤3,直到所有顶点都被包含在生成树中。
Prim算法的过程可以保证生成的树是连通的,并且是最小生成树。它的时间复杂度取决于辅助数据结构的实现方式,一般情况下为O(ElogV),其中E是图的边数,V是图的顶点数。
3.Kruskal算法
Kruskal算法也是一种用于求解最小生成树的贪心算法。
它与Prim算法类似,但在选择边的方式上略有不同。Kruskal算法是基于边来构建最小生成树的,而不是基于顶点。
Kruskal算法的基本思想是从图的边集合中选择权重最小的边,并将其加入生成树中,直到生成树中包含了所有的顶点为止。
在选择边的过程中,需要保证生成树不形成环路,因此可以使用并查集来辅助判断两个顶点是否处于同一个连通分量。
Kruskal算法的步骤如下:
- 将图的所有边按照权重值从小到大排序。
- 初始化一个并查集,用于判断顶点之间的连通性。
- 依次遍历排序后的边集合,如果当前边的两个顶点不在同一个连通分量中,就将该边加入生成树,并合并两个顶点所在的连通分量。
- 重复步骤3,直到生成树包含了所有顶点。
Kruskal算法的过程可以保证生成的树是连通的,并且是最小生成树。它的时间复杂度取决于边排序和并查集操作的复杂度,一般情况下为O(ElogE + ElogV),其中E是图的边数,V是图的顶点数。
相关文章:
)
最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树 最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。 换句话说,最小生成树是原图中的一个子图&#…...

4、数据清洗
4、数据清洗 前面我们处理的数据实际上都是已经被处理好的规整数据,但是在大数据整个生产过程中,需要先对数据进行数据清洗,将杂乱无章的数据整理为符合后面处理要求的规整数据。 数据去重 1.删除重复数据groupby().count():可以…...

Python-OpenCV 图像的基础操作
图像的基础操作 获取图像的像素值并修改获取图像的属性信息图像的ROI区域图像通道的拆分及合并图像扩边填充图像上的算术运算图像的加法图像的混合图像的位运算 获取图像的像素值并修改 首先读入一副图像: import numpy as np import cv2# 1.获取并修改像素值 # 读…...

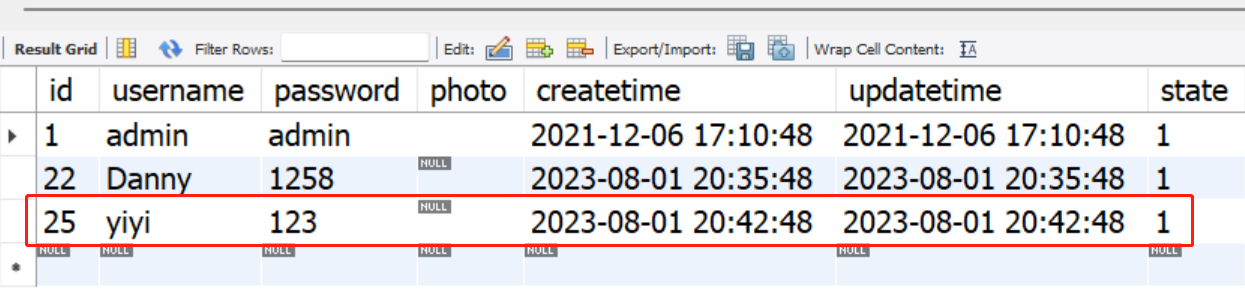
test111
step3:多线程task 首先,实现两个UserService和AsyncUserService两个服务接口: package com.example.demospringboot.service;public interface UserService {void checkUserStatus(); }package com.example.demospringboot.service.impl;im…...
17. Spring 事务
目录 1. 事务定义 2. MySQL 中的事务使用 3. 没有事务时的插入 4. Spring 编程式事务 5. Spring 声明式事务 5.1 Transactional 作用范围 5.2 Transactional 参数说明 5.3 Transactional 工作原理 1. 事务定义 将⼀组操作封装成一个执行单元(封装到一起…...

【C# 基础精讲】运算符和表达式
在C#编程中,运算符和表达式是构建复杂逻辑的关键元素。运算符用于执行各种数学、逻辑和其他操作,而表达式则由运算符、变量、常量和函数组成,用于生成计算结果。本文将详细介绍C#中常见的运算符和表达式的概念,以及它们在程序中的…...

【搜索】DFS连通性模型
算法提高课笔记 目录 迷宫题意思路代码 红与黑题意思路代码 DFS 的搜索分为两大部分: 内部搜索:一个图中从一个点搜到另一个点外部搜索:从一张图(状态)搜到另一张图(状态) 在第一个部分里是图…...

项目优化后续 ,手撸一个精简版VUE项目框架!
之前说过项目之前用的vben框架,在优化完性能后打包效果由原来的纯代码96M变成了56M,后续来啦,通过更换框架,代码压缩到了36M撒花~ 现在就来详细说说是怎么手撸一个框架的! 方案: 搭建一套 vite vue3 a…...
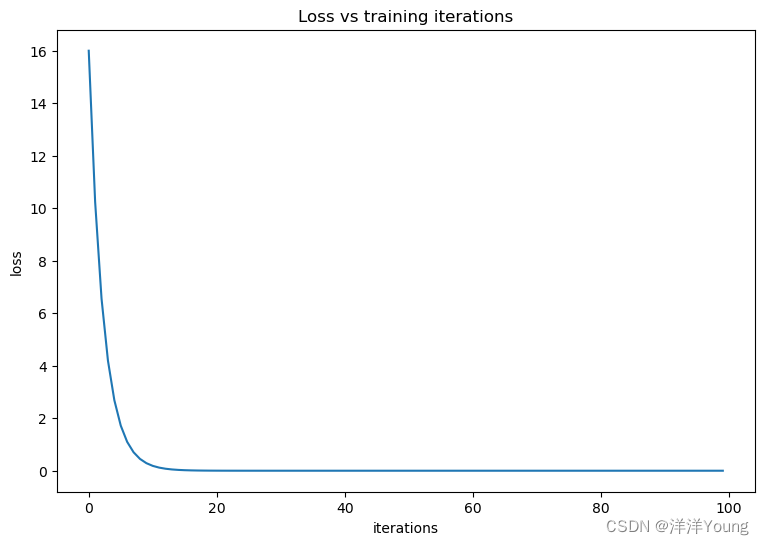
【深度学习笔记】TensorFlow 基础
在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。…...

面试题-springcloud中的负载均衡是如何实现的?
一句话导读 Springcloud中的负载均衡是通过Ribbon实现的,自带有很多负载均衡策略,如:包括轮询(Round Robin)、随机(Random)、加权轮询(Weighted Round Robin)、加权随机&…...

flink的ProcessWindowFunction函数的三种状态
背景 在处理窗口函数时,ProcessWindowFunction处理函数可以定义三个状态: 富函数getRuntimeContext.getState, 每个key每个窗口的状态context.windowState(),每个key的状态context.globalState,那么这几个状态之间有什么关系呢? …...
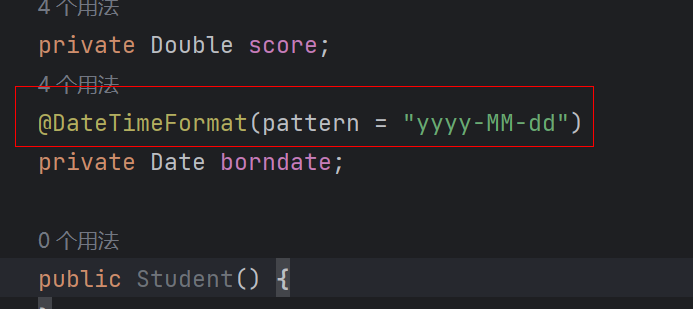
day50-springboot+ajax分页
分页依赖: <dependency> <groupId>com.github.pagehelper</groupId> <artifactId>pagehelper-spring-boot-starter</artifactId> <version>1.0.0</version> </dependency> 配置: …...
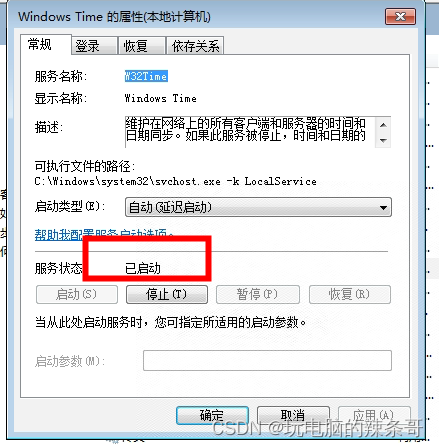
Win7 专业版Windows time w32time服务电脑重启后老是已停止
环境: Win7 专业版 问题描述: Win7 专业版Windows time w32time服务电脑重启后老是已停止 解决方案: 1.检查启动Remote Procedure Call (RPC)、Remote Procedure Call (RPC) Locator,DCOM Server Process Launcher这三个服务是…...
全网最强,接口自动化测试-token登录关联实战总结(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在PC端登录公司的…...
OLAP ModelKit Crack,ADO.NET和IList
OLAP ModelKit Crack,ADO.NET和IList OLAP ModelKit是一个多功能的.NET OLAP组件,用C#编写,只包含100%托管代码。它具有XP主题的外观,并能够使用任何.NET数据源(ADO.NET和IList)。借助任何第三方组件(尤其是图表组件)呈现数据的能力扩展了产品…...
4 三组例子,用OpenCV玩转图像-AI-python
读取,缩放,旋转,写入图像 首先导入包,为了显示导入matplotlib/为了在matplotlib显示 导入CV2/查看版本 导入图片/查看图片类型 图片数组 数组大小 对于opencv通道顺序蓝色B、绿色G、红色R matplotlib通道顺序为 红色R、绿色G、蓝…...

计算机网络-三种交换方式
计算机网络-三种交换方式 电路交换(Circuit Switching) 电话交换机接通电话线的方式称为电路交换从通信资源分配的角度来看,交换(Switching)就是按照某种方式动态的分配传输线路的资源 电话交换机 为了解决电话之间通信两两之间连线过多,所以产生了电话…...
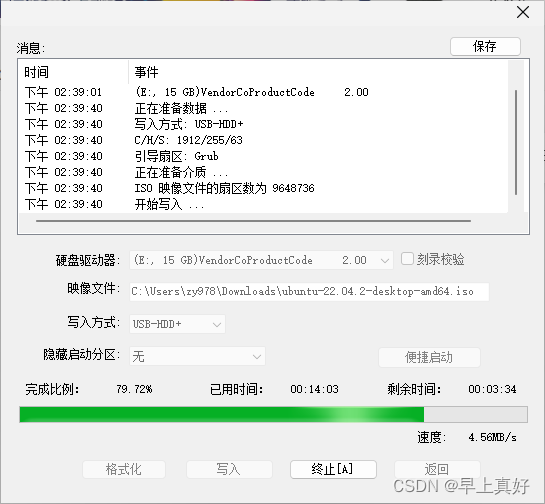
03 制作Ubuntu启动盘
1 软碟通 我是用软碟通制作启动盘。安装软碟通时一定要把虚拟光驱给勾选上,其余两个可以看你心情。 2 镜像文件 我使用清华镜像网站找到的Ubuntu镜像文件。 Index of /ubuntu-releases/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 请自己选择镜像…...

【JavaSE】String类中常用的字符串方法(超全)
目录 1.求字符串的长度 2.判断字符串是否为空 3.String对象的比较 3.1 判断字符串是否相同 3.2 比较字符串大小 3.3 忽略大小写比较 4.字符串查找 5.转化 5.1 数值和字符串转化 5.1.1 数字转字符串 valueof 5.1.2 valueOf的其他用法 5.1.3 字符串转数字 5.2 大小写转…...
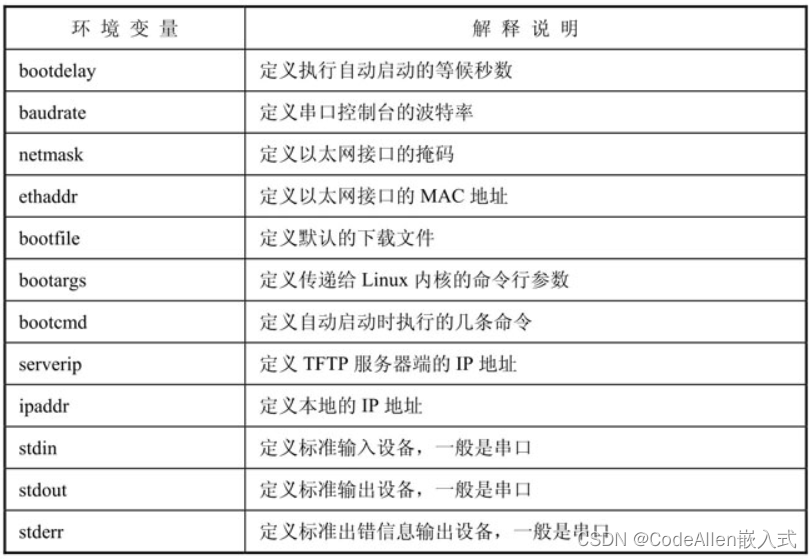
Bootload U-Boot分析
Bootloader是在操作系统运行之前执行的一段小程序。通过这段小程序可以初始化硬件设备、建立内存空间的映射表,从而建立适当的系统软硬件环境,为最终调用操作系统内核做好准备。 对于嵌入式系统,Bootloader是基于特定硬件平台来实现的。因此…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
