简单易懂的Transformer学习笔记
1. 整体概述
2. Encoder
2.1 Embedding
2.2 位置编码
2.2.1 为什么需要位置编码
2.2.2 位置编码公式
2.2.3 为什么位置编码可行
2.3 注意力机制
2.3.1 基本注意力机制
2.3.2 在Trm中是如何操作的
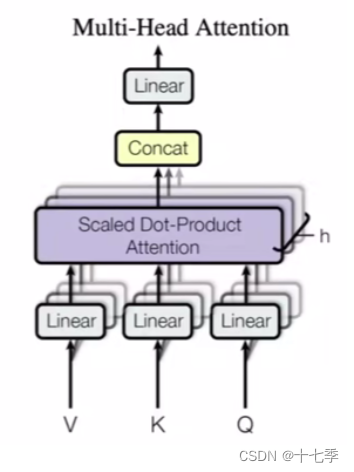
2.3.3 多头注意力机制
2.4 残差网络
2.5 Batch Normal & Layer Narmal
2.5.1 Batch Normal
2.5.2 Layer Normal
3. Decoder
3.1 Mask
3.2 交互层
1. 整体概述
Transformer模型首次提出是在论文Attention is All You Need中。在论文中,Transformer被用来实现机器翻译的工作。相较于RNN难以并行处理信息与CNN窗口短难以处理长序列的缺点,Transformer具有更高的效率与更加优秀的性能。
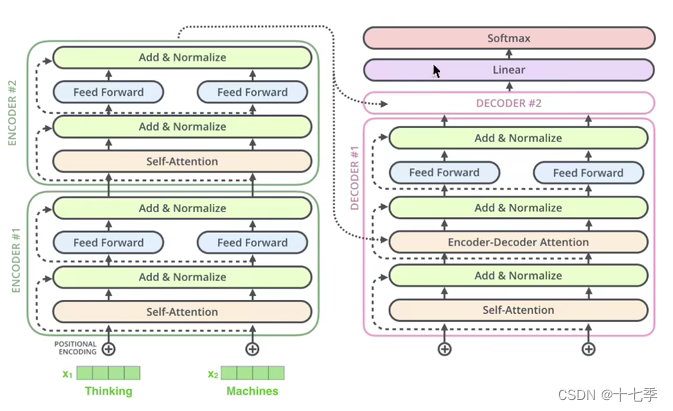
总体来看,Transformer由编码器与解码器两部分组成。
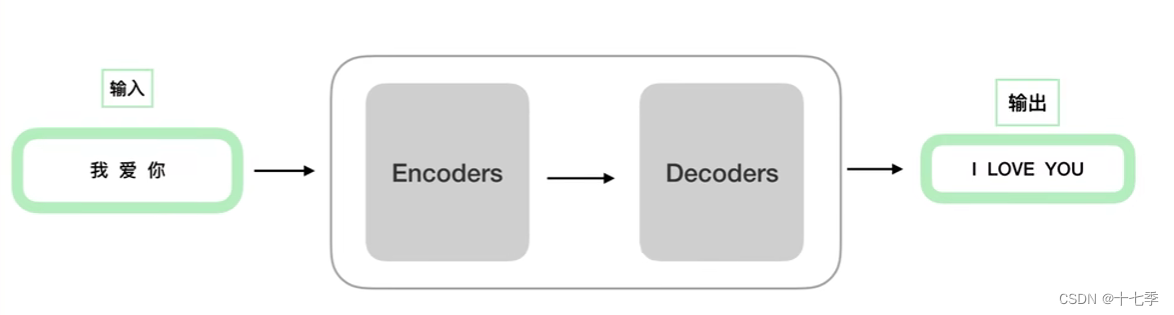
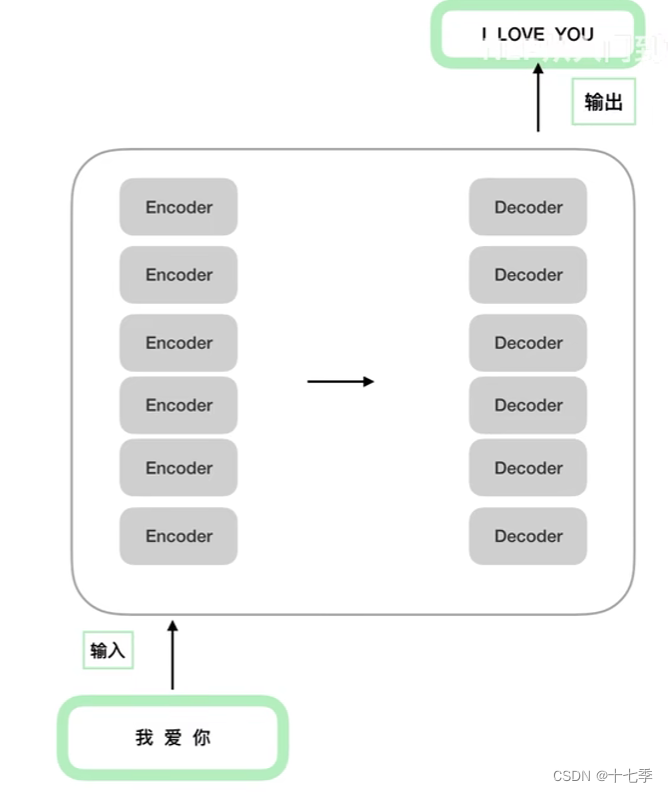
其中,Encoder与Decoder是可以堆叠N(论文中N=6)层的,这些层结构相同,参数独立。
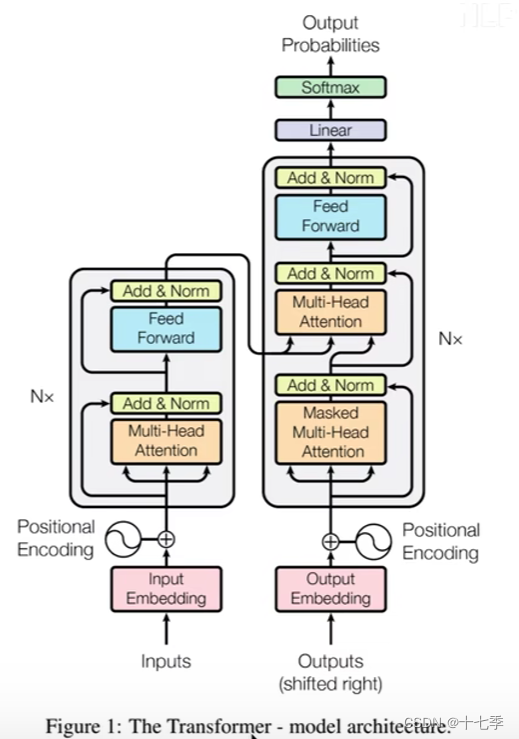
论文中的Transformer架构如下,下文将针对各个环节进行解释。
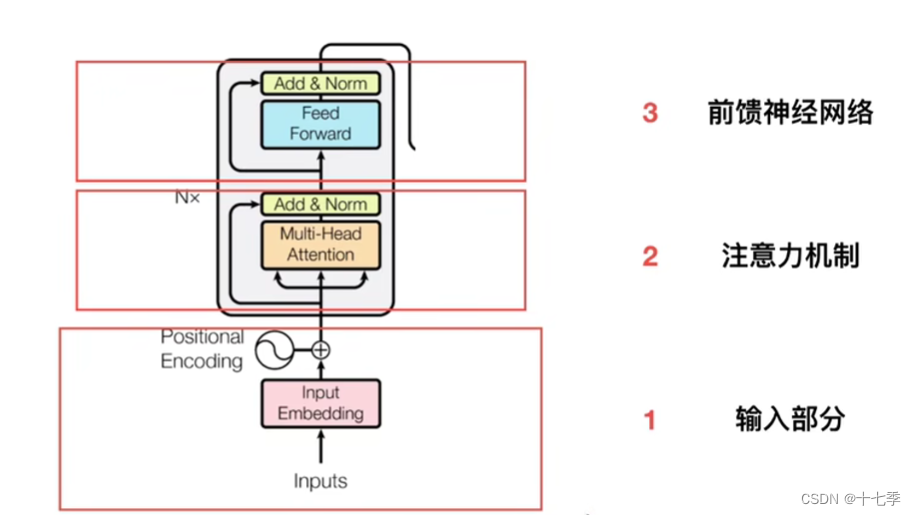
2. Encoder
分为三个部分,输入部分、注意力机制与前馈神经网络。将输入送入
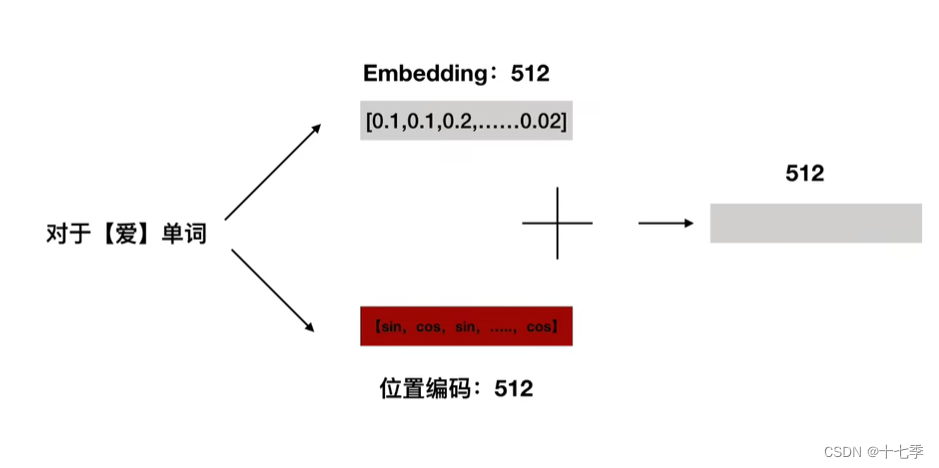
(词嵌入层),与位置编码对位相加。之后进行多头注意力机制处理,进入残差网络并将结果进行
。之后进入双层全连接网络,并对结果进行残差和正则化处理。
论文中的有6层堆叠网络,其中每层有2层子层网络。
2.1 Embedding
可以看作是一个查找表,用来获取每个单词的学习向量表示。神经网络通过数字进行学习,所以将每个单词映射到一个连续值的向量来表示该单词。
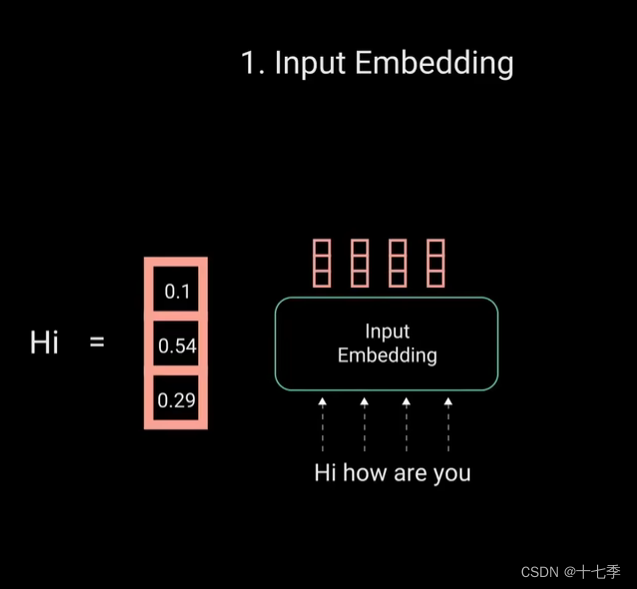
2.2 位置编码
2.2.1 为什么需要位置编码
不同于RNN的按时间线串行处理,Transformer是并行处理的。为了保存序列顺序,引入位置编码。
2.2.2 位置编码公式
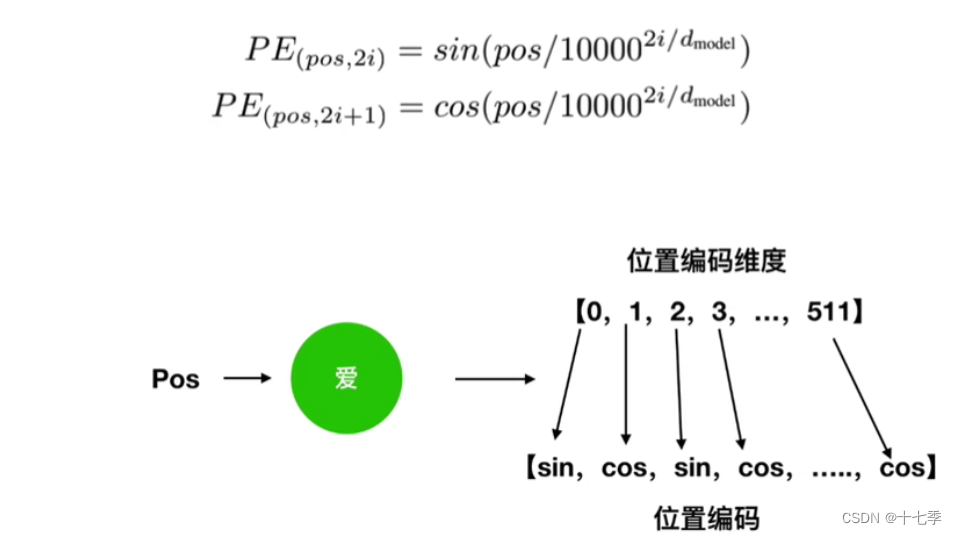
将Embedding与位置编码相加得到的值作为下面环节的输入。
2.2.3 为什么位置编码可行
对于一个特定位置的维的位置向量,借助三角函数的性质
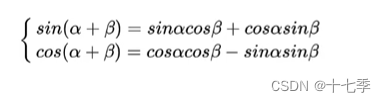
我们可以得到:
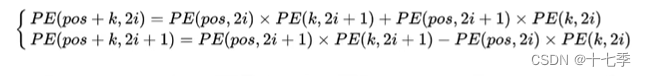
可以看出,位置的位置向量的某一维
或
,可以由
位置与
位置的位置向量的
与
为的线性组合表示。这意味着向量中蕴含了相对位置信息(但该相对位置信息会在注意力机制处消失)。
2.3 注意力机制
2.3.1 基本注意力机制
注意力即关注点。比如给你一张包含婴儿的图片,并提问婴儿在干嘛,此时你对图片中各部分的关注度是不同的,可能对婴儿的脸与手的部分关注度更高,而对图片边缘部分则关注度较低。
论文中给出的注意力公式如下:
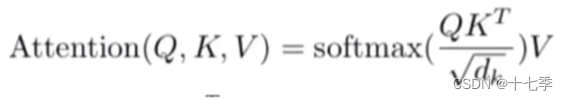
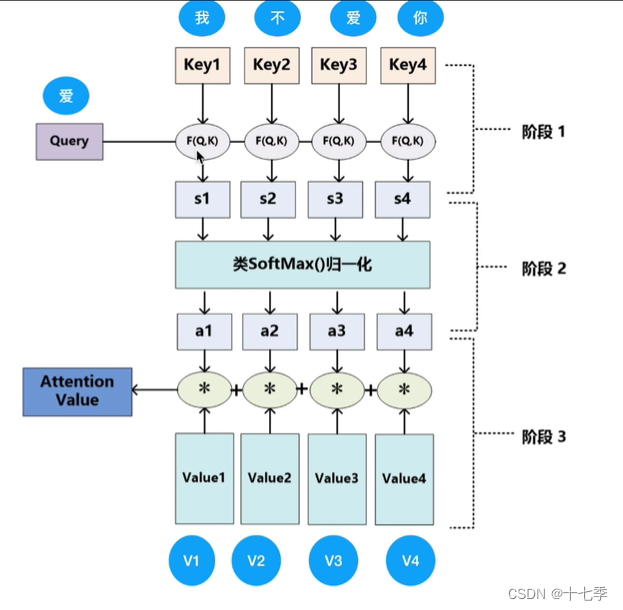
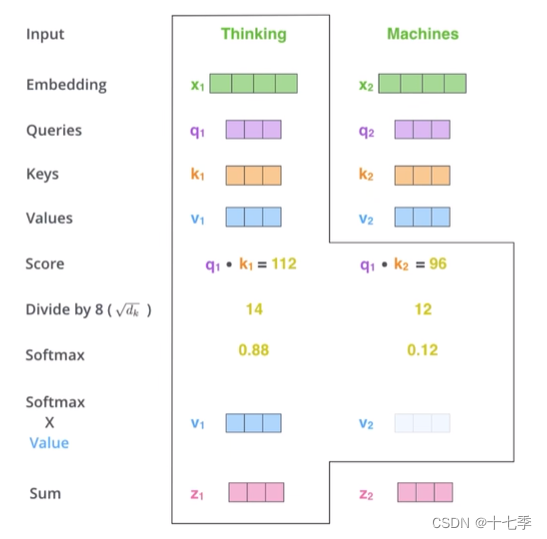
下面以输入“我不爱你”为例解释公式。如图,阶段1中向量Q与向量K点乘,点乘得到的值可以反映两个向量之间的相似程度。阶段2对阶段1中得到的值做了类softmax的归一化处理。除以可以防止值向两端偏导致梯度消失。阶段3中将阶段2得到的值分别与对应的value值相乘,最后将这些结果相加得到了Attention Value。
以上是nlp的举例,cv中也类似,图像的分割可类比词的分割。
2.3.2 在Trm中是如何操作的
首先,我们需要由单词向量获取的值。对于词向量
,将其分别与
相乘(注意这里与所有的词向量相乘的都是同一套
参数),可以得到
。接着,计算
的相似度,得到
的值。 在实际代码中,通常使用矩阵表示,方便并行。
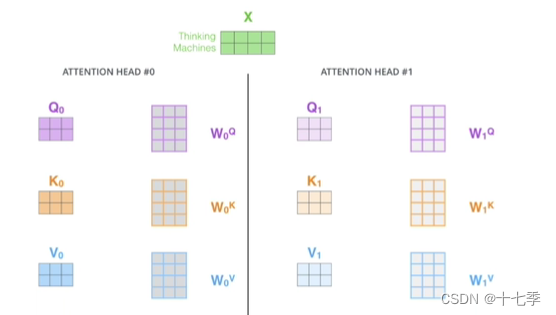
2.3.3 多头注意力机制
将词向量与不同的参数相乘,可以得到多组值。亦即将
投影到低维
次,做j次注意力函数,合并每个输出得到最终输出。
类似于里的多通道输出,使得Trm有可学习的参数。
2.4 残差网络
残差网络将原先的输出与输入
对位相加。要求输入与输出维度相同,论文中设置维度为512。
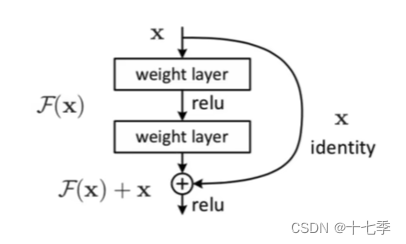
将上图简化如下:
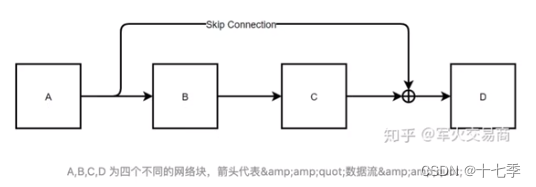
根据后向传播的链式法则:,
而,
所以。
连乘容易导致梯度消失,又因为连乘前有“1”在,所以偏导不易为0。因此,使用残差可以得到有效防止梯度消失,从而得到更深的网络。
2.5 Batch Normal & Layer Narmal
2.5.1 Batch Normal
针对不同样本的同一维度(特征)进行标准化处理,使得均值为0,方差为1。
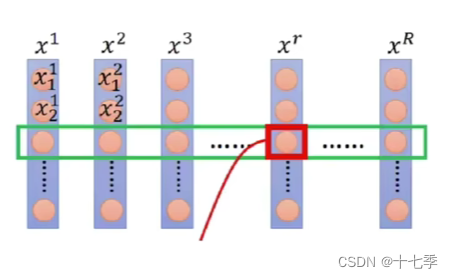
缺点:
1.当较小时,效果差(此时每个
里的样本的均值和方差无法替代整体)。
2.在中效果比较差,因为会出现词向量长度不一样的情况。
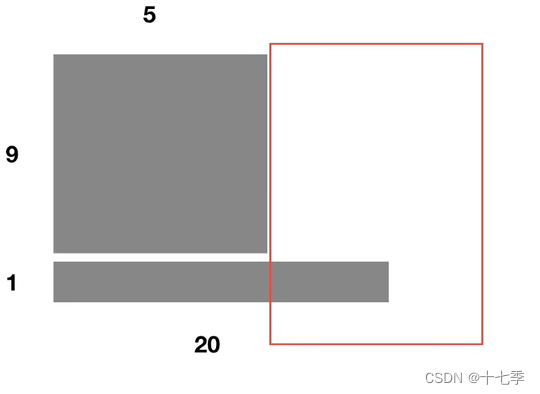
2.5.2 Layer Normal
针对同一样本的不同维度(特征)进行标准化处理,使得均值为0,方差为1。
3. Decoder
与
的组成模块大体相似,主要的不同在于
与交互层。
论文中的具有6层堆叠网络,其中每层网络有2个子层,多插入了第三个子层。
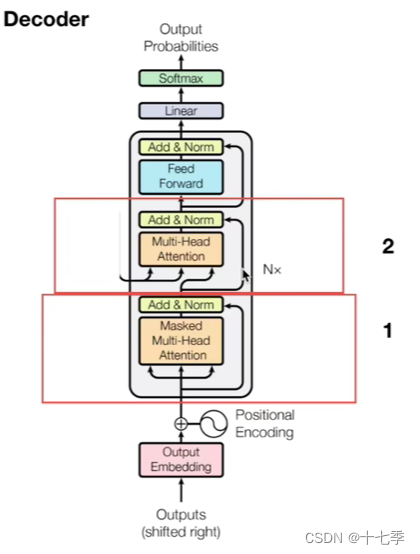
3.1 Mask
需要Mask的原因:若与Encoder一样没有Mask,则会导致预测结果偏差。因为那样子训练模型的时候后续单词是可见的,但实际预测时,未来的单词是不可知的。因此将后续的单词计入影响是不合适的。
实现Mask的方法:计算权重时,t时刻之后的值替换为很大的负数,指数变换后为0。
3.2 交互层
每个Encoder与所有的Decoder进行交互。k,v来自于Encoder本身,q来自于Decoder。这里相当于Decoder中的每个q去询问每个Encoder输出的量,并与之结合。
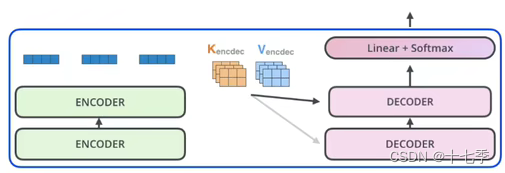
但是在实际代码训练中,一般Encoder生成q,k矩阵,Decoder生成v矩阵加权。
参考资料:
Vaswani, Ashish, et al. “Attention is All You Need.” Advances in Neural Information Processing Systems (NIPS), 2017.
Transformer论文逐段精读【论文精读】_哔哩哔哩_bilibili
Transformer从零详细解读(可能是你见过最通俗易懂的讲解)_哔哩哔哩_bilibili
超强动画,一步一步深入浅出解释Transformer原理!_哔哩哔哩_bilibili
相关文章:

简单易懂的Transformer学习笔记
1. 整体概述 2. Encoder 2.1 Embedding 2.2 位置编码 2.2.1 为什么需要位置编码 2.2.2 位置编码公式 2.2.3 为什么位置编码可行 2.3 注意力机制 2.3.1 基本注意力机制 2.3.2 在Trm中是如何操作的 2.3.3 多头注意力机制 2.4 残差网络 2.5 Batch Normal & Layer Narmal 2.…...

C语言经典小游戏之三子棋(超详解释+源码)
“纵有疾风来,人生不言弃,风乍起,合当奋意向此生。” 今天我们一起来学习一下三子棋小游戏用C语言怎么写出来? 三子棋小游戏 1.游戏规则介绍2.游戏准备3.游戏的实现3.1生成菜单3.2游戏的具体实现3.2.1初始化棋盘3.2.2打印棋盘3.2…...
宝塔Linux面板点击SSL闪退打不开?怎么解决?
宝塔Linux面板点击SSL证书闪退如何解决?旧版本的宝塔Linux面板确实存在这种情况,如何解决?升级你的宝塔Linux面板即可。新手站长分享宝塔面板SSL闪退的解决方法: 宝塔面板点击SSL证书闪退解决方法 问题:宝塔Linux面板…...

Problem: 6953. 判断是否能拆分数组
Problem: 6953. 判断是否能拆分数组 文章目录 思路解题方法复杂度Code 思路 针对题目中的以下目标,可以转换寻求数组中是否存在前后两个元素之和>m的情况,如果存在则返回ture,如果不存在则返回false。能这样转换的原因是,如果…...

MobiSys 2023 | 多用户心跳监测的双重成形声学感知
注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI, SenSys, Ubicomp; JSAC, 雷达学报 等)。本次介绍的论文是:<<MobiSys’23,Multi-User A…...
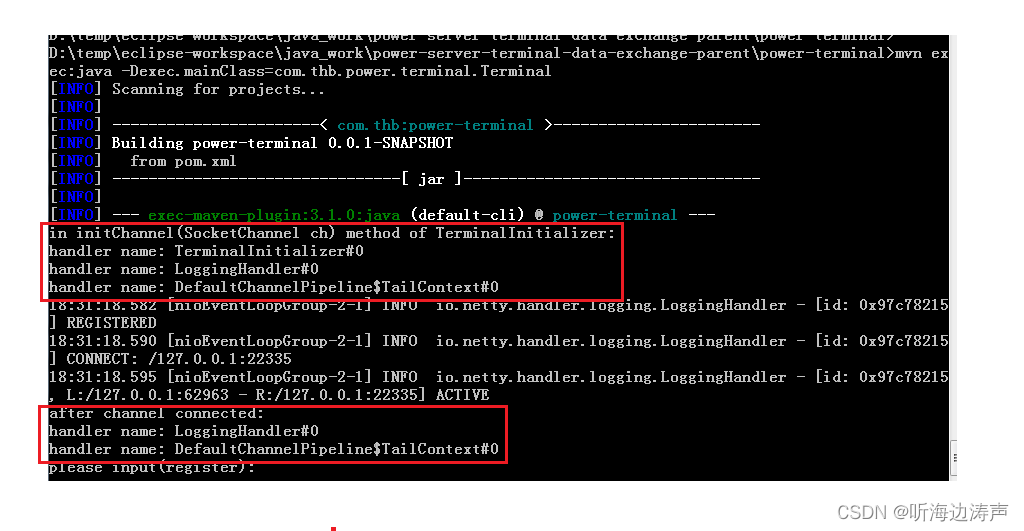
Netty:ChannelInitializer添加到ChannelPipeline完成任务以后会自动删除自己
说明 io.netty.channel.ChannelInitializer是一个特殊的ChannelInboundHandler。它的主要作用是向 Channel对应的ChannelPipeline中增加ChannelHandler。执行完ChannelInitializer的initChannel(C ch)函数以后,ChannelInitializer就会从ChannelPipeline自动删除自己…...

【VUE】项目本地开启https访问模式(vite4)
在实际开发中,有时候需要项目以https形式进行页面访问/调试,下面介绍下非vue-cli创建的vue项目如何开启https 环境 vue: ^3.2.47vite: ^4.1.4 根据官方文档:开发服务器选项 | Vite 官方中文文档 ps:首次操作,不要被类…...

【状态估计】一维粒子滤波研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

设计模式-迭代器模式在Java中使用示例
场景 为开发一套销售管理系统,在对该系统进行分析和设计时,发现经常需要对系统中的商品数据、客户数据等进行遍历, 为了复用这些遍历代码,开发人员设计了一个抽象的数据集合类AbstractObjectList,而将存储商品和客户…...

Maven入职学习
一、什么是Maven? 概念: Maven是一种框架。它可以用作依赖管理工具、构建工具。 它可以管理jar包的规模、jar包的来源、jar包之间的依赖关系。 它的用途就是管理规模庞大的jar包,脱离IDE环境执行构建操作。 具体使用: 工作机…...
【多音音频测试信号】具有指定采样率和样本数的多音信号,生成多音信号的相位降低波峰因数研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
LeetCode150道面试经典题-删除有序数组中的重复项(简单)
1.题目 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,…...

人大金仓数据库Docker部署
docker 搭建 yum -y install yum-utilsyum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.reposystemctl start docker.servicesystemctl enable docker.servicesystemctl status docker.service 配置Docker cd /etc/docker/ vi da…...

Leetcode-每日一题【剑指 Offer 07. 重建二叉树】
题目 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,20,7]Output: [3,9,20,null,null,15,7] 示例 2: Input: preo…...

Shell编程快速入门
Shell编程快速入门 脚本格式要求 脚本以#!/bin/bash开头脚本需要有可执行权限 脚本的常用执行方式 方式1:输入脚本的绝对路径或相对路径方式2:sh脚本 Shell的变量 Shell变量介绍 Linux Shell中的变量分为系统变量和用户自定义变量 系统变量&#…...

wpf 3d 坐标系和基本三角形复习
wpf 3d 坐标系的描述见此, WPF 3d坐标系和基本三角形_wpf 坐标系_bcbobo21cn的博客-CSDN博客 X轴正向向右,Y轴正向向上;Z轴,正向是从屏幕里边出来,负向是往屏幕里边去;坐标原点是在呈现区域的中心&#x…...

如何安全变更亚马逊收款账户?
有太多的卖家想知道如何安全变更亚马逊收款账户,因为更改了第三方收款账户可能会导致二次视频认证或者增强视频。真的是这样吗? 其实不推荐亚马逊店铺正常运营之后去变更信用卡,收款账户等重要资料的,因为玩黑科技的卖家也真的多…...

大数据面试题:Hadoop中的几个进程和作用
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)启动Hadoop,都会有什么进程 参考答案: 1)NameNode:Master…...

题解:ABC276D - Divide by 2 or 3
题解:ABC276D - Divide by 2 or 3 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:入门。 思维难度:入门。 调码难度:入门。 综合评价:极简。 算法 数论。 思路 由大脑可知&#x…...

后台管理系统
1.1 项目概述 简易后台管理系统是一个基于Vue3ElemrntPlus的后台管理系统,提供了用户登录、记住密码、数据的增删改查、分页、错误信息提示等功能,旨在协助管理员对特定数据进行管理和操作。 没有后台对接,数据源为假数据。 全部代码已上传G…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
