【状态估计】一维粒子滤波研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
一维粒子滤波(1D Particle Filter)是一种基于粒子的滤波算法,用于估计一个系统中的状态变量。下面是对一维粒子滤波的概述:
1. 系统建模:首先,需要建立系统的状态空间模型。一维粒子滤波通常描述为一个动态系统,其中状态变量在时间步中随机演化。这可以通过一个状态转移函数来建模,通常假设系统的演化是非线性的。
2. 粒子表示:在一维粒子滤波中,使用一组粒子来表示对状态变量的估计。每个粒子都是一个状态假设,对系统的可能状态进行采样,可以使用随机数生成方法来生成粒子。
3. 重采样:随着时间推移和系统演化,粒子的权重会发生变化。在一维粒子滤波中,需要对粒子进行重采样,以根据它们的权重重新分配粒子的数量。重采样的目的是为了保留那些具有较高权重的粒子,去除那些权重较低的粒子。
4. 状态更新:根据测量观测值,需要对粒子进行状态更新。这是通过计算每个粒子的观测概率来实现的。观测概率度量了一个粒子与测量值之间的一致性,可以使用测量模型来计算。
5. 状态估计:根据粒子的权重,可以计算系统状态的估计值。一种常见的方法是使用粒子的加权平均值作为状态的估计,其中权重反映了粒子的可能性。
一维粒子滤波是一种基于贝叶斯滤波原理的非参数滤波方法,可以用于状态估计和跟踪问题。它适用于非线性系统和非高斯噪声的情况,并且能够处理多模态分布。然而,粒子滤波的效率和精度受到粒子数目的影响,过多的粒子会导致计算复杂度增加,而过少的粒子会引入估计误差。
以上是对一维粒子滤波的概述,涉及系统建模、粒子表示、重采样、状态更新和状态估计等关键步骤。具体的应用案例和算法细节可以根据实际问题进行调整和扩展。
📚2 运行结果
在命令框内按一个键才能逐步完成模拟。以蓝色显示移动前的粒子(带直方图)、用红线移动后的实际位置、用洋红色线显示的测量值、运动模型向前传播并根据测量值加权的粒子(以黑色显示),以红色显示重采样粒子(带直方图)
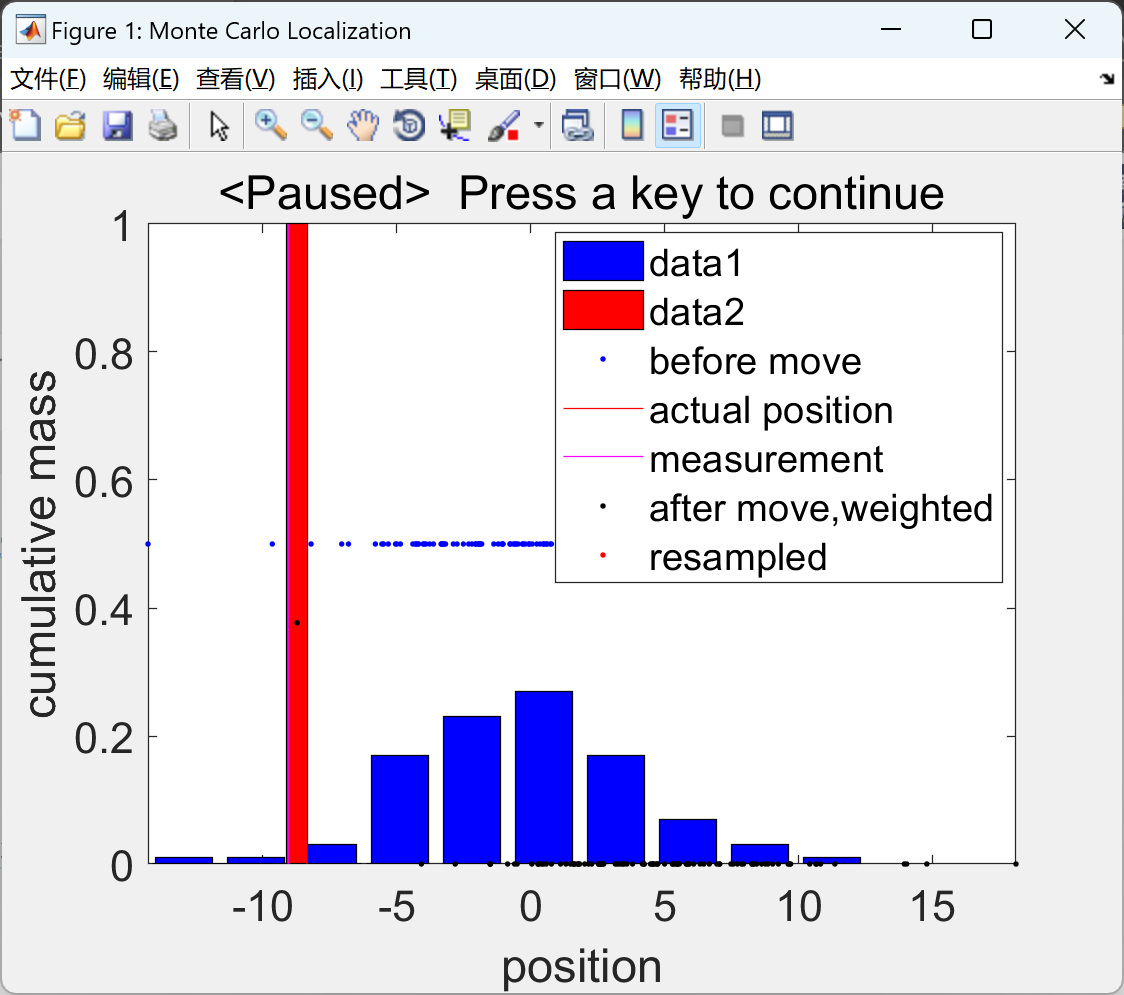
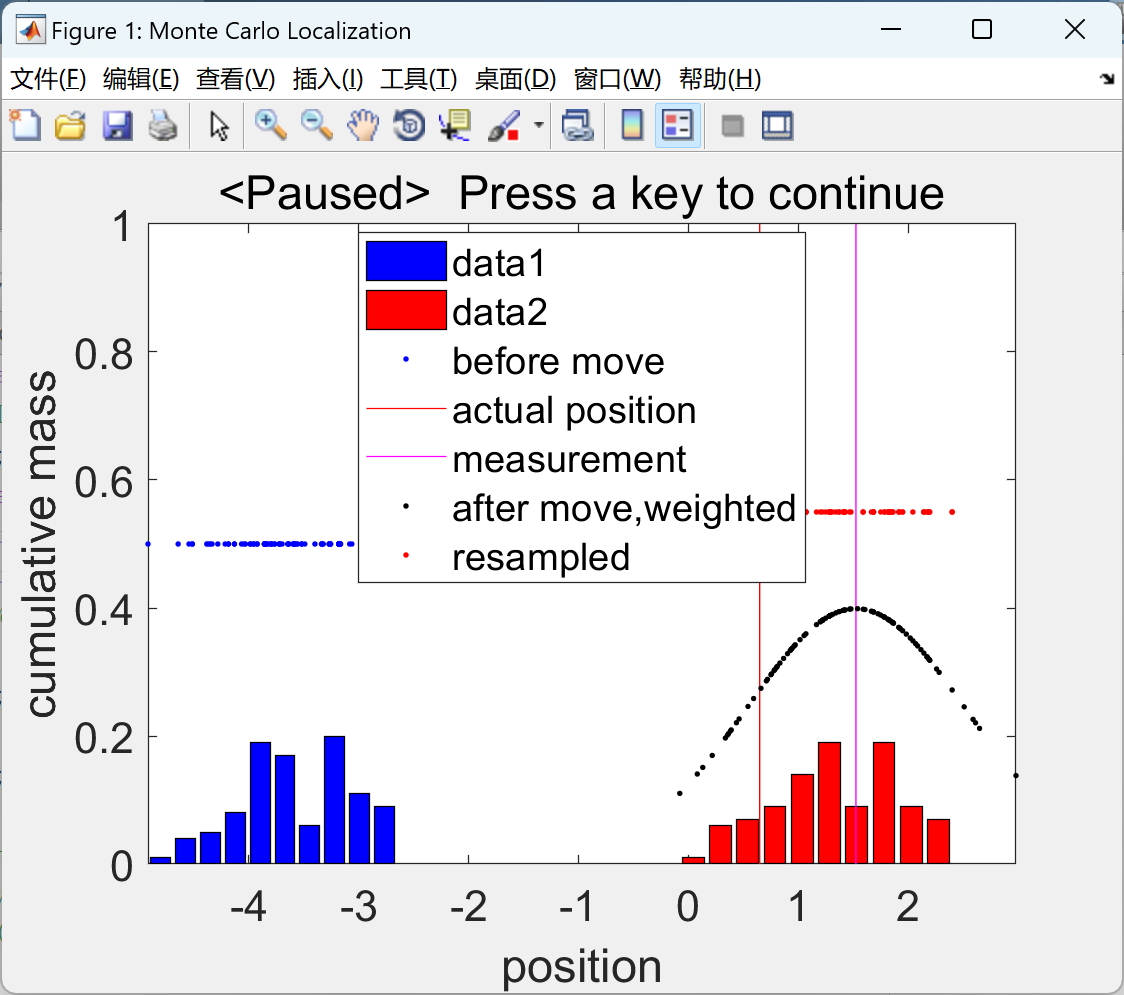

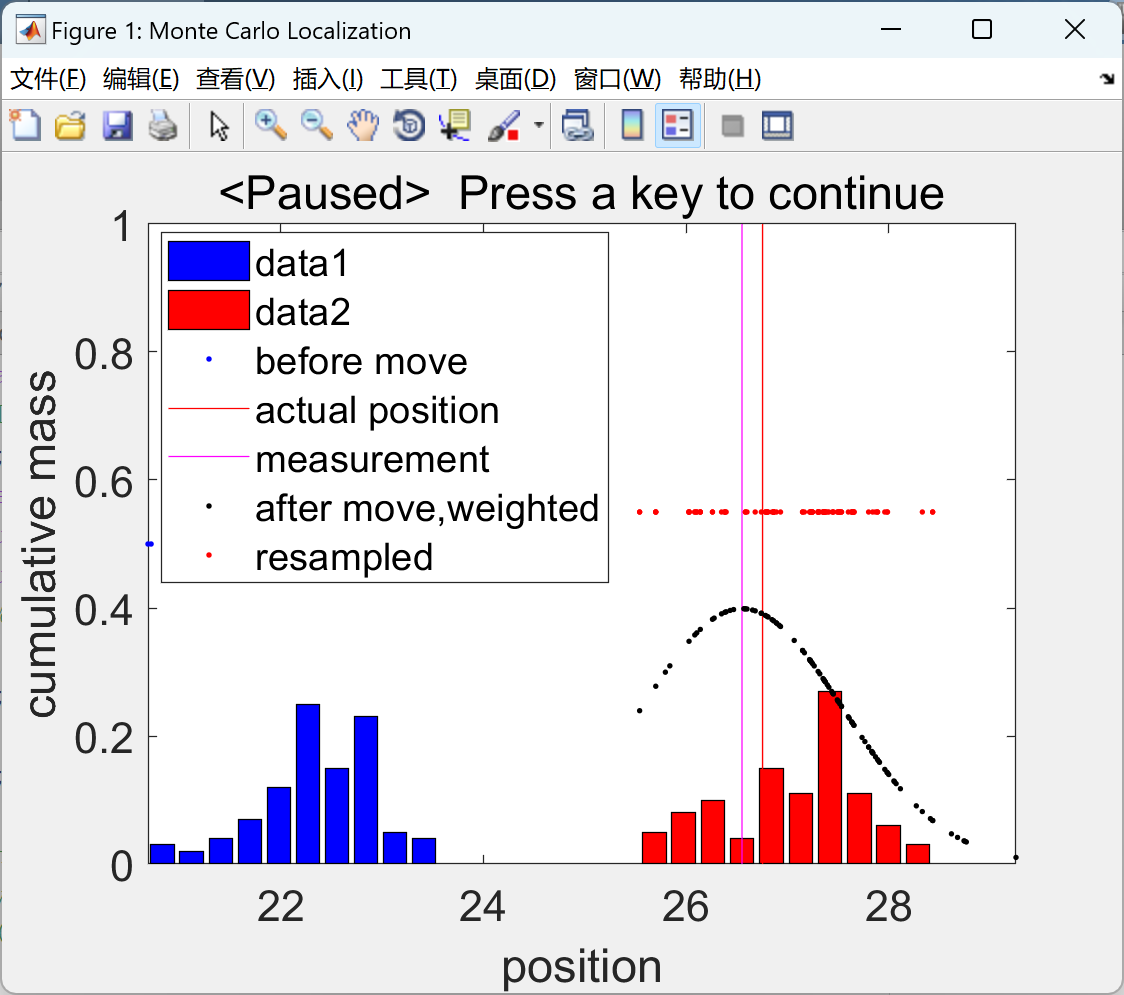

部分代码:
%%% PLOT SETTINGS %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f1 = figure;
set(f1,'name', 'Monte Carlo Localization')
set(0,'defaultaxesfontsize',16);
set(0,'defaulttextfontsize',16);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
SIGmeas = 1; %standard deviation of measurement noise
SIGproc = 0.5; %standard deviation of process noise
SIGinit = 4; %standard deviation of initial position
M = 100; %number of particles (the more, the better the particle
%Probability Mass Function (PMF) matches the true Probability Distribution
% Function (PDF).
CHI = [SIGinit*randn(M,1), ones(M,1)/M]; %array of particles and associated weights
xACTt = SIGinit*randn(1); %true position of the robot (unknown to particles)
ut = 5; %control input (constant motion in x-direction)
max_moves = 10;
for mv = 1:max_moves
% move ACTUAL robot
xACTt = sample_motion_model(ut, xACTt, SIGproc);
%take measurement
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
1. 杨琛, 孟翔宇, 李绪连. (2017). 一维离散曲线上的粒子滤波算法. 计算机科学, 44(11), 261-263.
2. 吉宇峰, 赵孜辰, 李燕. (2016). 一维非线性系统的粒子滤波算法研究. 计算机科学与探索, 10(7), 767-775.
3. 孙增茹, 吴琳, 张良康. (2015). 基于一维粒子滤波算法的离散状态系统状态估计. 控制工程, 22(5), 826-829.
4. 赵凯, 张余波, 郑劲松等. (2016). 基于动力系统的一维离散状态粒子滤波算法研究. 电子与信息学报, 38(9), 2359-2366.
🌈4 Matlab代码实现
相关文章:

【状态估计】一维粒子滤波研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

设计模式-迭代器模式在Java中使用示例
场景 为开发一套销售管理系统,在对该系统进行分析和设计时,发现经常需要对系统中的商品数据、客户数据等进行遍历, 为了复用这些遍历代码,开发人员设计了一个抽象的数据集合类AbstractObjectList,而将存储商品和客户…...

Maven入职学习
一、什么是Maven? 概念: Maven是一种框架。它可以用作依赖管理工具、构建工具。 它可以管理jar包的规模、jar包的来源、jar包之间的依赖关系。 它的用途就是管理规模庞大的jar包,脱离IDE环境执行构建操作。 具体使用: 工作机…...
【多音音频测试信号】具有指定采样率和样本数的多音信号,生成多音信号的相位降低波峰因数研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
LeetCode150道面试经典题-删除有序数组中的重复项(简单)
1.题目 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,…...

人大金仓数据库Docker部署
docker 搭建 yum -y install yum-utilsyum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.reposystemctl start docker.servicesystemctl enable docker.servicesystemctl status docker.service 配置Docker cd /etc/docker/ vi da…...

Leetcode-每日一题【剑指 Offer 07. 重建二叉树】
题目 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,20,7]Output: [3,9,20,null,null,15,7] 示例 2: Input: preo…...

Shell编程快速入门
Shell编程快速入门 脚本格式要求 脚本以#!/bin/bash开头脚本需要有可执行权限 脚本的常用执行方式 方式1:输入脚本的绝对路径或相对路径方式2:sh脚本 Shell的变量 Shell变量介绍 Linux Shell中的变量分为系统变量和用户自定义变量 系统变量&#…...

wpf 3d 坐标系和基本三角形复习
wpf 3d 坐标系的描述见此, WPF 3d坐标系和基本三角形_wpf 坐标系_bcbobo21cn的博客-CSDN博客 X轴正向向右,Y轴正向向上;Z轴,正向是从屏幕里边出来,负向是往屏幕里边去;坐标原点是在呈现区域的中心&#x…...

如何安全变更亚马逊收款账户?
有太多的卖家想知道如何安全变更亚马逊收款账户,因为更改了第三方收款账户可能会导致二次视频认证或者增强视频。真的是这样吗? 其实不推荐亚马逊店铺正常运营之后去变更信用卡,收款账户等重要资料的,因为玩黑科技的卖家也真的多…...

大数据面试题:Hadoop中的几个进程和作用
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)启动Hadoop,都会有什么进程 参考答案: 1)NameNode:Master…...

题解:ABC276D - Divide by 2 or 3
题解:ABC276D - Divide by 2 or 3 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:入门。 思维难度:入门。 调码难度:入门。 综合评价:极简。 算法 数论。 思路 由大脑可知&#x…...

后台管理系统
1.1 项目概述 简易后台管理系统是一个基于Vue3ElemrntPlus的后台管理系统,提供了用户登录、记住密码、数据的增删改查、分页、错误信息提示等功能,旨在协助管理员对特定数据进行管理和操作。 没有后台对接,数据源为假数据。 全部代码已上传G…...

C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构)
本文目录 00.BBST——平衡二叉搜索树01.AVL树02.AVL的插入2.1单旋——zig 与 zag2.2插入节点后的单旋实例2.3手玩小样例2.4双旋实例2.5小结 03.AVL的删除3.1单旋删除3.2双旋删除3.3小结 04.34重构05.综合评价AVL5.1优点5.2缺点 06.代码注意插入算法删除算法完整代码:…...
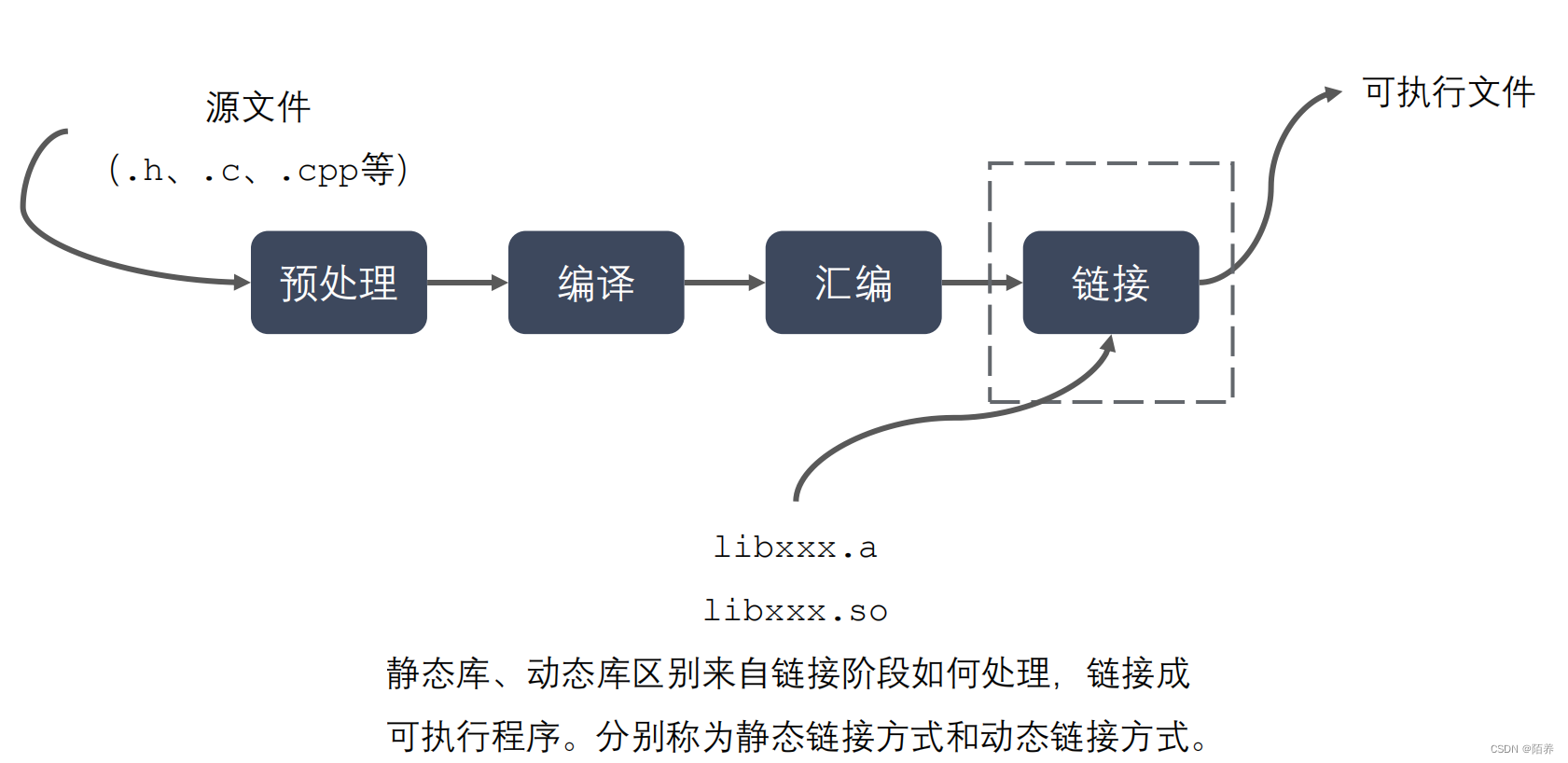
静态库和动态库
库文件 库文件是计算机上的一类文件,可以简单的把库文件看成一种代码仓库,它提供给使用者一些可以直接拿来用的变量、函数或类。 库是特殊的一种程序,编写库的程序和编写一般的程序区别不大,只是库不能单独运行。库文件有两种&a…...

用于Voronoi图构建的Fortune算法的C++实现
Voronoi图是一种在计算几何中广泛使用的数据结构,它可以用于解决最近邻搜索、路径规划等问题。在这篇文章中,我们将探讨一种用于构建Voronoi图的高效算法——Fortune算法,并提供其C实现。 一、Voronoi图简介 Voronoi图是由一组点在平面上生…...

笔记汇总 | 斯坦福 CS229 机器学习
文章目录 前言课程参考文章推荐阅读 前言 本文为斯坦福大学 CS229 机器学习课程学习笔记 本文主体部分转载自黄海广博士,文末已给出链接,大家有兴趣可以直接访问笔记首页,下载对应课程资料及作业代码 课程官网:CS229: Machine …...

git 版本管理工具 学习笔记
git 学习笔记 目录 一、git是什么 二、创建仓库 三、工作区域和文件状态 四、添加和提交文件 五、回退版本 (了解) 六、查看差异 七、删除文件 八、.gitignore文件(了解) 九、github ssh-key配置 十、本地仓库和远程仓库内…...
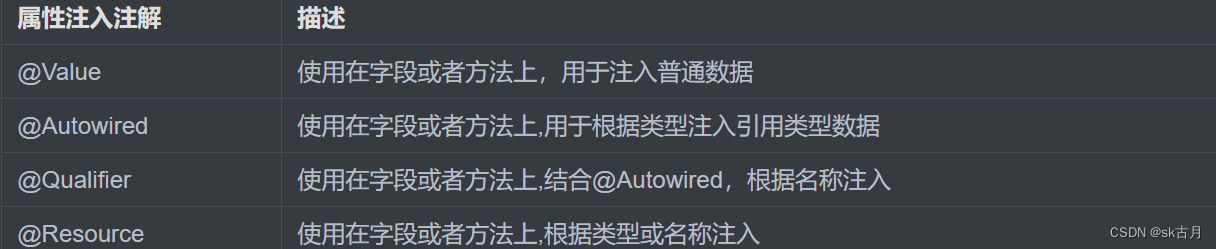
Bean基本注解开发和Bean依赖注入注解开发
目录 1.Bean基本注解开发 Component Scorelazy PostConstruct和PreDestroy RepositoryServiceController 2.Bean依赖注入注解开发 Value Autowired Qualifier Resource 扩展AutoWired 1.Bean基本注解开发 基本Bean注解,主要是使用注释的方式替代原有xml的…...
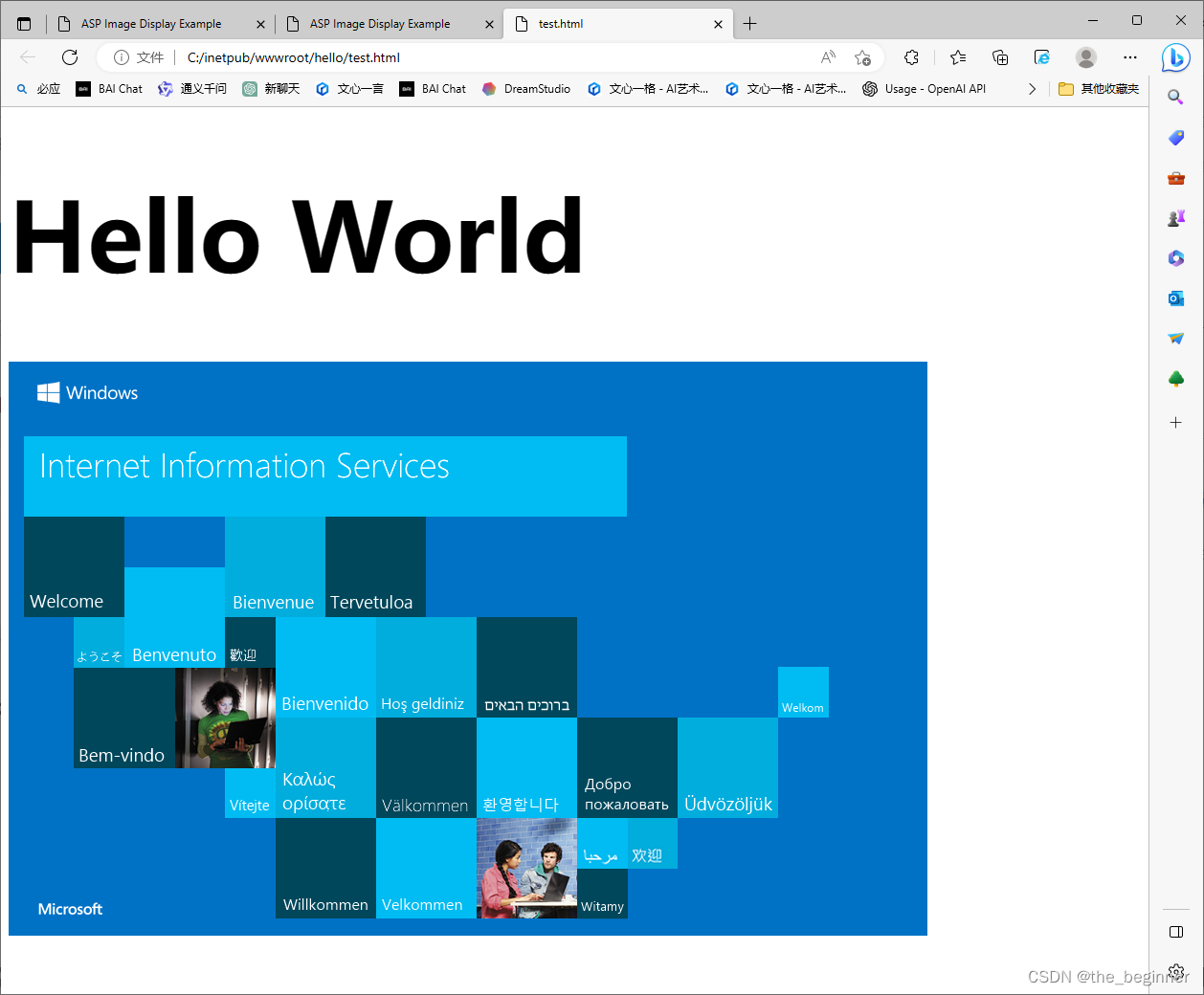
使用IIS服务器搭建一个网站
参考文章 使用IIS(Internet Information Services)服务器搭建一个网站相对来说是比较简单的。以下是基本的步骤: 安装IIS: 首先,确保你的操作系统已经安装了IIS。在大多数Windows版本中,IIS都是可选安装项…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

