二分法的应用

文章目录
- 什么是二分法🎮
- 二分查找的优先级
- 二分查找的步骤💥
- 图解演示🧩
- 代码演示🫕
- python程序实现🐈⬛
- C程序实现🐕🦺
- C++程序实现🐯
- Java程序实现🐳
- 非常规类二分查找🏡
- 查找有序列表中某数首次出现的位置🫖
什么是二分法🎮
二分法(Bisection method),即一分为二的的方法。数学的零点估计问题中:对于在区间[a,b]上连续不断且满足 f(a) * f(b) <0的函数y=f(x),通过不断地把函数f(x)的零点所在区间二等分,使区间两个端点逐步逼近零点,进而得到零点的近似值的方法。
😎当然,在我们技术人的手中,一般是用来解决有序列表中查找某个元素的问题,属于搜索方法的一种。
😵💫简单的来说,就是将答案所在的区间不断缩小为原来的 1/2,直到找到答案。
🎉类似二分法的实例
假如你和朋友在玩猜数字游戏,朋友记录一个数,规定数的范围,你来猜。你每猜一个数,朋友会告诉你这个数大了还是小了,直到你猜出正确答案为止。假如有100个数,你一个一个数猜,你最差的情况需要找100次,如果你使用二分的思想查找,每次折半,最多只需要7次即可猜出答案。
二分查找的优先级
二分查找算法的时间复杂度为O(log n),因此其优先级较高,适合在需要快速查找有序列表中的元素时使用。相比于线性查找算法的时间复杂度为O(n),二分查找算法具有更高的效率,尤其适用于数据量较大的情况。同时,二分查找算法较为简单,易于实现和理解,因此被广泛应用于各个领域的程序设计中。
二分查找的效率虽然高,但只局限于有序列表
二分查找的步骤💥
二分查找的思路是先取中间位置的值进行比较,如果该值等于目标值,则查找成功;否则,如果该值大于目标值,则在左半部分继续查找;如果该值小于目标值,则在右半部分继续查找。不断重复以上步骤,直到找到目标值或者确定目标值不存在为止。
图解演示🧩
在下面这个有序数组中查找数字3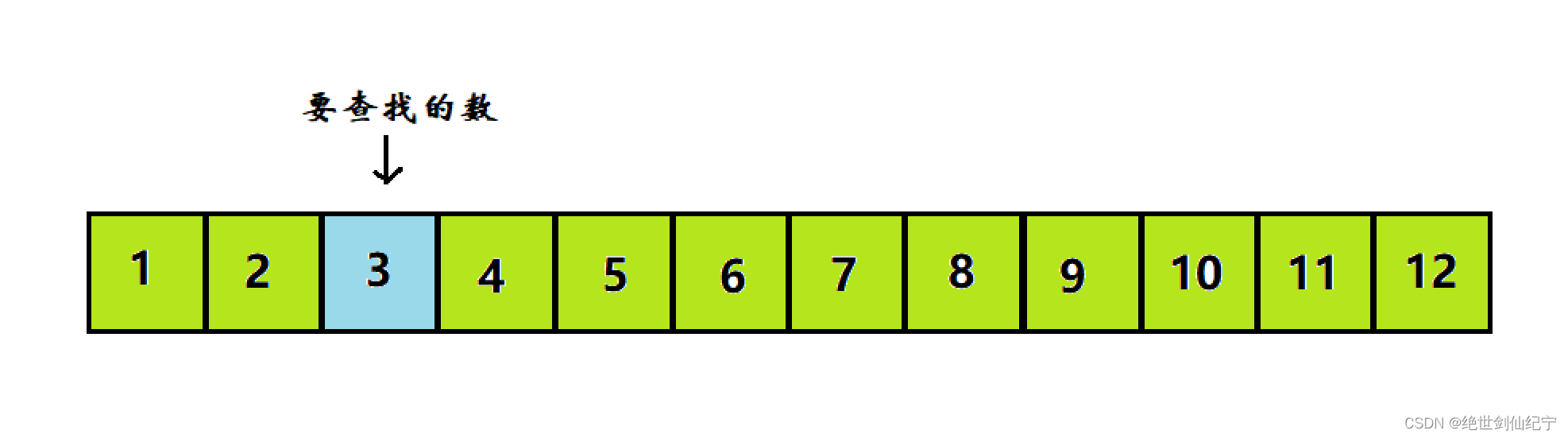
定义三个指针:left、right、mid
这三个指针都是动态的,left 为左边界的下标,right 为右边界的下标,mid=(left+right)/2

arr[mid]>3,中间值大于目标值,说明右边没有要查找的数,之后范围缩小到左边。
改变右指针right=mid-1
这里 arr[mid] 恰好等于要查找的数,二分结束。
假设要查找的数变为4,那么还需要继续查找,如图
arr[mid]<4,中间值小于目标值,说明左边没有要查找的数,范围再缩小到原来的右边
改变左指针left=mid+1

arr[mid]=4 就找到了需要查找的数
当左指针 left 大于等于右指针 right 时,二分查找结束,答案可能是找到目标值或者目标值不存在。
代码演示🫕
其中,arr为有序列表,target为需要查找的元素,最终未找到就返回 -1
python程序实现🐈⬛
def binary_search(arr, target):left, right = 0, len(arr) - 1while left <= right:mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:left = mid + 1else:right = mid - 1return -1定义一个函数binary_search,该函数接受两个参数:一个有序数组 arr 和要查找的目标元素 target
C程序实现🐕🦺
#include <stdio.h>// 二分查找函数
int binary_search(int arr[], int left, int right, int target){while (left <= right) // 当left>right时停止查找{int mid = (left + right) / 2; // 计算中间位置if (arr[mid] == target) // 找到目标值{return mid;}else if (arr[mid] < target) // 目标值在右半部分{left = mid + 1;}else // 目标值在左半部分{right = mid - 1;}}return -1; // 没有找到目标值
}int main()
{int arr[] = {1, 3, 5, 7, 9, 11}; // 有序数组int n = sizeof(arr) / sizeof(arr[0]); // 数组长度int target = 5; int index = binary_search(arr, 0, n - 1, target); // 进行二分查找if (index == -1){printf("目标值不存在\n");}else{printf("目标值在数组中的下标为:%d\n", index);}return 0;
}
自己定义一个函数binary_search,接收数组、数组的左右边界下标(或数组元素个数),以及要查找的元素
C++程序实现🐯
#include <iostream>
using namespace std;int binarySearch(int arr[], int l, int r, int x) {if (r >= l) {int mid = l + (r - l) / 2;if (arr[mid] == x) {return mid;}if (arr[mid] > x) {return binarySearch(arr, l, mid - 1, x);}return binarySearch(arr, mid + 1, r, x);}return -1;
}int main() {int arr[] = { 2, 4, 6, 8, 10 };int n = sizeof(arr) / sizeof(arr[0]);int x = 8;int result = binarySearch(arr, 0, n - 1, x);if (result == -1) {cout << "Element not found" << endl;}else {cout << "Element found at index " << result << endl;}return 0;
}函数binarySearch为二分查找函数,该函数接受一个整数数组,数组的左右边界以及要查找的元素
Java程序实现🐳
public class BinarySearch {int binarySearch(int arr[], int l, int r, int x) {if (r >= l) {int mid = l + (r - l) / 2;if (arr[mid] == x) {return mid;}if (arr[mid] > x) {return binarySearch(arr, l, mid - 1, x);}return binarySearch(arr, mid + 1, r, x);}return -1;}public static void main(String args[]) {BinarySearch bs = new BinarySearch();int arr[] = { 2, 4, 6, 8, 10 };int n = arr.length;int x = 8;int result = bs.binarySearch(arr, 0, n - 1, x);if (result == -1) {System.out.println("Element not found");}else {System.out.println("Element found at index " + result);}}
}在此示例中定义了一个类BinarySearch,其中包含一个递归函数binarySearch,该函数接受一个整数数组,数组的左右边界以及要查找的元素。
非常规类二分查找🏡
查找有序列表中某数首次出现的位置🫖
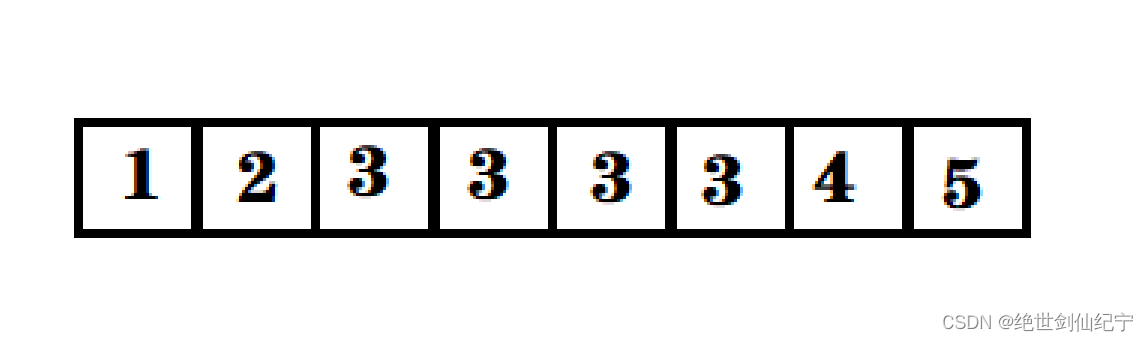
如下图中,找到3首次出现的位置(左边界),不难。但要以时间复杂度为 log(N)找到,就要采用二分查找了。
C程序代码
int Find_Edges(int*nums,int len,double k)
{int left=0,right=len-1;while(left<=right){int mid=(left+right)/2;if(nums[mid]<k)left=mid+1;else if(nums[mid]>k)right=mid-1;}return left;
}int GetNumberOfK(int* nums, int numsLen, int k ) {return Find_Edges(nums,numsLen,k-0,5);
}
上面这段代码将参数 3-0.5 传上去,就可以求出3的左边界,因为传上去的是浮点数,那肯定是找不到的,只能找到距离最近的向上取整的可以找到的数,因为整数除法是向下取整的,所以,mid的值一定是小于等于 (left+right)/2的,所以一定会在 left 位置结束二分查找。
同样,将参数 3+0.5 传上去,就可以求出3的右边界,进而求出这个数组中一共有多少个3,进而解决这篇博客中最后一题C语言笔试训练。
相关文章:

二分法的应用
文章目录 什么是二分法🎮二分查找的优先级二分查找的步骤💥图解演示🧩 代码演示🫕python程序实现🐈⬛C程序实现🐕🦺C程序实现🐯Java程序实现🐳 非常规类二分查找&…...

ChatGPT在大规模数据处理和信息管理中的应用如何?
ChatGPT作为一种强大的自然语言处理模型,在大规模数据处理和信息管理领域有着广泛的应用潜力。它可以利用其文本生成、文本理解和问答等能力,为数据分析、信息提取、知识管理等任务提供智能化的解决方案。以下将详细介绍ChatGPT在大规模数据处理和信息管…...
【算法篇C++实现】五大常规算法
文章目录 🚀一、分治法⛳(一)算法思想⛳(二)相关代码 🚀二、动态规划算法⛳(一)算法思想⛳(二)相关代码 🚀三、回溯算法⛳(一…...

MySQL和钉钉单据接口对接
MySQL和钉钉单据接口对接 数据源系统:钉钉 钉钉(DingTalk)是阿里巴巴集团打造的企业级智能移动办公平台,是数字经济时代的企业组织协同办公和应用开发平台。钉钉将IM即时沟通、钉钉文档、钉闪会、钉盘、Teambition、OA审批、智能人事、钉工牌…...

layui的基本使用-日期控件的业务场景使用入门实战案例一
效果镇楼; 1 前端UI层面; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport&…...
【2.1】Java微服务:详解Hystrix
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: Java微服务 ✨特色专栏: 知识分享 &am…...
Apache2.4源码安装与配置
环境准备 openssl-devel pcre-devel expat-devel libtool gcc libxml2-devel 这些包要提前安装,否则httpd编译安装时候会报错 下载源码、解压缩、软连接 1、wget下载[rootnode01 ~]# wget https://downloads.apache.org/httpd/httpd-2.4.57.tar.gz --2023-07-20 …...
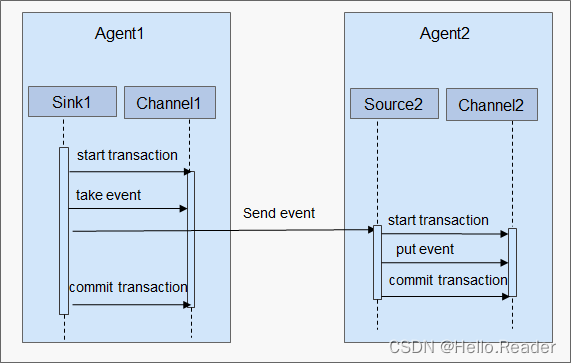
Flume原理剖析
一、介绍 Flume是一个高可用、高可靠,分布式的海量日志采集、聚合和传输的系统。Flume支持在日志系统中定制各类数据发送方,用于收集数据;同时,Flume提供对数据进行简单处理,并写到各种数据接受方(可定制&…...
)
【leetcode】202. 快乐数(easy)
编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果这个过程 结果为 1,…...
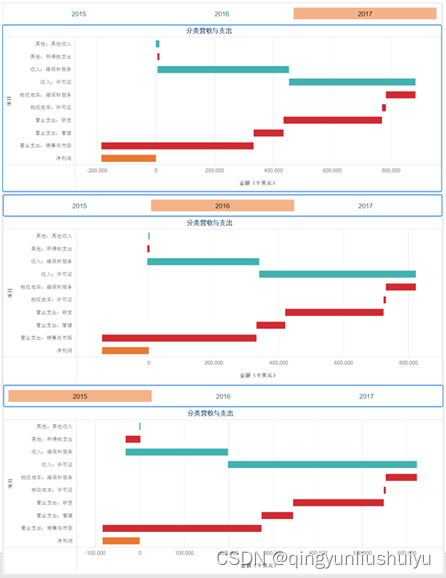
如何用瀑布图分析公司年报
原创: MicroStrategy微策略中国 , Jiping Sun 微策略企业级数据分析与移动应用9月21日2018年 摘要:利用达析报告开箱即用的瀑布图来展示各个度量值如何增加或减少。下载MicroStrategy Desktop 10.11以上版本,自己动手创建瀑布图。 瀑布图是由…...
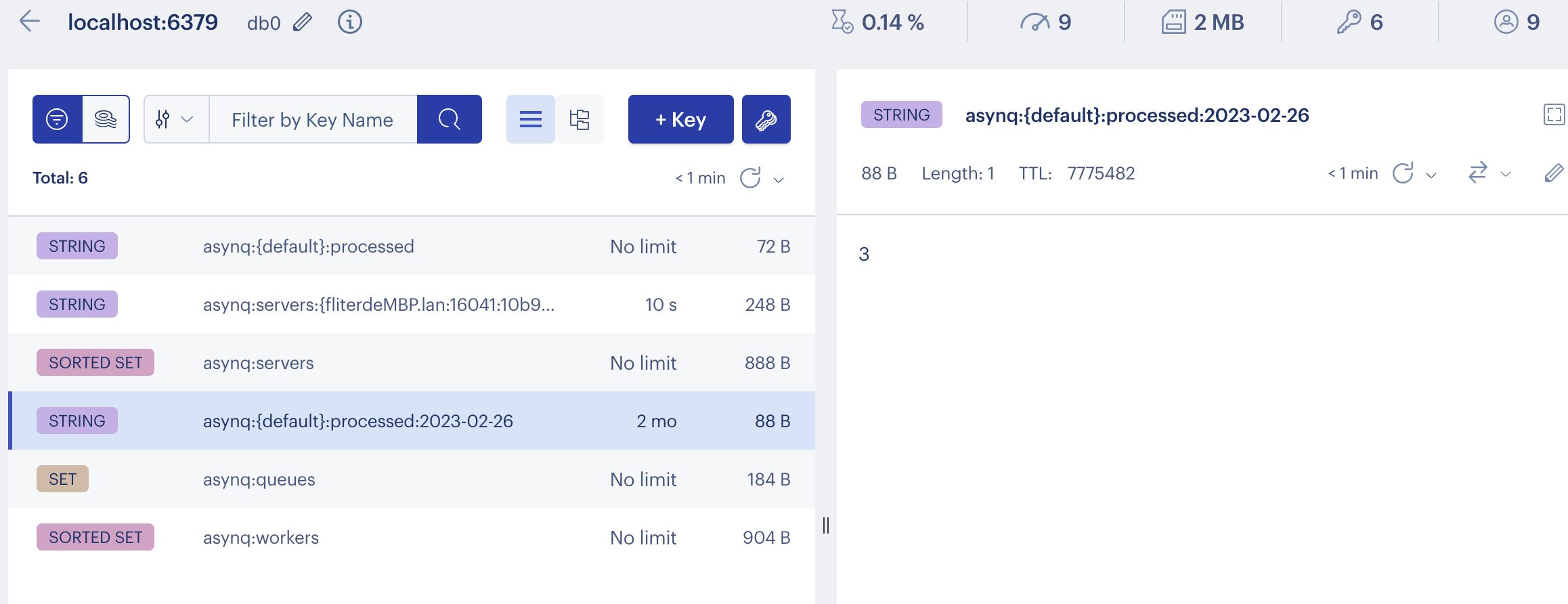
Asynq: 基于Redis实现的Go生态分布式任务队列和异步处理库
Asynq[1]是一个Go实现的分布式任务队列和异步处理库,基于redis,类似Ruby的sidekiq[2]和Python的celery[3]。Go生态类似的还有machinery[4]和goworker 同时提供一个WebUI asynqmon[5],可以源码形式安装或使用Docker image, 还可以和Prometheus…...

保证率计算公式 正态分布
在正态分布中,如果我们要计算一个给定区间内的保证率,可以使用下面的计算公式: 找到给定保证率对应的标准正态分布的z值。可以使用标准正态分布表或计算器进行查询。例如,对于95%的保证率,对应的z值为1.96。 使用z值和…...
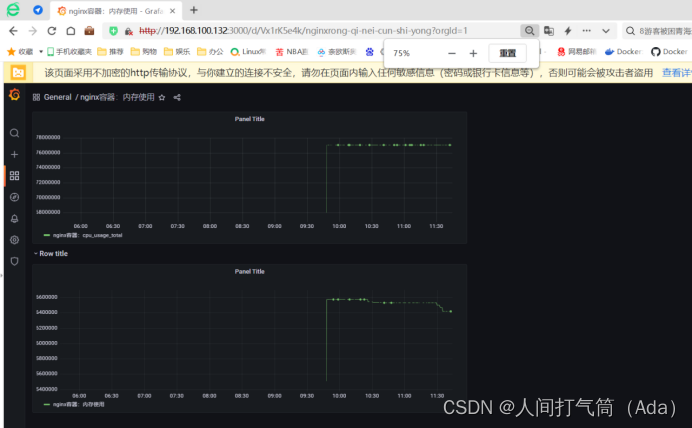
docker容器监控:Cadvisor+InfluxDB+Grafana的安装部署
目录 CadvisorInfluxDBGrafan安装部署 1、安装docker-ce 2、阿里云镜像加速器 3、下载组件镜像 4、创建自定义网络 5、创建influxdb容器 6、创建Cadvisor 容器 7、查看Cadvisor 容器: (1)准备测试镜像 (2)通…...

论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR
论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR https://arxiv.org/pdf/2210.15016.pdf概览模型转换TranslationCanonicalizeLoweringLayerGroup BufferizationCalibration QuantizationCorrectness Check相关资料 https://arxiv.org/pdf/2210.15016.pdf 本文将对TPU…...
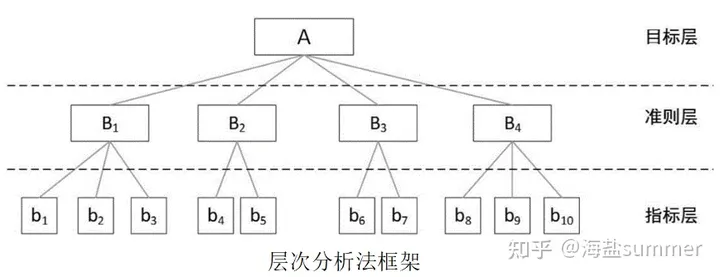
基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升
查看原文>>>基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升 目录 专题一、生态环评报告编制规范 专题二、土地利用图 专题三、植被类型及植被覆盖度图 专题四、物种适宜生境分布图 专题五、生物多样性测定 专题六…...

NGZORRO:动态表单/模型驱动 的相关问题
官网的demo的[nzFor]"control.controlInstance",似乎是靠[formControlName]"control.controlInstance"来关联的。 <form nz-form [formGroup]"validateForm" (ngSubmit)"submitForm()"><nz-form-item *ngFor&quo…...

第十七次CCF计算机软件能力认证
第一题:小明种苹果 n , m map(int , input().split()) t , k , p 0 , 0 , -1 for _ in range(n):l list(map(int , input().split()))t sum(l)x -sum(l[i] for i in range(1 , len(l)))if x > p:p xk _ 1 print(t , k , p) 第二题:小明种苹…...

ApplicationContext在Spring Boot中是如何创建的?
一、ApplicationContext在Spring Boot中是如何创建的? 1. SpringApplication ApplicationContextFactory有三个实现类,分别是AnnotationConfigReactiveWebServerApplicationContext.Factory、AnnotationConfigServletWebServerApplicationContext.Facto…...
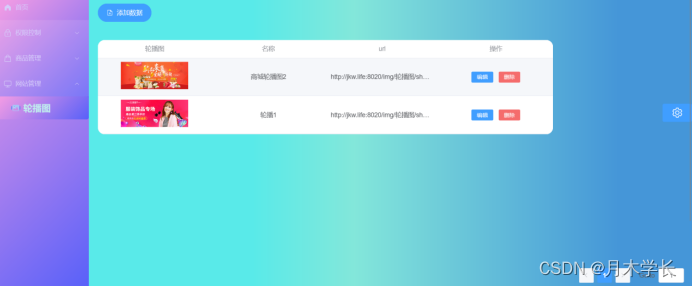
后端开发7.轮播图模块【mongdb开发】
概述 轮播图模块数据库采用mongdb开发 效果图 数据库设计 创建数据库 use sc; 添加数据 db.banner.insertMany([ {bannerId:"1",bannerName:"商城轮播图1",bannerUrl:"http://xx:8020/img/轮播图/shop1.png"}, {bannerId:"2"…...

Linux常用命令(一):创建文件目录
一、touch: 1、作用: 1). 改变已有文件的时间戳属性,修改文件时间戳时,用户必须的文件的属主,或者拥有写文件的权限 2). 创建新的空文件 2、语法: touch [option] 文件名 ,后面可跟多个文件名3、示例 …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
