【CSS】CSS 布局——常规流布局
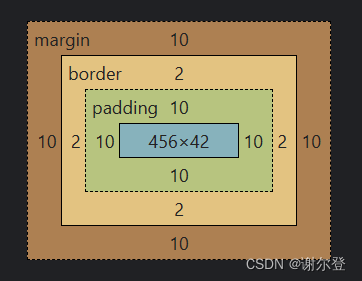
<h1>基础文档流</h1><p>我是一个基本的块级元素。我的相邻块级元素在我的下方另起一行。</p><p>默认情况下,我们会占据父元素 100%的宽度,并且我们的高度与我们的子元素内容一样高。我们的总宽度和高度是我们的内容+ 内边距 + 边框宽度/高度。
</p><p>我们以我们的外边距分隔。由于外边距折叠,我们以其中一个外边距的宽度(如果两个的外边距不相同,以更大的为准)分隔,而不是两个。
</p><p>如果在同一行上足够的空间,行级元素(如<span>这个</span>和<span>这个</span>),那么它们将与相邻的文本节点将会一起放置在同一行上。如果行级元素溢出,<span>那么它们将会换行,就像这个包含文本的行级元素一样</span>,或者如果没有足够的空间,那么它们将会换到新的一行,就像这个图片一样:<img src="long.jpg" alt="snippet of cloth" />
</p>body {width: 500px;margin: 0 auto;
}p {background: rgba(255, 84, 104, 0.3);border: 2px solid rgb(255, 84, 104);padding: 10px;margin: 10px;
}span {background: white;border: 1px solid black;
}
相关文章:

【CSS】CSS 布局——常规流布局
<h1>基础文档流</h1><p>我是一个基本的块级元素。我的相邻块级元素在我的下方另起一行。</p><p>默认情况下,我们会占据父元素 100%的宽度,并且我们的高度与我们的子元素内容一样高。我们的总宽度和高度是我们的内容 内边距…...

flutter开发实战-实现左右来回移动的按钮引导动画效果
flutter开发实战-实现左右来回移动的按钮引导动画效果 最近开发过程中需要实现左右来回移动的按钮引导动画效果 一、动画 AnimationController用来控制一个或者多个动画的正向、反向、停止等相关动画操作。在默认情况下AnimationController是按照线性进行动画播放的。Animati…...
ROS实现自定义信息以及使用
常见的消息包 消息包定义一般如下👇 (1)创建包和依赖项 (2)在新建的qq_msgs的包新建msgs的文件夹,在该文件夹里面新建Carry.msg类型的文件。 其实,Carry.msg就是你自己定义的消息类型&am…...

初始C语言——详细讲解操作符以及操作符的易错点
系列文章目录 第一章 “C“浒传——初识C语言(更适合初学者体质哦!) 第二章 详细认识分支语句和循环语句以及他们的易错点 第三章 初阶C语言——特别详细地介绍函数 第四章 初始C语言——详细地讲解数组的内容以及易错点 第五章 初始C语言—…...

论文写作常用词句积累
X 连接词 表目的To this end/Toward that endto do soto this aimso as toTo tackle these issuesfor the sake ofaiming to do表转折howeverNevertheless表递进moreverFurthermore表对比on the other hand/On the contraryAlternativelyas in the case ofwhereas表顺序in a f…...

伺服系统::编码器
一、主要分类 二、组成与原理 光电编码器 磁编码器:N-->磁感元件(0);S-->磁感元件(1)》脉冲 增量编码器的分辨率、倍频与细分技术 (99 封私信 / 81 条消息) 编码器有什么分类? - 知乎 (z…...
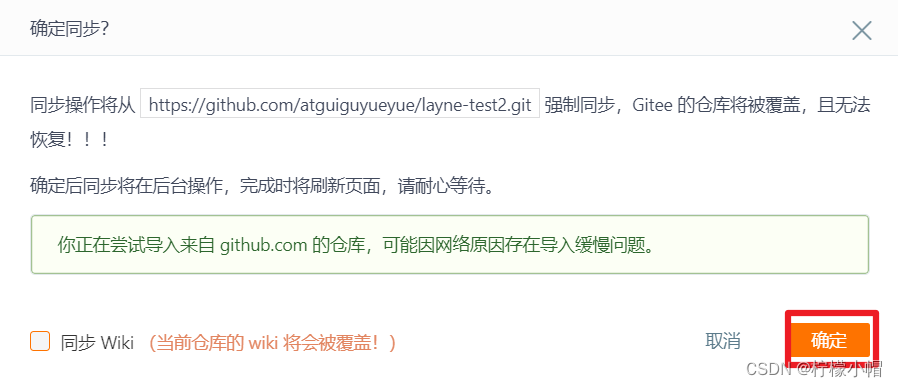
Git全栈体系(五)
第八章 IDEA 集成 GitHub 一、设置 GitHub 账号 如果出现 401 等情况连接不上的,是因为网络原因,可以使用以下方式连接: 然后去 GitHub 账户上设置 token。 点击生成 token。 复制红框中的字符串到 idea 中。 点击登录。 二、分享工程…...
spring-boot webservice的例子
webservice发布服务 源码下载地址 spring-boot-webservice例子资源-CSDN文库 webservice cilent调用 源码下载地址 spring-boot-clintwebservice调用服务的例子资源-CSDN文库...

第八章 SpringBoot @ConfigurationProperties配置绑定
原始做法:读取到文件内容,再进行bean的绑定 public static void readProperties(String propertiesPath) throws IOException {Properties pps new Properties();pps.load(MainApplication.class.getClassLoader().getResourceAsStream("applicat…...

【SpringBoot】88、SpringBoot中使用Undertow替代Tomcat容器
SpringBoot 中我们既可以使用 Tomcat 作为 Http 服务,也可以用 Undertow 来代替。Undertow 在高并发业务场景中,性能优于 Tomcat。所以,如果我们的系统是高并发请求,不妨使用一下 Undertow,你会发现你的系统性能会得到很大的提升。 1、Tomcat 介绍 Tomcat是一个开源的Ja…...

java8 求和
1.BigDecimal求和 对象字段求和 List<Car> listnew ArrayList<>(); BigDecimal sumOfBigDecimals list.stream().filter(Objects::nonNull).filter(c -> c.getMiles() ! null).map(Car::getMiles).reduce(BigDecimal.ZERO, BigDecimal::add);BigDecimal集合求…...
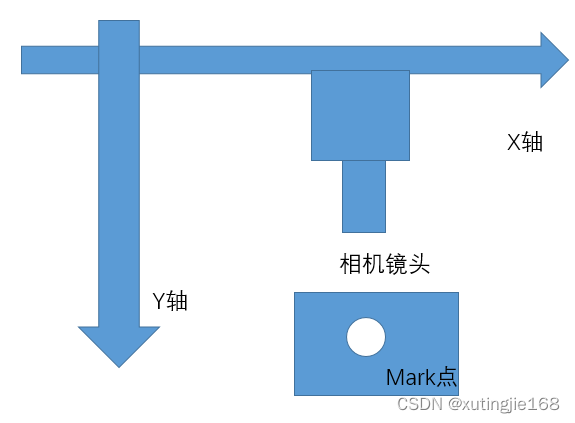
手眼标定眼在手上
1、为什么要用手眼标定 参考手眼标定特别是眼在手上在网上的文章很多,但很多在实际中调试不通。在定位时候,往往希望相机能返回的是机械的世界坐标,而不是相机的的图像坐标。从而间接计算出相机坐标系与机械坐标世界坐标转换矩阵,…...

【数据结构】初始二叉树
满二叉树 每个结点都有左右子树的二叉树。 完全二叉树 从上到下、从左到右排列,不落下一个结点进行排列的二叉树。 二叉树的性质 第i层最多有2(i-1)个结点深度为k的二叉树最多有 2k-1 个结点因为一颗深度为k的满二叉树的结点有2k-1,即nk-1ÿ…...

创建和使用角色(RHCE)
题目: 创建和使用角色 根据下列要求,在 /home/curtis/ansible/roles 中创建名为 apache 的角色: httpd 软件包已安装,设为在系统启动时启用并启动 防火墙已启用并正在运行,并使用允许访问 Web 服务器的规则 模板文件 i…...
)
Leetcode 583 两个字符串的删除操作(经典)
【问题描述】 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 "sea" 变为…...

c#实现工厂模式
可以使用以下代码实现C#中的工厂模式: 首先,定义一个接口作为产品的抽象: public interface IProduct {void Operation(); }然后,创建具体的产品类: public class ConcreteProductA : IProduct {public void Operat…...
c#在设计时调试自定义 Windows 窗体控件
private string demoStringValue null; [Browsable(true)] public string DemoString {get{return this.demoStringValue;}set{demoStringValue value;} } 参考链接 在设计时调试自定义控件 - Windows Forms .NET Framework | Microsoft Learnhttps://learn.microsoft.com/z…...
Ajax 笔记(二)—— Ajax 案例
笔记目录 2. Ajax 综合案例2.1 案例一-图书管理2.1.1 渲染列表2.1.2 新增图书2.1.3 删除图书2.1.4 编辑图书 2.2 案例二-背景图的上传和更换2.2.1 上传2.2.2 更换 2.3 案例三-个人信息设置2.3.1 信息渲染2.3.2 头像修改2.2.3 信息修改2.3.4 提示框 Ajax 笔记: Ajax…...
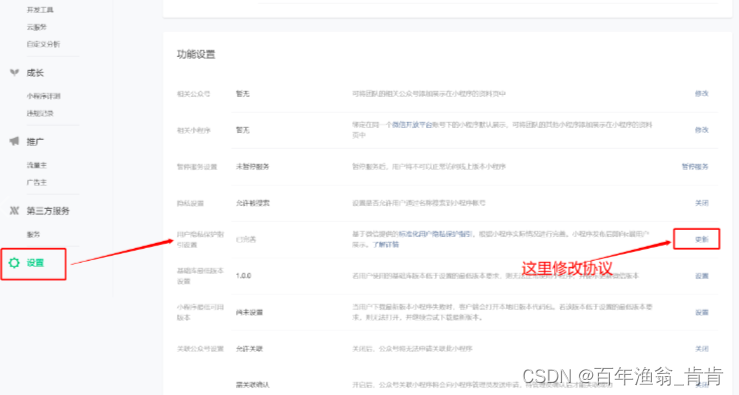
微信小程序隐私协议模板
在 设置 中找到 用户隐私保护 进行更新,如下图: 具体协议补充可参考如下: 为了分辨用户,开发者将在获取你的明示同意后,收集你的微信昵称、头像 为了显示距离,开发者将在获取你的明示同意后,收…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...