数论复习c++
改造序列
题目描述
给定长度为 n n n的序列 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,你可以从中删除一些数,使得删完以后的序列中,所有相邻元素之和均为偶数。请问最少需要删除多少个数?
输入格式
第一行一个整数 T T T,表示测试数据组数 T T T
接下来 T T T组数据,每组数据第一行一个整数 n n n,第二行 n n n个整数,空格分开
输出格式
T T T行,每行一个整数,表示相应数据的答案
样例 #1
样例输入 #1
2
5
2 4 3 6 8
6
3 5 9 7 1 3
样例输出 #1
1
0
提示
记 ∑ n \sum n ∑n为一个数据点中所有 n n n之和
对于 100 % 100\% 100%的数据, 1 ⩽ T ⩽ 100 1\leqslant T\leqslant 100 1⩽T⩽100, 3 ⩽ n ⩽ 1 0 5 3\leqslant n\leqslant 10^5 3⩽n⩽105, 1 ⩽ a i ⩽ 1 0 9 1\leqslant a_i\leqslant 10^9 1⩽ai⩽109, 1 ⩽ ∑ n ⩽ 1 0 5 1\leqslant \sum n\leqslant 10^5 1⩽∑n⩽105
这道题很简单,只需要判断奇数和偶数的的个数,输出最小的那个数就行了,核心代码如下:
while(t--)
{int n,ansa=0,ansb=0; //一定要附初值,不然后面的值不对for(int i=1;i<=n;i++){cin>>a[i];if(a[i]%2==0) //判断奇数偶数的个数{ansa++;}else{ansb++;}/*这里也个可以怎么写:int x;cin>>x;if(x%2==0){ansa++;}else{ansb++;}*/}printf("%d\n",min(ansa,ansb));
}
非倍数求和
题目描述
给定 n , a , b n,a,b n,a,b,求 1 1 1至 n n n之间所有既不是 a a a的倍数也不是 b b b的倍数的数之和。
输入格式
一行,三个整数 n , a , b n,a,b n,a,b
输出格式
一行,一个整数,表示答案
样例 #1
样例输入 #1
10 3 5
样例输出 #1
22
提示
对于 30 % 30\% 30%的数据,$1\leqslant n,a,b\leqslant 10^3 $
对于 60 % 60\% 60%的数据, 1 ⩽ n , a , b ⩽ 1 0 6 1\leqslant n,a,b\leqslant 10^6 1⩽n,a,b⩽106
对于 100 % 100\% 100%的数据, 1 ⩽ n , a , b ⩽ 1 0 9 1\leqslant n,a,b\leqslant 10^9 1⩽n,a,b⩽109
这道题是一道典型的数论题,代码如下:
#include <bits/stdc++.h>
using namespace std;
long long gcd(int a,int b)
{if(b==0){return a;}return gcd(b,a%b);
}
long long lcm(int a,int b)
{return (long long)a*b/gcd(a,b);/*这道题也可以怎么写:return (long long)a*b/__gcd(a,b);这是直接调用库里的gcd手写的gcd表示:那我走*/
}
int main()
{long long n,a,b,ans=0,tota,totb,tott,t;scanf("%lld%lld%lld",&n,&a,&b);ans=(long long)(1+n)*n/2; //高斯求和tota=(long long)(a+n/a*a)*(n/a)/2;totb=(long long)(b+n/b*b)*(n/b)/2;t=lcm(a,b);tott=(t+n/t*t)*(n/t)/2;printf("%lld",ans-tota-totb+tott); //全部-a的倍数-b的倍数+a和b的倍数(这里因为a和b的倍数剪了两遍,所以要把那一遍加回来)return 0;
}
三数不同
题目描述
给定长度为 n n n的序列 a i a_i ai,请计算所有满足以下条件的三元组 ( i , j , k ) (i,j,k) (i,j,k)的个数
- i < j < k i<j<k i<j<k
- a i a_i ai、 a j a_j aj和 a k a_k ak互不相同
输入格式
第一行,一个整数 n n n
第二行 n n n个整数 a i a_i ai
输出格式
一个整数,表示答案
样例 #1
样例输入 #1
4
3 1 4 1
样例输出 #1
2
提示
对于 30 % 30\% 30%的数据, n ⩽ 2 × 100 n\leqslant 2\times 100 n⩽2×100,$a_i\leqslant 2\times 100 $
对于 60 % 60\% 60%的数据, n ⩽ 2 × 1 0 3 n\leqslant 2\times 10^3 n⩽2×103, a i ⩽ 2 × 1 0 3 a_i\leqslant 2\times 10^3 ai⩽2×103
对于 100 % 100\% 100%的数据, 3 ⩽ n ⩽ 2 × 1 0 5 3\leqslant n\leqslant 2\times 10^5 3⩽n⩽2×105, 1 ⩽ a i ⩽ 2 × 1 0 5 1\leqslant a_i\leqslant 2\times 10^5 1⩽ai⩽2×105
这道题是要找出有多少对 三元组 ,这道题的代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N=2e6;
int h[N+10];
long long c(int n,int m) //查找函数
{if(m==2){return (long long)n*(n-1)/2;}else if(m==3){return (long long)n*(n-1)*(n-2)/6;}
}
int main()
{int n,ans=0;scanf("%d",&n);for(int i=1;i<=n;i++){int x;scanf("%d",&x);h[x]++;}long long tot=c(n,3); //找zzz的情况for(int i=1;i<=N;i++){if(h[i]>=2){tot-=c(h[i],2)*(n-h[i]); //找zzy的情况,前两个找到了,最后一个随便找一个就行了}if(h[i]>=3){tot-=c(h[i],3); //找zzz的情况}}printf("%lld",tot);return 0;
}
相关文章:

数论复习c++
改造序列 题目描述 给定长度为 n n n的序列 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,你可以从中删除一些数,使得删完以后的序列中,所有相邻元素之和均为偶数。请问最少需要删除多少个数? 输入格式 第一行…...

Java try-with-resources 显性 与 隐性 关闭 资源
try-with-resources 是 Java 7 引入的一个语言特性,用于简化资源管理的代码,特别是在处理需要关闭的资源(如文件、网络连接、数据库连接等)时。try-with-resources 允许您在 try 语句中声明需要关闭的资源,这些资源会在…...
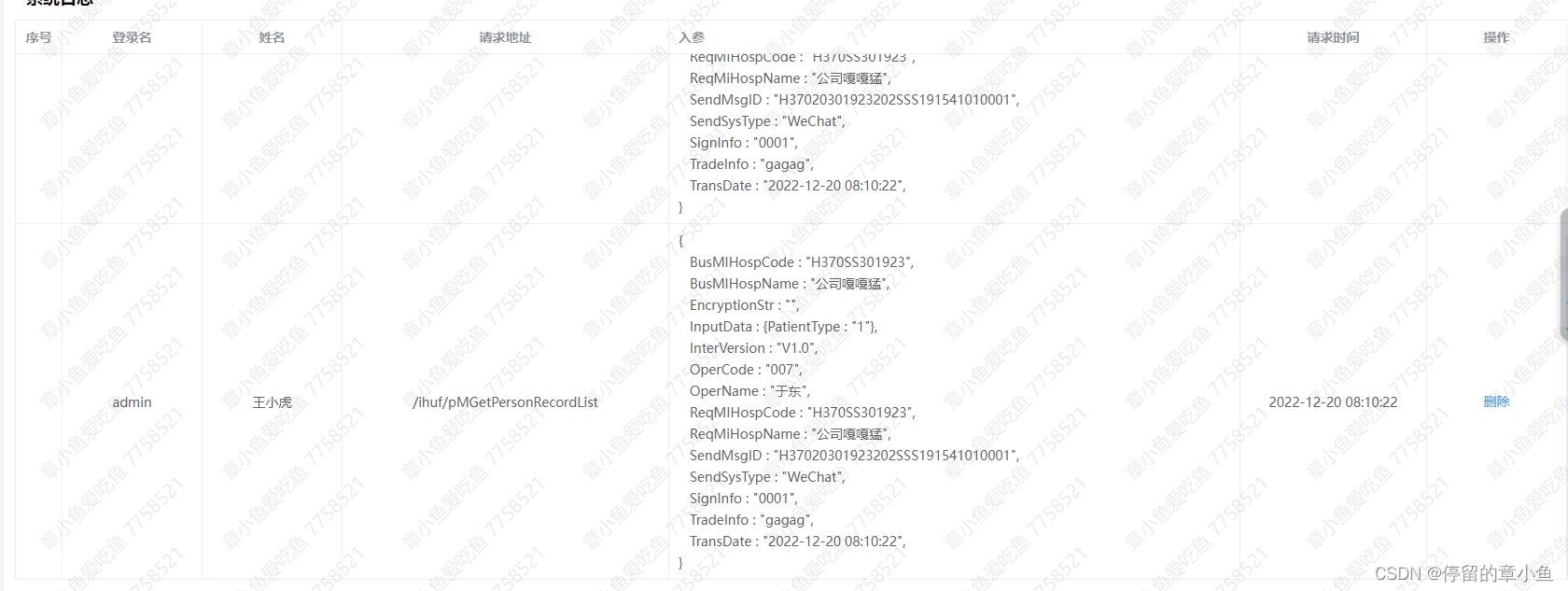
Vue在页面输出JSON对象,测试接口可复制使用
效果图: 数据处理前: 数据处理后: 代码实现: HTML: <el-table height"600" :data"tableData" border style"width: 100%" tooltip-effect"dark" size"mini"><el-…...
)
【STM32】FreeRTOS开启后,不再进入主函数的while(1)
开启freertos后,想在主函数的while(1)中实现led的翻转,发现无法实现。 int main(void) {/* USER CODE BEGIN 1 *//* USER CODE END 1 *//* MCU Configuration--------------------------------------------------------*//* Reset of all peripherals, …...

Python+Selenium+Unittest 之selenium11--WebDriver操作方法1-常用操作
目录 1、send_keys("输入的内容") (输入文字) 2、clear() (清除元素内的内容) 3、click()(点击元素) 4、quit()关闭浏览器 5、refresh()(刷新浏览器页面) 6、set_window_size()和用 maxim…...

气液固三相线识别—Langmuir部分复现
关注 M r . m a t e r i a l , \color{Violet} \rm Mr.material\ , Mr.material...
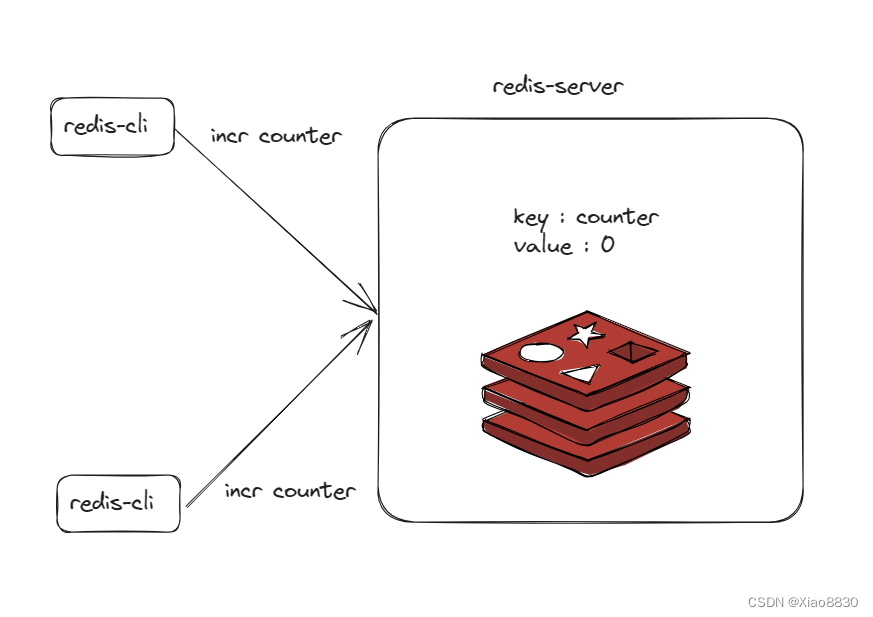
Redis——常见数据结构与单线程模型
Redis中的数据结构 Redis中所有的数据都是基于key,value实现的,这里的数据结构指的是value有不同的类型。 当前版本Redis支持10种数据类型,下面介绍常用的五种数据类型 底层编码 Redis在实现上述数据结构时,会在源码有特定的…...
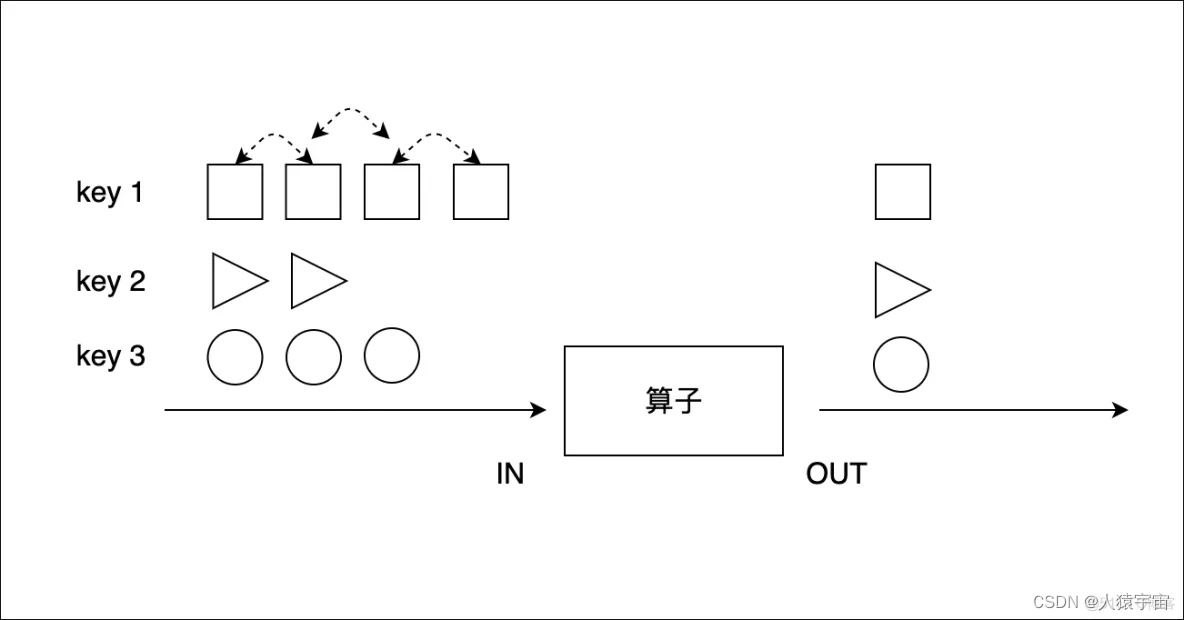
大数据-玩转数据-Flink-Transform
一、Transform 转换算子可以把一个或多个DataStream转成一个新的DataStream.程序可以把多个复杂的转换组合成复杂的数据流拓扑. 二、基本转换算子 2.1、map(映射) 将数据流中的数据进行转换, 形成新的数据流,消费一个元素并产出一个元素…...

Java泛型集合简明教程
前言 我们编写一个数组并对数组进行排序,不管是对浮点型数组、整型数组、字符串数组或者是其他任何类型的数组进行排序,我们可以利用方法重载的方式,针对每种类型的数组分别编写一个排序方法,需要为几种类型的数组排序࿰…...

Prometheus-RabbitMQ Exporter
文章目录 一、介绍监控插件两个插件的区别一、 官方插件 rabbitmq_prometheus1 配置 RabbitMQ 集群名称2 授权使用插件2.1 配置文件方式2.2 命令行方式3 监听地址和端口4 RabbitMQ 插件获取指标的频率5 配置到 Prometheus6 关于聚合指标和每个对象指标6.1 获取聚合指标 `/metri…...

flink读取kafka数据存储iceberg
1、说明 使用flink实时的读取kafka的数据,并且实时的存储到iceberg中。好处是可以一边存数据,一边查询数据。当然使用clickhouse也可以实现数据的既存既取。而hive数据既存既读则会有问题。iceberg中数据读写数据都是从快照中开始的,读和写对…...

文章二:分支管理策略 - 分支玩转:Git分支管理实战
开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun 概述 在软件开发中,版本控制是一项至关重要的工作。Git作为目前最受欢迎的分布式版本控制系统&…...

JS dom元素和鼠标位置之间的一系列属性快速参考
clientHeight 获取对象的高度,不计算任何边距、边框、滚动条,但包括该对象的补白。 clientLeft 获取 offsetLeft 属性和客户区域的实际左边之间的距离。 clientTop 获取 offsetTop 属性和客户区域的实际顶端之间的距离。 clie…...

【剑指 Offer 39】数组中超过一半的数字
题目: 数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例: 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2 思考: 方法一:投…...

list.stream.filter,List<List>转换为List
1.filter过滤 返回符合查询条件的集合//过滤所有deviceType为1的List<DeviceWorkTimeEntity> list entities.stream().filter(a -> "1".equals(a.getDeviceType())).toList(); 2.List<List>转换为List 可以使用流(Stream)的flatMap操作 public cl…...

手机里视频太大怎么压缩?压缩教程分享
现在视频文件的体积越来越大了,动不动就是几个GB起步,如果后期再剪辑处理一下,更是会占据更多的设备空间了,还会导致我们传输受到限制,这时候就需要我们对视频进行压缩处理,下面给大家分享几个简单的方法&a…...

Spring-Cloud-Loadblancer详细分析_3
前两篇文章介绍了加载过程,本文从Feign的入口开始分析执行过程,还是从FeignBlockingLoadBalancerClient.execute来入手 public class FeignBlockingLoadBalancerClient implements Client {private static final Log LOG LogFactory.getLog(FeignBlock…...
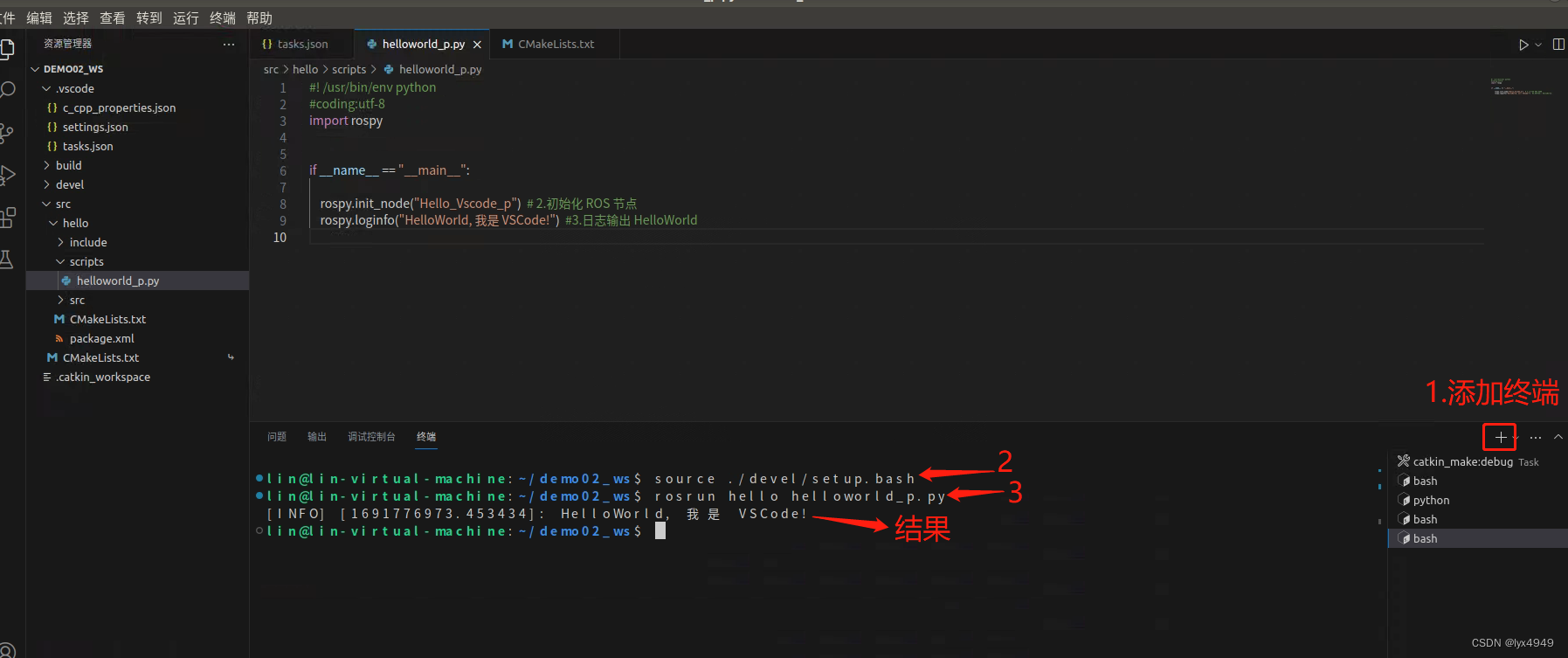
使用 VScode 开发 ROS 的Python程序(简例)
一、任务介绍 本篇作为ROS学习的第二篇,是关于如何在Ubuntu18.04中使用VSCode编写一个Python程序,输出“Hello!”的内容介绍。 首先我们来了解下ROS的文件系统,ROS文件系统级指的是在硬盘上ROS源代码的组织形式,其结构…...

2022年03月 C/C++(一级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:双精度浮点数的输入输出 输入一个双精度浮点数,保留8位小数,输出这个浮点数。 时间限制:1000 内存限制:65536 输入 只有一行,一个双精度浮点数。 输出 一行,保留8位小数的浮点数。 样例输…...

HarmonyOS/OpenHarmony应用开发-ArkTSAPI系统能力SystemCapability列表
SysCap,全称SystemCapability,即系统能力,指操作系统中每一个相对独立的特性。 开发者使用某个接口进行开发前,建议先阅读系统能力使用说明,了解Syscap的定义和使用指导。 说明 当前列表枚举出3.1 Beta版本中支持的…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
