组合求和-矩阵连乘所有加括号方式_2023_08_12
矩阵链加括号方式总数
- 前言
矩阵链乘积的瓶颈在于其标量运算的次数,不同的结合次序对其时间性能影响远大于矩阵乘积运算本身,可以看到许多教材上把求解矩阵标量运算的最优解作为动态规划的示例,问题隐含动态规划两大特征: 最优子结构及重叠子问题。诸多教材上对此作了详细的描述和解释,此问题本文不再做过多讨论。
本文旨在讨论给定某个矩阵,讨论其不同加括号的方式,要求求出所有可能加括号的数量,并就此问题引出Catalan Number的一般概念。
- 问题描述
给定矩阵<M1,M2,…Mn>,探索其可能加括号的方式。为了解决此问题,从最简单形式开始逐步进行研究其解的形式,假定只有一个矩阵M1, 那么其加括号的方式为1。同理,给定两个矩阵,显而易见,其加括号方式总数也为1。那么对于n个矩阵,那么其加括号的总数为几多呢?
为了探讨此一般解问题,假定第 k个矩阵把n个矩阵分两部分,表示第一部分矩阵为<M1,M2,…Mk>,表示第二部分矩阵为<Mk+1,M2,…Mn>。规定P(n)代表n个矩阵所有可能加括号方式的综合,可采用下列递归方程式表示其值,
P ( n ) = ∑ k = 1 n − 1 P ( k ) ∗ P ( n − k ) ; ( n ≥ 2 ) P(n)=\sum_{k=1}^{n-1}{P(k)*P(n-k)} ;\ (n\geq2) P(n)=k=1∑n−1P(k)∗P(n−k); (n≥2)
很明显,问题纳入分治的范畴,它之和子问题的长度相关的乘积相关,矩阵本身对其没有影响,P(k)代表k个矩阵可能的加括号方式,P(n-k)代表n-k个矩阵加括号方式,P(k)*P(n-k)代表以k为分界的所有加括号的方式,而P(k)*P(n-k)对于所有的k的方式求和,便是P(n)的值。
- 暴力递归方案(无记忆递归)
上述表达式为经典的递归求和方式,可以利用暴力求解途径,对每个n和k分割进行求解,最后求和即可得到最终的结果,它的时间复杂度与求解Catalan number相同(Program for nth Catalan Number - GeeksforGeeks),采用暴力方法求解的时间复杂度为Ω(4n/n3/2),暴力解决方法不是理想求解问题的方式,下一篇幅中将引入动态规划的途径求解。
通过观察发现,n==1的情况下构成递归的基础解,函数直接返回1作为递归结束点。定义 sum为不同加括号的方式,它可以与上级栈的乘积和进行累加。
深入探索就会发现f(n-i)和f(i)递归函数存在可能的重合部分,这将导致每次递归都到出口点,对函数计算构成严重浪费的行为。
int find_matrix_complete_parenthesis_recursion(int n)
{int i;int sum;if(n==1){return 1;}sum=0;for(i=1;i<n;i++){sum += find_matrix_complete_parenthesis_recursion(n - i) * \find_matrix_complete_parenthesis_recursion(i);}return sum;}
- 动态规划方案
上节讨论展开过程中,发现求解过程存在诸多重复子问题,虽然求和过程未呈现显著的最优子问题特征,原因在于其行为是对不同问题进行求和,求和过程本来就无所谓的最优/最劣的过程,它关注的是加括号方式的不同类型的求和。
int find_matrix_complete_parenthesis_dp(int n)
{int i;int j;int dp[n+1];memset(dp,0,sizeof(dp));dp[1]=1;for(i=2;i<=n;i++){for(j=1;j<i;j++){dp[i]+=dp[j]*dp[i-j];}}return dp[n];
}
- 总结
求解组合总和,一般不涉及到求解最大或最小值的操作,其过程汇总也不涉及到选择的代价,因为需要对所有的可能性选择进行求和汇总。
参考资料
- Program for nth Catalan Number - GeeksforGeeks
相关文章:

组合求和-矩阵连乘所有加括号方式_2023_08_12
矩阵链加括号方式总数 前言 矩阵链乘积的瓶颈在于其标量运算的次数,不同的结合次序对其时间性能影响远大于矩阵乘积运算本身,可以看到许多教材上把求解矩阵标量运算的最优解作为动态规划的示例,问题隐含动态规划两大特征: 最优子…...
《3D 数学基础》12 几何图元
目录 1 表达图元的方法 1.1 隐式表示法 1.2 参数表示 1.3 直接表示 2. 直线和射线 2.1 射线的不同表示法 2.1.1 两点表示 2.1.2 参数表示 2.1.3 相互转换 2.2 直线的不同表示法 2.2.1 隐式表示法 2.2.2 斜截式 2.2.3 相互转换 3. 球 3.1 隐式表示 1 表达图元的方…...
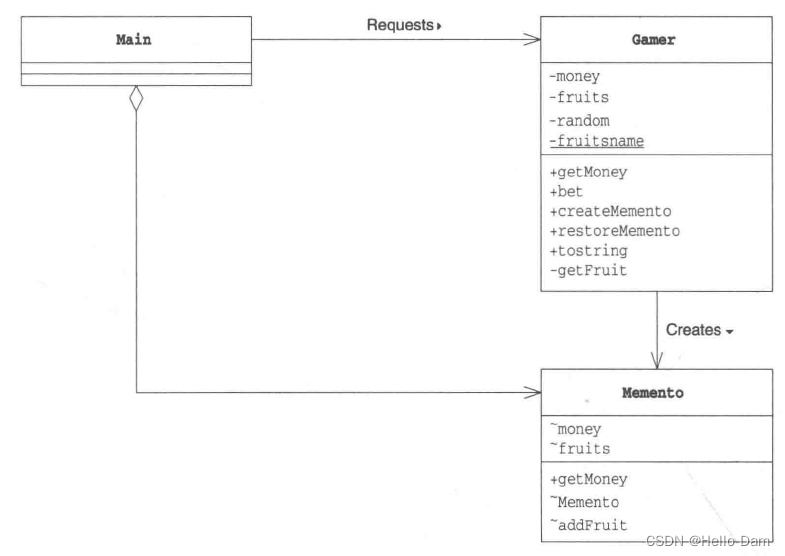
【设计模式——学习笔记】23种设计模式——备忘录模式Memento(原理讲解+应用场景介绍+案例介绍+Java代码实现)
案例引入 游戏角色有攻击力和防御力,在大战Boss前保存自身的状态(攻击力和防御力),当大战Boss后攻击力和防御力下降,可以从备忘录对象恢复到大战前的状态 传统设计方案 针对每一种角色,设计一个类来存储该角色的状态 【分析】…...
致谢丨感谢有你,JumpServer开源项目九周年致谢名单
2014年到2023年,JumpServer开源项目已经走过了九年的时间。感谢以下社区贡献者对JumpServer项目的帮助和支持。 因为有你,一切才能成真。 JumpServer开源项目贡献者奖杯将于近日邮寄到以上贡献者手中,同时JumpServer开源项目组还准备了一份小…...
使用 Python 和 Flask 构建简单的 Restful API 第 1 部分
一、说明 我将把这个系列分成 3 或 4 篇文章。在本系列的最后,您将了解使用flask构建 restful API 是多么容易。在本文中,我们将设置环境并创建将显示“Hello World”的终结点。 我假设你的电脑上安装了python 2.7和pip。我已经在python 2.7上测试了本文…...
)
【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(2/2)
一、说明 在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。 (二-五)见 六、稀疏分类交叉熵损失 稀疏分类交叉熵损失类似于分类交叉熵损失,但在真实标签作为整数而不是独热编码提…...

Hazel 引擎学习笔记
目录 Hazel 引擎学习笔记学习方法思考引擎结构创建工程程序入口点日志系统Premake\MD没有 cpp 文件的项目会出错include 到某个库就要包含这个库的路径,注意头文件展开 事件系统 获取和利用派生类信息预编译头文件抽象窗口类和 GLFWgit submodule addpremake 脚本禁…...
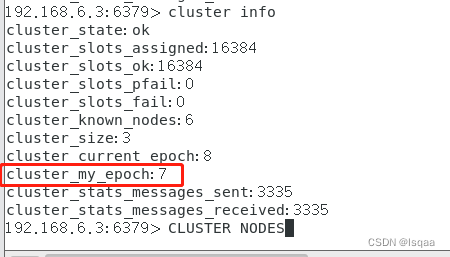
Linux系统下Redis3.2集群
本节主要学习reids主从复制的概念,作用,缺点,流程,搭建,验证,reids哨兵模式的概念,作用,缺点,结构,搭建,验证等。 文章目录 一、redis主从复制 …...
Android图形-合成与显示-SurfaceTestDemo
目录 引言: 主程序代码: 结果呈现: 小结: 引言: 通过一个最简单的测试程序直观Android系统的native层Surface的渲染显示过程。 主程序代码: #include <cutils/memory.h> #include <utils/L…...

高压放大器怎么设计(高压放大器设计方案)
高压放大器是一种用于将低电压信号转换成高电压信号的电子设备,广泛应用于通信、雷达、医疗设备等领域。在设计高压放大器时,需要考虑多种因素,如输入输出信号的特性、电路结构的选择、电源和负载匹配等。本文将介绍高压放大器的设计方法和注…...

SpringBoot yml配置注入
yaml语法学习 1、配置文件 SpringBoot使用一个全局的配置文件 , 配置文件名称是固定的 application.properties 语法结构 :keyvalue application.yml 语法结构 :key:空格 value 配置文件的作用:修改SpringBoot自动…...

中科亿海微乘法器(LPMMULT)
引言 FPGA(可编程逻辑门阵列)是一种可在硬件级别上重新配置的集成电路。它具有灵活性和可重构性,使其成为处理各种应用的理想选择,包括数字信号处理、图像处理、通信、嵌入式系统等。在FPGA中,乘法器是一种重要的硬件资…...
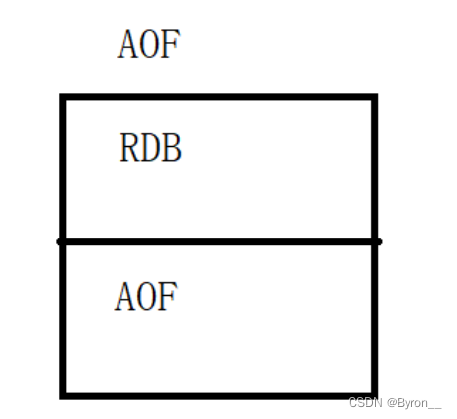
Redis_持久化(AOF、RDB)
6. Redis AOF 6.1 简介 目前,redis的持久化主要应用AOF(Append Only File)和RDF两大机制,AOF以日志的形式来记录每个写操作(增量保存),将redis执行过的所有指令全部安全记录下来(读…...
开源数据库Mysql_DBA运维实战 (部署服务篇)
前言❀ 1.数据库能做什么 2.数据库的由来 数据库的系统结构❀ 1.数据库系统DBS 2.SQL语言(结构化查询语言) 3.数据访问技术 部署Mysql❀ 1.通过rpm安装部署Mysql 2.通过源码包安装部署Mysql 前言❀ 1.数据库能做什么 a.不论是淘宝,吃鸡,爱奇艺…...
【Java学习】System.Console使用
背景 在自学《Java核心技术卷1》的过程中看到了对System.Console的介绍,编写下列测试代码, public class ConsoleTest {public static void main(String[] args) {Console cs System.console();String name cs.readLine("AccountInfo: ");…...

从零学算法154
154.已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4] 若旋转 7 次&#…...

95 | Python 设计模式 —— 策略模式
策略模式(Strategy Pattern) 引言 策略模式是一种行为型设计模式,它定义了一系列的算法,并将每个算法封装在独立的策略类中,使得这些算法可以相互替换,而不影响客户端的使用。策略模式可以让客户端根据不同的需求选择不同的算法,从而使得系统更加灵活和可扩展。 在本…...
)
【BASH】回顾与知识点梳理(十九)
【BASH】回顾与知识点梳理 十九 十九. 循环 (loop)19.1 while do done, until do done (不定循环)19.2 for...do...done (固定循环)19.3 for...do...done 的数值处理(C写法)19.4 搭配随机数与数组的实验19.5 shell script 的追踪与 debug19.6 what_to_eat-2.sh debug结果解析 该…...
Selenium之css怎么实现元素定位?
世界上最远的距离大概就是明明看到一个页面元素站在那里,但是我却定位不到!! Selenium定位元素的方法有很多种,像是通过id、name、class_name、tag_name、link_text等等,但是这些方法局限性太大, 随着自动…...
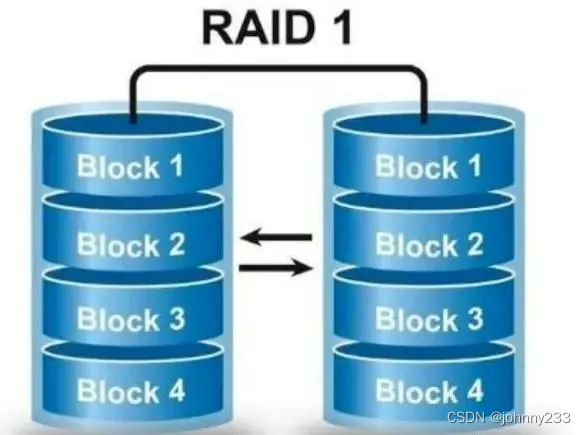
计算机基础之RAID技术
概述 RAID,Redundant Array of Independent Disks,独立磁盘冗余阵列,一种把多块独立的硬盘(物理硬盘)按不同的方式组合起来形成一个硬盘组(逻辑硬盘),从而提供比单个硬盘更高的存储…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
