数据结构:交换排序
冒泡排序
起泡排序,别名“冒泡排序”,该算法的核心思想是将无序表中的所有记录,通过两两比较关键字,得出升序序列或者降序序列。
算法步骤
- 比较相邻的元素。如果第一个元素大于第二个元素,就交换它们。
- 对每一对相邻的元素作相同的操作,从开始第一对到末尾的最后一对。
- 针对所有的元素重复以上操作,每次出来最后一个
算法理解
例如,对无序表{49,38,65,97,76,13,27,49}进行升序排序的具体实现过程如图 1 所示:

图 1 第一次起泡
如图 1 所示是对无序表的第一次起泡排序,最终将无序表中的最大值 97 找到并存储在表的最后一个位置。具体实现过程为:
- 首先 49 和 38 比较,由于 38<49,所以两者交换位置,即从(1)到(2)的转变;
- 然后继续下标为 1 的同下标为 2 的进行比较,由于 49<65,所以不移动位置,(3)中 65 同 97 比较得知,两者也不需要移动位置;
- 直至(4),97 同 76 进行比较,76<97,两者交换位置,如(5)所示;
- 同样 97>13(5)、97>27(6)、97>49(7),所以经过一次冒泡排序,最终在无序表中找到一个最大值 97,第一次冒泡结束;
由于 97 已经判断为最大值,所以第二次冒泡排序时就需要找出除 97 之外的无序表中的最大值,比较过程和第一次完全相同。

经过第二次冒泡,最终找到了除 97 之外的又一个最大值 76,比较过程完全一样,这里不再描述。
通过一趟趟的比较,一个个的“最大值”被找到并移动到相应位置,直到检测到表中数据已经有序,或者比较次数等同于表中含有记录的个数,排序结束,这就是起泡排序。
代码实现
#include "iostream"
using namespace std;void swap(int *a, int *b){//交换a和b的位置int temp;temp = *a;*a = *b;*b = temp;
}
int main()
{int array[8] = {49,38,65,97,76,13,27,49};//有多少记录,就需要多少次冒泡,当比较过程,所有记录都按照升序排列时,排序结束for (int i = 0; i < 8; i++){int key=0;//每次开始冒泡前,初始化 key 值为 0//每次起泡从下标为 0 开始,到 8-i 结束for (int j = 0; j+1<8-i; j++){if (array[j] > array[j+1]){key=1;swap(&array[j], &array[j+1]);}}//如果 key 值为 0,表明表中记录排序完成if (key==0) {break;}}for (i = 0; i < 8; i++){cout << array[i] << " ";}return 0;
}
运行结果:
13 27 38 49 49 65 76 97
总结
使用起泡排序算法,其时间复杂度同实际表中数据的无序程度有关。若表中记录本身为正序存放,则整个排序过程只需进行 n-1(n 为表中记录的个数)次比较,且不需要移动记录;若表中记录为逆序存放(最坏的情况),则需要 n-1趟排序,进行 n(n-1)/2 次比较和数据的移动。所以该算法的时间复杂度为O(n2)。
快速排序
快速排序本质上是可以说是冒泡排序基础上的递归分治法,它也是分治算法在排序算法上的一种经典应用。
算法思想
快速排序是通过多次比较和交换来实现有序的。在一次排序中把将要排序的元素分成两个独立的子数组,其中一个子数组的所有元素全大于另一个组数组的所有元素,然后继续递归排序这两部分。
算法思想步骤:
- 从序列中挑出一个元素,称之为边界或者基准
- 重新排序数列,所有元素比基准值小的放在基准前面,所有元素比基准值大的放在基准后面(相同的数可以放在任意一边)。这个操作结束后,该基准就处于序列的中间位置,这个操作称之为分区操作
- 递归吧小于基准元素的组数组和大于基准元素的子数组排序
算法理解

代码实现
#include "iostream"
using namespace std;#define MAX 9
//单个记录的结构体
typedef struct {int key;
}SqNote;
//记录表的结构体
typedef struct {SqNote r[MAX];int length;
}SqList;
//此方法中,存储记录的数组中,下标为 0 的位置时空着的,不放任何记录,记录从下标为 1 处开始依次存放
int Partition(SqList *L,int low,int high){L->r[0]=L->r[low];int pivotkey=L->r[low].key;//直到两指针相遇,程序结束while (low<high) {//high指针左移,直至遇到比pivotkey值小的记录,指针停止移动while (low<high && L->r[high].key>=pivotkey) {high--;}//直接将high指向的小于支点的记录移动到low指针的位置。L->r[low]=L->r[high];//low 指针右移,直至遇到比pivotkey值大的记录,指针停止移动while (low<high && L->r[low].key<=pivotkey) {low++;}//直接将low指向的大于支点的记录移动到high指针的位置L->r[high]=L->r[low];}//将支点添加到准确的位置L->r[low]=L->r[0];return low;
}
void QSort(SqList *L,int low,int high){if (low<high) {//找到支点的位置int pivotloc=Partition(L, low, high);//对支点左侧的子表进行排序QSort(L, low, pivotloc-1);//对支点右侧的子表进行排序QSort(L, pivotloc+1, high);}
}
void QuickSort(SqList *L){QSort(L, 1,L->length);
}
int main() {SqList *L = new SqList;L->length=8;L->r[1].key=49;L->r[2].key=38;L->r[3].key=65;L->r[4].key=97;L->r[5].key=76;L->r[6].key=13;L->r[7].key=27;L->r[8].key=49;QuickSort(L);for (int i=1; i<=L->length; i++) {cout << L->r[i].key << " ";}return 0;
}
运行结果:
13 27 38 49 49 65 76 97
总结
快速排序算法的时间复杂度为O(nlogn),是所有时间复杂度相同的排序方法中性能最好的排序算法。
相关文章:

数据结构:交换排序
冒泡排序 起泡排序,别名“冒泡排序”,该算法的核心思想是将无序表中的所有记录,通过两两比较关键字,得出升序序列或者降序序列。 算法步骤 比较相邻的元素。如果第一个元素大于第二个元素,就交换它们。对每一对相邻…...
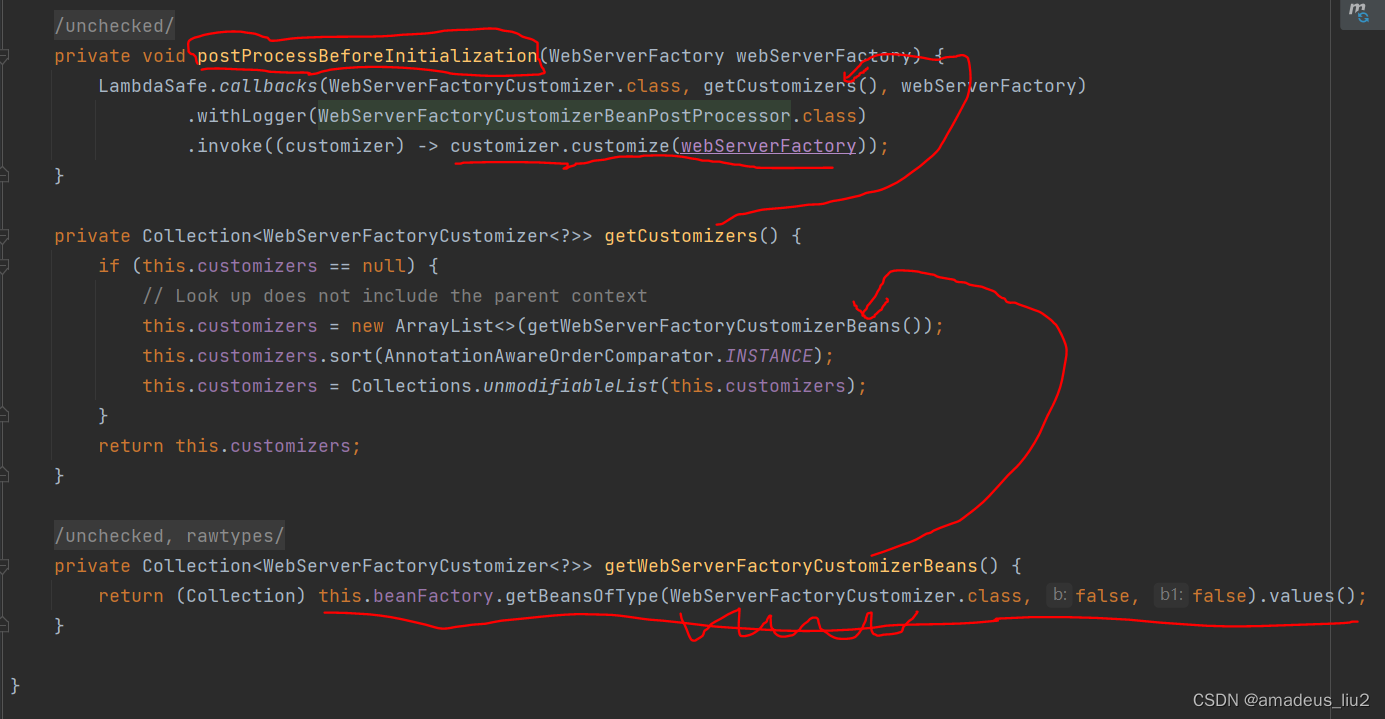
SpringBoot复习:(42)WebServerCustomizer的customize方法是在哪里被调用的?
ServletWebServletAutoConfiguration类定义如下: 可以看到其中通过Import注解导入了其内部类BeanPostProcessorRegister。 BeanPostProcessor中定义的registerBeanDefinition方法会被Spring容器调用。 registerBeanDefinitions方法调用了RegistrySyntheticBeanIf…...

年至年的选择仿elementui的样式
组件:<!--* Author: liuyu liuyuxizhengtech.com* Date: 2023-02-01 16:57:27* LastEditors: wangping wangpingxizhengtech.com* LastEditTime: 2023-06-30 17:25:14* Description: 时间选择年 - 年 --> <template><div class"yearPicker"…...
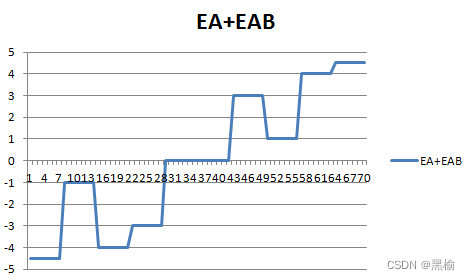
分类过程中的一种遮挡现象
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点,AB训练集各由6张二值化的图片组成,让A,B中各有3个点,且不重合,统计迭代次数并排序。 其中有10组数据 差值结构 迭代次数 构造平均列A 构造平均列AB…...

下一代服务架构:单体架构-->分布式架构-->微服务(DDD)-->软件定义架构(SDF with GraphEngine)
参考:自己实现一个SQL解析引擎_曾经的学渣的博客-CSDN博客...
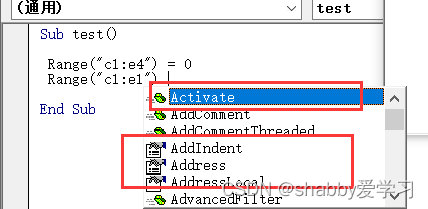
excel 之 VBA
1、excel和VBA 高效办公,把重复性的工作写成VBA代码(VB代码的衍生物,语法和VBA相同)。 首先打开开发工具模式,如果没有选显卡,需要手动打开 打开程序编辑界面 快捷键 altF11一般操作 程序调试…...
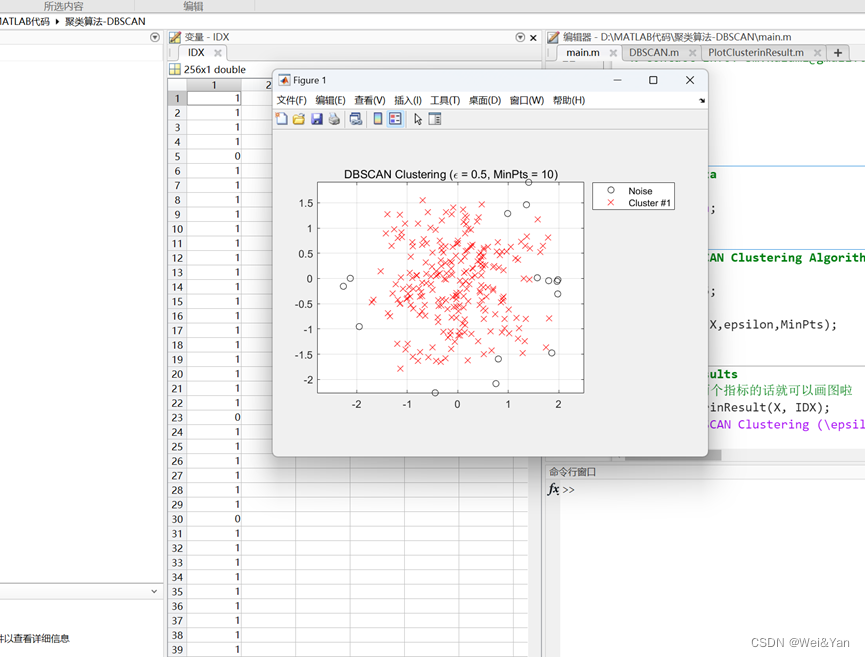
【数学建模】--聚类模型
聚类模型的定义: “物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计,分析或预测;也可以探究不…...

css3新增选择器总结
目录 一、属性选择器 二、结构伪类选择器 三、伪元素选择器 四、UI状态伪类选择器 五、反选伪类选择器 六、target选择器 七、父亲选择器、后代选择器 八、相邻兄弟选择器、兄弟们选择器 一、属性选择器 (除IE6外的大部分浏览器支持) E&#…...

0基础学C#笔记10:归并排序法
文章目录 前言一、递归的方式二、代码总结 前言 将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很…...

nlohmann json:通过for遍历object和array
object和array可以使用数for进行遍历: #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;auto checkJsonType(json& x) {if(x.type() == json::value_t::null){cout<<x<<" is null&quo…...

适配器模式:将不兼容的接口转换为可兼容的接口
适配器模式:将不兼容的接口转换为可兼容的接口 什么是适配器模式? 适配器模式是一种结构型设计模式,用于将一个类的接口转换为客户端所期望的另一个接口。它允许不兼容的类能够合作,使得原本由于接口不匹配而无法工作的类能够一…...
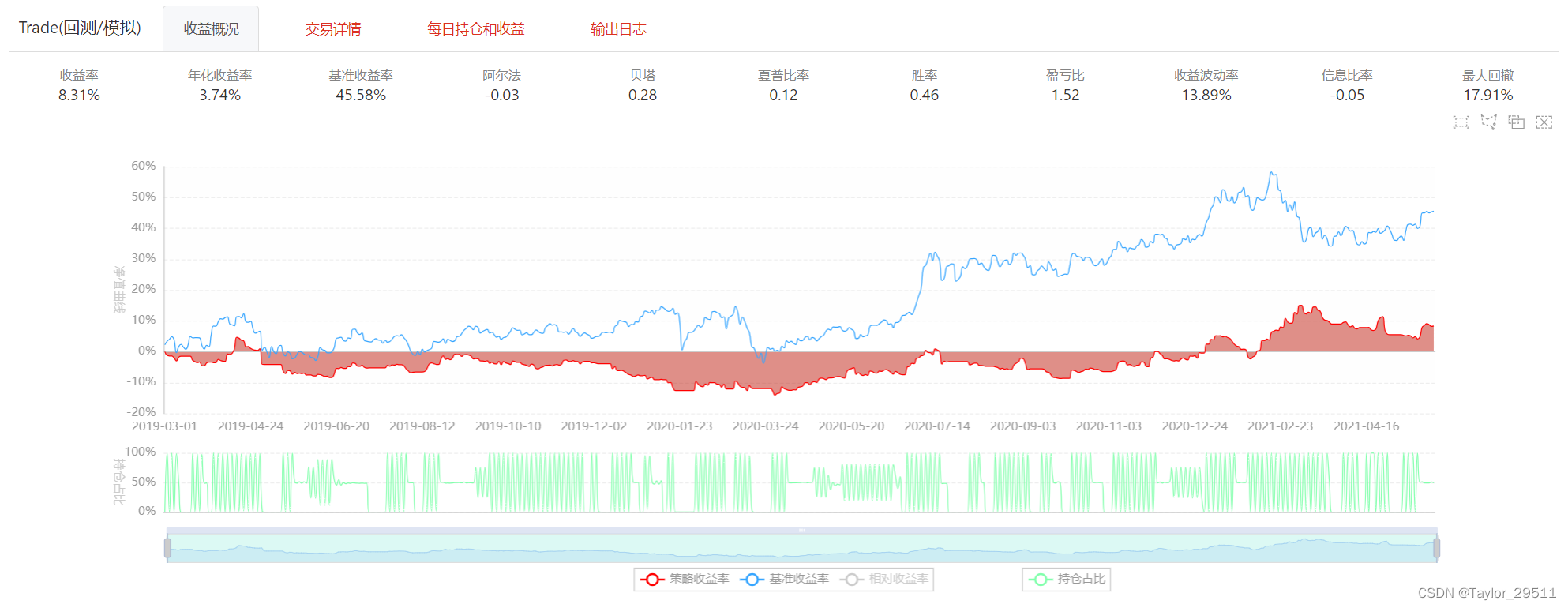
【量化课程】07_量化回测
文章目录 7.1 pandas计算策略评估指标数据准备净值曲线年化收益率波动率最大回撤Alpha系数和Beta系数夏普比率信息比率 7.2 聚宽平台量化回测实践平台介绍策略实现 7.3 Backtrader平台量化回测实践Backtrader简介Backtrader量化回测框架实践 7.4 BigQuant量化框架实战BigQuant简…...
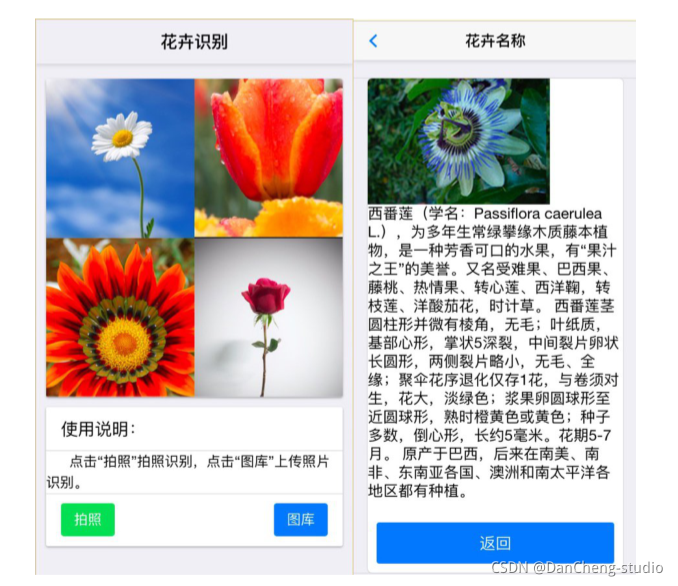
竞赛项目 深度学习花卉识别 - python 机器视觉 opencv
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &a…...
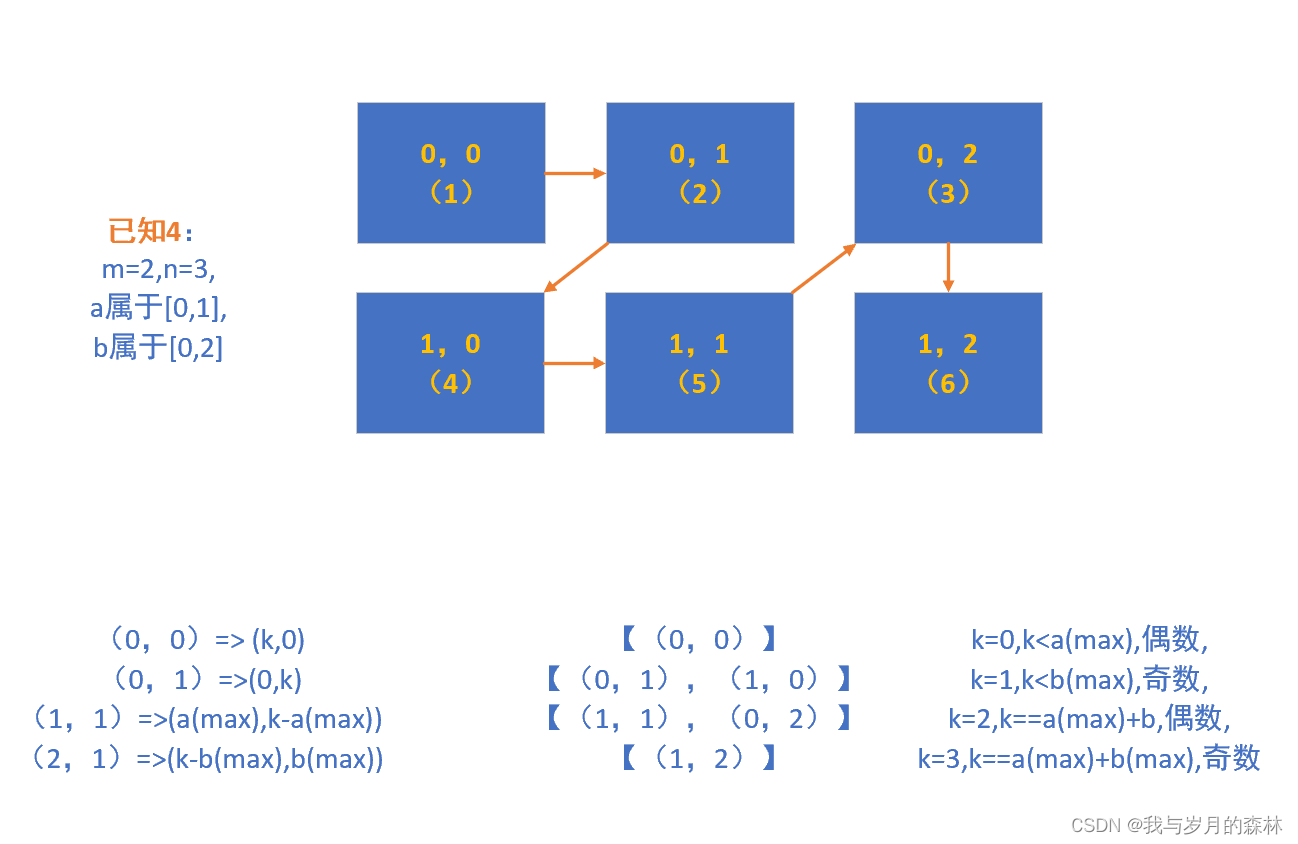
用对角线去遍历矩阵
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 用对角线遍历矩阵https://leetcode.c…...
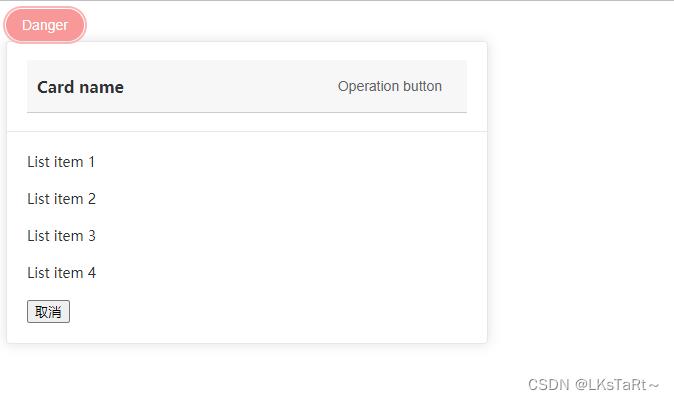
【vue】点击按钮弹出卡片,点击卡片中的取消按钮取消弹出的卡片(附代码)
实现思路: 在按钮上绑定一个点击事件,默认是true;在export default { }中注册变量给卡片标签用v-if判断是否要显示卡片,ture则显示;在卡片里面写好你想要展示的数据;给卡片添加一个取消按钮,绑…...

【K8S】pod 基础概念讲解
目录 Pod基础概念:在Kubrenetes集群中Pod有如下两种使用方式:pause容器使得Pod中的所有容器可以共享两种资源:网络和存储。总结:kubernetes中的pause容器主要为每个容器提供以下功能:Kubernetes设计这样的Pod概念和特殊…...
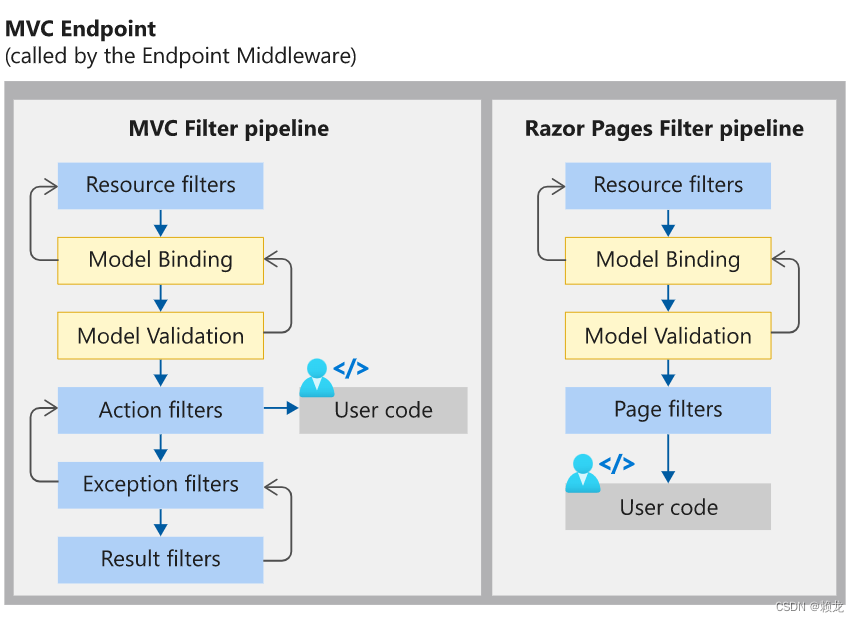
ASP.NET Core中间件记录管道图和内置中间件
管道记录 下图显示了 ASP.NET Core MVC 和 Razor Pages 应用程序的完整请求处理管道 中间件组件在文件中添加的顺序Program.cs定义了请求时调用中间件组件的顺序以及响应的相反顺序。该顺序对于安全性、性能和功能至关重要。 内置中间件记录 内置中间件原文翻译MiddlewareDe…...

[系统安全] 五十二.DataCon竞赛 (1)2020年Coremail钓鱼邮件识别及分类详解
您可能之前看到过我写的类似文章,为什么还要重复撰写呢?只是想更好地帮助初学者了解病毒逆向分析和系统安全,更加成体系且不破坏之前的系列。因此,我重新开设了这个专栏,准备系统整理和深入学习系统安全、逆向分析和恶意代码检测,“系统安全”系列文章会更加聚焦,更加系…...

Android学习之路(3) 布局
线性布局LinearLayout 前几个小节的例程中,XML文件用到了LinearLayout布局,它的学名为线性布局。顾名思义,线性布局 像是用一根线把它的内部视图串起来,故而内部视图之间的排列顺序是固定的,要么从左到右排列…...
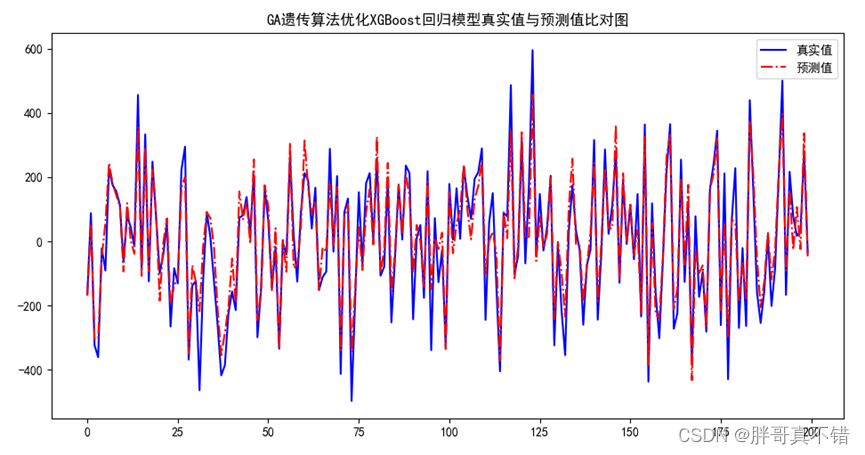
Python实现GA遗传算法优化XGBoost回归模型(XGBRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
