day9 | 28. 实现 strStr()、459.重复的子字符串
目录:
解题及思路学习
28. 实现 strStr()
https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 ****。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
思考:字符串匹配,可以直接暴力方法。但是这题肯定是kmp算法。
前缀表:前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
**前缀表是如何记录的呢?**什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
前缀表要求的就是相同前后缀的长度。
所以字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2。 等等…。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pXWB2jJR-1691982232460)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/0577fe82-fba0-498e-8995-e7eca0fbc040/Untitled.png)]
前缀表可以告诉我们匹配失败之后跳到哪里重新开始匹配。
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。
如何计算前缀表
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mC760OQe-1691982232464)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/87bd2181-9cb1-4836-ad3f-6a2dd4a50f59/Untitled.png)]
可以看出模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
KMP算法的时间复杂度是O(n+m)的。暴力的解法显而易见是O(n × m),所以KMP在字符串匹配中极大地提高了搜索的效率。
构造next数组
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
前缀表统一减一的操作
class Solution {
public:void getNext(int* next, const string& s) {int j = -1;next[0] = j;for(int i = 1; i < s.size(); i++) { // 注意i从1开始while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退}if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;}next[i] = j; // 将j(前缀的长度)赋给next[i]}}int strStr(string haystack, string needle) {if (needle.size() == 0) {return 0;}int next[needle.size()];getNext(next, needle);int j = -1; // // 因为next数组里记录的起始位置为-1for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配j = next[j]; // j 寻找之前匹配的位置}if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动j++; // i的增加在for循环里}if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串treturn (i - needle.size() + 1);}}return -1;}
};
- 时间复杂度: O(n + m)
- 空间复杂度: O(m), 只需要保存字符串needle的前缀表
前缀表(不减一)C++实现
i表示后缀末尾,ji傲视前缀末尾。
class Solution {
public:void getNext(int* next, const string& s) {int j = 0;next[0] = 0;for(int i = 1; i < s.size(); i++) {while (j > 0 && s[i] != s[j]) {j = next[j - 1];}if (s[i] == s[j]) {j++;}next[i] = j;}}int strStr(string haystack, string needle) {if (needle.size() == 0) {return 0;}int next[needle.size()];getNext(next, needle);int j = 0;//使用next数据,将haystack与needle进行匹配。for (int i = 0; i < haystack.size(); i++) {while(j > 0 && haystack[i] != needle[j]) {j = next[j - 1];}if (haystack[i] == needle[j]) {j++;}if (j == needle.size() ) { // 文本串s里出现了模式串treturn (i - needle.size() + 1);}}return -1;}
};
- 时间复杂度: O(n + m)
- 空间复杂度: O(m)
多自己写几遍,就会理解的更深一点。
459.重复的子字符串
https://leetcode.cn/problems/repeated-substring-pattern/
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。
思考:最多由一半的子串组成。利用kmp算法不断找最小重复子串。
随想录:判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是由重复子串组成。当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,要刨除 s + s 的首字符和尾字符,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
class Solution {
public:bool repeatedSubstringPattern(string s) {string t = s + s;t.erase(t.begin());t.erase(t.end() - 1);if (t.find(s) != std::string::npos) return true;return false;}
};
- 时间复杂度: O(n)
- 空间复杂度: O(1)
kmp思路:
最长相等前后缀不包含的子串就是最小重复子串
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7OWiy2H8-1691982232465)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/df6b2f6b-6ed3-441d-9fee-ffe8dbba32ff/Untitled.png)]
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。
class Solution {
public:void getNext (int* next, const string& s){next[0] = 0;int j = 0;for(int i = 1;i < s.size(); i++){while(j > 0 && s[i] != s[j]) {j = next[j - 1];}if(s[i] == s[j]) {j++;}next[i] = j;}}bool repeatedSubstringPattern (string s) {if (s.size() == 0) {return false;}int next[s.size()];getNext(next, s);int len = s.size();if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {return true;}return false;}
};
- 时间复杂度: O(n)
- 空间复杂度: O(n)
字符串总结
1、C语言中,已结束符’\0’ 判断字符串是否结束。C++中,提供一个string类,string类会提供 size接口,可以用来判断string类字符串是否结束,就不用’\0’来判断是否结束。
2、那么vector< char > 和 string 又有什么区别呢?其实在基本操作上没有区别,但是 string提供更多的字符串处理的相关接口,例如string 重载了+,而vector却没有。所以想处理字符串,我们还是会定义一个string类型。
3、打基础的时候,不要太迷恋于库函数。
4、双指针法在数组,链表和字符串中很常用。其实很多数组填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
5、KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
复盘总结
个人反思
字符串类类型的题目,往往想法比较简单,但是实现起来并不容易,复杂的字符串题目非常考验对代码的掌控能力。
双指针法是字符串处理的常客。
KMP算法是字符串查找最重要的算法
相关文章:
、459.重复的子字符串)
day9 | 28. 实现 strStr()、459.重复的子字符串
目录: 解题及思路学习 28. 实现 strStr() https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/ 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下…...

hive on tez资源控制
sql insert overwrite table dwintdata.dw_f_da_enterprise2 select * from dwintdata.dw_f_da_enterprise; hdfs文件大小数量展示 注意这里文件数有17个 共计321M 最后是划分为了21个task 为什么会有21个task?不是128M 64M 或者说我这里小于128 每个文件一个map…...

企业有VR全景拍摄的需求吗?能带来哪些好处?
在传统图文和平面视频逐渐疲软的当下,企业商家如何做才能让远在千里之外的客户更深入、更直接的详细了解企业品牌和实力呢?千篇一律的纸质材料已经过时了,即使制作的再精美,大家也会审美疲劳;但是你让客户远隔千里&…...

【问题解决】Git命令行常见error及其解决方法
以下是我一段时间没有使用xshell,然后用git命令行遇到的一些系列错误和他们的解决方法 遇到了这个报错: fatal: Not a git repository (or any of the parent directories): .git 我查阅一些博客和资料,可以解决的方式: git in…...

【100天精通python】Day34:使用python操作数据库_ORM(SQLAlchemy)使用
目录 专栏导读 1 ORM 概述 2 SQLAlchemy 概述 3 ORM:SQLAlchemy使用 3.1 安装SQLAlchemy: 3.2 定义数据库模型类: 3.3 创建数据表: 3.4 插入数据: 3.5 查询数据: 3.6 更新数据: 3.7 删…...
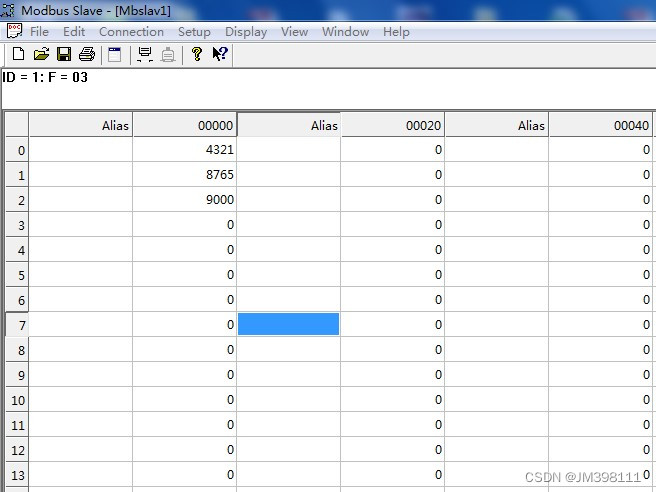
CCLINK IE转MODBUS-TCP网关modbus tcp协议详解
你是否曾经遇到过需要同时处理CCLINK IE FIELD BASIC和MODBUS两种数据协议的情况?捷米的JM-CCLKIE-TCP网关可以帮助你解决这个问题。 捷米JM-CCLKIE-TCP网关可以分别从CCLINK IE FIELD BASIC一侧和MODBUS一侧读写数据,然后将数据存入各自的缓冲区。接着…...

vue2根据不同的电脑分辨率显示页面内容及不同设备适配显示
1.安装插件: npm install postcss-px2rem px2rem-loader --save npm i lib-flexible --save 2.创建flexible.js,并在main.js引用 ;(function(win, lib) {var doc = win.document;var docEl = doc.documentElement;var metaEl = doc.querySelector(meta[name="viewport&…...

概率论:多维随机变量及分布
多维随机变量及分布 X X X为随机变量, ∀ x ∈ R , P { X ≤ x } F ( x ) \forall x\in R,P\{X\le x\}F(x) ∀x∈R,P{X≤x}F(x) 设 F ( x ) F(x) F(x)为 X X X的分布函数,则 (1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1 &am…...
flutter-第三方组件
卡片折叠 stacked_card_carousel 扫一扫组件 qr_code_scanner 权限处理组件 permission_handler 生成二维码组件 pretty_qr_code 角标组件 badges 动画组件 animations app更新 app_installer 带缓存的图片组件 cached_network_image 密码输入框 collection 图片保存 image_g…...
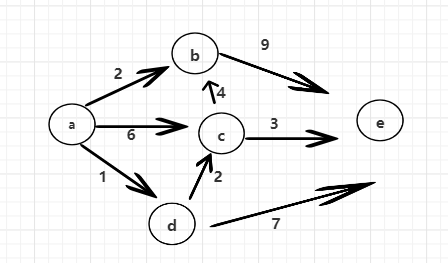
迪瑞克斯拉算法
迪锐克斯拉算法 简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。 所以说,迪…...
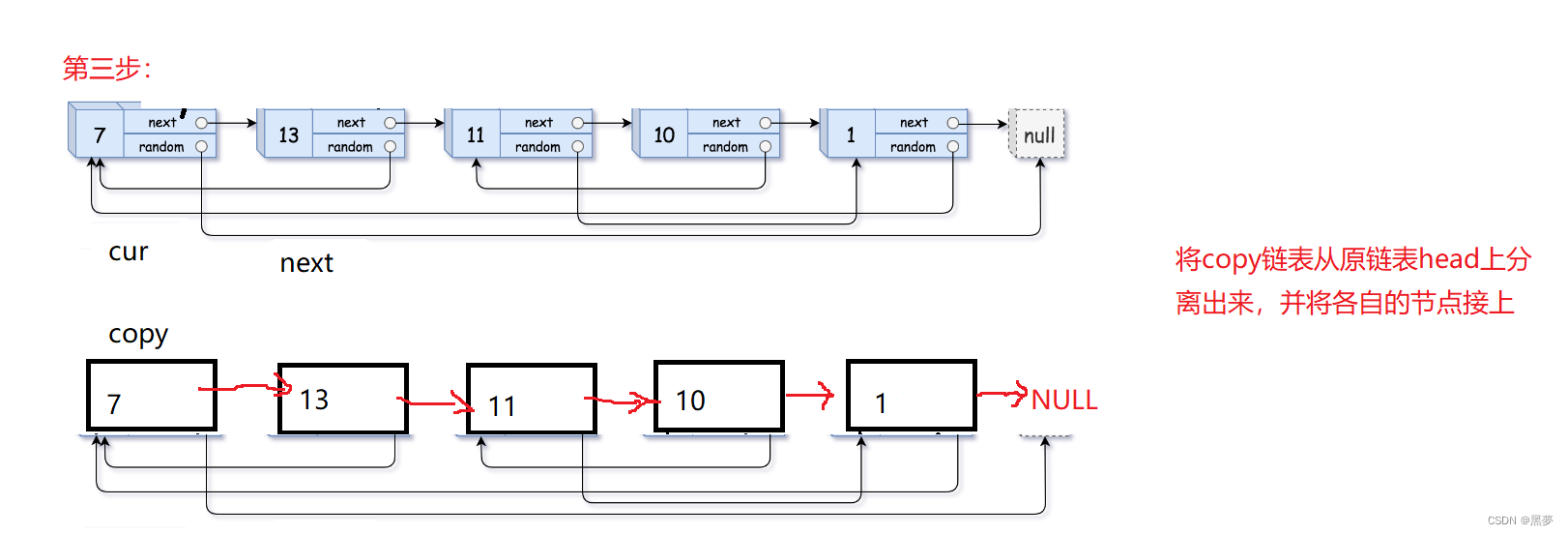
数据结构:力扣OJ题(每日一练)
目录 题一:环形链表 思路一: 题二:复制带随机指针的链表 思路一: 本人实力有限可能对一些地方解释的不够清晰,可以自己尝试读代码,望海涵! 题一:环形链表 给定一个链表的头节点…...

【论文阅读】基于深度学习的时序预测——Informer
系列文章链接 论文一:2020 Informer:长时序数据预测 论文二:2021 Autoformer:长序列数据预测 论文三:2022 FEDformer:长序列数据预测 论文四:2022 Non-Stationary Transformers:非平…...

机器学习 | Python实现GBDT梯度提升树模型设计
机器学习 | Python实现GBDT梯度提升树模型设计 目录 机器学习 | Python实现GBDT梯度提升树模型设计基本介绍模型描述模型使用参考资料基本介绍 机器学习 | Python实现GBDT梯度提升树模型设计。梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,GBDT也…...
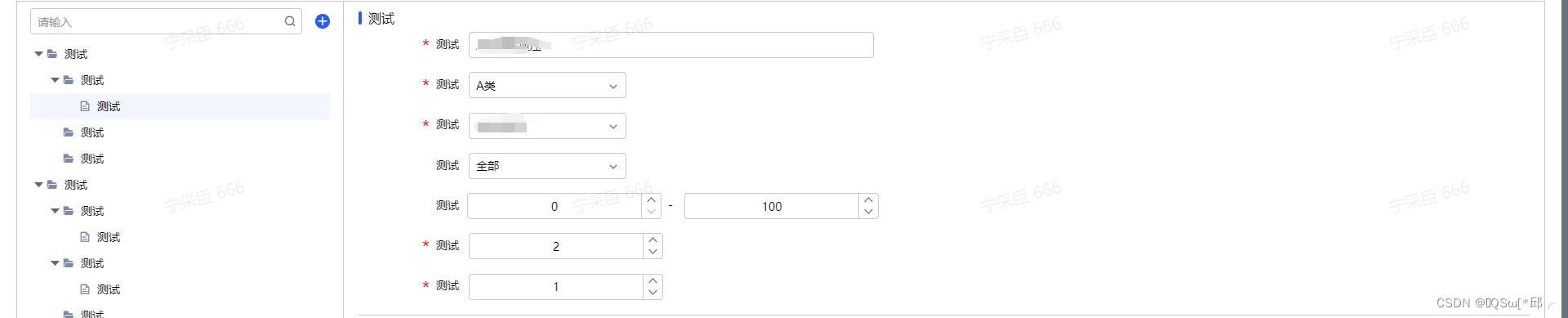
elementUi表单恢复至初始状态并不触发表单验证
elementUi表单恢复至初始状态并不触发表单验证 1.场景再现2.解决方法 1.场景再现 左侧是树形列表,右侧是显示节点的详情,点击按钮应该就是新增一个规则的意思,表单内容是没有改变的,所以就把需要把表单恢复至初始状态并不触发表单…...
大模型相关知识
一. embedding 简单来说,embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)…...

无法在 macOS Ventura 上启动 Multipass
异常信息 ➜ ~ sudo multipass authenticate Please enter passphrase: authenticate failed: Passphrase is not set. Please multipass set local.passphrase with a trusted client. ➜ ~ multipass set local.passphrase Please enter passphrase: Please re-enter…...

算法通关村第六关——原来如此简单
层次遍历:又叫广度优先遍历。就是从根节点开始,先访问根节点下面一层全部元素,再访问之后的层次,直到访问完二叉树的最后一层。 我们先看一下基础的层次遍历题,力扣102题:给你一个二叉树,请你返…...
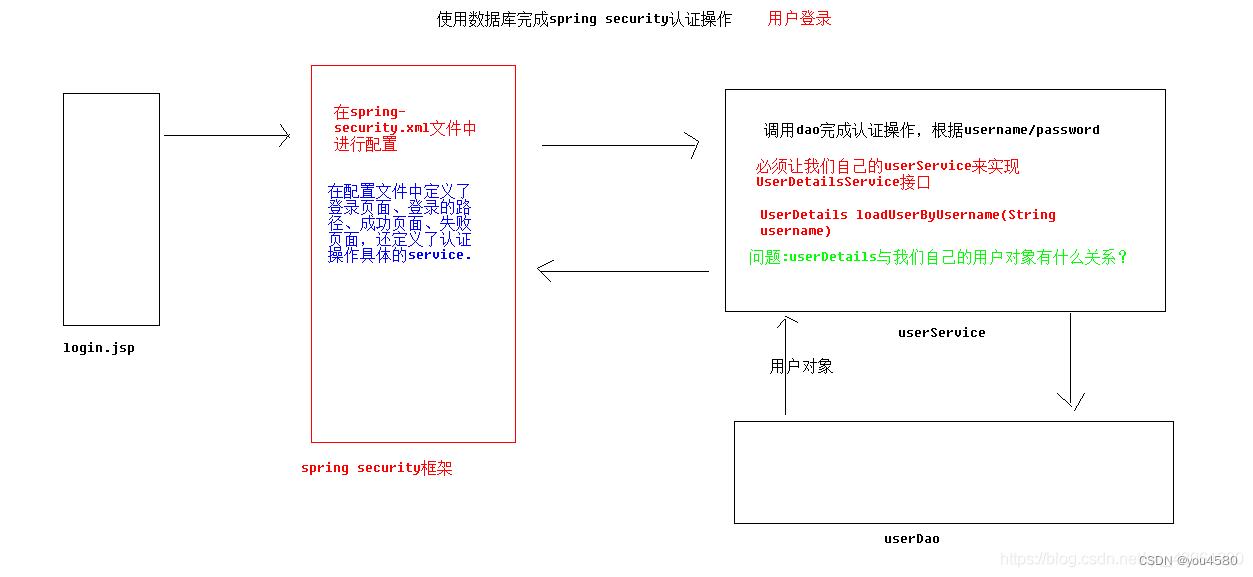
企业权限管理(八)-登陆使用数据库认证
Spring Security 使用数据库认证 在 Spring Security 中如果想要使用数据进行认证操作,有很多种操作方式,这里我们介绍使用 UserDetails 、 UserDetailsService来完成操作。 UserDetails public interface UserDetails extends Serializable { Collecti…...
第一百二十五天学习记录:C++提高:STL-deque容器(下)(黑马教学视频)
deque插入和删除 功能描述: 向deque容器中插入和删除数据 函数原型: 两端插入操作: push_back(elem); //在容器尾部添加一个数据 push_front(elem); //在容器头部插入一个数据 pop_back(); //删除容器最后一个数据 pop_front(); //删除容器…...

案例12 Spring MVC入门案例
网页输入http://localhost:8080/hello,浏览器展示“Hello Spring MVC”。 1. 创建项目 选择Maven快速构建web项目,项目名称为case12-springmvc01。 2.配置Maven依赖 <?xml version"1.0" encoding"UTF-8"?><project xm…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
