Windows - UWP - 网络不好的情况下安装(微软商店)MicrosoftStore的应用
Windows - UWP - 网络不好的情况下安装(微软商店)MicrosoftStore的应用
前言
UWP虽然几乎被微软抛弃了,但不得不否认UWP应用给用户带来的体验。沙箱的运行方式加上微软的审核,用户使用起来非常放心,并且完美契合Windows,资源占用非常小。
但是微软商店神奇的网络,使得安装过程十分看脸,经常出现下载失败的现象。
How
一、在微软商店网页版找到想要下载的应用
微软商店地址:apps.microsoft.com
可以在左侧搜索,之后点击今日应用页面。例如QQ音乐UWP
二、打开MS Generation Project下载“安装包”
MS Generation Project:store.rg-adguard.net
进入上述网站后,粘贴QQ音乐UWP的地址,点击“对号”搜索。
在出现的列表中,选择.appxbundle结尾或.appx结尾的文件,点击下载。
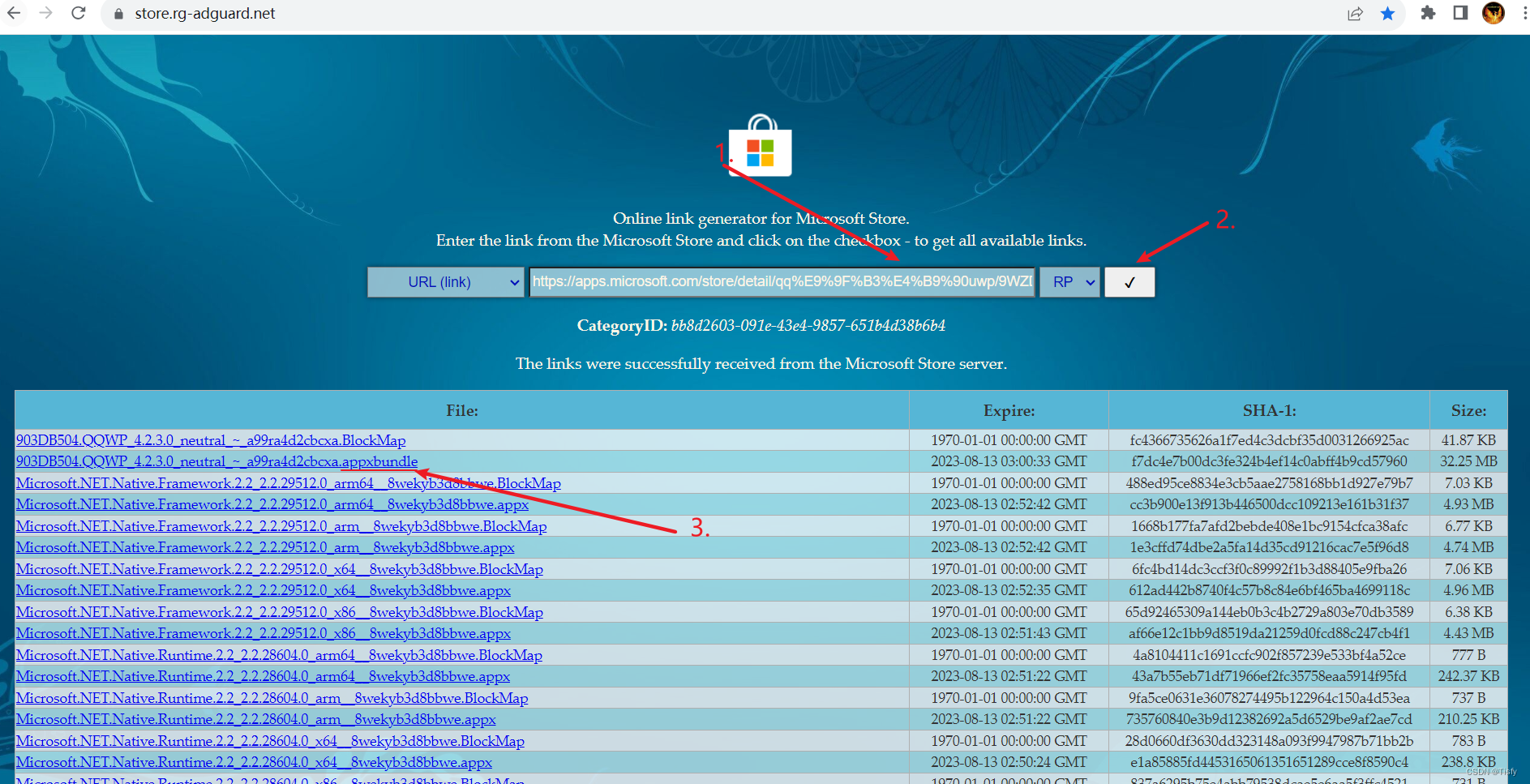
如果点击后没反应,可以试试右键 -> 复制连接地址,之后新建标签页 -> 输入地址。
这样下载速度可能还是很慢,但是既然是浏览器下载,就可以使用IDM等特殊手段了。
也可以使用我下载好的版本(不保证时效性,失效不补):AliyunDrive(阿里云盘禁止分享zip、appbundle格式的文件,单独修改后缀也不可以。因此我提取了QQ音乐UWP的图标,使用WinRAR制作了一个自解压文件,可以放心运行。运行后将会获得903DB504.QQWP_4.2.3.0_neutral_~_a99ra4d2cbcxa.AppxBundle。大概不会有人去下载吧QAQ)
三、安装
下载完成后,双击就可以安装了。
More
文件
我下载的文件是903DB504.QQWP_4.2.3.0_neutral_~_a99ra4d2cbcxa.AppxBundle,默认安装位置C:\Program Files\WindowsApps\903DB504.QQWP_4.2.3.0_x64__a99ra4d2cbcxa,默认缓存位置是C:\Users\LetMe\AppData\Local\Packages\903DB504.QQWP_a99ra4d2cbcxa
我对QQ音乐UWP的评价
我在微软商店给了个5⭐好评hh
虽然与win32相比少了很多功能,也存在很多BUG,但是系统开销是真的小,界面也算美观,虽然成本可能很高,但还是很支持腾讯开发QQ音乐的UWP[Doge]。
参考
原创不易,转载经作者同意后请附上原文链接哦~
https://letmefly.blog.csdn.net/article/details/132257018
相关文章:

Windows - UWP - 网络不好的情况下安装(微软商店)MicrosoftStore的应用
Windows - UWP - 网络不好的情况下安装(微软商店)MicrosoftStore的应用 前言 UWP虽然几乎被微软抛弃了,但不得不否认UWP应用给用户带来的体验。沙箱的运行方式加上微软的审核,用户使用起来非常放心,并且完美契合Wind…...

1040:输出绝对值
【题目描述】 输入一个浮点数,输出这个浮点数的绝对值,保留到小数点后两位。 【输入】 输入一个浮点数,其绝对值不超过10000。 【输出】 输出这个浮点数的绝对值,保留到小数点后两位。 【输入样例】 -3.14 【输出样例】 …...

[Docker精进篇] Docker部署和实践 (二)
前言: Docker部署是通过使用Docker容器技术,将应用程序及其所有相关依赖项打包为一个可移植、自包含的镜像,然后在任何支持Docker的环境中快速部署和运行应用程序的过程。 文章目录 Docker部署1️⃣为什么需要?2️⃣有什么作用&am…...
、459.重复的子字符串)
day9 | 28. 实现 strStr()、459.重复的子字符串
目录: 解题及思路学习 28. 实现 strStr() https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/ 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下…...

hive on tez资源控制
sql insert overwrite table dwintdata.dw_f_da_enterprise2 select * from dwintdata.dw_f_da_enterprise; hdfs文件大小数量展示 注意这里文件数有17个 共计321M 最后是划分为了21个task 为什么会有21个task?不是128M 64M 或者说我这里小于128 每个文件一个map…...

企业有VR全景拍摄的需求吗?能带来哪些好处?
在传统图文和平面视频逐渐疲软的当下,企业商家如何做才能让远在千里之外的客户更深入、更直接的详细了解企业品牌和实力呢?千篇一律的纸质材料已经过时了,即使制作的再精美,大家也会审美疲劳;但是你让客户远隔千里&…...

【问题解决】Git命令行常见error及其解决方法
以下是我一段时间没有使用xshell,然后用git命令行遇到的一些系列错误和他们的解决方法 遇到了这个报错: fatal: Not a git repository (or any of the parent directories): .git 我查阅一些博客和资料,可以解决的方式: git in…...

【100天精通python】Day34:使用python操作数据库_ORM(SQLAlchemy)使用
目录 专栏导读 1 ORM 概述 2 SQLAlchemy 概述 3 ORM:SQLAlchemy使用 3.1 安装SQLAlchemy: 3.2 定义数据库模型类: 3.3 创建数据表: 3.4 插入数据: 3.5 查询数据: 3.6 更新数据: 3.7 删…...
CCLINK IE转MODBUS-TCP网关modbus tcp协议详解
你是否曾经遇到过需要同时处理CCLINK IE FIELD BASIC和MODBUS两种数据协议的情况?捷米的JM-CCLKIE-TCP网关可以帮助你解决这个问题。 捷米JM-CCLKIE-TCP网关可以分别从CCLINK IE FIELD BASIC一侧和MODBUS一侧读写数据,然后将数据存入各自的缓冲区。接着…...

vue2根据不同的电脑分辨率显示页面内容及不同设备适配显示
1.安装插件: npm install postcss-px2rem px2rem-loader --save npm i lib-flexible --save 2.创建flexible.js,并在main.js引用 ;(function(win, lib) {var doc = win.document;var docEl = doc.documentElement;var metaEl = doc.querySelector(meta[name="viewport&…...

概率论:多维随机变量及分布
多维随机变量及分布 X X X为随机变量, ∀ x ∈ R , P { X ≤ x } F ( x ) \forall x\in R,P\{X\le x\}F(x) ∀x∈R,P{X≤x}F(x) 设 F ( x ) F(x) F(x)为 X X X的分布函数,则 (1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1 &am…...
flutter-第三方组件
卡片折叠 stacked_card_carousel 扫一扫组件 qr_code_scanner 权限处理组件 permission_handler 生成二维码组件 pretty_qr_code 角标组件 badges 动画组件 animations app更新 app_installer 带缓存的图片组件 cached_network_image 密码输入框 collection 图片保存 image_g…...
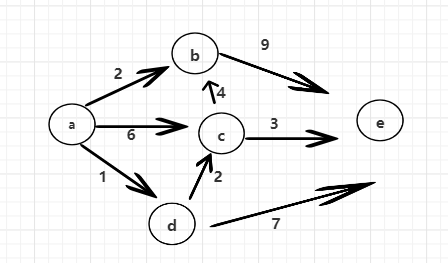
迪瑞克斯拉算法
迪锐克斯拉算法 简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。 所以说,迪…...
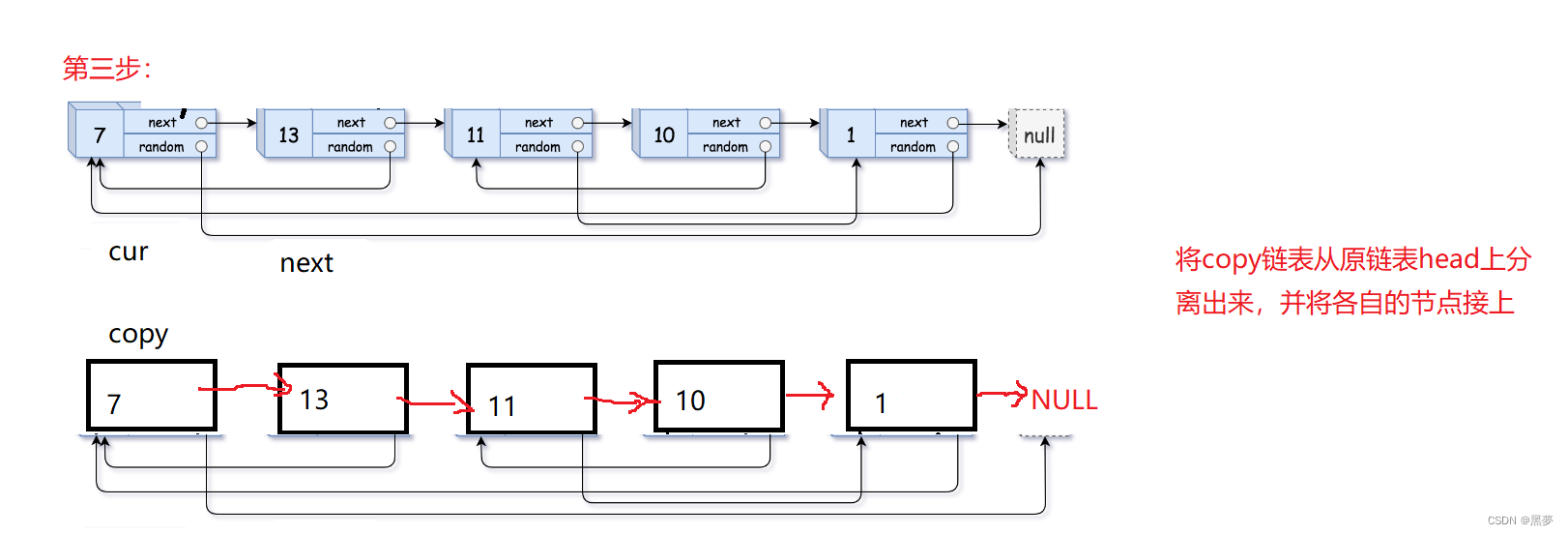
数据结构:力扣OJ题(每日一练)
目录 题一:环形链表 思路一: 题二:复制带随机指针的链表 思路一: 本人实力有限可能对一些地方解释的不够清晰,可以自己尝试读代码,望海涵! 题一:环形链表 给定一个链表的头节点…...

【论文阅读】基于深度学习的时序预测——Informer
系列文章链接 论文一:2020 Informer:长时序数据预测 论文二:2021 Autoformer:长序列数据预测 论文三:2022 FEDformer:长序列数据预测 论文四:2022 Non-Stationary Transformers:非平…...

机器学习 | Python实现GBDT梯度提升树模型设计
机器学习 | Python实现GBDT梯度提升树模型设计 目录 机器学习 | Python实现GBDT梯度提升树模型设计基本介绍模型描述模型使用参考资料基本介绍 机器学习 | Python实现GBDT梯度提升树模型设计。梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,GBDT也…...
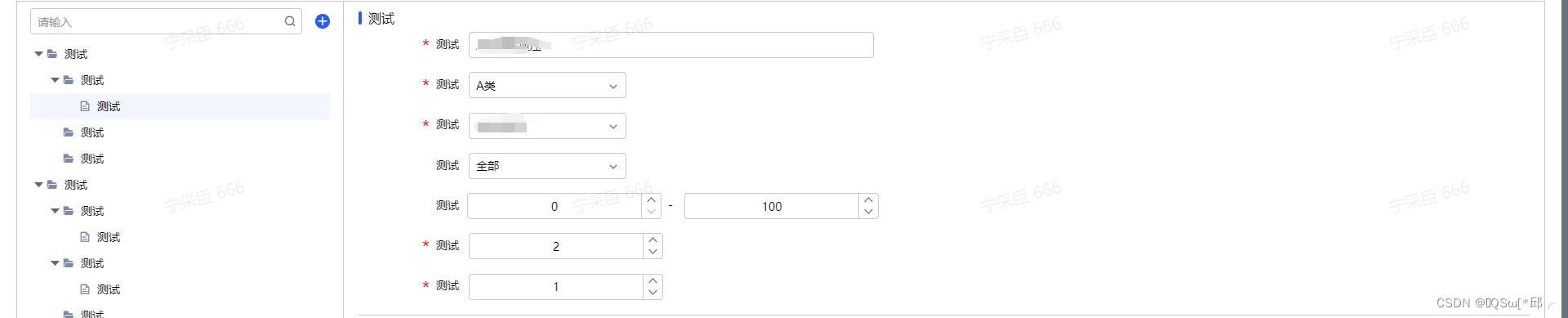
elementUi表单恢复至初始状态并不触发表单验证
elementUi表单恢复至初始状态并不触发表单验证 1.场景再现2.解决方法 1.场景再现 左侧是树形列表,右侧是显示节点的详情,点击按钮应该就是新增一个规则的意思,表单内容是没有改变的,所以就把需要把表单恢复至初始状态并不触发表单…...
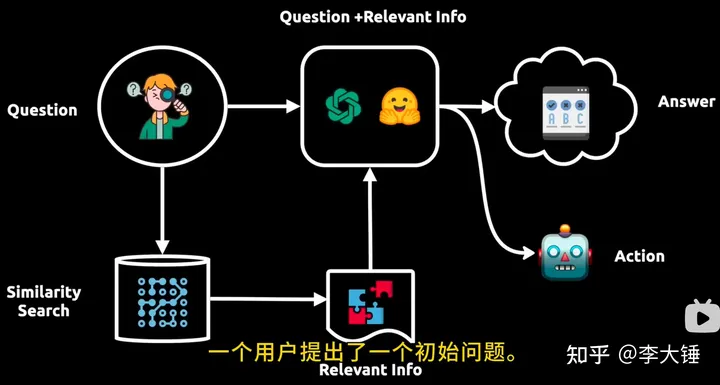
大模型相关知识
一. embedding 简单来说,embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)…...

无法在 macOS Ventura 上启动 Multipass
异常信息 ➜ ~ sudo multipass authenticate Please enter passphrase: authenticate failed: Passphrase is not set. Please multipass set local.passphrase with a trusted client. ➜ ~ multipass set local.passphrase Please enter passphrase: Please re-enter…...

算法通关村第六关——原来如此简单
层次遍历:又叫广度优先遍历。就是从根节点开始,先访问根节点下面一层全部元素,再访问之后的层次,直到访问完二叉树的最后一层。 我们先看一下基础的层次遍历题,力扣102题:给你一个二叉树,请你返…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
