对约瑟夫问题的进一步思考
- 约瑟夫问题重述:
在计算机编程的算法中,类似问题又称为约瑟夫环
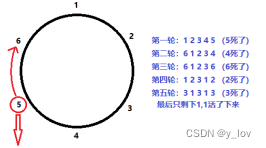
约瑟夫环:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。
例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3,1。
如图所示
2.约瑟夫问题递归法计算原理:
2.1 内容:设F(N,M)为最后存活者的位置(位置从0开始),则有:
F(N,M)=(F(N-1,M)+M)%N
2.2 证明:数学归纳法
· 当n=1时,f(1,m)=0,因为编号从0开始且只有一个人,胜利者编号显然为0。 当n=2时,序列为0,1,若m为奇数,则胜利者编号为1;若m为偶数,则胜利者编号为0,易有f(2,m)=m%2=(0+m)%2=[f(1,m)+m]%2,结论成立。
· 假设当n=i-1时结论成立,即对于序列0,1,2,...,i-2而言,最后的胜利者编号为f(i-1,m)。 当n=i时,序列为0,1,2,...,i-1。设第一轮的淘汰者编号为k(若m%i=0,则k=i-1,否则k=m%i-1),则序列可表示为0,1,2,...,k-1,k,k+1,...,i-1。第一轮淘汰k,余下的序列x'为k+1,...,i-1,0,1,...,k-1,问题规模变为i-1。 因为由归纳假设,当n=i-1时,对于序列x:0,1,2,...,f(i-1,m),...,i-2,胜利者编号为f(i-1,m)。
由于x'=(x+k+1)%i,故f(i,m)=[f(i-1,m)+k+1]%i。当m%i=0时,k+1=i,[f(i-1,m)+k+1]%i=[f(i-1,m)+i]%i=f(i-1,m)%i+0=f(i-1,m)%i+m%i=[f(i-1,m)+m]%i;当m%i!=0时,k+1=m%i,[f(i-1,m)+k+1]%i=[f(i-1,m)+m%i]%i=[f(i-1,m)+m]%i。故当n=i时,结论成立。
· 综上,命题成立。
3.设计对象问题:
3.1问题重述:
假设你正在游玩约瑟夫游戏,从你开始报数,游戏规则与课上讲述一致,现在你想确保你是最后一个出列的玩家,如果由你设置m(即每报几个数出列一人),你应该如何设置m来确保自己的胜利?
3.2问题分析:
- F(N,M)=(F(N-1,M)+M)%N
- 设“我”的编号为S,总人数为N,每次第M个人被杀掉,S,N为已知量,M是待确定量;
- 最终目标:在保证F(N,M)+ S = S的条件下,确定M;
- 在确保时间复杂度,计算的开销等因素下,尽量进行优化的选取。
3.3问题求解:
F(N , M) = (F(N-1,M)+M) mod N (1)
F(N , M) = 0; ( 2 )
思路1:枚举法
1.实现:枚举m,运用公式计算F(N,M) , 找到满足条件的m;
2.复杂度:O(n*m);
3.优点: 思路简单,枚举足够多就能找到全部解,且容易。
4.缺点:用while()枚举,当大到一定程度终结。无法确定是否能找到m,以及m要枚举多大。
思路2:设计法
- 实现:
F(1,M) = 0;
F(2,M) = (M)%2 = 0;
F(3,M) = (M%2 +M)%3 = 0 ;
...
F(N,M) = (M%2 + M%3 + M%4 +...+M%N)%N = 0;
令 M = N!,则满足条件。
2.复杂度:O(N);
3.优点: 复杂度低
4.缺点:当N过大时,m数据值过大。
6.优化
1.操作:
双指针删因子法缩小m规模。
试图在不改变复杂度条件下删除公共因子以减小m的数据规模。
- 复杂度: O(N);
- 缺陷:降低规模效果不明显,依旧只能处理小范围数据
- 进一步优化:
- 方法1:用string进行大数计算;
- 方法2:用Python;
- 方法3:n小则用法2,n大用法1,但是依旧具有m不确定是否能找到的不稳定性。
只需在原有基础上修改为大数模式,在此除了方法三外不做具体实现。
相关文章:

对约瑟夫问题的进一步思考
约瑟夫问题重述: 在计算机编程的算法中,类似问题又称为约瑟夫环 约瑟夫环:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。 例如N6,M5࿰…...

程序员如何优雅的提升软件开发效率?
一、前言 面对日益发达的,极具诱惑力的夜生活,很少有人能置身事外。 但是有那么一群人,即使黑幕高垂还坚守在工作之位,无视夜晚的繁荣和喧嚣。 是的,他们就是程序员,一群成天编写代码的程序员。 相信&#…...

宽屏企业网站介绍
宽屏企业网站是一种以宽屏设计为特点的网站,旨在提供更丰富、精美的网页展示效果,适合于展示企业的品牌形象、产品介绍和服务内容。该类网站常用于企业展示、商务推广、企业形象塑造等场景。 宽屏企业网站的内容介绍一般包括以下几个方面: 公…...
OPENCV C++(八)HOG的实现
hog适合做行人的识别和车辆识别 对一定区域的形状描述方法 可以表示较大的形状 把图像分成一个一个小的区域的直方图 用cell做单位做直方图 计算各个像素的梯度强度和方向 用3*3的像素组成一个cell 3*3的cell组成一个block来归一化 提高亮度不变性 常用SVM分类器一起使用…...
干货分享:制作婚礼请柬的技巧,从零基础起步
在现代社会,婚礼请柬已经成为了婚礼必备的一部分。而如何制作一个个性化的婚礼请柬呢?今天,我们将分享一个简便而可靠的制作方法,那就是使用乔拓云平台。 乔拓云平台是一个可靠的第三方制作工具,提供了丰富的H5模板&am…...
c语言每日一练(6)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,暑假时三天之内必有一更,到了开学之后,将看学业情…...

2023年国赛数学建模思路 - 复盘:校园消费行为分析
文章目录 0 赛题思路1 赛题背景2 分析目标3 数据说明4 数据预处理5 数据分析5.1 食堂就餐行为分析5.2 学生消费行为分析 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 赛题背景 校园一卡通是集…...

WebAPIs 第四天
1.日期对象 2.节点操作 3.M端事件 4.JS插件 一.日期对象 实例化时间对象方法时间戳 日期对象:用来表示时间的对象 作用:可以得到当前系统时间 1.1 实例化 ① 概念:在代码中发现了new关键字时,一般将这个操作称为实例化 …...

SQL 语句解析过程详解
SQL 语句解析过程详解: 1.输入SQL语句 2.词法分析------flex 使用词法分析器(由Flex生成)将 SQL 语句分解为一个个单词,这些单词被称为“标记“。标记包括关键字、标识符、运算符、分隔符等。 2.1 flex 原…...

单源最短路径【学习算法】
单源最短路径【学习算法】 前言版权推荐单源最短路径Java算法实现代码结果 带限制的单源最短路径1928. 规定时间内到达终点的最小花费LCP 35. 电动车游城市 最后 前言 2023-8-14 18:21:41 以下内容源自《【学习算法】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此…...
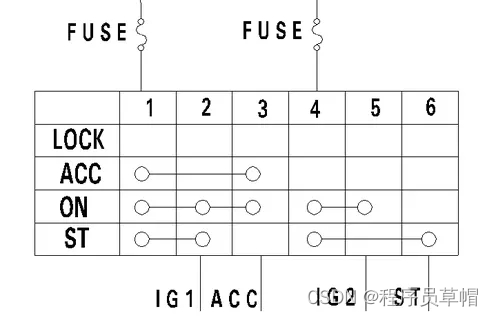
汽车上的电源模式详解
① 一般根据钥匙孔开关的位置来确定整车用电类别,汽车上电源可以分为常电,IG电,ACC电 1)常电。常电表示蓄电池和发电机输出直接供电,即使点火开关在OFF档时,也有电量供应。一般来讲模块的记忆电源及需要在车…...

【碎碎念随笔】1、回顾我的电脑和编程经历
✏️ 闲着无事,讲述一下我的计算机和代码故事 一、初识计算机 🖥️ 余家贫,耕植无钱买电脑。大约六年级暑假,我在姐姐哪儿第一次接触到了计算机(姐姐也是买的二手)。 🖥️ 计算机真有趣&#x…...
)
背上花里胡哨的书包准备面试之webpack篇(+一些常问的面试题)
目录 webpack理解? webpack构建流程? loader解决什么问题? plugin解决什么问题? 编写loader和plugin的思路? webpack热更新? 如何提高webpack的构建速度? 问git常用命令? ht…...

你知道什么是Curriculum Training模型吗
随着深度学习技术的飞速发展,研究人员在不断探索新的训练方法和策略,以提高模型的性能和泛化能力。其中,Curriculum Training(课程学习)模型作为一种前沿的训练方法,引起了广泛的关注和研究。本文将深入探讨…...

vue 大文件视频切片上传处理方法
前端上传大文件、视频的时候会出现超时、过大、很慢等情况,为了解决这一问题,跟后端配合做了一个切片的功能。 我这个切片功能是基于 minion 的,后端会把文件放在minion服务器上。具体看后端怎么做 1、在项目的 util(这个文件夹是自己创建的…...
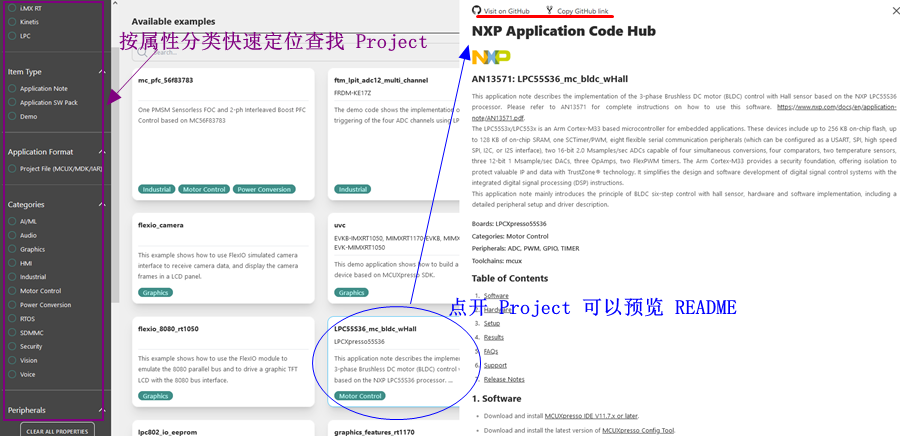
痞子衡嵌入式:AppCodeHub - 一站网罗恩智浦MCU应用程序
近日,恩智浦官方隆重上线了应用程序代码中心(Application Code Hub,简称 ACH),这是恩智浦 MCUXpresso 软件生态的一个重要组成部分。痞子衡之所以要如此激动地告诉大家这个好消息,是因为 ACH 并不是又一个恩智浦官方 github proje…...
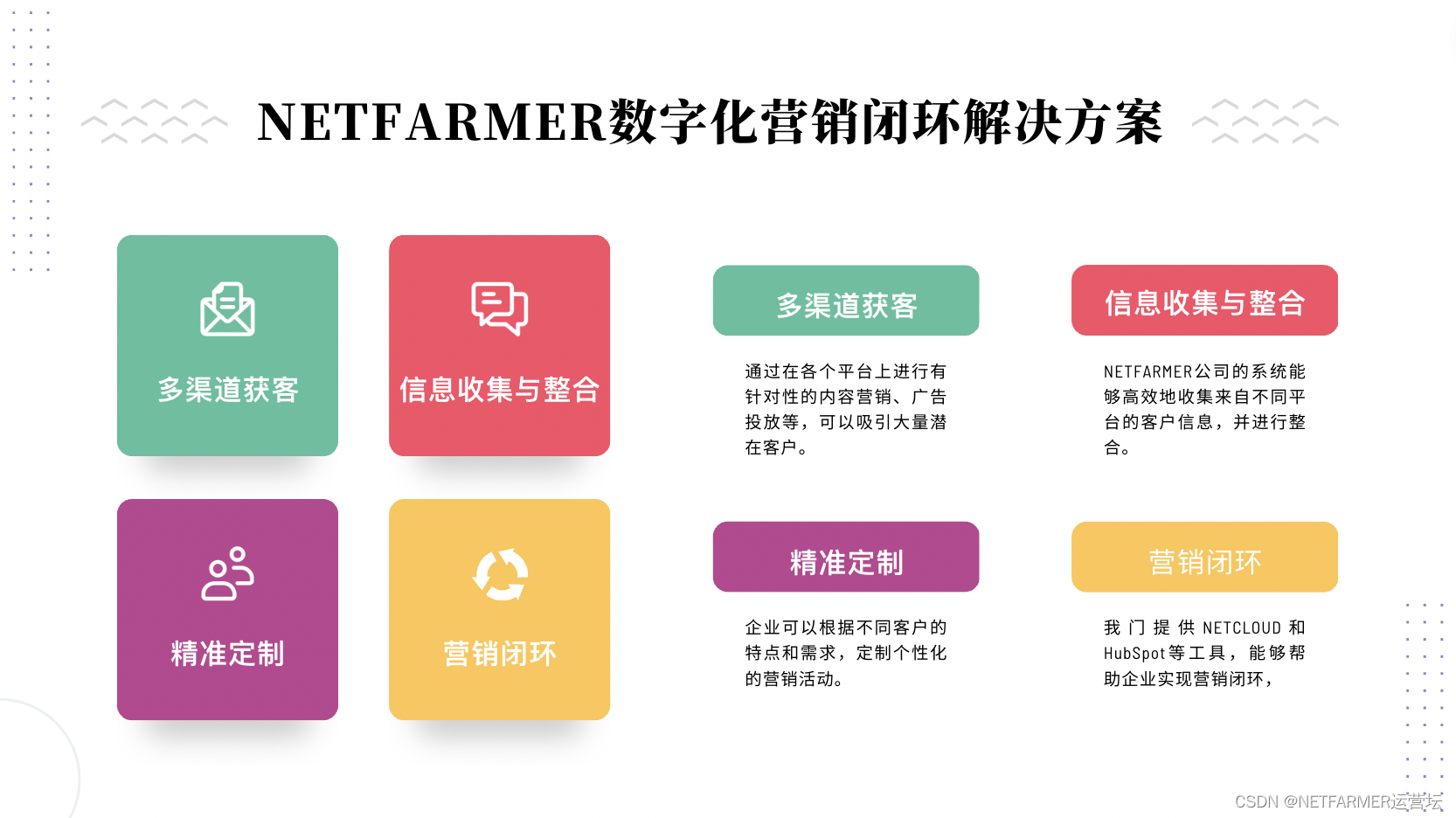
打造数字化营销闭环,破解精准获客难题
现阶段,企业需要进行数字化营销闭环,以实现更精确的客户获取。随着数字技术的迅猛发展,企业需要将在线广告、社交媒体营销和数据分析等工具相互结合,建立一个完整的数字化营销流程。通过使用客户细分、精准定位和个性化广告等手段…...
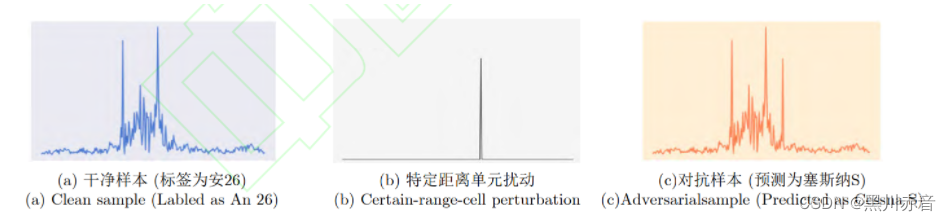
《雷达像智能识别对抗研究进展》阅读记录
(1)引言 神经网络通常存在鲁棒性缺陷,易受到对抗攻击的威胁。攻击者可以隐蔽的诱导雷达智能目标识别做出错误预测,如: a图是自行车,加上对抗扰动后神经网络就会将其识别为挖掘机。 (2&a…...
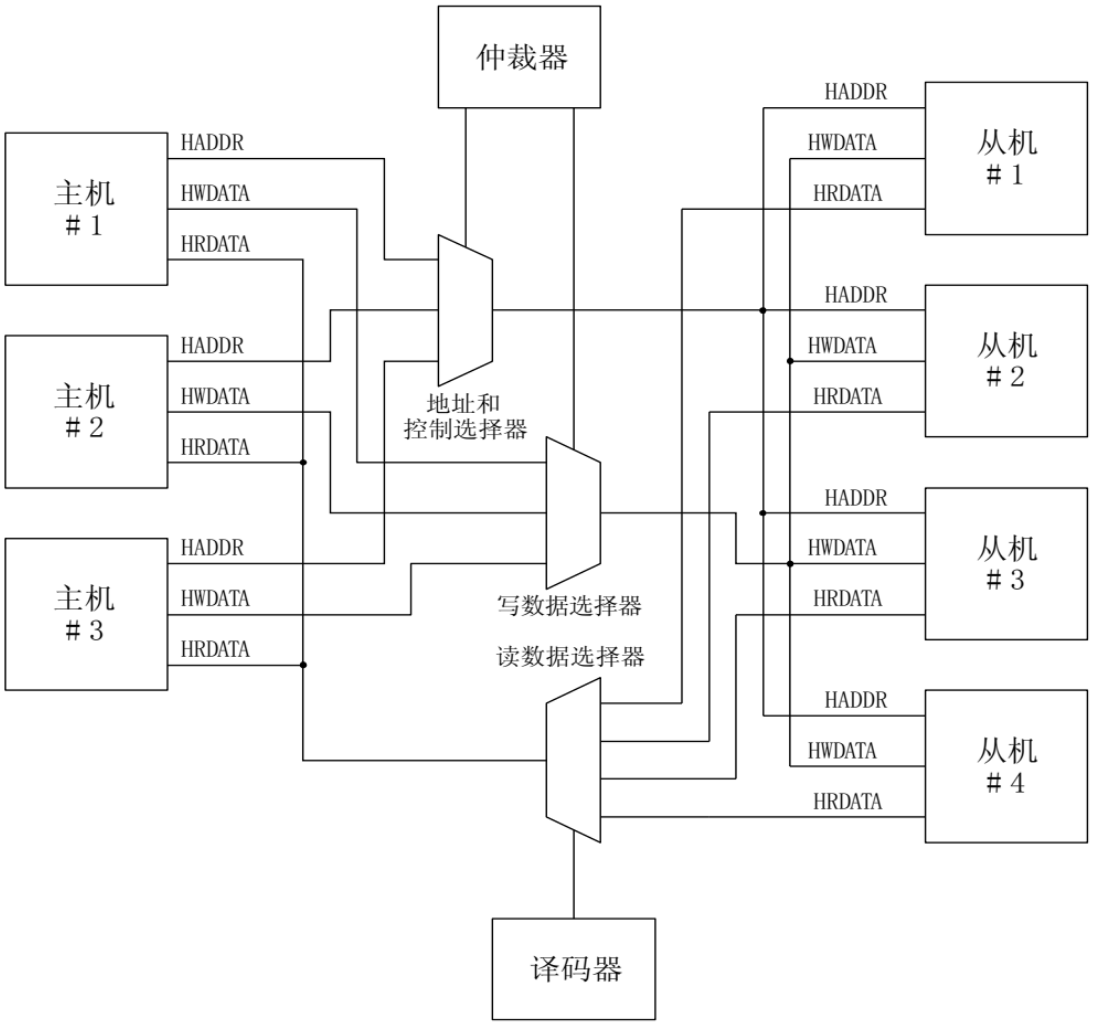
【AHB】初识 AHB 总线
AHB 与 APB、ASB同属于 AMBA 总线架构规范,该总线规范由 ARM 公司提出。 目录 一、AHB 总线 二、AHB 总线组成 三、AHB 主从通信过程 一、AHB 总线 AHB(Advanced High Performance Bus),意为高级高性能总线,能将微控制器&…...

Linux服务使用宝塔面板搭建网站,通过内网穿透实现公网访问
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
