C语言刷题训练【第11天】
大家好,我是纪宁。
今天是C语言笔试刷题训练的第11天,加油!
文章目录
- 1、声明以下变量,则表达式: ch/i + (f*d – i) 的结果类型为( )
- 2、关于代码的说法正确的是( )
- 3、已知有如下各变量的类型说明,则以下不符合C语言语法的表达式是( )
- 4、下面函数的输出结果是( )
- 5、如下代码的输出结果是( )
- 最大连续 1 的个数
- 完全数计算(完数)
1、声明以下变量,则表达式: ch/i + (f*d – i) 的结果类型为( )
char ch;
int i;
float f;
double d;
A: char B: int C: float D: double
基本数据类型的等级从低到高如下:char int long float double运算的时候是从低转到高的,表达式的类型会自动提升或者转
换为参与表达式求值的最上级类型,所以选D
2、关于代码的说法正确的是( )
#include <stdio.h>
int main()
{int x = -1;unsigned int y = 2;if (x > y){printf("x is greater");}else{printf("y is greater");}return 0;
}
A: x is greater B: y is greater C: 依赖实现 D: 随机
x是有符号数-1,内存中是全1,当有符号的x和无符号数进行比较时,x会隐式类型转换被当做无符号数,是一个很大的数,
这时就选择A了
3、已知有如下各变量的类型说明,则以下不符合C语言语法的表达式是( )
int k, a, b;
unsigned int w = 5;
double x = 1.42;
A: x%3 B: w+=-20 C: k=(a=200,b=300) D: a+=a-=a=9
取余操作两边必须是整数,所以选A
4、下面函数的输出结果是( )
void func()
{
int k = 1^(1 << 31 >> 31);printf("%d\n", k);
}
A: 0 B: -1 C: -2 D: 1
(1 << 31 );左移31位,并在右侧填充0,得到0x80000000,即符号位为1,其他为0,即-2147483648
int k = 1^(1 << 31 >> 31);注意,这里在右移的时候,符号位保持为1,右移后填充1,结果为0xFFFFFFFF,即-1,
0x00000001^0xFFFFFFFF,即0xFFFFFFFE(-2),所以选D

5、如下代码的输出结果是( )
#include <stdio.h>
int main()
{int i = 1;sizeof(i++);printf("%d\n", i);return 0;
}
A: 1 B: 4 C: 2 D: 8
一般表达式的运算是在运行时执行的,而sizeof是一个编译阶段就执行的运算符,在其内的任何运算都不执行,只推测出其中
表达式结果的类型求其大小,故前后i的值不变,所以选A=
最大连续 1 的个数
给定一个二进制数组 nums , 计算其中最大连续 1 的个数。

int findMaxConsecutiveOnes(int* nums, int numsSize){int max=0,count=0;max=count;int*p=nums;while(numsSize--){if(*p==1){count++;p++;}else if(*p==0){count=0;p++;}if(count>max)max=count;}return max;
}
这道题思路比较简单,统计连续1的个数,遇到0时表示连续中断,判断如果当前的统计数大于之前最大的则替换,然后继续下一个位置开始的统计即可。要注意最后一个数组元素的判断,很容易会将最后一个数组元素略过。
完全数计算(完数)
完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。
它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。
例如:28,它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加,1+2+4+7+14=28。
输入n,请输出n以内(含n)完全数的个数。
输入描述:输入一个数字n
输出描述:输出不超过n的完全数的个数
#include<math.h>
#include <stdio.h>
int main(){int n = 0, count = 0, ret = 1;scanf("%d", &n);do{for (int i = 2; i <=sqrt(n); i++){if (n % i == 0){ret += i;if(i!=n/i)ret += n / i;}}if (ret == n)count++;ret = 1;} while (--n);printf("%d", count-1);
}
这道题的关键在于完全数的判断:完全数指的是一个数字的所有约数的和和自身相等。我们只需要从 1 开始将这个数的约数相加求和即可。
约数就是能够被数字整除,而这里简化的一个思路是数字能够被整除,则除数和结果就都是约数,这种思路下,只需要从1计算到平方根即可。
比如:数字 8 , 能够整除 2 ,结果是 4 ,则除数 2 和结果 4 都是约数,而这两个只需要一次计算判断即可。需要注意的是 4,9,25… 这种,除数和结果相同的情况,则除数或者结果只相加一次就够了。
而这段代码其实是将1也算进去了,所以最后总数减1。

相关文章:

C语言刷题训练【第11天】
大家好,我是纪宁。 今天是C语言笔试刷题训练的第11天,加油! 文章目录 1、声明以下变量,则表达式: ch/i (f*d – i) 的结果类型为( )2、关于代码的说法正确的是( )3、已知有如下各变…...

正则表达式的使用
1、正则表达式-教程 正则表达式:文本模式,包括普通字符(例如,a到z之间的字母)和特殊字符(称为元字符)。 正则表达式使用单个字符串来描述,匹配一系列匹配某个句法规则的字符串。 2、…...

PHP 求解两字符串所有公共子序列及最长公共子序列 支持多字节字符串
/*** 获取两字符串所有公共子序列【不连续的】 例:abc ac > ac** param string $str1 字符串1* param string $str2 字符串2** return array*/ function public_sequence(string $str1, string $str2): array {$data [[-1, -1, , 0, ]]; // 子序列容器【横坐标 …...

linux内核bitmap之setbit汇编实现
内核版本:kernel 0.12 首先看一段代码,下面这段代码来自内核版本0.12的mm/swap.c中: // mm/swap.c #define bitop(name,op) \static inline int name(char * addr,unsigned int nr) \ { \int __res; \__asm__ __volatile__("bt" …...

Golang设计模式
Golang设计模式 Golang设计模式简介Golang工厂设计模式Golang单例设计模式Golang抽象工厂设计模式Golang建造者模式 (Builder Pattern)Golang 原型模式(Prototype Pattern)Golang适配器模式Golang 桥接模式(Bridge Pattern)Golang装饰器模式(Decorator …...

leetcode151. 反转字符串中的单词
题目:leetcode151. 反转字符串中的单词 描述: 给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结…...

【BASH】回顾与知识点梳理(十七)
【BASH】回顾与知识点梳理 十七 十七. 什么是 Shell scripts17.1 干嘛学习 shell scripts自动化管理的重要依据追踪与管理系统的重要工作简单入侵检测功能连续指令单一化简易的数据处理跨平台支持与学习历程较短 17.2 第一支 script 的撰写与执行撰写第一支 script 17.3 撰写 s…...
时序预测-Informer简介
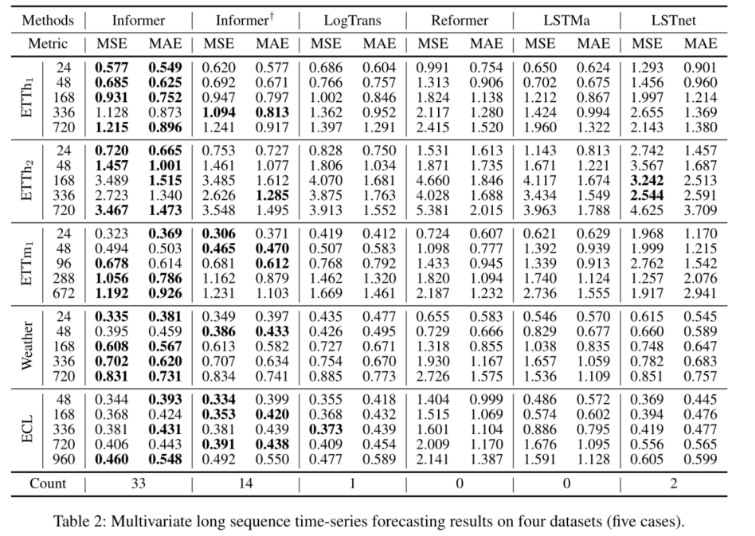
文章目录 Informer介绍1. Transformer存在的问题2. Informer研究背景3. Informer 整体架构3.1 ProbSparse Self-attention3.2 Self-attention Distilling3.3 Generative Style Decoder 4. Informer的实验性能5. 相关资料 Informer介绍 1. Transformer存在的问题 Informer实质…...

2023牛客第七场补题报告C F L M
2023牛客第七场补题报告C F L M C-Beautiful Sequence_2023牛客暑期多校训练营7 (nowcoder.com) 思路 观察到数组一定是递增的,所以从最高位往下考虑每位的1最多只有一个,然后按位枚举贪心即可。 代码 #include <bits/stdc.h> using namespac…...
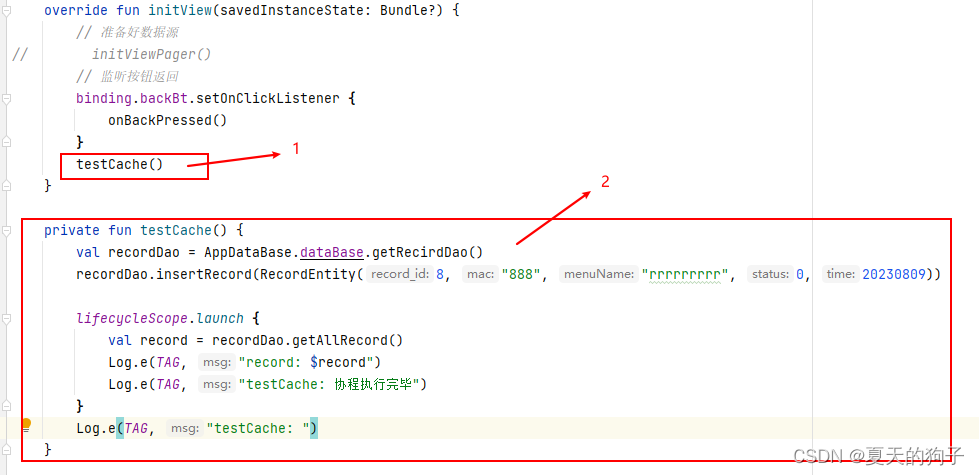
Android使用kotlin+协程+room数据库的简单应用
前言:一般主线程(UI线程)中是不能执行创建数据这些操作的,因为等待时间长。所以协程就是为了解决这个问题出现。 第一步:在模块级的build.gradle中引入 id com.android.application// roomid kotlin-androidid kotlin…...
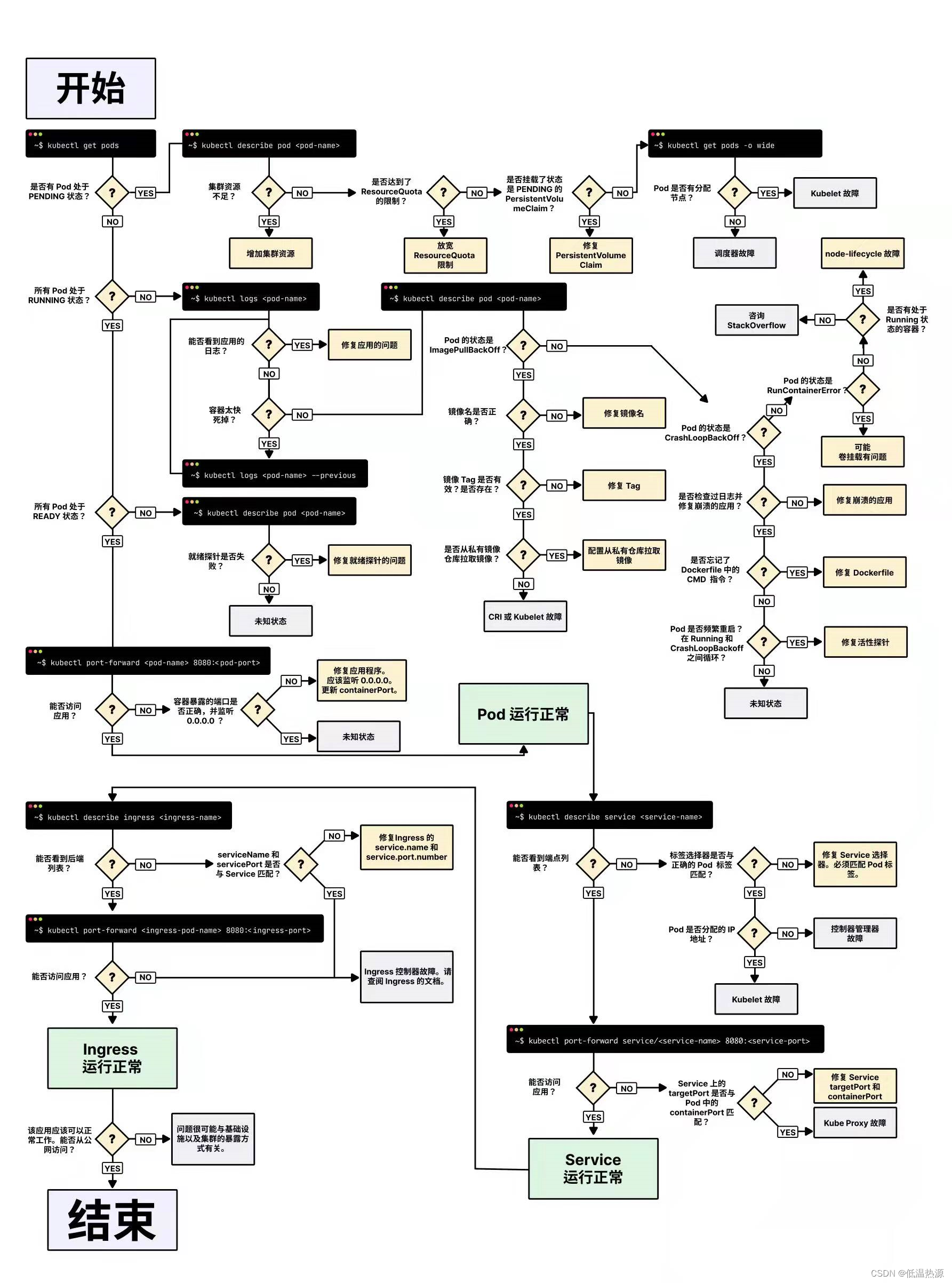
Kubernetes pod调度约束[亲和性 污点] 生命阶段 排障手段
调度约束 Kubernetes 是通过 List-Watch 的机制进行每个组件的协作,保持数据同步的,每个组件之间的设计实现了解耦。 用户是通过 kubectl 根据配置文件,向 APIServer 发送命令,在 Node 节点上面建立 Pod 和 Container。 APIServer…...
)
Matlab实现模拟退火算法(附上多个完整源码)
模拟退火算法(Simulated Annealing)是一种全局优化算法,其基本思想是通过模拟物理退火过程来寻找最优解。该算法可以应用于各种优化问题,如函数优化、组合优化、图形优化等。 文章目录 步骤简单案例完整仿真源码下载 步骤 在Mat…...
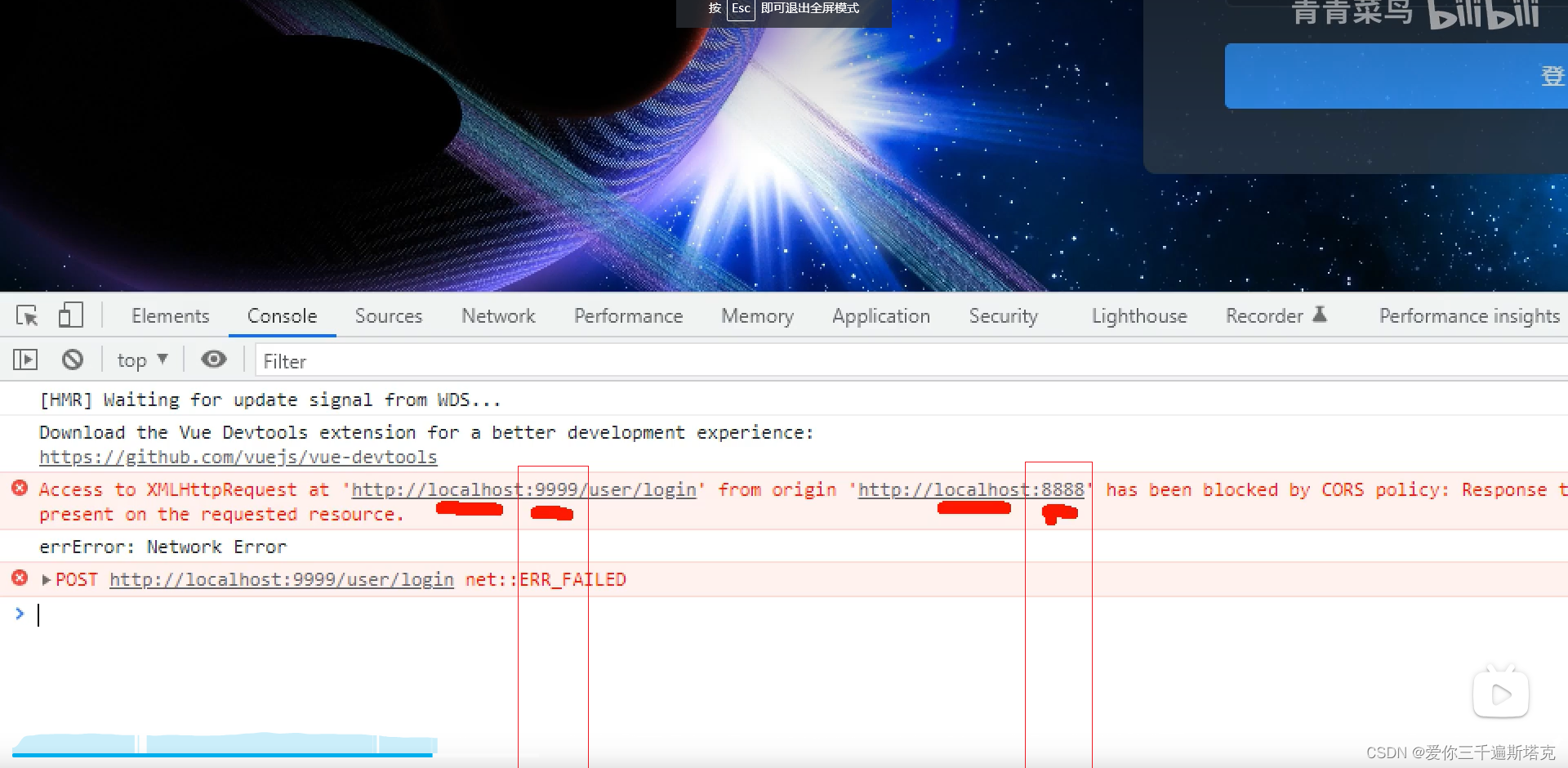
前后端分离------后端创建笔记(03)前后端对接(上)
本文章转载于【SpringBootVue】全网最简单但实用的前后端分离项目实战笔记 - 前端_大菜007的博客-CSDN博客 仅用于学习和讨论,如有侵权请联系 源码:https://gitee.com/green_vegetables/x-admin-project.git 素材:https://pan.baidu.com/s/…...

stable diffusion安装包和超火使用文档及提示词,数字人网址
一:文生图、图生图 1:stable diffusion:对喜欢二次元、美女小姐姐、大眼萌妹的人及其友好哈哈(o^^o) 1):关于安装包和模型包: 链接:https://pan.baidu.com/s/11_kguofh76gwhTBPUipepw 提取码…...

训练营:贪心篇
贪心就是:局部最优 1、455. 分发饼干 按照饼干分,从大到小,最大的给胃口最大能满足的 def findContentChildren455(g, s):g sorted(g,reverseTrue)s sorted(s,reverseTrue)j0c 0i0while(i<len(s) and j<len(g)):if s[i]>g[j]:c…...
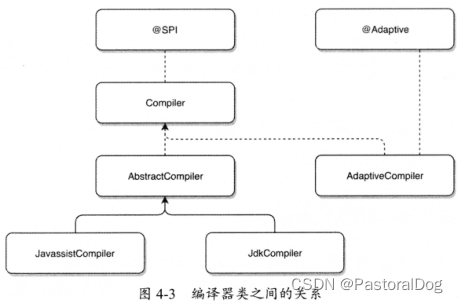
四、Dubbo扩展点加载机制
四、Dubbo扩展点加载机制 4.1 加载机制概述 Dubbo良好的扩展性与框架中针对不同场景使用合适设计模式、加载机制密不可分 Dubbo几乎所有功能组件都是基于扩展机制(SPI)实现的 Dubbo SPI 没有直接使用 Java SPI,在它思想上进行改进ÿ…...
[保研/考研机试] KY103 2的幂次方 上海交通大学复试上机题 C++实现
题目链接: KY103 2的幂次方 https://www.nowcoder.com/share/jump/437195121691999575955 描述 Every positive number can be presented by the exponential form.For example, 137 2^7 2^3 2^0。 Lets present a^b by the form a(b).Then 137 is present…...

时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价)
时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价) 目录 时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价)预测结果基本介绍程序设计参考资料 预测结果 基本介绍 Matlab实现BP神经网络时间序列预测未来(完整…...

组合模式(C++)
定义 将对象组合成树形结构以表示部分-整体’的层次结构。Composite使得用户对单个对象和组合对象的使用具有一致性(稳定)。 应用场景 在软件在某些情况下,客户代码过多地依赖于对象容器复杂的内部实现结构,对象容器内部实现结构(而非抽象接口)的变化…...

git上传问题记录
unable to access ‘https://github.com/songjiahao-wq/untitled.git/’: Failed to connect to github.com port 443 after 21086 ms: Couldn’t connect to serve 解决办法:修改 Git 的网络设置 打开git Bash运行,clash代理一般是下面的端口 # 注意…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

