C进阶(1/7)——数据在内存中的存储
目录
前言:
一.数据类型介绍
类型基本归类:
整型家族:
浮点数家族:
构造类型:
指针类型:
空类型:
二.整型在内存中的存储
1.原码,反码,补码
2.大小端介绍
3.练习巩固
三.浮点型数据的存储
1.浮点数存储与整型存储的关系
2.浮点数存储规则
3.IEEE 754对有效数字M和指数E,还有一些特别规定。
4.指数E
前言:
介绍整型和浮点型数据类型在内存中的存储,希望对你有所帮助。
一.数据类型介绍
整数类数据类型:只表示整数
浮点型:可表示具有小数部分的数值

以上类型又被叫做算术类型。
注意:C语言中没有字符串类型
那么为什么在编程语言中要区分数据类型呢?
1.使用这个类型开辟内存空间的大小(大小决定了使用范围)。
2.如何看待内存空间的视角
类型基本归类:
整型家族:
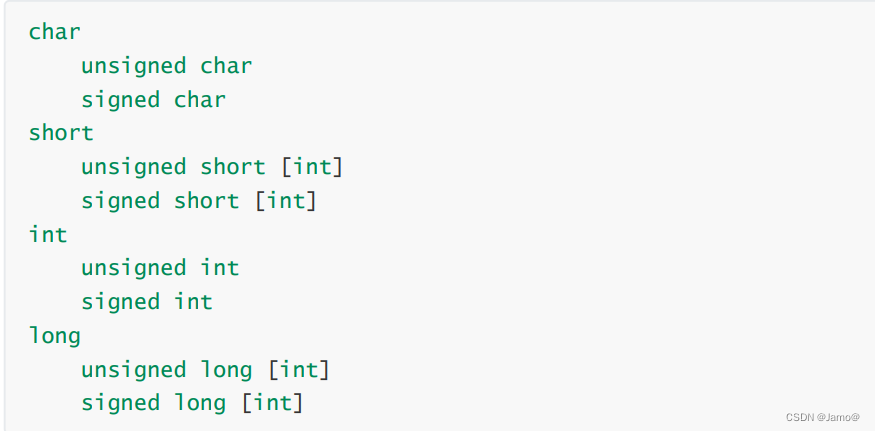
浮点数家族:

构造类型:
 指针类型:
指针类型:

空类型:

二.整型在内存中的存储
一个变量的创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。
我们来看看数据在所开辟内存中到底是如何存储的?

我们知道int整型在32位环境下占用四个字节大小,那该如何存储呢?
我们首先来了解如下概念:
1.原码,反码,补码
- 计算机中的整数有三种2进制表示方法,即原码、反码和补码。
- 三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位正数的原、反、补码都相同。
- 负整数的三种表示方法各不相同。

对于整形来说:数据存放内存中其实存放的是补码。
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统 一处理; 同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程 是相同的,不需要额外的硬件电路。
让我们来看看内存中如何存放的数据。
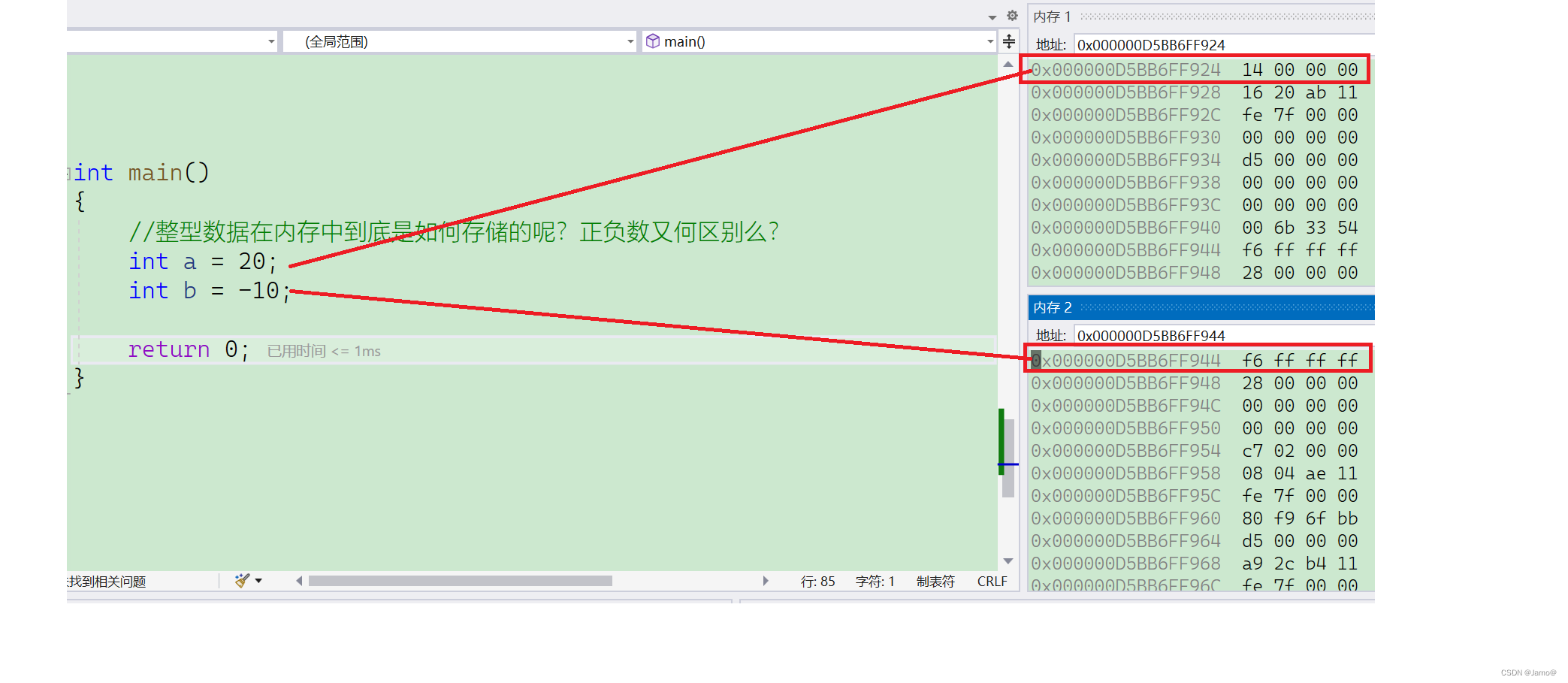
我们可以看到对于a和b分别存储的是补码。但是我们发现顺序有点不对劲。
这又是什么原因呢?
2.大小端介绍
什么是大端小端:
- 大端(存储)模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址 中;
- 小端(存储)模式,是指数据的低位保存在内存的低地址中,而数据的高位,,保存在内存的高地 址中。
大端存储相当于正着放置数据:

小端存储是逆着放置数据:

注意:我们是通过十六进制来表示的数据在内存中查看的也是十六进制表示的数据
我们下面通过一个代码来检测我当前使用的VS2022环境下是大端还是小端存储
#include <stdio.h>
int check_sys()
{int i = 1;return (*(char *)&i);
}
int main()
{int ret = check_sys();if(ret == 1){printf("小端\n");}else{printf("大端\n");}return 0;
}
运行发现:
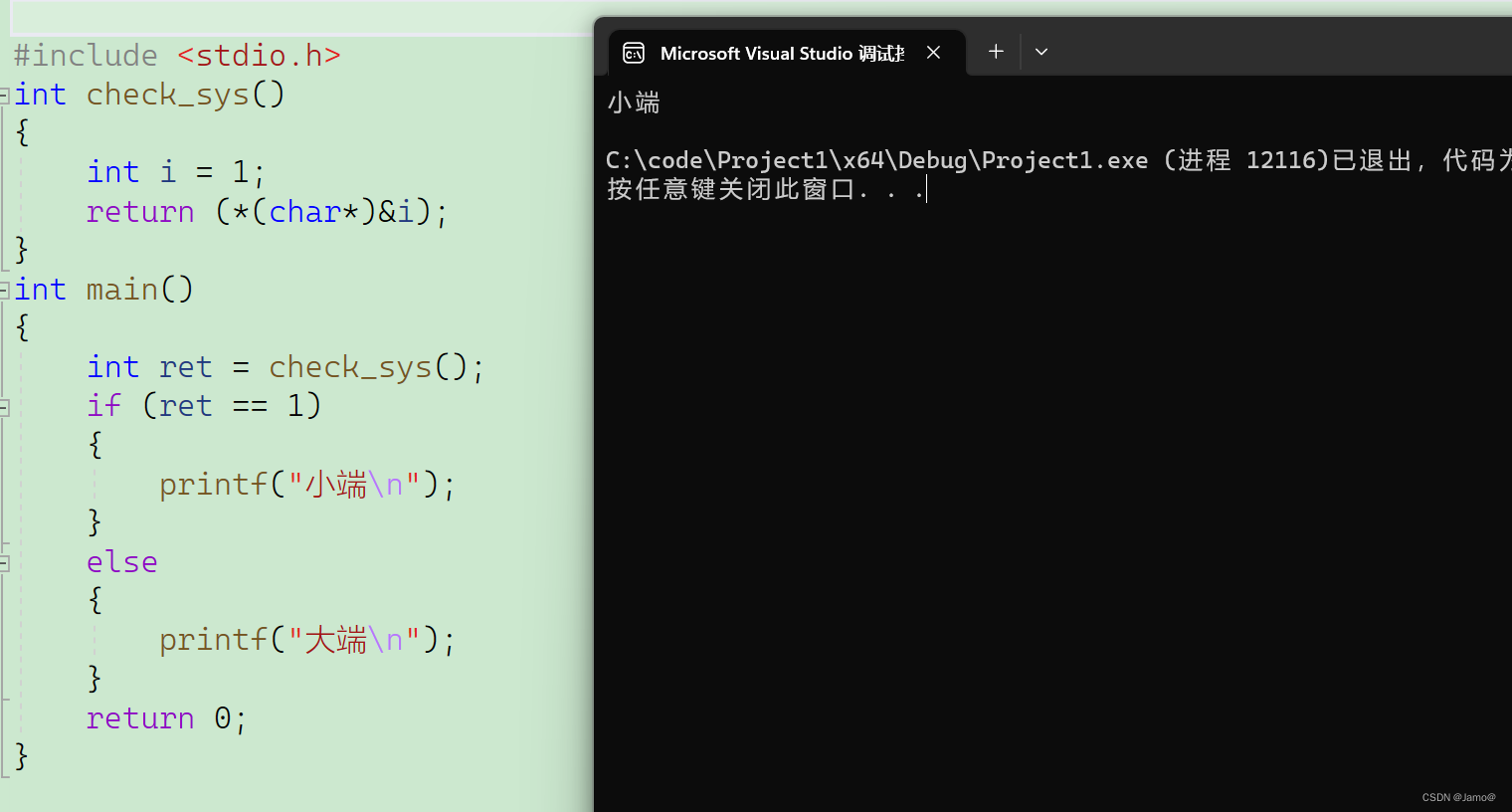
由此可见我们的VS2022使用的是小端存储。
数据存储的一种循环理解:我们以char类型来解释:


3.练习巩固
#include <stdio.h>
int main()
{char a= -1;signed char b=-1;unsigned char c=-1;printf("a=%d,b=%d,c=%d",a,b,c);return 0;
}
运行可得:

如下分析:
a=-1的原码反码补码如下

a的补码在存储时char类型会发生截断变为

当还原为原码时步骤如下符号位置不变其他位按位取反得到反码后再加一:

可知1000001二进制表示的就是-1
b为有符号整型可同理得出打印数据和存储数据一致
b=-1的原码反码补码如下
那为什么c却是255呢?
原因如下:

这就是数据在内存中存储方式因为数据类型不同而导致的。因此区分和正确使用数据类型十分的重要
下面的一些练习可以帮助你加深对数据存储的理解
#include <stdio.h>
int main()
{char a = -128;printf("%u\n",a);return 0;
}/*输出一个特别大的数字,首先a是有符号char类型的变量,存储-128的值,而%u是打印无符号整数的意思,所以这里的char类型会发生整型提升,从一个字节提升至4个字节,又因为a是负数,它的的符号位为1,所以整型提升时前面全部都是补的1,所以我们就得到了一个数的补码,而无符号数的源反补码都相同,所以我们就会得到一个特别大的数的源码.*/#include <stdio.h>
int main()
{char a = 128;printf("%u\n",a);return 0;
}
#include<stdio.h>
int main()
{char a[1000];int i;for(i=0; i<1000; i++){a[i] = -1-i;}printf("%d",strlen(a));return 0;
}#include <stdio.h>
unsigned char i = 0;
int main()
{for(i = 0;i<=255;i++){printf("hello world\n");}return 0;
}
三.浮点型数据的存储
1.浮点数存储与整型存储的关系
int main()
{int n = 9;float *pFloat = (float *)&n;printf("n的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);*pFloat = 9.0;printf("num的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);return 0;
}
num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
这就是因为浮点数和整型数据在内存中存储的方式不同而造成的。
2.浮点数存储规则
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法。
详细解读: 根据国际标准IEEE(电气和电子工程协会) 754
任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^S * M * 2^E
- (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- 2^E表示指数位。
举例来说: 十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。
那么,S=1,M=1.01,E=2。

相当于所有的浮点数都可以用S,M,E这三个数表示出来,所以我们的内存中只需要存储这三个数即可代表浮点数。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
3.有效数字M的特别规定。
前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。 IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的 xxxxxx部分。比如保存1.01的时 候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位 浮点数为例,留给M只有23位, 将第一位的1舍去以后,等于可以保存24位有效数字。
4.指数E的特别规定
1. E不全为0或不全为1:
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1。 比如: 0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其阶码为-1+127=126,表示为 01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进 制表示形式为:0 01111110 00000000000000000000000
2. E全为0:
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于 0的很小的数字。
3. E全为1:
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)。
本章内容较多需要多花功夫加深理解。感谢支持。
相关文章:

C进阶(1/7)——数据在内存中的存储
目录 前言: 一.数据类型介绍 类型基本归类: 整型家族: 浮点数家族: 构造类型: 指针类型: 空类型: 二.整型在内存中的存储 1.原码,反码,补码 2.大小端介绍 3.练…...
如何初始化Git仓库
如何将目录初始化为Git仓库 一级目录二级目录三级目录 一、准备1、安装 gh2、登录 二、初始化 Git 仓库 一级目录 二级目录 三级目录 一、准备 在这里,我们需要借助一个非常好用的工具,大家也可以参照官方文档进行阅读,下面介绍常用的…...
)
面试攻略,Java 基础面试 100 问(十三)
什么时候用 assert? assertion(断言)在软件开发中是一种常用的调试方式,很多开发语言中都支持这种机制。一般来说,assertion 用于保证程序最基本、关键的正确性。assertion 检查通常在开发和测试时开启。为了提高性能,在软件发布…...
将el-table中的展开列(expand)修改成slots自定义插槽
用过element-ui的有知道,展开这个箭头无法自定义,一点办法都没有,官方根本就没提供预留任何位置给你操作。 从下面图中,可以看到有两个插槽,默认插槽和表头插槽。 我们来扩展一个自定义插槽来实现我们想要的功能。…...

接入网概述
接入网概述 接入网基本概念接入网“最后一公里”解决方案数字用户线xDSL技术的发展与特点xDSL的局限性PON网络架构小结 接入网基本概念 在家里终端设备连接ONT然后进入接入网,这个接入网大概在2-20km左右,中间是通过光纤进行连接,是无源的&a…...

嵌入式要卷成下一个Java了吗?
不会! 说不会也是有自己的原因的 前几天写了一篇 Linux 和单片机的文章 不做Linux就没前途吗? 单片机容易,门槛低,无非不就是单片机技术知识点比较少,特别是面向过程式的编程也更容易掌握。嵌入式 Linux 是多任务式的&…...

项目中怎么做sql优化?
背景: 系统用着用着突然出现卡,数据加载慢。这个时候有可能是sql查询问题导致的。这个时候我们要怎么排查这个问题呢。如果排查后是sql问题的话我们应该怎么优化呢! 处理方案:第一步定位 可以开启MySQL的慢查询日志,设…...
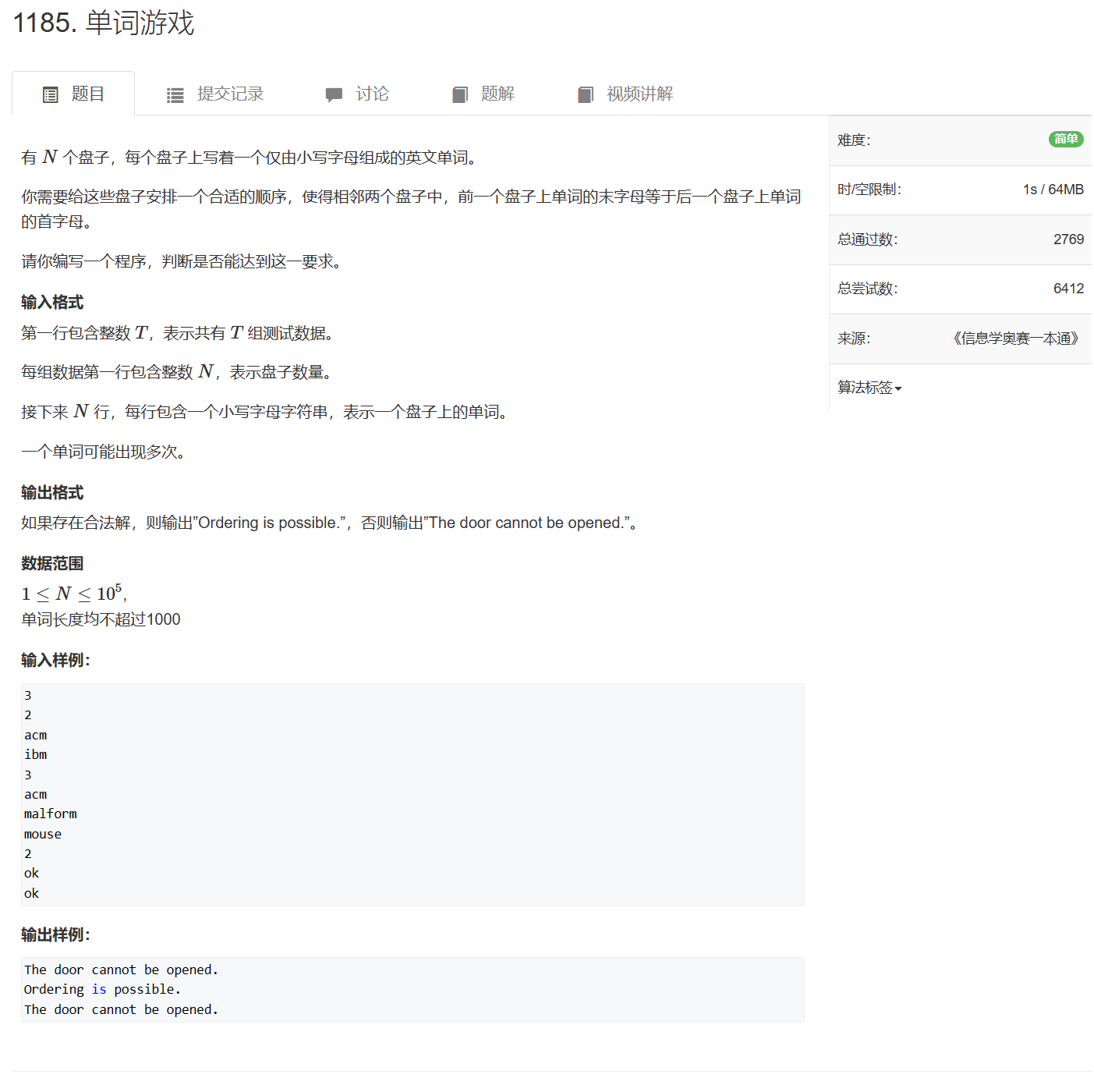
第三章 图论 No.12欧拉回路与欧拉路径
文章目录 定义欧拉路径的性质:1123. 铲雪车边编号输出欧拉路径:1184. 欧拉回路点编号字典序最小输出欧拉路径:1124. 骑马修栅栏并查集判断有向图是否存在欧拉路径:1185. 单词游戏 定义 小学一笔画问题,每条边只经过一次…...
)
kubernetes(二)
文章目录 1. kubernetes常用资源1.1 deployment资源1.2 deployment升级和回滚1.3 tomcat连接mysql1.4 wordpress 2. kubernetes的附加组件2.1 kubernetes集群配置dns服务2.2 kubernetes的dns配置文件2.3 namespace命名空间2.4 kubernetes健康检查2.4.1 健康检查livenessprobo2.…...

MATLAB算法实战应用案例精讲-【深度学习】预训练模型ELECTRAPerformer
目录 ELECTRA 1.介绍 2.模型结构 2.1 Replaced Token Detection 2.2 权重共享 2.3 更小的生成器 3...
微服务05-Sentinel流量防卫兵
随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以 流量 为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 S…...
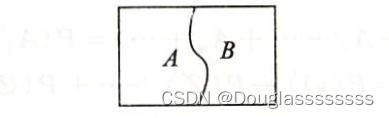
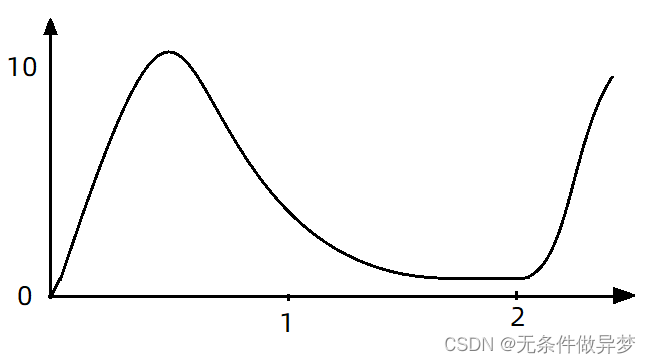
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件 1.1 随机试验 …...
【设计模式】建造者模式
建造者模式(Builder Pattern)使用多个简单的对象一步一步构建成一个复杂的对象。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 一个 Builder 类会一步一步构造最终的对象。该 Builder 类是独立于其他对象的。 介绍 …...

网络安全---正则回溯
目录 一、题目引入 二、举出回溯例子进行分析 第一步: 正则往前匹配 第二步:匹配到头 第三步:往回匹配 第四步:直到分号结束 (匹配上) 原因: 三、进入正题一(分析题型&#…...

压测秒杀场景常见问题
很多人在做秒杀场景的压测时,经常出现以下两个问题: 1,用自己的笔记本电脑瞬间发起1000个请求 2,没有使用虚拟ip(发起的请求都是同样的一个ip) 其实现在很多人在做秒杀压测的时候,都会遇到这两…...

【python】【sql】格式化注意事项
如果需要格式化表名到 sql 语句,sql 引擎是不支持的。 所以表名需要用字符串格式化,但其他参数最好用 sql 自带的格式,这样就不用去调一些细节,比如字符串的值是否要带引号之类的。 比如: cur.execute(SELECT {0} FR…...

leetcode做题笔记71
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请你将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外…...

啥是 Python?学了他能干嘛?
最近在学 python,真心感觉这玩意太牛了,你能想到,想不到的事情他都能做,前两天也是总结了一下 python 的特点,分享给大家看看~ 与君共勉 历史篇 1989年圣诞节,当大家都在忙着包装礼物,享受节日…...

百日筑基篇——Pandas学习三(pyhton入门八)
百日筑基篇——Pandas学习三(pyhton入门八) 文章目录 前言一、数据排序二、字符串处理三、数据合并方法1. merge方法2. concat方法 四、分组数据统计五、数据重塑1. stack2. pivot 总结 前言 上一篇文章介绍了一下pandas库中的一些函数,而本…...

【Android Framework系列】第10章 PMS之Hook实现广播的调用
1 前言 前面章节我们学习了【Android Framework系列】第4章 PMS原理我们了解了PMS原理,【Android Framework系列】第9章 AMS之Hook实现登录页跳转我们知道AMS可以Hook拦截下来实现未注册Activity页面的跳转,本章节我们来尝试一下HookPMS实现广播的发送。…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

