12-数据结构-数组、矩阵、广义表
数组、矩阵、广义表
目录
数组、矩阵、广义表
一、数组
二.矩阵
三、广义表
一、数组
这一章节理解基本概念即可。数组要看清其实下标是多少,并且二维数组,存取数据,要先看清楚是按照行存还是按列存,按行则是正常一行一行的去读写,按列则是,从左至右,一列一列的弄。
此外,数组中具体坐标的空间大小要会计算,每块存储单元,算到该数组坐标的前一位的数组大小:如A[5][3],起始位A[0][0],则计算A[5][3]的时候,先计算0-4行的空间大小,再计算第5行的大小,第五行的时候,是计算0-2列即0,1,2,三列,所以第五行空间个数为3,将其加上即可。
二、矩阵
则是掌握基本矩阵的代码,矩阵相加,相乘,转置。
- 其次要会压缩矩阵,压缩矩阵的目的是减少存储单元
- 方法是,给矩阵中的有效数据,存进一维数组中去。
- 这个时候就需要压缩矩阵的计算了,一般计算特殊矩阵:
- 对称阵,上三角下三角,画一个简单的矩阵,然后根据按行存或者按列存,进行存储,然后计算,一般是等差数列,然后加上最后一行或最后一列的有效数据,这个就看具体是多少了。一般遇到选择题,让求规律的,在看清矩阵和一维数组起始下标的前提下,找具体坐标试一下,如A[0][0]---0,在一维数组里面是第0个,给(行)i=0,(列)j=0,代入试一下即可。如果遇到算具体数值的,则是画一个大概矩阵,然后找规律。按行排列,则先计算0到i-1行的个数(一般为等差数列,第0行有1个,第1行有2个第i-1行有i个,则共0到i-1,总个数为i个,a1=1,an=i所以等差数列为(
),这是第0到i-1行的总个数,再计算第i行的个数,按列算,j+1个,所以总个数为
+j+1,但存进数组的话,若数组下标为1,则
+j+1+1,要看具体矩阵和数组的起始下标。
- 对三角矩阵,则是待定系数法,为了省事直接k=ai+bj+c,其中k为存进一维数组的下标,i为矩阵的行,j为矩阵的列,c为常数,然后再去带具体坐标去解方程组即可。但上面设的公式,还要看具体情况去设置,如果有的个数为等差数列,则肯定有行的平方或者列的平方。
- 之后是稀疏矩阵:矩阵中大部分都是0的矩阵。
稀疏矩阵的压缩,就是给矩阵中非零元素,存起来。
稀疏矩阵的顺序存储(设成结构体,里面包含各种变量)
1.三元组表示法
按行优先存储,所以稀疏矩阵三元组,不好逆置,逆置的话,需要按列重新搞一下。
三元组,就是数组结构体里定义三个变量,分别是行,列,以及坐标值。其中数组结构体,第一个里面存的是,矩阵信息,即共几行几列,有几个非零元素。因此如果题中有5个非零元素,则三元组数组,要5+1个数组空间。
稀疏矩阵转化三元组步骤:
1.先计算矩阵中非零元素个数。即二维数组遍历,非零的,count(计数器)+1。最后返回count。
2.之后定义一个三元组数组,然后开始写转换函数,返回类型为三元组指针类型,即返回三元组。先存储矩阵信息,再三元组数组第一个位置,随后定义个记录器,index=1,表示实际非零元素个数的下标,随后开始遍历,当矩阵元素不等于零的时候,存进index坐标下,随后行和列也记录,之后,index+1,后移动,直到遍历结束。
2.伪地址存储
数据结构体,里面变量为伪地址变量以及具体值。伪地址计算方法,可直接查,按照行或者列,从1开始,哪个位置非零,就记录。
稀疏矩阵的链式存储
1.邻接表法。
用一维数组(矩阵行)去索引,索引内容,坐标值,列下标,以及同行下一个非零元。
即同一行,串成一个链,只串同行非零元素。
2.十字链表
三、广义表
广义表时线性表的推广,不是线性表,而是层次结构,树。
每个广义表用()括住,广义表里面可以套广义表,每个广义表是一个小整体。广义表里面,可以由原子元素(单个值),可以是广义表。
广义表的深度,长度和表头表尾
深度:最多的层数,即广义表包含几个,查括号。化成树的话,为最底下的那个广义表。
长度:第一层元素个数,化成树的话,是第二层结点.
表头:广义表非空时,第一个元素。即表头为取第一个元素的值。
表尾:实际上是除了表头以外,其他构成的新的广义表。是个广义表。
例如:((a),(b,f),(v))
表头为:(a)//只包含a的广义表, 不是a,a是原子元素。
表尾:((b,f)(v)),新构成的广义表.
再对表尾求
表头:(b,f),广义表。 不是((b,f)),表头为取第一个元素
表尾:( (v) ),是个广义表,由广义表(v)构成,即删除表头,剩下组成的新的广义表,
广义表的链式存储
有两个结点,第一个为广义表结点,包含标记域,表头,表尾指针,第二个是原子元素结点,包含标记域,和具体值。其中标记域为1,表示广义表,标记域为0表示原子元素。
一般,先画出第一个广义表结点,然后头节点指向出来,尾指针指向尾结点,以此类推。
扩展的线性表存储结构
跟链式存储差不多,只不过后面的指针变成了,左孩子又兄弟了,头指针指向最左边的孩子,之后孩子的尾指针,指向同级的右兄弟。(这种一般先画成树的形式,好判断)
相关文章:
12-数据结构-数组、矩阵、广义表
数组、矩阵、广义表 目录 数组、矩阵、广义表 一、数组 二.矩阵 三、广义表 一、数组 这一章节理解基本概念即可。数组要看清其实下标是多少,并且二维数组,存取数据,要先看清楚是按照行存还是按列存,按行则是正常一行一行的去读…...
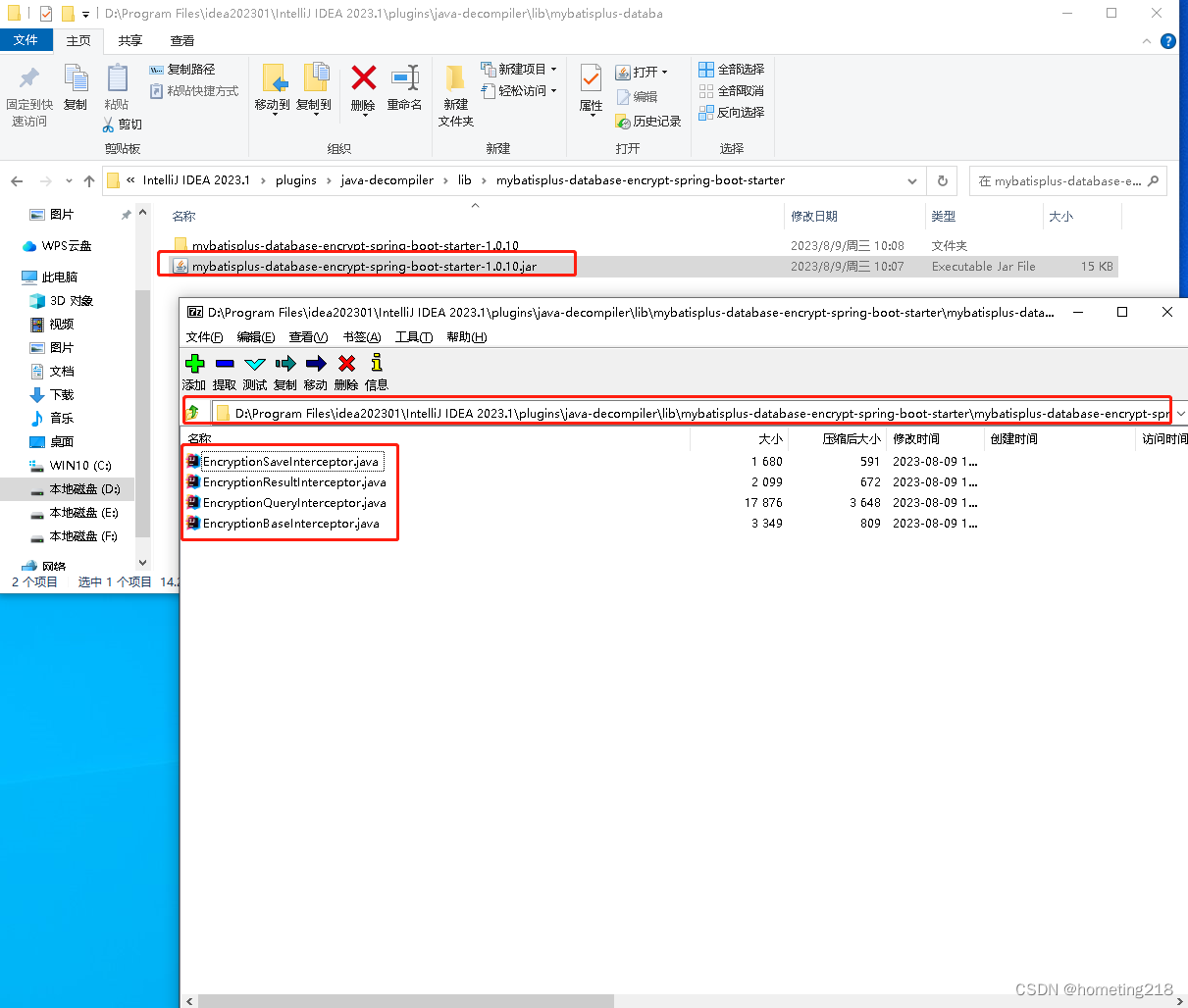
Idea 反编译jar包
实际项目中,有时候会需要更改jar包源码来达到业务需求,本文章将介绍一下如何通过Idea来进行jar反编译 1、Idea安装decompiler插件 2、找到decompiler插件文件夹 decompiler插件文件夹路径为:idea安装路径/plugins/java-decompiler/lib 3、…...
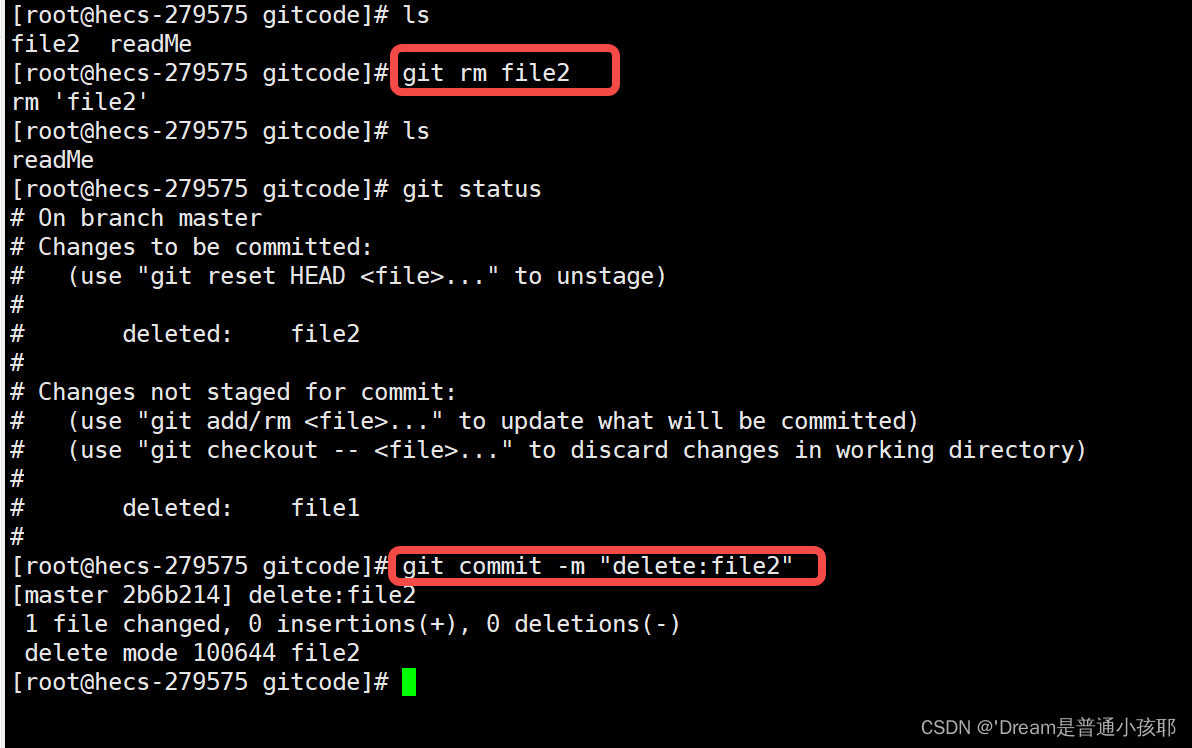
【Git】安装以及基本操作
目录 一、初识Git二、 在Linux底下安装Git一)centOS二)Ubuntu 三、 Git基本操作一) 创建本地仓库二)配置本地仓库三)认识工作区、暂存区、版本库四)添加文件五)查看.git文件六)修改文…...
)
Spring创建Bean的过程(2)
上一节介绍了Spring创建过程中的两个重要的接口,那么它们在创建Bean的过程中起到了什么作用呢?接下来请看: Spring有三种方式寻找 xml 配置文件,根据 xml 文件内容来构建 ApplicationContext,分别为ClassPathXmlAppli…...

Linux 终端操作命令(2)内部命令
Linux 终端操作命令 也称Shell命令,是用户与操作系统内核进行交互的命令解释器,它接收用户输入的命令并将其传递给操作系统进行执行,可分为内部命令和外部命令。内部命令是Shell程序的一部分,而外部命令是独立于Shell的可执行程序…...
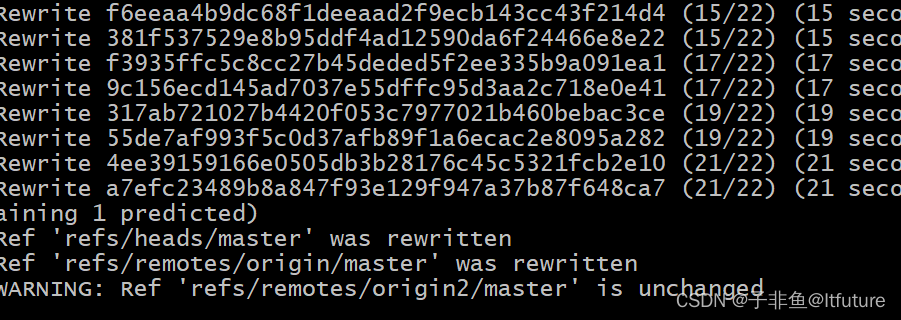
【Git】大大大问题之syntax error near unexpected token `(‘ 的错误解决办法
话不多说,先上图: 如图,因为在linux环境里,文件路径中含有括号(),因此报错! 解决办法 等同于 :linux下解决bash: syntax error near unexpected token (’ 的错误&am…...
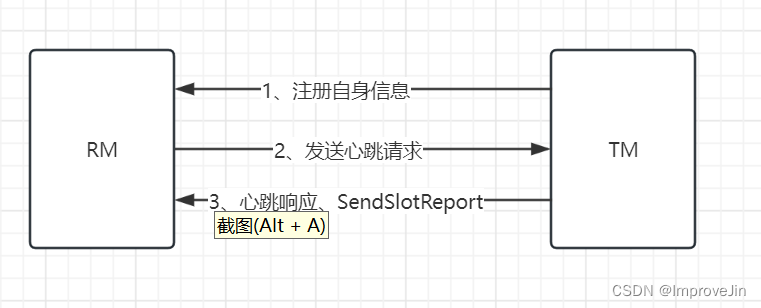
Flink源码之TaskManager启动流程
从启动命令flink-daemon.sh可以看出TaskManger入口类为org.apache.flink.runtime.taskexecutor.TaskManagerRunner TaskManagerRunner::main TaskManagerRunner::runTaskManagerProcessSecurely TaskManagerRunner::runTaskManager //构造TaskManagerRunner并调用start()方法 …...

加入微软MCPP有什么优势?
目录 专业认可 技术支持 销售和市场推广支持 培训和认证 业务机会和合作伙伴网络...

leetcode做题笔记78子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 思路一:回溯 void backtracking(int* nums, int numsSize, int** res, int* ret…...

Skywalking-9.6.0系列之本地源码编译并启动
Skywalking相信有很多人使用过,通过容器或者下载安装包进行安装的,今天从源代码角度,拉取、构建、启动。 官方文档步骤简洁明了,我这边会结合自己遇到的一些问题做出总结。 当前构建资源版本: MAC 10.15.7IDEA 2021.…...
proteus结合keil-arm编译器构建STM32单片机项目进行仿真
proteus是可以直接创建设计图和源码的,但是源码编译它需要借助keil-arm编译器,也就是我们安装keil-mdk之后自带的编译器。 下面给出一个完整的示例,主要是做一个LED灯闪烁的效果。 新建工程指定路径,Schematic,PCB layout都选择默…...

第五十三天
●剪辑——Pr 剪辑(Film editing),即将影片制作中所拍摄的大量素材,经过选择、取舍、分解与组接,最终完成一个连贯流畅、含义明确、主题鲜明并有艺术感染力的作品。 •线性编辑 将素材按时间顺序连接成新的连续画面的技术 •非线性编辑 …...

gorm基本操作
一、gorm安装 1.下载gorm go get -u gorm.io/gorm //gorm框架 go get -u gorm.io/driver/mysql //驱动2.mysql准备工作 mysql> create database godb; mysql> grant all on *.* to admin% identified by golang123!; mysql> flush privileges;3.导入gorm框架 impo…...
)
华为OD机试 - 排队游戏(Java JS Python)
题目描述 新来的老师给班里的同学排一个队。 每个学生有一个影力值。 一些学生是刺头,不会听老师的话,自己选位置,非刺头同学在剩下的位置按照能力值从小到大排。 对于非刺头同学,如果发现他前面有能力值比自己高的同学,他不满程度就增加,增加的数量等于前面能力值比…...

滚动条样式更改
::-webkit-scrollbar 滚动条整体部分,可以设置宽度啥的 ::-webkit-scrollbar-button 滚动条两端的按钮 ::-webkit-scrollbar-track 外层轨道 ::-webkit-scrollbar-track-piece 内层滚动槽 ::-webkit-scrollbar-thumb 滚动的滑块 ::-webkit-scrollbar…...
掌握Python的X篇_33_MATLAB的替代组合NumPy+SciPy+Matplotlib
numPy 通常与 SciPy( Scientific Python )和 Matplotlib (绘图库)一起使用,这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。 文章目录 1. numpy1.1 numpy简介1.2 矩阵类型的nparra…...

Python解决-力扣002-两数相加
两数相加:链表表示的逆序整数求和 在这篇技术博客中,我们将讨论一个力扣(LeetCode)上的编程题目:两数相加。这个问题要求我们处理两个非空链表,它们表示两个非负整数。每个链表中的数字都是逆序存储的&…...
nginx基于源码安装的方式对静态页面、虚拟主机(IP、端口、域名)和日志文件进行配置
一.静态页面 1.更改页面内容 2.更改配置文件 3.测试 二.虚拟主机配置 1.基于IP (1)在html目录下新建目录存放测试文件 (2)修改nginx.conf文件,在htttp模块中配置两个server模块分别对应两个IP (3&am…...
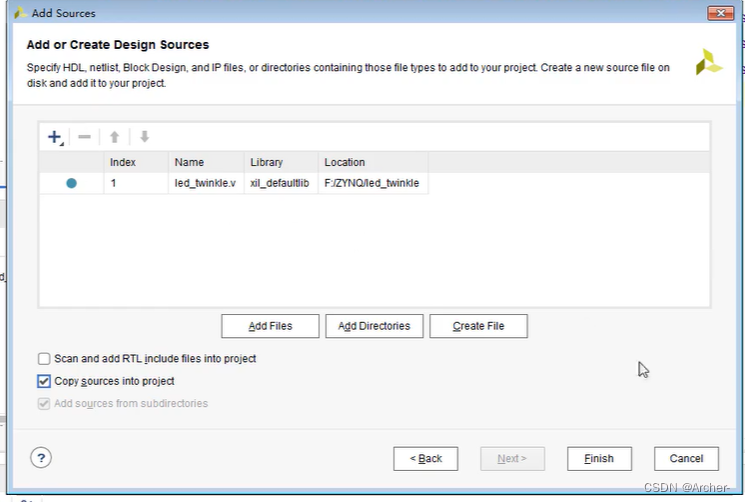
[FPAG开发]使用Vivado创建第一个程序
1 打开Vivado软件,新建项目 选择一个纯英文路径 选择合适的型号 产品型号ZYNQ-7010xc7z010clg400-1ZYNQ-7020xc7z010clg400-2 如果型号选错,可以单击这里重新选择 2 创建工程源文件 可以看到文件创建成功 双击文件打开,插入代码 modul…...
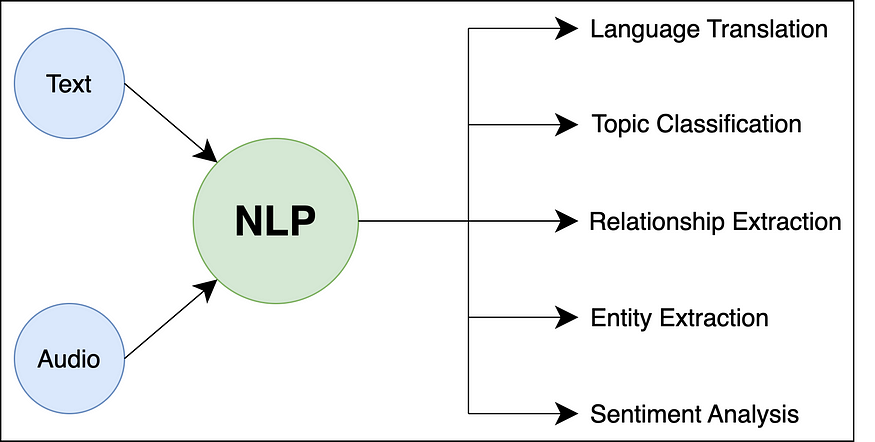
使用 Python 在 NLP 中进行文本预处理
一、说明 自然语言处理 (NLP) 是人工智能 (AI) 和计算语言学的一个子领域,专注于使计算机能够理解、解释和生成人类语言。它涉及计算机和自然语言之间的交互,允许机器以对人类有意义和有用的方式处理、分析…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
