掌握Python的X篇_33_MATLAB的替代组合NumPy+SciPy+Matplotlib
numPy 通常与 SciPy( Scientific Python )和 Matplotlib (绘图库)一起使用,这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
文章目录
- 1. numpy
- 1.1 numpy简介
- 1.2 矩阵类型的nparray
- 2. Matplotlib
- 2.1 Matplotlib简介
- 2.2 Matplotlib使用实例
1. numpy
1.1 numpy简介
numpy /nampai/数值计算库,简单而言,可以被当做向量,线性代数计算。
pip install numpy
官方推荐导入方式:
以np的别名导入numpy,这可能是因为历史遗留问题,有些第三方库是以np的别名导入的numpy库。
import numpy as np
使用实例:
In [11]: import numpy as npIn [12]: np.pi
Out[12]: 3.1415926535897931.2 矩阵类型的nparray
In [14]: x = np.linspace(-2*np.pi,2*np.pi,100) #在-2pi到2pi这个范围得到100个点,得到一个向量
In [15]: type(x)
Out[15]: numpy.ndarray
In [16]: x
Out[16]:
array([-6.28318531, -6.15625227, -6.02931923, -5.9023862 , -5.77545316,-5.64852012, -5.52158709, -5.39465405, -5.26772102, -5.14078798,-5.01385494, -4.88692191, -4.75998887, -4.63305583, -4.5061228 ,-4.37918976, -4.25225672, -4.12532369, -3.99839065, -3.87145761,-3.74452458, -3.61759154, -3.4906585 , -3.36372547, -3.23679243,-3.10985939, -2.98292636, -2.85599332, -2.72906028, -2.60212725,-2.47519421, -2.34826118, -2.22132814, -2.0943951 , -1.96746207,-1.84052903, -1.71359599, -1.58666296, -1.45972992, -1.33279688,-1.20586385, -1.07893081, -0.95199777, -0.82506474, -0.6981317 ,-0.57119866, -0.44426563, -0.31733259, -0.19039955, -0.06346652,0.06346652, 0.19039955, 0.31733259, 0.44426563, 0.57119866,0.6981317 , 0.82506474, 0.95199777, 1.07893081, 1.20586385,1.33279688, 1.45972992, 1.58666296, 1.71359599, 1.84052903,1.96746207, 2.0943951 , 2.22132814, 2.34826118, 2.47519421,2.60212725, 2.72906028, 2.85599332, 2.98292636, 3.10985939,3.23679243, 3.36372547, 3.4906585 , 3.61759154, 3.74452458,3.87145761, 3.99839065, 4.12532369, 4.25225672, 4.37918976,4.5061228 , 4.63305583, 4.75998887, 4.88692191, 5.01385494,5.14078798, 5.26772102, 5.39465405, 5.52158709, 5.64852012,5.77545316, 5.9023862 , 6.02931923, 6.15625227, 6.28318531])In [17]: y = np.cos(x) #每个点进行计算In [18]: y
Out[18]:
array([ 1. , 0.99195481, 0.9679487 , 0.92836793, 0.87384938,0.80527026, 0.72373404, 0.63055267, 0.52722547, 0.41541501,0.29692038, 0.17364818, 0.04758192, -0.07924996, -0.20480667,-0.32706796, -0.44406661, -0.55392006, -0.65486073, -0.74526445,-0.82367658, -0.88883545, -0.93969262, -0.97542979, -0.99547192,-0.99949654, -0.98743889, -0.95949297, -0.91610846, -0.85798341,-0.78605309, -0.70147489, -0.60560969, -0.5 , -0.38634513,-0.26647381, -0.14231484, -0.01586596, 0.1108382 , 0.23575894,0.35688622, 0.47227107, 0.58005691, 0.67850941, 0.76604444,0.84125353, 0.90292654, 0.95007112, 0.9819287 , 0.99798668,0.99798668, 0.9819287 , 0.95007112, 0.90292654, 0.84125353,0.76604444, 0.67850941, 0.58005691, 0.47227107, 0.35688622,0.23575894, 0.1108382 , -0.01586596, -0.14231484, -0.26647381,-0.38634513, -0.5 , -0.60560969, -0.70147489, -0.78605309,-0.85798341, -0.91610846, -0.95949297, -0.98743889, -0.99949654,-0.99547192, -0.97542979, -0.93969262, -0.88883545, -0.82367658,-0.74526445, -0.65486073, -0.55392006, -0.44406661, -0.32706796,-0.20480667, -0.07924996, 0.04758192, 0.17364818, 0.29692038,0.41541501, 0.52722547, 0.63055267, 0.72373404, 0.80527026,0.87384938, 0.92836793, 0.9679487 , 0.99195481, 1. ])numPy 通常与 SciPy( Scientific Python )和 Matplotlib (绘图库)一起使用,这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
2. Matplotlib
2.1 Matplotlib简介
安装:
In [19]: pip install matplotlib
如果安装失败,可以尝试升级pip,命令如下:
python -m pip install -U pip
官网 : https://matplotlib.org/
官方推荐导入方式:
import matplotlib.pyplot as plt
2.2 Matplotlib使用实例
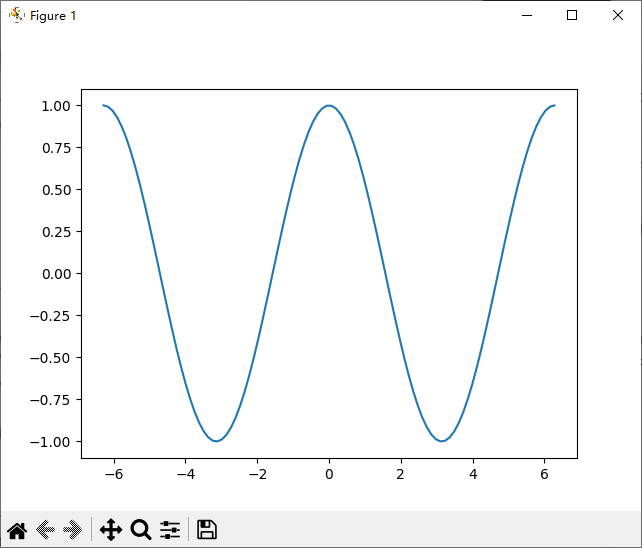
实例1:绘制cos图
In [21]: plt.plot(x,y)
In [21]: plt.plot(x,y)
Installed tk event loop hook.
Out[21]: [<matplotlib.lines.Line2D at 0x2b20f74b760>]
In [23]: plt.show()
运行结果:
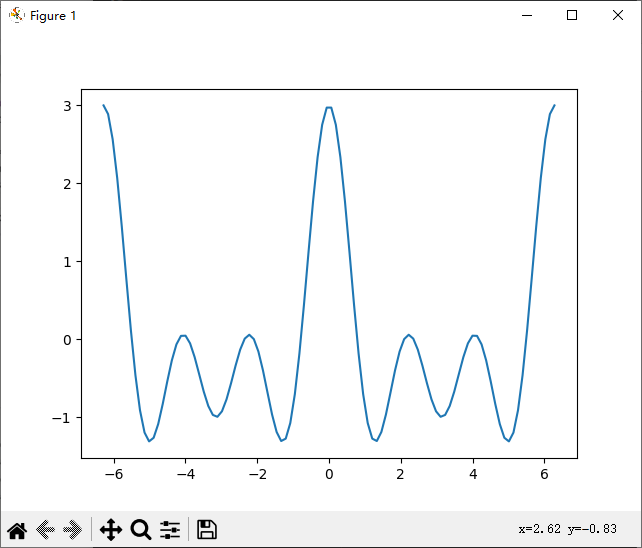
实例2:以脚本形式,绘制复杂的图
import numpy as np
import matplotlib.pyplot as pltif __name__ == "__main__":x = np.linspace(-2*np.pi,2*np.pi,100)y = np.cos(x) + np.cos(2*x) + np.cos(3*x)plt.plot(x,y)plt.show()
运行结果如下:
3. 学习视频地址:MATLAB的替代组合NumPy+SciPy+Matplotlib
相关文章:

掌握Python的X篇_33_MATLAB的替代组合NumPy+SciPy+Matplotlib
numPy 通常与 SciPy( Scientific Python )和 Matplotlib (绘图库)一起使用,这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。 文章目录 1. numpy1.1 numpy简介1.2 矩阵类型的nparra…...

Python解决-力扣002-两数相加
两数相加:链表表示的逆序整数求和 在这篇技术博客中,我们将讨论一个力扣(LeetCode)上的编程题目:两数相加。这个问题要求我们处理两个非空链表,它们表示两个非负整数。每个链表中的数字都是逆序存储的&…...
nginx基于源码安装的方式对静态页面、虚拟主机(IP、端口、域名)和日志文件进行配置
一.静态页面 1.更改页面内容 2.更改配置文件 3.测试 二.虚拟主机配置 1.基于IP (1)在html目录下新建目录存放测试文件 (2)修改nginx.conf文件,在htttp模块中配置两个server模块分别对应两个IP (3&am…...
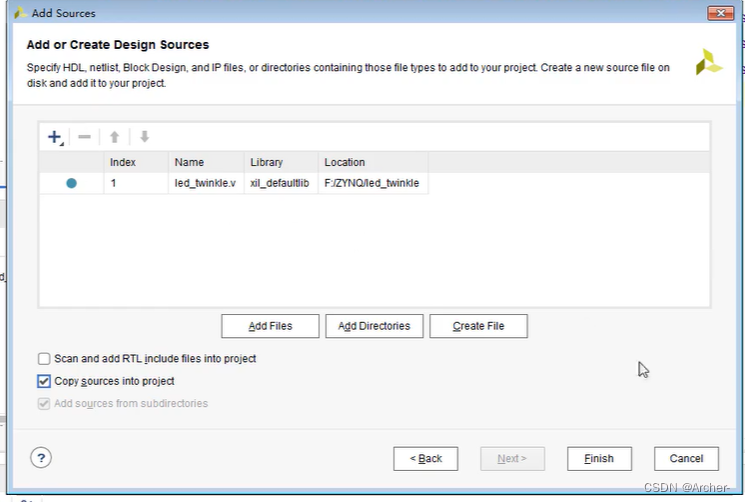
[FPAG开发]使用Vivado创建第一个程序
1 打开Vivado软件,新建项目 选择一个纯英文路径 选择合适的型号 产品型号ZYNQ-7010xc7z010clg400-1ZYNQ-7020xc7z010clg400-2 如果型号选错,可以单击这里重新选择 2 创建工程源文件 可以看到文件创建成功 双击文件打开,插入代码 modul…...
使用 Python 在 NLP 中进行文本预处理
一、说明 自然语言处理 (NLP) 是人工智能 (AI) 和计算语言学的一个子领域,专注于使计算机能够理解、解释和生成人类语言。它涉及计算机和自然语言之间的交互,允许机器以对人类有意义和有用的方式处理、分析…...
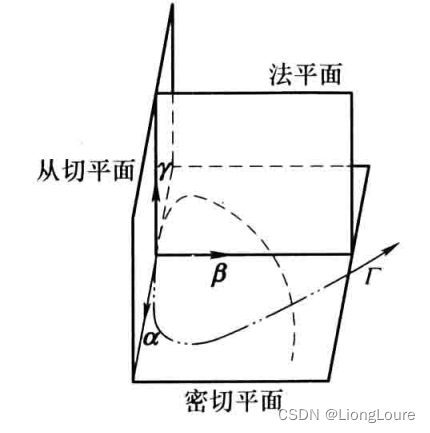
[足式机器人]Part3机构运动微分几何学分析与综合Ch03-1 空间约束曲线与约束曲面微分几何学——【读书笔记】
本文仅供学习使用 本文参考: 《机构运动微分几何学分析与综合》-王德伦、汪伟 《微分几何》吴大任 Ch01-4 平面运动微分几何学 3.1 空间曲线微分几何学概述3.1.1 矢量表示3.1.2 Frenet标架 连杆机构中的连杆与连架杆构成运动副,该运动副元素的特征点或特…...

pytest框架快速进阶篇-pytest前置和pytest后置,skipif跳过用例
一、Pytest的前置和后置方法 1.Pytest可以集成unittest实现前置和后置 importunittestimportpytestclassTestCase(unittest.TestCase):defsetUp(self)->None:print(unittest每个用例前置)deftearDown(self)->None:print(unittest每个用例后置)classmethoddefsetUpClass…...

Python 基础语法 | 常量表达式,变量,注释,输入输出
常量和表达式 我们可以把 Python 当成一个计算器,来进行一些算术运算 print(1 2 - 3) # 0 print(1 2 * 3) # 7 print(1 2 / 3) # 1.6666666666666665注意: print 是一个 Python 内置的 函数可以使用 - * / () 等运算符进行算术运算,先…...

SQL | 分组数据
10-分组数据 两个新的select子句:group by子句和having子句。 10.1-数据分组 上面我们学到了,使用SQL中的聚集函数可以汇总数据,这样,我们就能够对行进行计数,计算和,计算平均数。 目前为止,…...
)
软件测试技术之如何编写测试用例(6)
四、客户端兼容性测试 1、平台测试 市场上有很多不同的操作系统类型,最常见的有Windows、Unix、Macintosh、Linux等。Web应用系统的最终用户究竟使用哪一种操作系统,取决于用户系统的配置。这样,就可能会发生兼容性问题,同一个应…...

论文阅读——Adversarial Eigen Attack on Black-Box Models
Adversarial Eigen Attack on Black-Box Models 作者:Linjun Zhou, Linjun Zhou 攻击类别:黑盒(基于梯度信息),白盒模型的预训练模型可获得,但训练数据和微调预训练模型的数据不可得ÿ…...
-[自定义对话记忆与自定义记忆类])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[自定义对话记忆与自定义记忆类]
分类目录:《自然语言处理从入门到应用》总目录 自定义对话记忆 本节介绍了几种自定义对话记忆的方法: from langchain.llms import OpenAI from langchain.chains import ConversationChain from langchain.memory import ConversationBufferMemoryllm…...

【C/C++】STL queue 非线程安全接口,危险!
STL 中的 queue 是非线程安全的,一个组合操作:front(); pop() 先读取队首元素然后删除队首元素,若是有多个线程执行这个组合操作的话,可能会发生执行序列交替执行,导致一些意想不到的行为。因此需要重新设计线程安全的…...
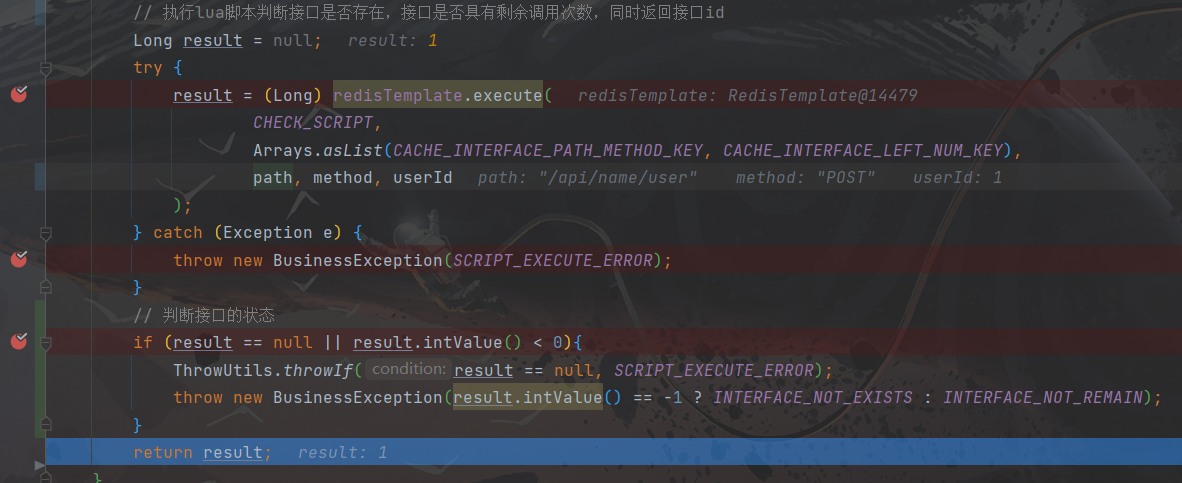
执行Lua脚本后一直查询不到Redis中的数据(附带问题详细排查过程,一波三折)
文章目录 执行Lua脚本后一直查询不到Redis中的数据(附带详细问题排查过程,一波三折)问题背景问题1:Lua脚本无法切库问题2:RedisTemlate切库报错问题3:序列化导致数据不一致问题4:Lua脚本中单引号…...
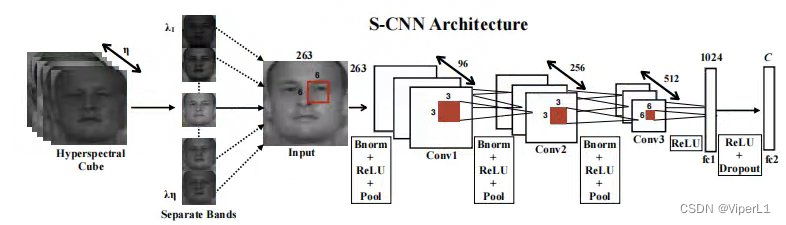
[高光谱]PyTorch使用CNN对高光谱图像进行分类
项目原地址: Hyperspectral-Classificationhttps://github.com/eecn/Hyperspectral-ClassificationDataLoader讲解: [高光谱]使用PyTorch的dataloader加载高光谱数据https://blog.csdn.net/weixin_37878740/article/details/130929358 一、模型加载 在…...
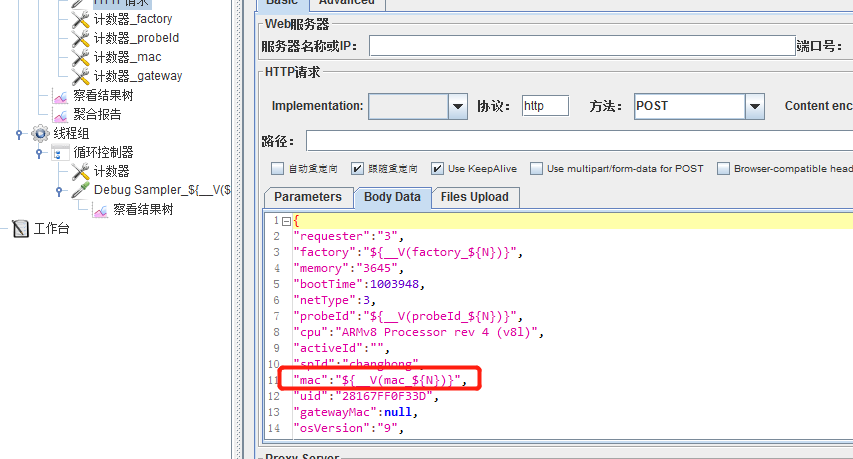
jmeter获取mysql数据
JDBC Connection Configuration Database URL: jdbc:mysql:// 数据库地址 /库名 JDBC Driver class:com.mysql.jdbc.Driver Username:账号 Password:密码 JDBC Request 字段含义 字段含义 Variable Name Bound to Pool 数据库连接池配置…...
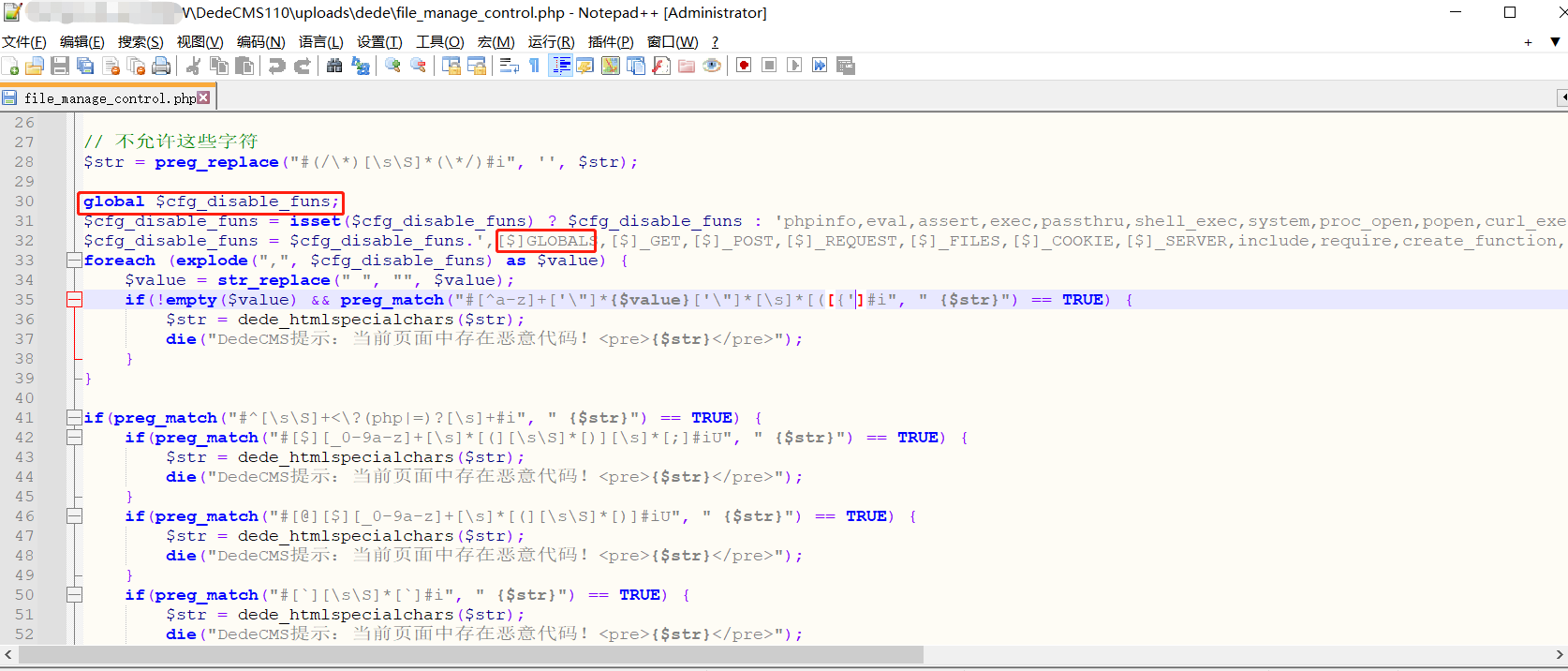
Dedecms V110最新版RCE---Tricks
前言 刚发现Dedecms更新了发布版本,顺便测试一下之前的day有没有修复,突然想到了新的tricks去实现RCE。 文章发布的时候估计比较晚了,一直没时间写了。 利用 /uploads/dede/article_string_mix.php /uploads/dede/article_template_rand.…...
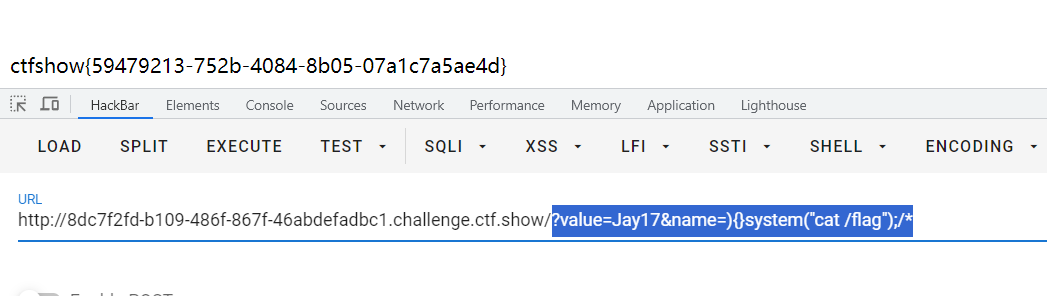
CTFshow 限时活动 红包挑战7、红包挑战8
CTFshow红包挑战7 写不出来一点,还是等了官方wp之后才复现。 直接给了源码 <?php highlight_file(__FILE__); error_reporting(2);extract($_GET); ini_set($name,$value);system("ls ".filter($_GET[1])."" );function filter($cmd){$cmd…...

Redis使用Lua脚本和Redisson来保证库存扣减中的原子性和一致性
文章目录 前言1.使用SpringBoot Redis 原生实现方式2.使用redisson方式实现3. 使用RedisLua脚本实现3.1 lua脚本代码逻辑 3.2 与SpringBoot集成 4. Lua脚本方式和Redisson的方式对比5. 源码地址6. Redis从入门到精通系列文章7. 参考文档 前言 背景:最近有社群技术交…...
【从零开始学Kaggle竞赛】泰坦尼克之灾
目录 0.准备1.问题分析挑战流程数据集介绍结果提交 2.代码实现2.1 加载数据2.1.1 加载训练数据2.1.2 加载测试数据 2.2 数据分析2.3 模型建立与预测 3.结果提交 0.准备 注册kaggle账号后,进入titanic竞赛界面 https://www.kaggle.com/competitions/titanic 进入后界…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
