当前位置： 首页 > news >正文

资料分析（三）—— 基期、现期、人口、增长量

news 2026/5/26 13:50:42

基期

基期值 = 现期值 - 增长量 = 增长量/增长率 = 现期值/1+（间隔)增长率

化除为乘 ：当增长率｜r| <= 5% 时，\frac{A}{1+r} = A - A*R，\frac{A}{1-r} \approx A + A*r

注：当选项首位相同，第二位也相同时，只能用直除

基期和差 =  \frac{A}{1+a} - \frac{B}{1+b} (结合选项，厂除）

现期

现期值 = 基期值 + 增长量

保持增长量：基期值 + 增长量 ✖️ n (增长趋势）

保持增长率：基期值 ✖️（1+增长率）

不给增长率：r > 0, 增长量上升（反向利用选项）

按名义增长率求现期：现期值/ 1+ 名义增长率（1 + 实际增长率）    （给现期求现期）

人口

人口自然增长率 = 出生人口 - 死亡人口 / 年平均人口数

出生率 = 年内出生人数 / 年内总人数

增长量

公式

给现期和基期：

现期值 - 基期值

给现期和增长率：

现期值 / 1+ 增长率 ✖️ 增长率

百化分 ｜r｜ = 1/n 

  • 增长量 = 现期值 ➗ （n+1） r > 0
  • 减少量 = 现期值 ➗ （n-1） r < 0

放缩

3.33% = 33.3% ➗ 10 = 1/3 ➗ 10 = 1/30

取中

22.2% = 1/4.5  18.2% = 1/5.5  15.4% = 1/6.5

13.3% = 1/7.5  11.8% = 1/8.5  10.5% = 1/9.5

10.5% = 1/9.5

| r | < 5%

增长量 \approx 现期值 ✖️ 增长率

r > 100%

百化分或截位计算

倍数

多步除法，根据选项，截位列式

拉动增长率

拉动增长率 = 部分增长量 / 整体基期值

注：一般情况下，年份差n = 现期年份 - 基期年份 
五年规划期间（或考官限定）：年份差为5年，基期往前推一年

五年规划：（基期往前推一年）

  • “十五期间” — — 2001年 - 2005年
  • “十一五期间” — — 2006年 - 2010年
  • “十二五期间” — — 2011年 - 2015年
  • “十一五期间” — — 2016年 - 2020年

年均增长量

年均增长量 = 末期值 - 初期值 / 年份差n

识别：平均每年增加... + 单位

比较大小

识别：增加/减少 + 最多/最少

给现期和基期

柱形图、折线图可看高度差

给现期和增长量

  • 同大则小，大大则大
  • 一大一小，分数比较，百化分

增长量绝对值比较

淘汰赛

增长率（r）

易错点

百分数与百分点

增长率与倍数：倍数 = 增长率 + 1

成数与翻番：30% = 3成；翻一番 = 2倍

增幅、降幅与变化幅度 降幅和变化幅度带绝对值进行比较

增幅 带符号进行比较 “高减低加” 正的不存在“降幅”

可正可负

降幅

必须为负，如“-20%”，降幅20%

变化（量）幅度

带r的绝对值比较，只看数值

解法

百分点

增幅：带正负号 高减低加

降幅： 带绝对值 高减低加

公式

给现期和基期

（现期值 - 基期值 ）/ 基期值 = 现期值 / 基期值 - 1

给现期和增长量

增长量 /（现期值 - 增长量）= 增长量 / 基期值

比较大小

识别：增加、减少 + 最快/最慢

给现期和基期

  • 当 现期值 / 基期值 >= 2时，现期值/基期值 比较，当现期值/基期值 \approx 1时，用 增长量/基期值 比较（技巧：增长量变大，基期值变大，增长率变小
  • 增长率者折线图、增长率排序

给现期和增长量

增长量 / 基期量 比较，计算只能用增长量/基期量

特定增长率

  • 超过10%：现期值 > 1.1 × 基期值 （错位相加）
  • 超过20%：现期值 > 1.2 × 基期值 （错位2位）
  • 超过50%：现期值 > 1.5 × 基期值 （加本身一半）
  • 超过100%：2 × 增长量 > 现期值

间隔增长率

常用公式

r1 + r2 + r3 (r1, r2 绝对值小于10%时，r1r2可忽略）

间隔倍数

间隔增长率 + 1

间隔基期

现期值 / 1 + (间隔）增长率

相关文章：

资料分析（三）—— 基期、现期、人口、增长量

基期 基期值 现期值 - 增长量 增长量/增长率 现期值/1&#xff08;间隔)增长率 化除为乘 &#xff1a;当增长率&#xff5c;r| < 5% 时&#xff0c;&#xff0c; 注&#xff1a;当选项首位相同&#xff0c;第二位也相同时&#xff0c;只能用直除 基期和差 (结合选…...

编程日记 2023/8/15 7:56:21

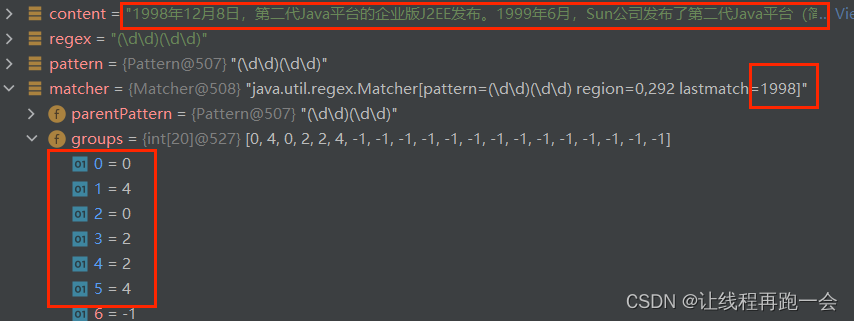
Java 正则表达式【匹配与分组基本原理】

简介 我们一般使用正则表达式是用来处理字符串的&#xff0c;不管是实际的开发中还是我们的算法竞赛中&#xff0c;使用正则表达式绝对可以大大提升我们的效率。 正则表达式&#xff08;regular expression&#xff09;其实就是对字符串进行模式匹配的技术。 快速入门 我们这里…...

编程日记 2023/8/15 7:55:20

ThreadLocal源码解析

使用ThreadLocal可以为每个线程维护一个线程变量&#xff0c;使用场景为线程间隔离&#xff0c;线程内方法共享&#xff1b; 原理&#xff1a; Thread类中有一个实例属性ThreadLocalMap&#xff0c;ThreadLocalMap中存放的是Entry数组&#xff0c;Entry数组是ThreadLocal和Ob…...

编程日记 2023/8/15 7:54:18

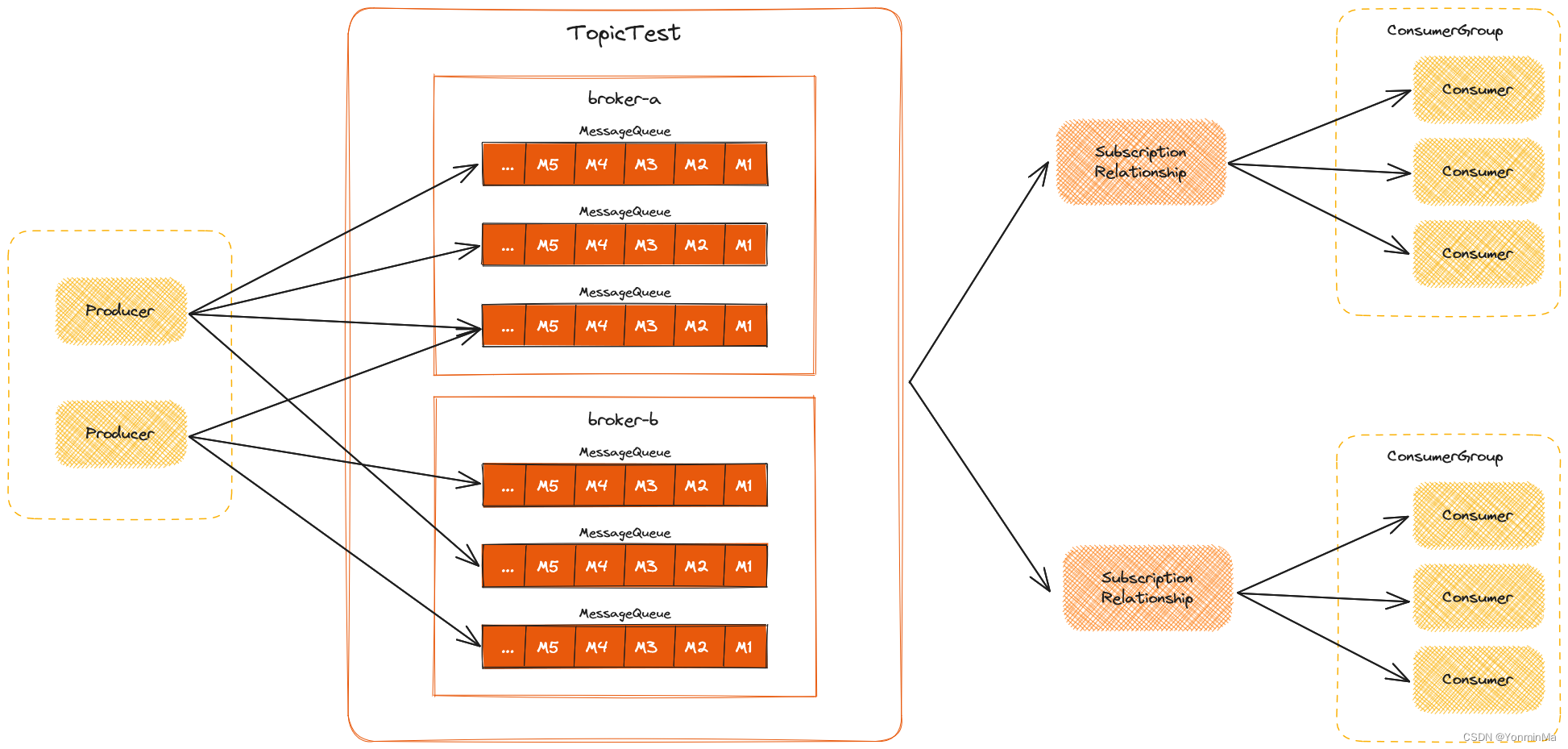
RocketMQ 5.1.0 源码详解 | Producer 发送流程

文章目录 初始化DefaultMQProducer实例发送流程DefaultMQProducer#sendDefaultMQProducerImpl#sendMQClientInstance#updateTopicRouteInfoFromNameServer使用特定 topic 获取路由信息使用默认 topic 获取路由信息 DefaultMQProducerImpl#sendDefaultImpl发送流程总结 初始化De…...

编程日记 2023/8/15 7:53:17

电脑ip地址怎么改 ip地址怎么改到别的城市

一、ip地址怎么改到别的城市 1.ip地址怎么改到别的城市&#xff0c;1、重启WIFI路由设备 一般手机或电脑在家或公司上网时都是接入到路由器的WIFI网络,再由路由器分配上网IP地址,如果要更换上网IP那么重启路由器设备后,路由器会向网络运营商进行宽带的重新拨号,此时手机或电脑设…...

编程日记 2023/8/15 7:52:16

Android Studio实现列表展示图片

效果&#xff1a; MainActivity 类 package com.example.tabulation;import android.content.Intent; import android.os.Bundle; import android.view.View;import androidx.appcompat.app.AppCompatActivity; import androidx.recyclerview.widget.LinearLayoutManager; im…...

编程日记 2023/8/15 7:51:15

每天一道leetcode：300. 最长递增子序列（动态规划中等）

今日份题目&#xff1a; 给你一个整数数组 nums &#xff0c;找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列&#xff0c;删除&#xff08;或不删除&#xff09;数组中的元素而不改变其余元素的顺序。例如&#xff0c;[3,6,2,7] 是数组 [0,3,1,6,2,2,7] …...

编程日记 2023/8/15 7:50:13

【无监督】2、MAE | 自监督模型提取的图像特征也很能打！（CVPR2022 Oral）

文章目录 一、背景二、方法三、效果 论文&#xff1a;Masked Autoencoders Are Scalable Vision Learners 代码&#xff1a;https://github.com/facebookresearch/mae 出处&#xff1a;CVPR2022 Oral | 何凯明 | FAIR 一、背景 本文的标题突出了两个词&#xff1a; masked…...

编程日记 2023/8/15 7:49:12

pytorch单机多卡后台运行

nohup sh ./train_chat.sh > train_chat20230814.log 2>1&参考资料 Pytorch单机多卡后台运行的解决办法...

编程日记 2023/8/15 7:48:11

linux配置上网 linux adsl拨号上网设置

Linux里面配置ADSL上网是件很麻烦的事。但配置完成之后就能开机自动拨号上网&#xff0c;可谓十分的方便。支持的系统有Redhat,CentOS,SuSE,FreeBSD,Ubuntu等常见的Linux。 工具/原料 ADSL网络&#xff0c;电信&#xff0c;网通&#xff0c;移动等常见宽带。 Linux系统的安装光…...

编程日记 2023/8/15 7:47:10

XML学习基础知识归纳(一)

一、XML基本概述 &#xff08;1&#xff09;概念&#xff1a;XML是可扩展的标记语言&#xff0c;xml文档的后缀名为 .xml &#xff08;2&#xff09;作用&#xff1a;用来用来传输和存储数据&#xff0c;不用于表现和展示数据&#xff0c;这点呢相比于HTML来说是不同的&#…...

编程日记 2023/8/15 7:46:09

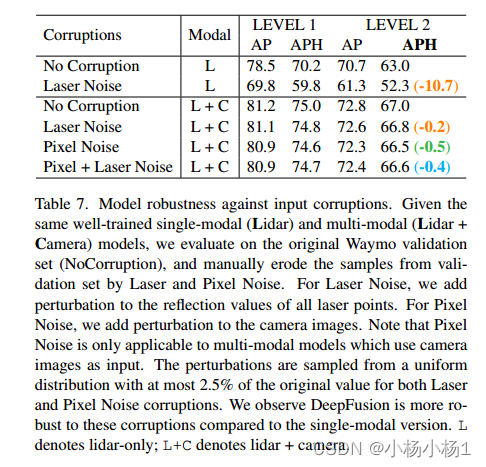
2023.8.14论文阅读

文章目录 ESPNet: Efficient Spatial Pyramid of Dilated Convolutions for Semantic Segmentation摘要本文方法实验结果 DeepFusion: Lidar-Camera Deep Fusion for Multi-Modal 3D Object Detection摘要本文方法实验结果 ESPNet: Efficient Spatial Pyramid of Dilated Convo…...

编程日记 2023/8/15 7:45:08

FL Studio for Windows-21.1.0.3713中文直装版功能介绍及系统配置要求

FL Studio 21简称FL水果软件,全称是&#xff1a;Fruity Loops Studio编曲&#xff0c;由于其Logo长的比较像一款水果因此&#xff0c;在大家更多的是喜欢称他为水果萝卜&#xff0c;FL studio21是目前最新的版本&#xff0c;这是一款可以让你的计算机就像是一个全功能的录音室&…...

编程日记 2023/8/15 7:44:06

基于网格变形的二维图像变形算法：C++实现与应用

在计算机图形学中&#xff0c;图像变形是一种常见的技术&#xff0c;它可以改变图像的形状和结构&#xff0c;以满足特定的视觉效果或者应用需求。本文将介绍一种基于网格变形的二维图像变形算法&#xff0c;并使用C进行实现。 一、算法原理 网格变形是一种基于网格的图像变形…...

编程日记 2023/8/15 7:43:05

【数据结构】八大排序详解

&#x1f680; 作者简介&#xff1a;一名在后端领域学习&#xff0c;并渴望能够学有所成的追梦人。 &#x1f40c; 个人主页&#xff1a;蜗牛牛啊 &#x1f525; 系列专栏&#xff1a;&#x1f6f9;数据结构、&#x1f6f4;C &#x1f4d5; 学习格言&#xff1a;博观而约取&…...

编程日记 2023/8/15 7:42:04

VSCode如何设置高亮

一、概述 本文主要介绍在 VSCode 看代码时&#xff0c;怎样使某个单词高亮显示&#xff0c;主要通过以下三步实现&#xff1a; 安装 highlight-words 插件 配置 highlight-words 插件 设置高亮快捷键F8 工作是嵌入式开发的&#xff0c;代码主要是C/C的&#xff0c;之前一直用…...

编程日记 2023/8/15 7:41:03

密钥大全ubuntu

VMware Workstation Tech Preview 20H2 GG1JR-APD1P-0857Q-DQQN9-PU2CA VMware Workstation v16 Pro for Windows&#xff08;反馈失效&#xff09; ZF3R0-FHED2-M80TY-8QYGC-NPKYF YF390-0HF8P-M81RQ-2DXQE-M2UT6 ZF71R-DMX85-08DQY-8YMNC-PPHV8 VMware Workstation v15 f…...

编程日记 2023/8/15 7:40:02

Spring Task入门案例

Spring Task 是Spring框架提供的任务调度工具&#xff0c;可以按照约定的时间自动执行某个代码逻辑。 定位&#xff1a;定时任务框架 作用&#xff1a;定时自动执行某段Java代码 强调&#xff1a;只要是需要定时处理的场景都可以使用Spring Task 1. cron表达式 cron表达式…...

编程日记 2023/8/15 7:39:01

针对Android项目蓝牙如何学习

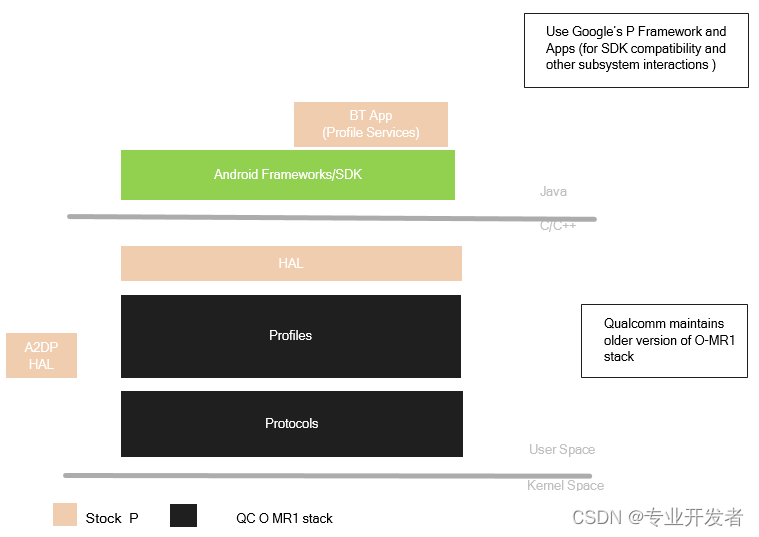
一、概述（Overview） 蓝牙是一种专有的开放式无线技术标准，用于在固定和移动设备之间进行短距离数据交换（使用2400–2480 MHz ISM波段的短波长无线电传输），从而创建具有高度安全性的个人局域网（PANs）。由电信供应商爱立信（telecoms vendor Ericsson）于1994年创建，[1…...

编程日记 2023/8/15 7:38:00

C++学习笔记总结练习：内存分配器编程实现

内存分配器练习 C内存分配器是用于管理程序运行时内存的工具。它负责分配和释放内存&#xff0c;以满足程序在运行过程中的动态内存需求。在C中&#xff0c;有几种内存分配器可供选择&#xff0c;包括操作系统提供的默认分配器、自定义分配器和第三方库提供的分配器。 默认分配…...

编程日记 2023/8/15 7:36:59

Sentinel-3B OLCI 3 级全球分箱地球观测降分辨率（ERR）叶绿素（CHL）数据，版本 2022.0

Sentinel-3B OLCI Level-3 Global Binned Earth-observation Reduced Resolution (ERR) Chlorophyll (CHL) Data, version 2022.0 简介 叶绿素 a 数据集提供全球网格化的表层叶绿素 a 浓度&#xff08;浮游植物生物量的替代指标&#xff09;合成数据。CHL 支持时间序列和气候…...

编程新知 2026/5/26 3:20:03

如何删除论文脚注横线的方法——视图-草稿-引用——显示备注——删除脚注分隔符-即可。

如何删除论文脚注横线的方法——视图-草稿-引用——显示备注——删除脚注分隔符-即可。 Word中脚注线不会删&#xff1f;这里有妙招&#xff01;,教育,职业教育,好看视频...

编程新知 2026/5/26 3:15:58

Rydberg原子量子门实现原理与优化技术

1. Rydberg原子平台中的量子门实现基础1.1 Rydberg原子特性与量子计算优势Rydberg原子是指外层电子被激发到高主量子数能级的原子态&#xff0c;这类原子具有三个关键特性使其成为量子计算的理想平台&#xff1a;强偶极-偶极相互作用&#xff1a;当两个原子同时处于Rydberg态时…...

编程新知 2026/5/26 3:05:50

智能检索新范式，让AIAgent自主决策，提升RAG效率100%！

市面上的 RAG 系统&#xff0c;不管叫什么名字&#xff0c;本质上只有两种做法&#xff1a; 第一种&#xff0c;一次性检索。把用户的 query 向量化&#xff0c;从语料库里捞出 Top-K 个文档片段&#xff0c;拼成一个大 prompt 塞给模型。GraphRAG、HippoRAG、LightRAG 都属于…...

编程新知 2026/5/26 2:55:48

为Alchitry Au FPGA开发板外接JTAG接口的完整指南

1. 项目概述与核心价值如果你正在使用基于Xilinx Artix-7 FPGA的Alchitry Au或Au开发板&#xff0c;并且已经厌倦了每次调试或烧录都要依赖板载的USB-JTAG桥接芯片&#xff0c;或者你的项目已经将板载USB接口挪作他用&#xff0c;那么为你的开发板外接一个独立的JTAG调试器&…...

编程新知 2026/5/26 2:05:15

Python基础语法：常用内置函数

round()&#xff1a;四舍五入 # 省略 ndigits print(round(3.14)) # 输出 3&#xff08;int&#xff09; print(round(3.66)) # 输出 4# 指定 ndigits print(round(3.14159, 2)) # 输出 3.14&#xff08;float&#xff09; print(round(3.666, 2)) # 输出 3.67# …...

编程新知 2026/5/26 1:29:07

我靠这个测试设计方法，把漏测率降低了80%

当“直觉测试”撞上南墙很长一段时间里&#xff0c;我和许多测试同行一样&#xff0c;测试用例的设计主要依靠两样东西&#xff1a;需求文档和“测试直觉”。这种模式在业务逻辑相对简单、迭代速度平缓时还能勉强应付。一旦面对复杂的企业级应用、高频的敏捷迭代&#xff0c;或…...

编程新知 2026/5/26 0:40:30

Sangfor文件夹可以删除吗？【图文讲解】深信服文件夹残留清理？如何彻底删除深信服？Sangfor文件夹是什么？

&#xff08;1&#xff09;问题背景打开C盘&#xff0c;突然冒出个Sangfor 文件夹&#xff0c;占用好几个 GB 空间&#xff0c;想删又不敢删&#xff0c;怕删坏系统、断网崩溃&#xff1b;上网一查&#xff0c;说法五花八门&#xff0c;有人说是病毒&#xff0c;有人说是办公软…...

编程新知 2026/5/26 0:16:08

如何进行TVA仿真引擎的“光照地狱”训练？

重磅预告&#xff1a;本专栏将独家连载系列丛书《智能体视觉技术与应用》部分精华内容&#xff0c;该书是世界首套系统阐述“因式智能体”视觉理论与实践的专著&#xff0c;特邀美国 TypeOne 公司首席科学家、斯坦福大学博士 Bohan 担任技术顾问。Bohan先生师从美国三院院士、“…...

编程新知 2026/5/26 0:05:58

Godot4 2D游戏开发避坑指南：TileMap绘制、节点顺序与相机设置的三个常见问题

Godot4 2D游戏开发避坑指南&#xff1a;TileMap绘制、节点顺序与相机设置的三个常见问题当你第一次用Godot4完成一个2D场景搭建时&#xff0c;那种成就感往往会被几个突如其来的bug瞬间击碎——角色神秘消失、背景纹丝不动、屏幕边缘出现诡异黑边。这些问题看似简单&#xff0c…...

编程新知 2026/5/25 23:18:53