2023年国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
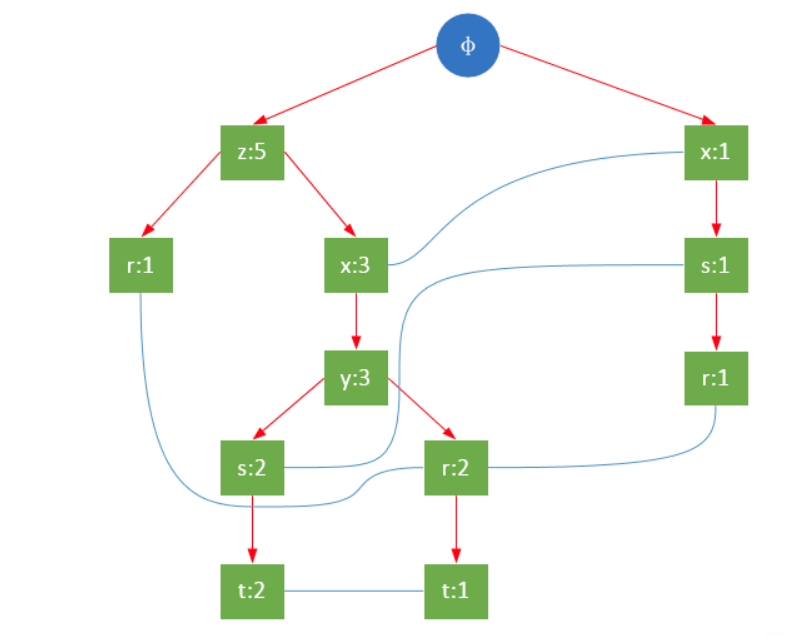
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
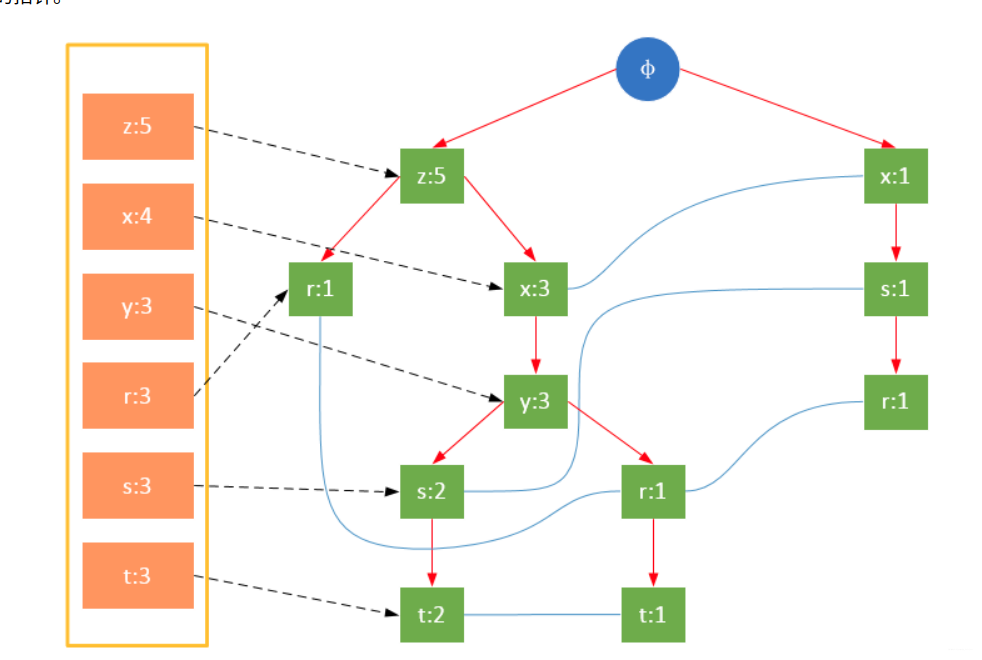
3 构建FP树
现在有如下数据:
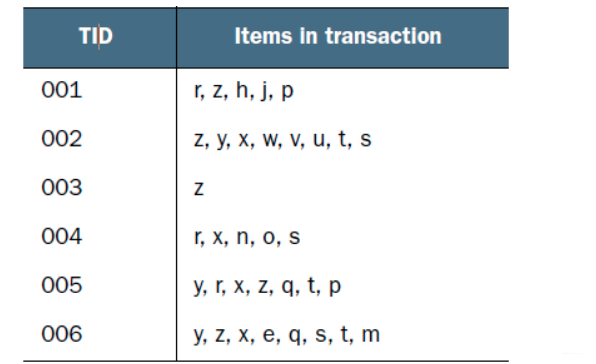
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
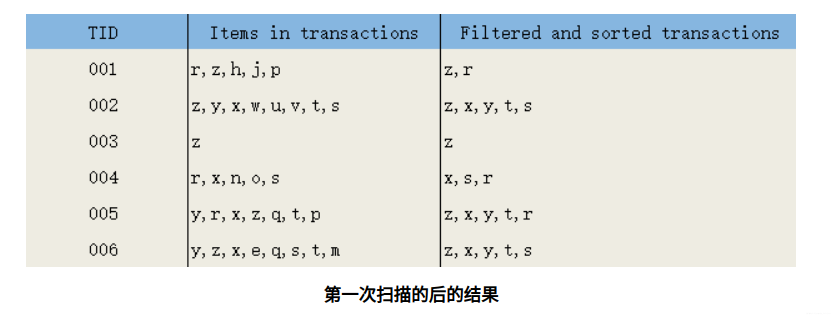
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
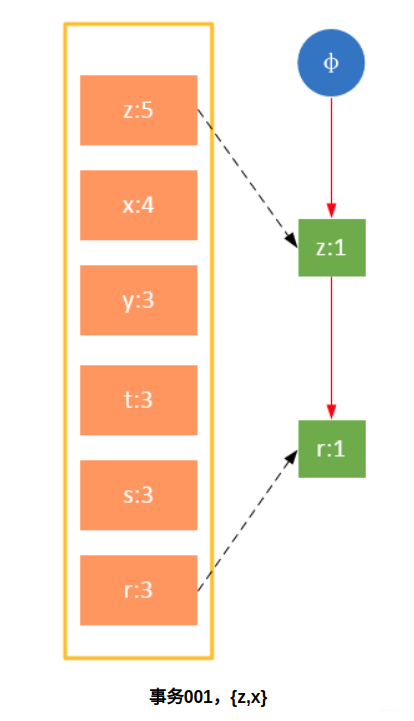
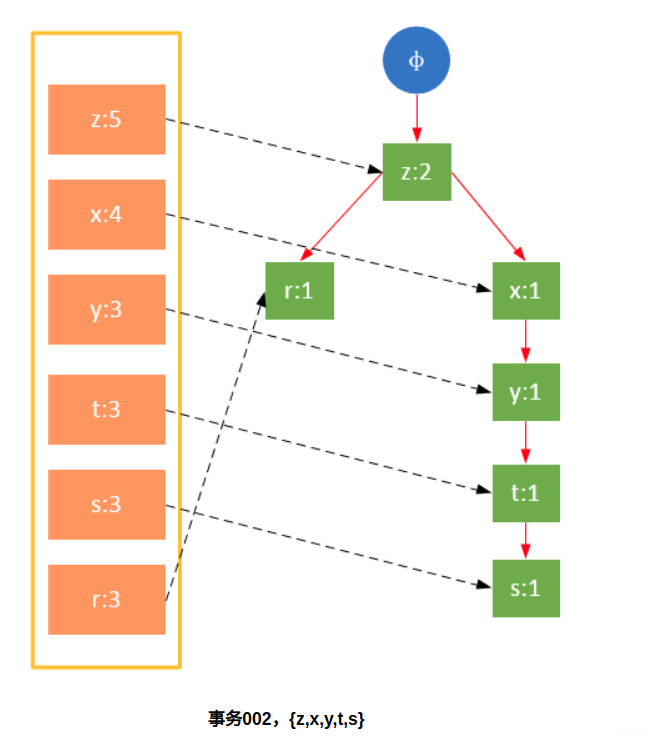
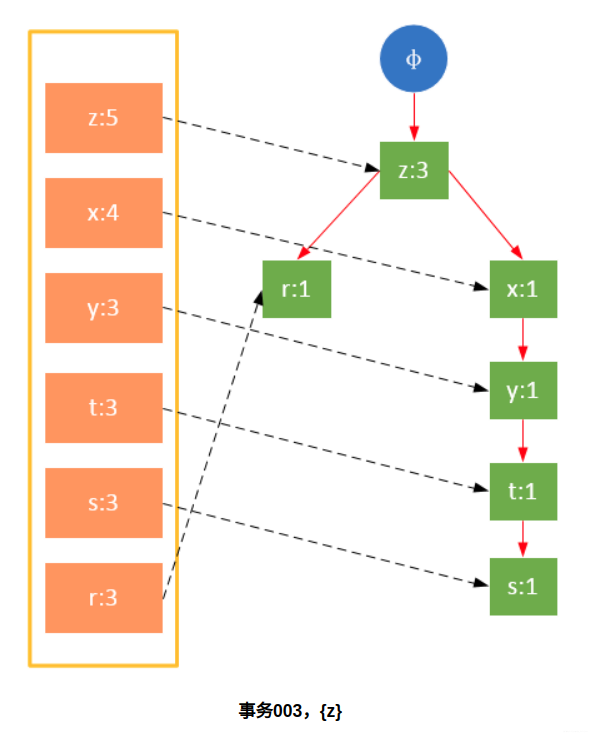
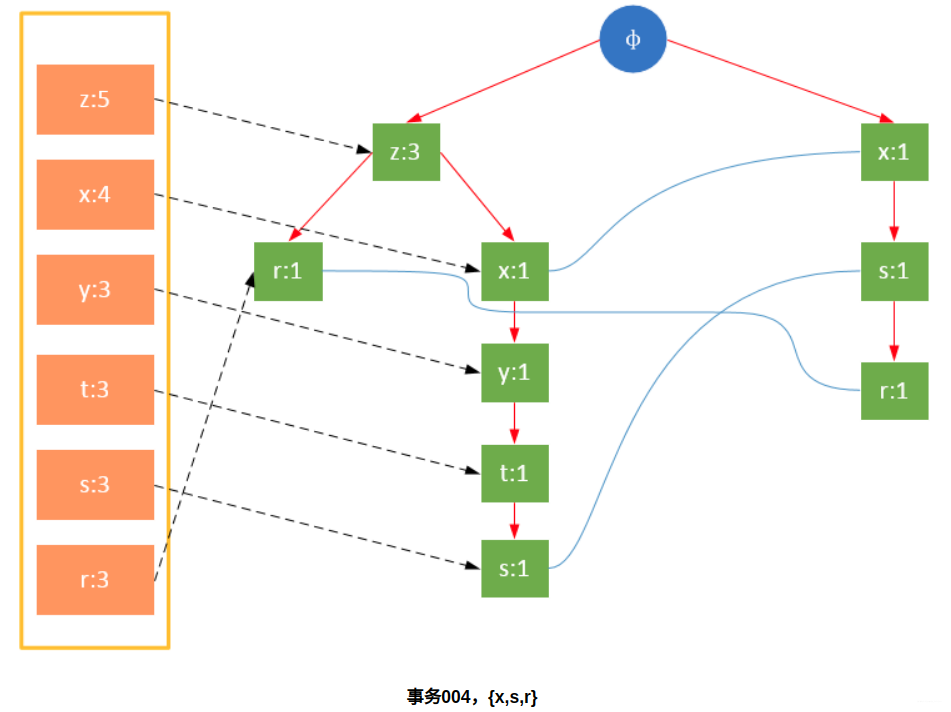
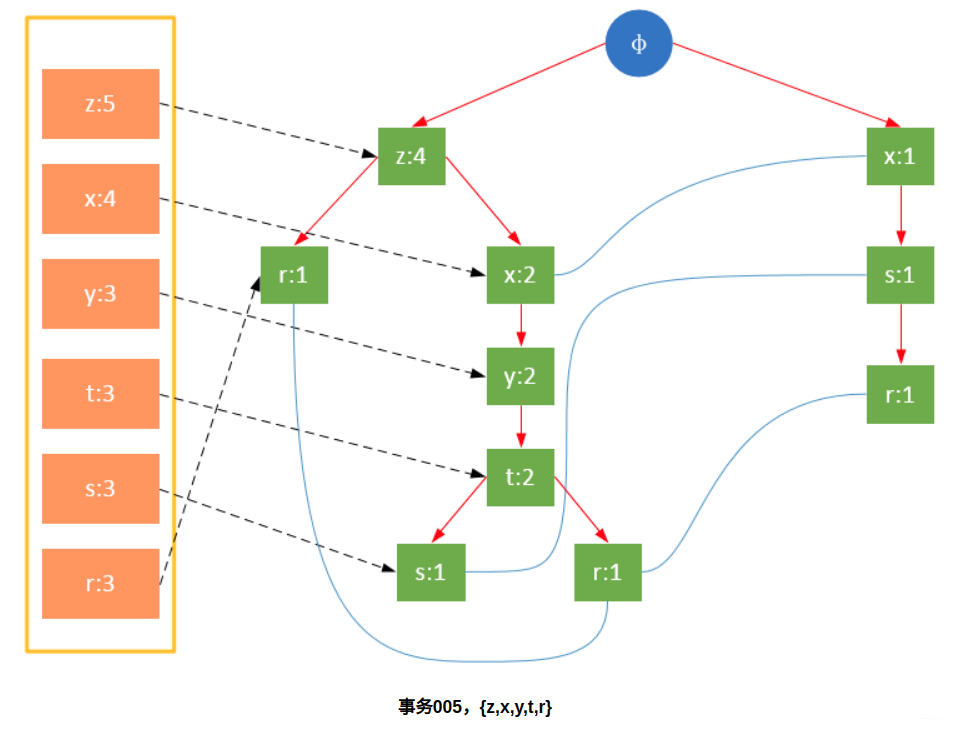
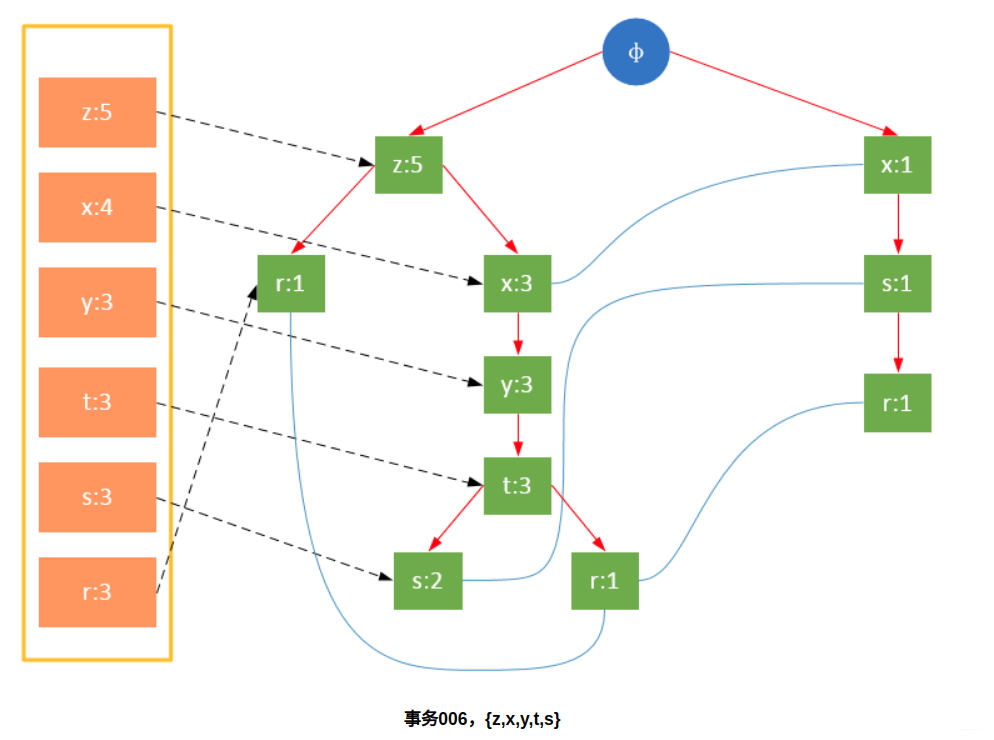
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023年国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
-三维堆积柱形图(3D Stacked Bar Chart))
可视化绘图技巧100篇进阶篇(七)-三维堆积柱形图(3D Stacked Bar Chart)
目录 前言 适用场景 图例 绘图工具及代码实现 HighCharts echarts MATLAB...

React源码解析18(7)------ 实现事件机制(onClick事件)
摘要 在上一篇中,我们实现了useState的hook,但由于没有实现事件机制,所以我们只能将setState挂载在window上。 而这一篇主要就是来实现事件系统,从而实现通过点击事件进行setState。 而在React中,虽然我们是将事件绑…...
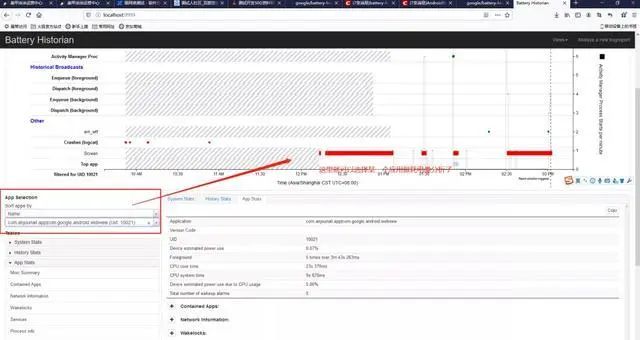
Android app专项测试之耗电量测试
前言 耗电量指标 待机时间成关注目标 提升用户体验 通过不同的测试场景,找出app高耗电的场景并解决 01、需要的环境准备 1、python2.7(必须是2.7,3.X版本是不支持的) 2、golang语言的开发环境 3、Android SDK 此三个的环境搭建这里就不详细说了&am…...

设计模式-面试常问
1.单例模式 保证系统中,一个类,只有一个实例,并且提供对外访问。 优点:只有一个对象,可以节省资源。适合频繁创建销毁对象的场景。 实现:要用到static,静态私有对象。暴露单例的静态方法。 &…...
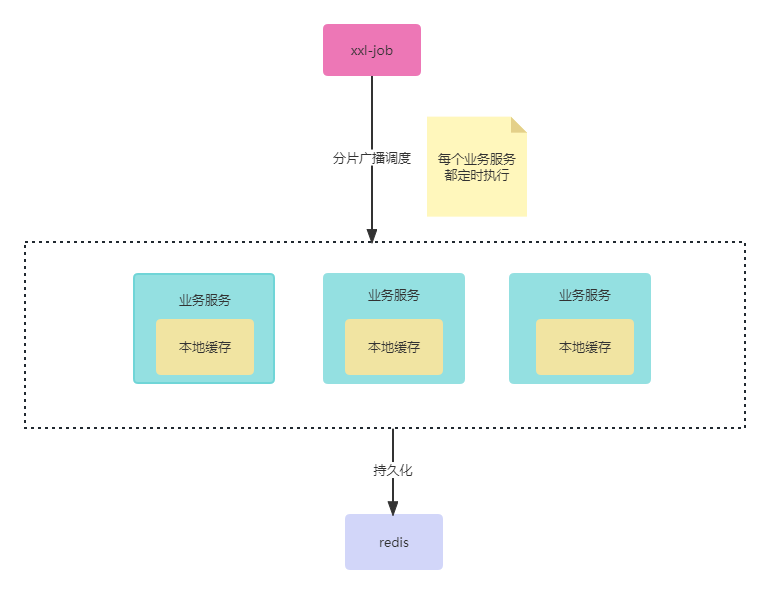
聊聊在集群环境中本地缓存如何进行同步
前言 之前有发过一篇文章聊聊如何利用redis实现多级缓存同步。有个读者就给我留言说,因为他项目的redis版本不是6.0版本,因此他使用我文章介绍通过MQ来实现本地缓存同步,他的同步流程大概如下图 他原来的业务流程是每天凌晨开启定时器去爬取…...
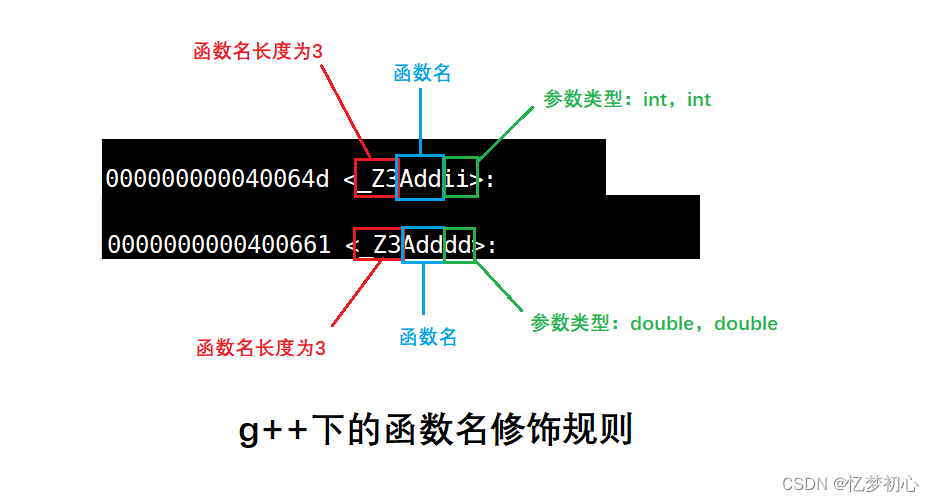
【C++深入浅出】初识C++上篇(关键字,命名空间,输入输出,缺省参数,函数重载)
目录 一. 前言 二. 什么是C 三. C关键字初探 四. 命名空间 4.1 为什么要引入命名空间 4.2 命名空间的定义 4.3 命名空间使用 五. C的输入输出 六. 缺省参数 6.1 缺省参数的概念 6.2 缺省参数的分类 七. 函数重载 7.1 函数重载的概念 7.2 函数重载的条件 7.3 C支…...

租房合同范本
房屋租赁合同 甲方(出租方): 身份证: 联系电话: 乙方(承租方): 身份证: 联系电话: …...

轻薄的ESL电子标签有哪些特性?
在智慧物联逐渐走进千万家的当下,技术变革更加日新月异。ESL电子标签作为科技物联的重要组成部分,是推动千行百业数字化转型的重要技术,促进物联网产业的蓬勃发展。在智慧零售、智慧办公、智慧仓储等领域,ESL电子标签在未来是不可…...

AI 实力:利用 Docker 简化机器学习应用程序的部署和可扩展性
利用 Docker 的强大功能:简化部署解决方案、确保可扩展性并简化机器学习模型的 CI/CD 流程。 近年来,机器学习 (ML) 出现了爆炸性增长,导致对健壮、可扩展且高效的部署方法的需求不断增加。由于训练和服务环境之间的差异或扩展的困难等因素&a…...
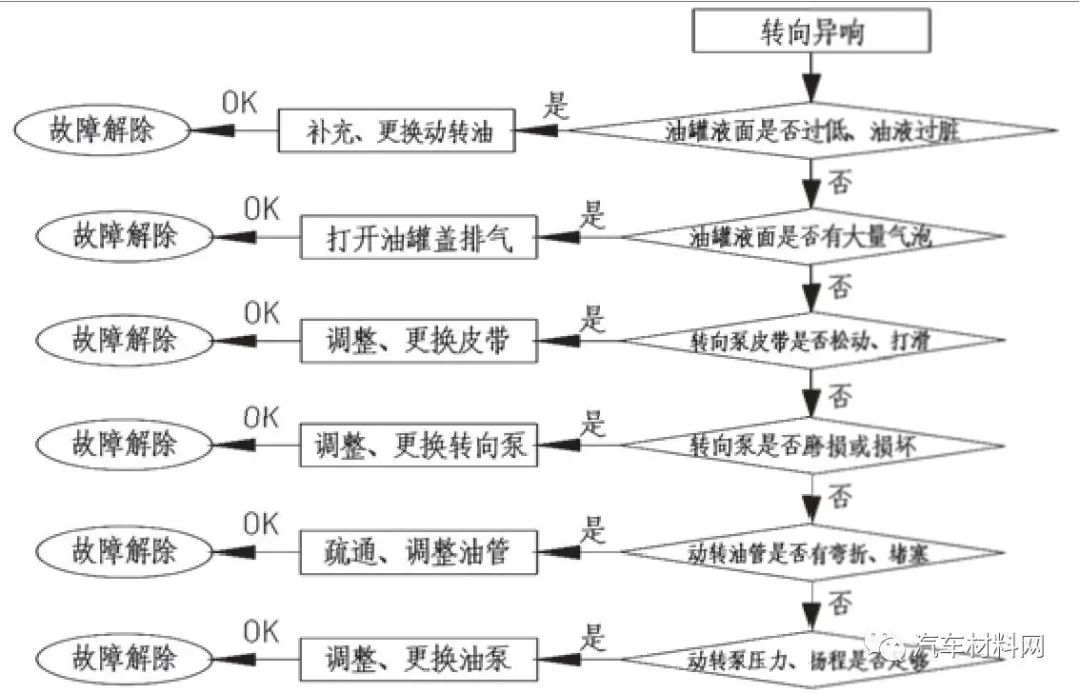
商用汽车转向系统常见故障解析
摘要: 车辆转向系统是用于改变或保持汽车行驶方向的专门机构。其作用是使汽车在行驶过程中能按照驾驶员的操纵意图而适时地改变其行驶方向,并在受到路面传来的偶然冲击及车辆意外地偏离行驶方向时,能与行驶系统配合共同保持车辆继续稳定行驶…...

Python中的MetaPathFinder
MetaPathFinder 是 Python 导入系统中的一个关键组件,它与 sys.meta_path 列表紧密相关。sys.meta_path 是一个包含 MetaPathFinder 实例的列表,这些实例用于自定义模块的查找和加载逻辑。当使用 import 语句尝试导入一个模块时,Python 会遍历…...

工控机防病毒
2月3日,作为全球最大的半导体制造设备和服务供应商,美国应用材料公司(Applied Materials)表示,有一家上游供应商遭到勒索软件攻击,由此产生的关联影响预计将给下季度造成2.5亿美元(约合人民币17…...
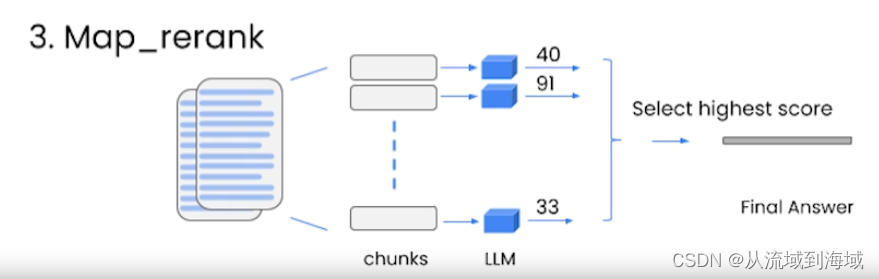
LangChain手记 Question Answer 问答系统
整理并翻译自DeepLearning.AILangChain的官方课程:Question Answer(源代码可见) 本节介绍使用LangChian构建文档上的问答系统,可以实现给定一个PDF文档,询问关于文档上出现过的某个信息点,LLM可以给出关于该…...

如何优化css中的一些昂贵属性
如何优化css中的一些昂贵属性 就性能而言,某些 CSS 属性比其他属性的成本更高。如果使用不当,它们可能会减慢我们的网页速度并降低对用户的响应速度。在本文中,我们将探讨一些成本最高的 CSS 属性以及如何优化它们。 box-shadow box-shado…...
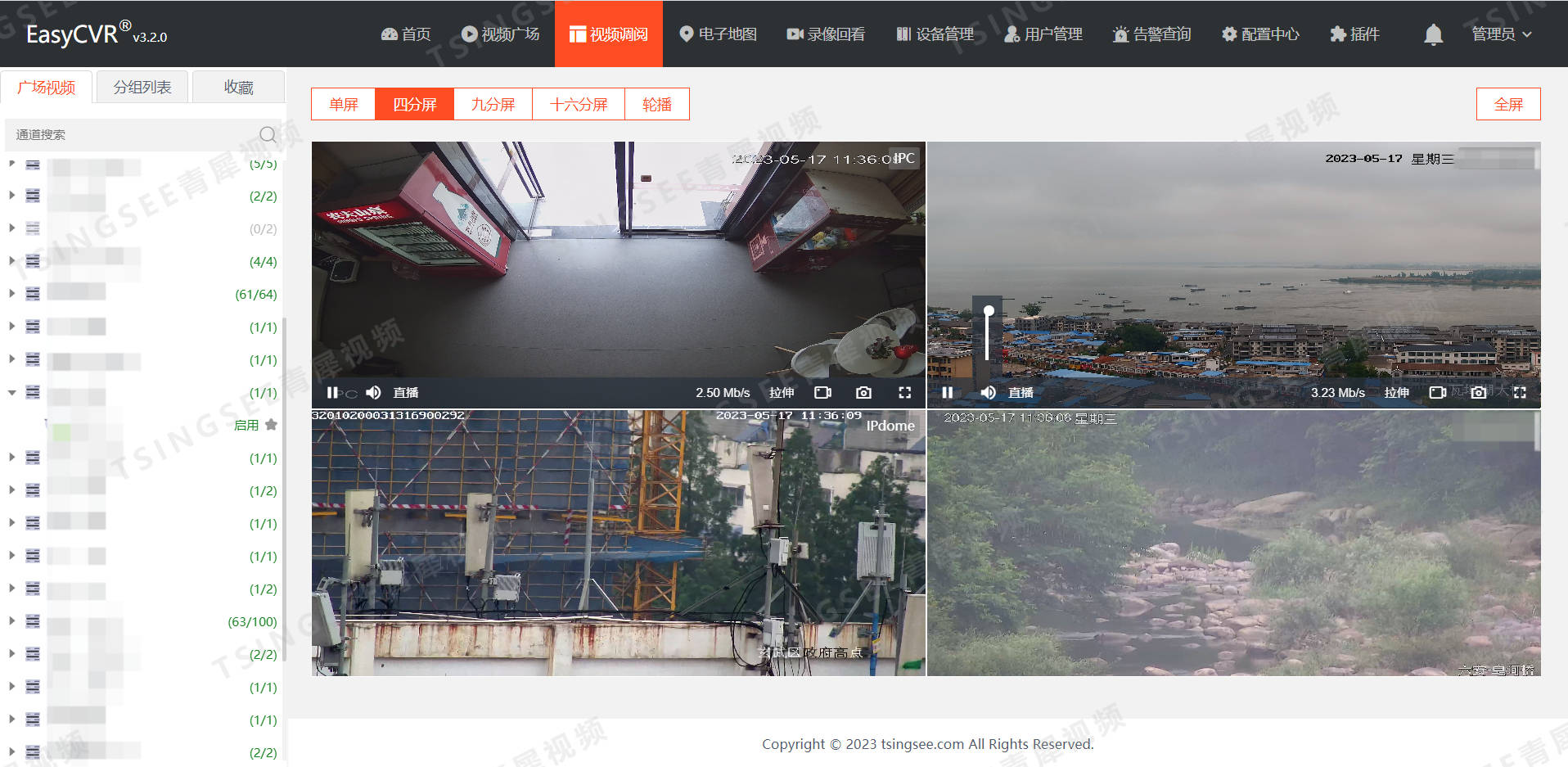
基于安防监控EasyCVR视频汇聚融合技术的运输管理系统的分析
一、项目背景 近年来,随着物流行业迅速发展,物流运输费用高、运输过程不透明、货损货差率高、供应链协同能力差等问题不断涌现,严重影响了物流作业效率,市场对于运输管理数字化需求愈发迫切。当前运输行业存在的难题如下…...
)
在WordPress站点中展示阅读量等流量分析数据(超详细实现)
这篇文章也可以在我的博客中查看 关于本文 专业的流量统计系统能够相对真实地反应网站的访问情况。 这些数据可以在后台很好地进行分析统计,但有时我们希望在网站前端展示一些数据 最常见的情景就是:展示页面的浏览量 这简单的操作当然也可以通过简单…...
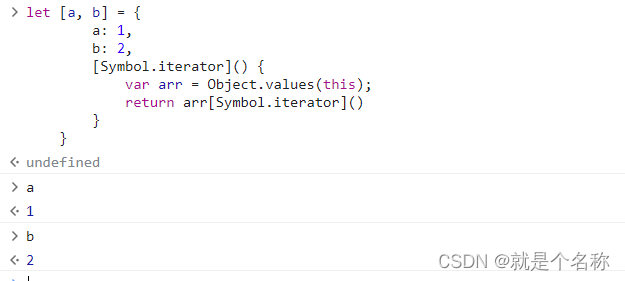
学习 Iterator 迭代器
今天看到一个面试题, 让下面解构赋值成立。 let [a,b] {a:1,b:2} 如果我们直接在浏览器输出这行代码,会直接报错,说是 {a:1,b:2} 不能迭代。 看了es6文档后,具有迭代器的就一下几种类型,没有Object类型,…...

JVM---垃圾回收算法介绍
目录 分代收集理论 三种垃圾回收算法 标记-清除算法(最基础的、基本不用) 标记-复制算法 标记-整理算法 正式因为jvm有了垃圾回收机制,作为java开发者不会去特备关注内存,不像C和C。 优点:开发门槛低、安全 缺点…...
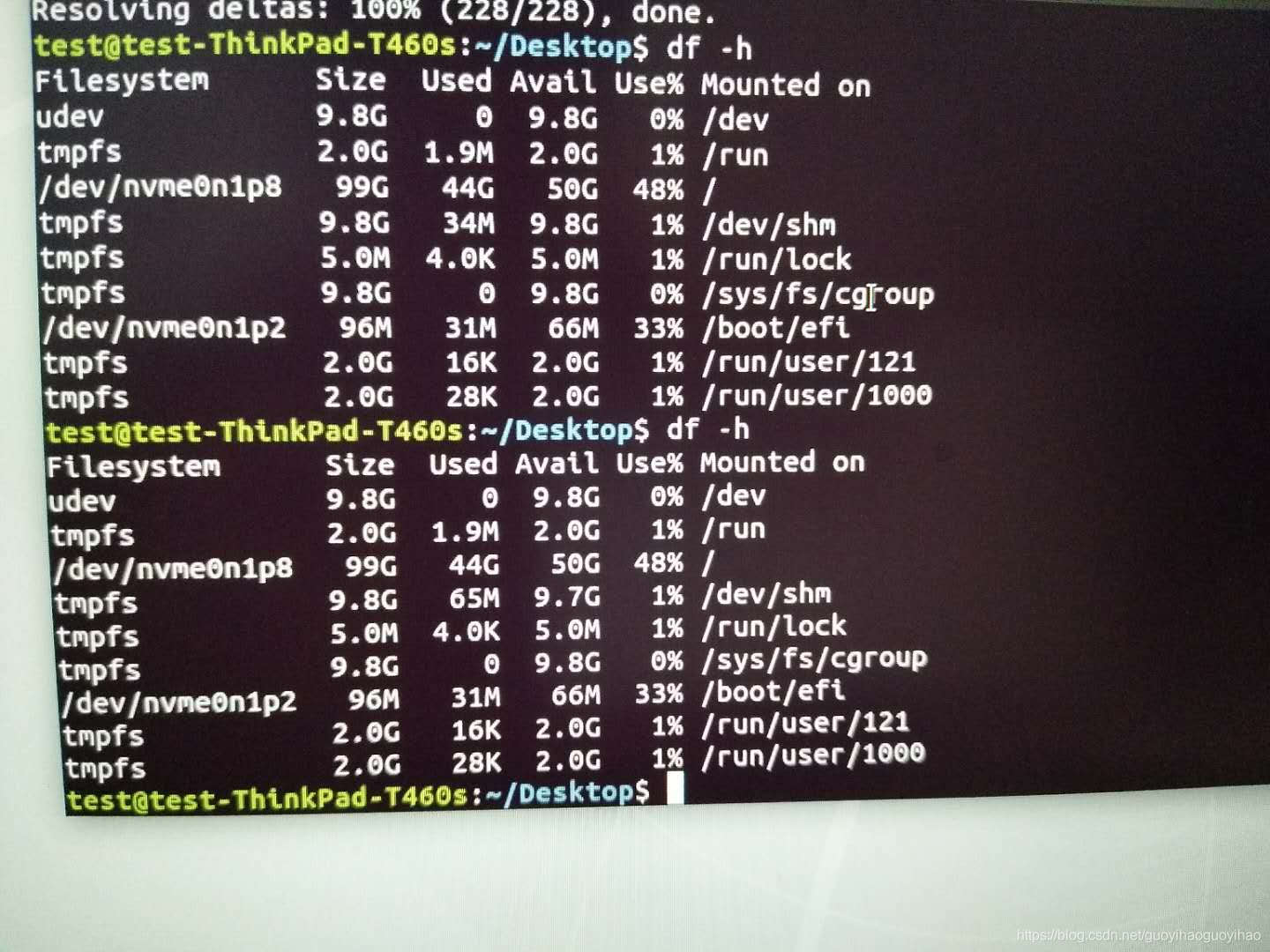
Ubuntu一直卡死的问题(20.04)
Ubuntu一直卡死的问题(18.04)_ubuntu频繁死机_Mr.Yi的博客-CSDN博客 我自己的解决方法: 1、首先强制关机重启后,直接打开命令行查看磁盘的使用: df -h发现/dev/loop都沾满了,我们能需要做的就是把他们清理干净 sud…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
