凸优化基础学习——凸集
凸优化基础学习——凸集
文章内容全部来自对Stephen Boyd and Lieven vandenberghe的Convex Optimization的总结归纳。
电子书资源:
链接:https://pan.baidu.com/s/1dP5zI6h3BEyGRzSaJHSodg?pwd=0000
提取码:0000
基本概念
仿射集合
**仿射集合:**通过集合 C ⊆ R n C\subseteq \mathbf{R}^n C⊆Rn中任意两个不同点的直线仍然在集合 C C C中,则称集合 C C C是仿射的。
另一种等价定义:对于任意 x 1 , x 2 ∈ C x_1,x_2\in C x1,x2∈C及 θ ∈ R \theta\in\mathbf{R} θ∈R有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+\left( 1-\theta \right) x_2\in C θx1+(1−θ)x2∈C,即 C C C中包含了 C C C中任意两点的系数之和为1的线性组合。
**仿射组合:**仿射集合的概念可以扩展到多个点的情况,如果 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1,那么具有 θ 1 x 1 + ⋯ + θ k x 1 = 1 \theta_1x_1+\cdots+\theta_kx_1=1 θ1x1+⋯+θkx1=1形式的点为 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的仿射组合。
**仿射包:**集合 C ⊆ R n C\subseteq\mathbf{R}^n C⊆Rn中的点的所有仿射组合组成的集合为 C C C的仿射包,记作 a f f C : \mathbf{aff}C: affC:
**仿射维数:**定义集合 C C C的仿射维数为其仿射包的维数。
a f f C = { θ 1 x 1 + ⋯ + θ k x k ∣ x 1 , ⋯ , x k ∈ C , θ 1 + ⋯ + θ k = 1 } \mathbf{aff}C=\{\theta_1x_1+\cdots+\theta_kx_k|x_1,\cdots,x_k\in C,\theta_1+\cdots+\theta_k=1\} affC={θ1x1+⋯+θkxk∣x1,⋯,xk∈C,θ1+⋯+θk=1}
性质:
- 仿射集合 C C C可以表示成
C = V + x 0 = v + x 0 ∣ v ∈ V C=V+x_0={v+x_0|v\in V} C=V+x0=v+x0∣v∈V
其中 C C C是一个子空间,并且关于加法和数乘是封闭的。 x 0 x_0 x0是 C C C中任意一点。**仿射集合 C C C**的维数定义为子空间 V = C − x 0 V=C-x_0 V=C−x0的维度。
- 一个仿射集合包含其中任意点的仿射组合,即如果 C C C是一个仿射集合, x 1 , ⋯ , x k ∈ C x_1,\cdots,x_k\in C x1,⋯,xk∈C,并且 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1,那么 θ 1 x 1 + ⋯ + θ k x k \theta_1x_1+\cdots+\theta_kx_k θ1x1+⋯+θkxk仍然在 C C C中。
- 仿射包是包含 C C C的最小仿射集合。
常见例子
- 线性方程组 C = { x ∣ A x = b } C=\{x|Ax=b\} C={x∣Ax=b}的解集是一个仿射集合,其子空间就是 A A A的零空间。同时任意仿射集合可以表示成一个线性方程组的解集。
凸集
**凸集:**如果 C C C中任意两点间的线段仍然在 C C C中,及对于任意 x 1 , x 2 ∈ C x_1,x_2\in C x1,x2∈C和满足 0 ≤ θ ≤ 1 0\le\theta\le1 0≤θ≤1的 θ \theta θ都有
θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+(1 - \theta)x_2\in C θx1+(1−θ)x2∈C
或者说如果集合中的每一个点都可以被其他的点沿着它们之间的一条无阻碍(整条路径都在集合中)的路径看见,那么这个集合就被称为凸集。
**凸组合:**称 θ 1 x 1 + ⋯ + θ k x 1 \theta_1x_1+\cdots+\theta_kx_1 θ1x1+⋯+θkx1为点 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的一个凸组合,其中 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1并且 θ i ≥ 0 , i = 1 , ⋯ , k 。 \theta_i\ge0,i=1,\cdots,k。 θi≥0,i=1,⋯,k。
**凸包:**集合 C C C中所有点构成的凸组合的集合为其凸包,记为 conv C : \text{\textbf{conv}}C: convC:
conv C = { θ 1 x 1 + ⋯ + θ k x k ∣ x i ∈ C , θ i ≥ 0 , i = 1 , ⋯ , k , θ 1 + ⋯ + θ k = 1 } \text{\textbf{conv}}C=\{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i\ge0,i=1,\cdots,k,\theta_1+\cdots+\theta_k=1\} convC={θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k,θ1+⋯+θk=1}
性质:
- 仿射集是凸集。
- 一个集合的凸集等价于集合中包含了其中所有点的凸组合,可以理解为混合和加权平均。
- 凸包是包含集合 C C C的最小凸集,即有如果 B B B是包含 C C C的凸集,那么 conv C ⊆ B \text{\textbf{conv}}C\subseteq B convC⊆B。
锥
**锥:**如果对于任意 x ∈ C x\in C x∈C和 θ ≥ 0 \theta \ge0 θ≥0都有 θ x ∈ C \theta x\in C θx∈C,那么我们就称集合 C C C是锥或者说是非负齐次的。
**凸锥:**对于任意 x 1 , x 2 ∈ C x_1,x_2\in C x1,x2∈C和 θ 1 , θ 2 ≥ 0 , 都有 \theta_1,\theta_2\ge0,都有 θ1,θ2≥0,都有
θ 1 x 1 + θ 2 x 2 ∈ C \theta_1x_1+\theta_2x_2\in C θ1x1+θ2x2∈C
具有这类形式的点构成了二维的扇形
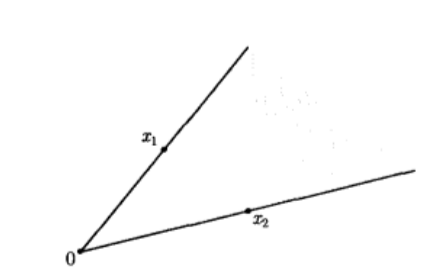
**锥组合(非负线性组合):**具有 θ 1 x 1 + ⋯ + θ k x 1 , θ 1 , ⋯ , θ k ≥ 0 \theta_1x_1+\cdots+\theta_kx_1,\theta_1,\cdots,\theta_k\ge0 θ1x1+⋯+θkx1,θ1,⋯,θk≥0形式的点称为 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的锥组合。
**锥包:**集合 C C C中元素的所有锥组合的集合,即
{ θ 1 x 1 + ⋯ + θ k x k ∣ x i ∈ C , θ i ≥ 0 , i = 1 , ⋯ , k } \{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i\ge0,i=1,\cdots,k\} {θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k}
性质
-
如果 x i x_i xi均属于凸锥 C C C,那么 x i x_i xi的每一个锥组合也在 C C C中。即集合 C C C是凸锥的充分必要条件是它包含其元素的所有锥组合。
-
锥包是包含 C C C的最小的凸锥。左图代表由点组成的一个集合 C C C的凸锥,右图代表由一块连续的区域组成的集合 C C C的凸锥。
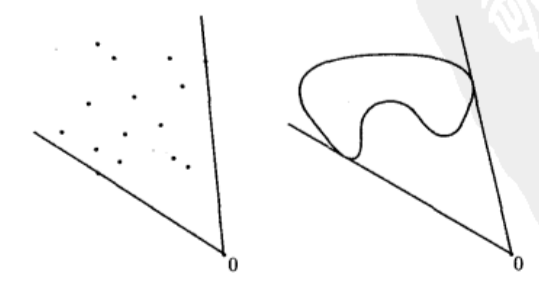
常见例子
简单例子
-
任意直线都是仿射的。如果直线通过零点,则是子空间,因此,也是凸锥。
-
一个线段是凸的,但不是仿射的(除非退化为一个点)。
-
空集、任意一个点、全空间 R n \mathbf{R}^n Rn都是 R n \mathbf{R}^n Rn的仿射(自然也是凸的)子集。
-
一条射线,既具有形式 { x 0 + θ v ∣ θ ≥ 0 } , v ≠ 0 \{x_0+\theta v|\theta\ge0\},v\neq0 {x0+θv∣θ≥0},v=0的集合,是凸的但不是仿射的。如果射线的基点 x 0 x_0 x0是0,则它是凸锥。
-
任意子空间是仿射的、凸锥。
超平面和半空间
**超平面:**具有以下形式的集合称为超平面
{ x ∣ a T x = b } \{x|a^Tx=b\} {x∣aTx=b}
其中 a ∈ R n , a ≠ 0 a\in \mathbf{R}^n,a\neq0 a∈Rn,a=0并且 b ∈ R b\in\mathbf{R} b∈R。显然超平面为关于 x x x的非平凡线性方程的解空间,因此其是一个仿射集合(当然也是凸集了)。
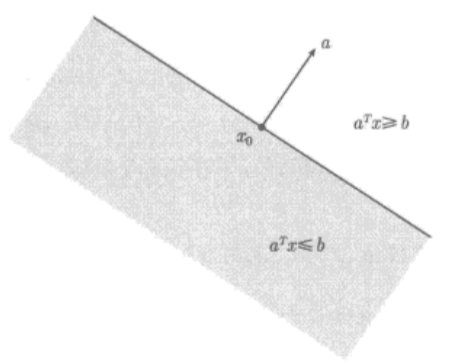
在几何上,超平面可以看作是和给定向量 a a a的内积为常数的点的集合;也可以看作是法线方向为 a a a的超平面,而常数 b ∈ R b\in\mathbf{R} b∈R决定了这个平面的偏移量。如下图所示

**半空间:**具有以下形式的集合称为半空间,其中 a ≠ 0 a\neq0 a=0,半空间是凸的,但不是仿射的。
{ x ∣ a T x ≤ b } \{x|a^Tx\le b\} {x∣aTx≤b}
**开半空间:**开半空间是半空间的内部,即具有以下形式的集合
{ x ∣ a T x < b } \{x|a^Tx< b\} {x∣aTx<b}
Euclid球和椭球
Euclid球: R n \mathbf{R}^n Rn中的Euclid球具有下面的形式,利用范数的三角不等式和齐次性可以证明它是凸集。
B ( x c , r ) = { x ∣ ∥ x − x c ∥ 2 ⩽ r } = { x ∣ ( x − x c ) T ( x − x c ) ⩽ r 2 } B\left(x_c, r\right)=\left\{x \mid\left\|x-x_c\right\|_2 \leqslant r\right\}=\left\{x \mid\left(x-x_c\right)^T\left(x-x_c\right) \leqslant r^2\right\} B(xc,r)={x∣∥x−xc∥2⩽r}={x∣(x−xc)T(x−xc)⩽r2}
其中 r > 0 r>0 r>0, ∥ ∥ 2 \left\|\right\|_2 ∥∥2表示Euclid范数, x c x_c xc表示球心,标量 r r r为半径。 B ( x c , r ) B\left(x_c, r\right) B(xc,r)为距离圆心 x c x_c xc距离不超过 r r r的所有点组成。
Euclid球的另外一种表达式如下
B ( x c , r ) = { x c + r u ∣ ∥ u ∥ 2 ⩽ 1 } B\left(x_c, r\right)=\left\{x_c+r u \mid\|u\|_2 \leqslant 1\right\} B(xc,r)={xc+ru∣∥u∥2⩽1}
**椭球:**具有以下形式的集合称为椭球,其同样为凸集
E = { x ∣ ( x − x c ) T P − 1 ( x − x c ) ⩽ 1 } \mathcal{E}=\left\{x \mid\left(x-x_c\right)^T P^{-1}\left(x-x_c\right) \leqslant 1\right\} E={x∣(x−xc)TP−1(x−xc)⩽1}
其中, P = P T ≻ 0 P=P^T\succ0 P=PT≻0,即 P P P为对称的正定矩阵。 x c x_c xc为椭圆中心,矩阵 P P P决定了椭球从 x c x_c xc向各个方向扩展的幅度。 E \mathcal{E} E的半轴长度由 λ i \sqrt{\lambda_i} λi决定,其中 λ i \lambda_i λi为 P P P的特征值。
椭球的另外一个表示形式为
E = { x c + A u ∣ ∥ u ∥ 2 ⩽ 1 } \mathcal{E}=\left\{x_c+A u \mid\|u\|_2 \leqslant 1\right\} E={xc+Au∣∥u∥2⩽1}
范数球和范数锥
**范数球:**定义如下,由范数的一般性质可以知道其为凸的
C = { ( x , t ) ∣ ∥ x ∥ ⩽ t } ⊆ R n + 1 C=\{(x, t) \mid\|x\| \leqslant t\} \subseteq \mathbf{R}^{n+1} C={(x,t)∣∥x∥⩽t}⊆Rn+1
**范数锥:**关于范数 ∥ ∥ \left\|\right\| ∥∥的范数锥是集合,其为一个凸锥
C = { ( x , t ) ∣ ∥ x ∥ ⩽ t } ⊆ R n + 1 C=\{(x, t) \mid\|x\| \leqslant t\} \subseteq \mathbf{R}^{n+1} C={(x,t)∣∥x∥⩽t}⊆Rn+1
**二阶锥:**由Euclid范数定义的范数锥称为范数锥,也可以称为二次锥、Lorentz锥或者冰淇淋锥。
C = { ( x , t ) ∈ R n + 1 ∣ ∥ x ∥ 2 ⩽ t } = { [ x t ] ∣ [ x t ] T [ I 0 0 − 1 ] [ x t ] ⩽ 0 , t ⩾ 0 } \begin{aligned} C & =\left\{(x, t) \in \mathbf{R}^{n+1} \mid\|x\|_2 \leqslant t\right\} \\ & =\left\{\left[\begin{array}{l} x \\ t \end{array}\right] \mid\left[\begin{array}{l} x \\ t \end{array}\right]^T\left[\begin{array}{cc} I & 0 \\ 0 & -1 \end{array}\right]\left[\begin{array}{l} x \\ t \end{array}\right] \leqslant 0, t \geqslant 0\right\} \end{aligned} C={(x,t)∈Rn+1∣∥x∥2⩽t}={[xt]∣[xt]T[I00−1][xt]⩽0,t⩾0}
下图是一个 R 3 \mathbf{R}^3 R3的二阶锥

多面体
**多面体:**定义为有限个线性等式和不等式的解集:
P = { x ∣ a j T x ⩽ b j , j = 1 , ⋯ , m , c j T x = d j , j = 1 , ⋯ , p } \mathcal{P}=\left\{x \mid a_j^T x \leqslant b_j, j=1, \cdots, m, c_j^T x=d_j, j=1, \cdots, p\right\} P={x∣ajTx⩽bj,j=1,⋯,m,cjTx=dj,j=1,⋯,p}
其为有限个半空间和超平面的交集,下图为五个半空间组成的一个多面体示意图。
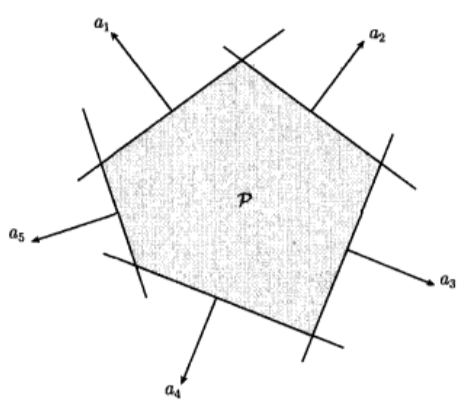
多面体也可以写成如下更为紧凑的形式:
P = { x ∣ A x ⪯ b , C x = d } A = [ a 1 T ⋮ a m T ] , C = [ c 1 T ⋮ c p T ] , \begin{gathered} \mathcal{P}=\{x \mid A x \preceq b, C x=d\} \\ A=\left[\begin{array}{c} a_1^T \\ \vdots \\ a_m^T \end{array}\right], \quad C=\left[\begin{array}{c} c_1^T \\ \vdots \\ c_p^T \end{array}\right], \end{gathered} P={x∣Ax⪯b,Cx=d}A= a1T⋮amT ,C= c1T⋮cpT ,
其中 ⪯ \preceq ⪯表示 R m \mathbf{R}^m Rm上的向量不等式或分量不等式。
半正定锥
**半正定锥:**利用 S n \mathbf{S}^n Sn表示对称 n × n n\times n n×n矩阵的集合, S + n \mathbf{S}^n_+ S+n表示对称半正定矩阵的集合, S + + n \mathbf{S}^n_{++} S++n表示对称正定矩阵的集合,即
S n = { X ∈ R n × n ∣ X = X T } S + n = { X ∈ S n ∣ X ⪰ 0 } S + + n = { X ∈ S n ∣ X ≻ 0 } \begin{aligned} & \mathbf{S}^n=\left\{X \in \mathbf{R}^{n \times n} \mid X=X^T\right\} \\ & \mathbf{S}_{+}^n=\left\{X \in \mathbf{S}^n \mid X \succeq 0\right\} \\ & \mathbf{S}_{++}^n=\left\{X \in \mathbf{S}^n \mid X \succ 0\right\} \end{aligned} Sn={X∈Rn×n∣X=XT}S+n={X∈Sn∣X⪰0}S++n={X∈Sn∣X≻0}
其中集合 S + n \mathbf{S}^n_+ S+n为一个凸锥。
保凸运算
保凸运算可以从已知的凸集构造出其他凸集,能够用来确定和构建具有凸性的集合。
交集
凸集的交集运算是保凸的:如果 S 1 S_1 S1和 S 2 S_2 S2是凸集,那么 S 1 ∩ S 2 S_1\cap S_2 S1∩S2也是凸集,这个性质也能够扩展到无穷多个集合的交。
仿射函数
**仿射函数:**如果一个函数是一个线性函数和一个常数的和,即具有 f ( x ) = A x + b f(x)=Ax+b f(x)=Ax+b的形式,其中 A ∈ R m × n , b ⊆ R m A\in\mathbf{R^{m\times n}},b\subseteq\mathbf{R^m} A∈Rm×n,b⊆Rm。
如果 S ⊆ R n S\subseteq\mathbf{R}^n S⊆Rn是凸的,并且 f : R n → R m f:\mathbf{R^n}\rightarrow\mathbf{R^m} f:Rn→Rm是仿射函数。那么, S S S在 f f f下的象
f ( S ) = { f ( x ) ∣ x ∈ S } f(S)=\{f(x)\mid x\in S\} f(S)={f(x)∣x∈S}
也是凸的。同样类似的,如果 f : R k → R n f:\mathbf{R^k}\rightarrow\mathbf{R^n} f:Rk→Rn是仿射函数,那么 S S S在 f f f下的原象
f − 1 ( S ) = { x ∣ f ( x ) ∈ S } f^{-1}(S)=\{x\mid f(x)\in S\} f−1(S)={x∣f(x)∈S}
也是凸的。
例子
- 伸缩与平移:如果 S ⊆ R n S\subseteq\mathbf{R}^n S⊆Rn, α ∈ R \alpha\in\mathbf{R} α∈R并且 a ∈ R n a\in\mathbf{R^n} a∈Rn,那么,集合 α S \alpha S αS和集合 S + a S + a S+a是凸的。
- 直积:如果 S 1 S_1 S1和 S 2 S_2 S2都是凸集,那么其直积也是凸集,其直积可以表示为
S 1 × S 2 = { ( x 1 , x 2 ) ∣ x 1 ∈ S 1 , x 2 ∈ S 2 } S_{1} \times S_{2}=\left\{\left(x_{1}, x_{2}\right) \mid x_{1} \in S_{1}, x_{2} \in S_{2}\right\} S1×S2={(x1,x2)∣x1∈S1,x2∈S2}
线性分式和透视函数
**透视函数:**定义 P : R n + 1 → R n P:\mathbf{R^{n+1}\rightarrow\mathbf{R^n}} P:Rn+1→Rn, P ( z , t ) = z / t P(z,t)=z/t P(z,t)=z/t为透视函数,其定义域为 dom P = R n × R + + \textbf{dom}P=\mathbf{R^n}\times\mathbf{R_{++}} domP=Rn×R++。其中 R + + \mathbf{R_{++}} R++表示正实数集合。透视函数对向量进行伸缩,或者称为规范化,使得最后一维分量为1并且舍弃掉。
**性质:**如果 C ⊆ dom P C\subseteq\textbf{dom}P C⊆domP是凸集,那么他的象
P ( C ) = { P ( x ) ∣ x ∈ C } P(C)=\{P(x)\mid x \in C \} P(C)={P(x)∣x∈C}
也是凸集。同样一个凸集在透视函数的原象也是凸的。
**线性分式函数:**线性分式函数由透视函数和仿射函数符合而成。设 g : R n → R m + 1 g:\mathbf{R^n}\rightarrow\mathbf{R^{m+1}} g:Rn→Rm+1是仿射的,即
g ( x ) = [ A c T ] x + [ b d ] g(x)=\left[\begin{array}{c} A \\ c^{T} \end{array}\right] x+\left[\begin{array}{l} b \\ d \end{array}\right] \\ g(x)=[AcT]x+[bd]
其中 A ∈ R m × n , b ∈ R m , c ∈ R n A\in\mathbf{R^{m\times n}},b\in\mathbf{R^m},c\in\mathbf{R^n} A∈Rm×n,b∈Rm,c∈Rn并且 d ∈ R d\in\mathbf{R} d∈R。则由$f=P \circ g 给出的函数 给出的函数 给出的函数f:\mathbf{Rn}\rightarrow\mathbf{Rm}$
f ( x ) = ( A x + b ) / ( c T x + d ) , dom f = { x ∣ c T x + d > 0 } \quad f(x)=(A x+b) /\left(c^{T} x+d\right), \quad \operatorname{dom} f=\left\{x \mid c^{T} x+d>0\right\} f(x)=(Ax+b)/(cTx+d),domf={x∣cTx+d>0}
称为线性分式(或者投射)函数。值得注意的是如果 c = 0 , d > 0 c=0,d>0 c=0,d>0,则 f f f的定义域为 R n \mathbf{R}^n Rn,并且 f f f是仿射函数。因此,我饿们可以将仿射和线性函数视为特殊的线性分式函数。
**性质:**类似于透视函数,线性分式函数也是保凸的。如果 C C C是凸集,那么其在线性分式函数下的象和原象都是凸的。
广义不等式
正常锥和广义不等式
**正常锥:**满足以下条件的锥 K ⊆ R n K\subseteq \mathbf{R}^n K⊆Rn为正常锥
- K K K是凸的
- K K K是闭的
- K K K是实的,即具有非空内部
- K K K是尖的,即不包含直线(或者等价地, x ∈ K , − x ∈ K ⇒ x = 0 x\in K,-x\in K\Rightarrow x=0 x∈K,−x∈K⇒x=0)
正常锥常用来定义广义不等式。用正常锥 K K K可以定义 R n \mathbf{R^n} Rn上的偏序关系如下
x ⪯ K y ⟺ y − x ∈ K x\preceq_Ky\Longleftrightarrow y-x\in K x⪯Ky⟺y−x∈K
同样,可以定义相应的严格偏序关系
x ≺ K y ⟺ y − x ∈ int K x\prec_Ky\Longleftrightarrow y-x\in \textbf{int}K x≺Ky⟺y−x∈intK
广义不等式 ⪯ \preceq ⪯的性质
- ⪯ K \preceq_K ⪯K对于加法是保序的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 u ⪯ K v u\preceq_Kv u⪯Kv,那么 x + u ⪯ K y + v x+u\preceq_Ky+v x+u⪯Ky+v。
- ⪯ K \preceq_K ⪯K具有传递性:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 y ⪯ K z y\preceq_Kz y⪯Kz,那么 x ⪯ K z x\preceq_Kz x⪯Kz。
- ⪯ K \preceq_K ⪯K对于非负数乘是保序的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 α ≥ 0 \alpha\ge 0 α≥0,那么 α x ⪯ K α y \alpha x\preceq_K\alpha y αx⪯Kαy。
- ⪯ K \preceq_K ⪯K是自反的: x ⪯ K x x\preceq_Kx x⪯Kx。
- ⪯ K \preceq_K ⪯K是反对称的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 y ⪯ K x y\preceq_Kx y⪯Kx,那么 x = y x=y x=y。
- ⪯ K \preceq_K ⪯K对于极限运算是保序的:如果对于 i = 1 , 2 , ⋯ i=1,2,\cdots i=1,2,⋯均有 x i ⪯ K y i x_i\preceq_Ky_i xi⪯Kyi,当 i → ∞ i\rightarrow\infty i→∞时,由 x i → x x_i\rightarrow x xi→x和 y i → y y_i\rightarrow y yi→y,那么 x ⪯ K y x\preceq_Ky x⪯Ky。
最小和极小元
**最小元:**对于每个 y ∈ S y\in S y∈S,均有 x ⪯ K y x\preceq_Ky x⪯Ky ,则称 x ∈ S ,则称x\in S ,则称x∈S是 S S S(关于广义不等式 ⪯ K \preceq_K ⪯K)的最小元。
**最大元:**对于每个 y ∈ S y\in S y∈S,均有 x ⪰ K y x\succeq_Ky x⪰Ky ,则称 x ∈ S ,则称x\in S ,则称x∈S是 S S S(关于广义不等式 ⪯ K \preceq_K ⪯K)的最大元。
**极小元:**如果 y ∈ S , y ⪯ K x y\in S,y\preceq_Kx y∈S,y⪯Kx可以推得 y = x y=x y=x,那么我们称 x ∈ S x\in S x∈S是 S S S上(关于广义不等式 ⪯ K \preceq_K ⪯K)的极小元。
极大元:如果 y ∈ S , y ⪰ K x y\in S,y\succeq_Kx y∈S,y⪰Kx可以推得 y = x y=x y=x,那么我们称 x ∈ S x\in S x∈S是 S S S上(关于广义不等式 ⪯ K \preceq_K ⪯K)的极大元。
分离与支撑超平面
**超平面分离定理:**假设 C C C和 D D D是两个不相交的凸集,即 C ∩ D = ⊘ C\cap D=\oslash C∩D=⊘,那么存在 a ≠ 0 a\neq 0 a=0和 b b b使得超平面 { x ∣ a T x = b } \{x\mid a^Tx=b\} {x∣aTx=b}能够将两个凸集分离。如下图所示。

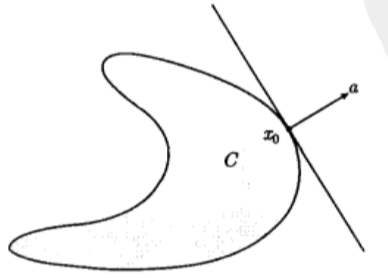
**支撑超平面:**设 C ⊆ R n C\subseteq\mathbf{R}^n C⊆Rn而 x 0 x_0 x0为其边界一点,如果 a ≠ 0 a\neq0 a=0,并且对于任意 x ∈ C x\in C x∈C满足 a T x ≤ a T x 0 a^Tx\le a^Tx_0 aTx≤aTx0,那么称超平面 { x ∣ a T x = a T x 0 } \{x\mid a^Tx= a^Tx_0\} {x∣aTx=aTx0} 为集合 C C C在点 x 0 x_0 x0处的支撑超平面。在几何上表示为超平面 { x ∣ a T x = a T x 0 } \{x\mid a^Tx= a^Tx_0\} {x∣aTx=aTx0}与 C C C相切于点 x 0 x_0 x0,如下图所示:
对偶锥和广义不等式
对偶锥: K K K为一个锥,集合
$$
$$
称为 K K K的对偶锥。 K ∗ K^* K∗总是一个凸锥,即使 K K K不是凸锥。从几何上看, y ∈ K ∗ y\in K^* y∈K∗当且仅当 − y -y −y是 K K K在原点的一个支撑超平面的法线,如下图所示:
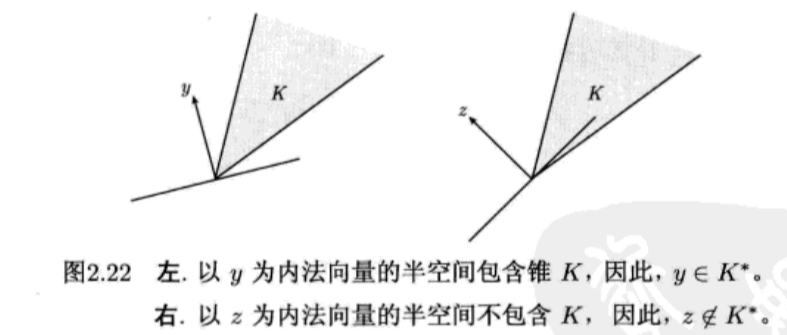
性质
-
K ∗ K^* K∗是闭凸锥。
-
K 1 ⊆ K 2 K_1\subseteq K_2 K1⊆K2可以导出 K 2 ∗ ⊆ K 1 ∗ K_{2}^*\subseteq K_1^* K2∗⊆K1∗。
-
如果 K K K由非空内部,那么 K ∗ K^* K∗是尖的(不含直线)。
-
如果 K K K的闭包是尖的,那么 K ∗ K^* K∗有非空内部。
-
K ∗ ∗ K^{**} K∗∗是 K K K的凸包的闭包。(因此,如果 K K K是凸和闭得,则 K ∗ ∗ = K K^{**}=K K∗∗=K)。
-
如果 K K K是一个正常锥,那么它的对偶 K ∗ K^{*} K∗也是,进一步将, K ∗ ∗ = K K^{**}=K K∗∗=K。
不是凸锥。从几何上看, y ∈ K ∗ y\in K^* y∈K∗当且仅当 − y -y −y是 K K K在原点的一个支撑超平面的法线,如下图所示:
[外链图片转存中…(img-iMHjGdPV-1692066222841)]
性质
-
K ∗ K^* K∗是闭凸锥。
-
K 1 ⊆ K 2 K_1\subseteq K_2 K1⊆K2可以导出 K 2 ∗ ⊆ K 1 ∗ K_{2}^*\subseteq K_1^* K2∗⊆K1∗。
-
如果 K K K由非空内部,那么 K ∗ K^* K∗是尖的(不含直线)。
-
如果 K K K的闭包是尖的,那么 K ∗ K^* K∗有非空内部。
-
K ∗ ∗ K^{**} K∗∗是 K K K的凸包的闭包。(因此,如果 K K K是凸和闭得,则 K ∗ ∗ = K K^{**}=K K∗∗=K)。
-
如果 K K K是一个正常锥,那么它的对偶 K ∗ K^{*} K∗也是,进一步将, K ∗ ∗ = K K^{**}=K K∗∗=K。
相关文章:

凸优化基础学习——凸集
凸优化基础学习——凸集 文章内容全部来自对Stephen Boyd and Lieven vandenberghe的Convex Optimization的总结归纳。 电子书资源: 链接:https://pan.baidu.com/s/1dP5zI6h3BEyGRzSaJHSodg?pwd0000 提取码:0000 基本概念 仿射集合 **…...

oracle 19c环境常见问题汇总
1、rman备份时会消耗这么多临时表空间 参考MOS: RMAN-08132: Warning: Cannot Update Recovery Area ORA-01652: unable to extend temp segment by 64 in tablespace TEMP (Doc ID 2658437.1) Known RMAN Performance Problems (Doc ID 247611.1) 处理办法&…...

django实现悲观锁乐观锁
前期准备 # 线上卖图书-图书表 图书名字,图书价格,库存字段-订单表: 订单id,订单名字# 表准备class Book(models.Model):name models.CharField(max_length32)price models.IntegerField() #count models.SmallIntegerField…...
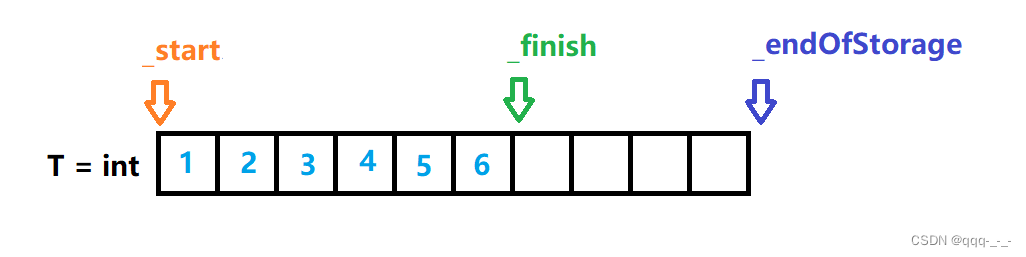
vector【2】模拟实现(超详解哦)
vector 引言(实现概述)接口实现详解默认成员函数构造函数析构函数赋值重载 迭代器容量size与capacityreserveresizeempty 元素访问数据修改inserterasepush_back与pop_backswap 模拟实现源码概览总结 引言(实现概述) 在前面&…...

金融助贷公司怎么获客——大数据获客
2023年已过去大半,整个贷款领域遭遇的现象仍然是拓客难、拓客贵、顾客精确度不高难题。从业者工作压力与日俱增,每日遭遇各种各样考评,因此大家并不是在开发客户便是在开发客户的路上。贷款市场销售艰难变成一个问题,很多贷款营销…...
Java进阶-Oracle(二十一)(2)
🌻🌻 目录 一、Oracle 数据库的操作(DDL DML DQL DCL TPL)1.1 标识符、关键字、函数等1.1.1 数值类型:1.1.2 字符串类型:1.1.3 日期类型1.1.4 大的数据类型--适合保存更多的数据 1.2 运算符1.3 函数---预定义函数、自定义函数&…...

SpringCloud实用篇4——MQ RabbitMQ SpringAMQP
目录 1 初识MQ1.1 同步和异步通讯1.1.1 同步通讯1.1.2 异步通讯 1.2 技术对比 2.快速入门2.1 安装RabbitMQ2.1.1 单机部署2.1.2集群部署 2.2 RabbitMQ消息模型2.3.导入Demo工程2.4 入门案例2.4.1 publisher实现2.4.2 consumer实现 3 SpringAMQP3.1 Basic Queue 简单队列模型3.1…...
【BASH】回顾与知识点梳理(二十二)
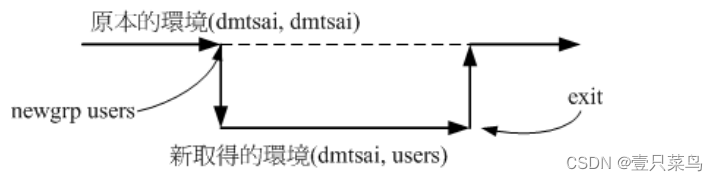
【BASH】回顾与知识点梳理 二十二 二十二. Linux 账号管理22.1 Linux 的账号与群组使用者标识符: UID 与 GID使用者账号/etc/passwd 文件结构/etc/shadow 文件结构 关于群组: 有效与初始群组、groups, newgrp/etc/group 文件结构有效群组(effective grou…...
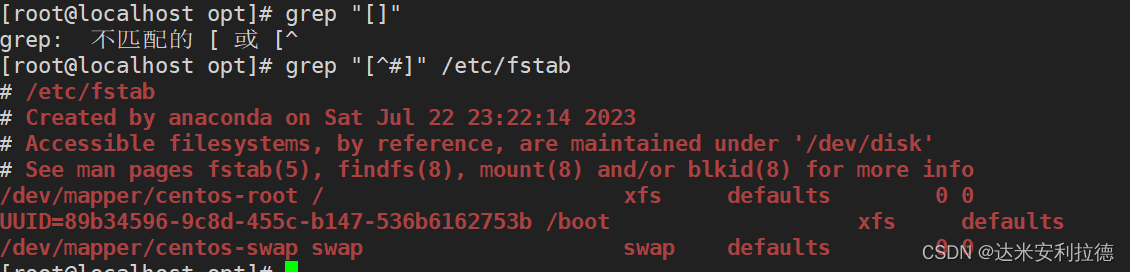
shell脚本之正则表达式
目录 一.常见的管道命令1.1sort命令1.2uniq命令1.3tr命令1.4cut命令1.5实例1.5.1统计当前主机连接状态1.5.2统计当前主机数 二.正则表达式2.1正则表达式的定义2.2常见元字符(支持的工具:find,grep,egrep,sed和awk&…...
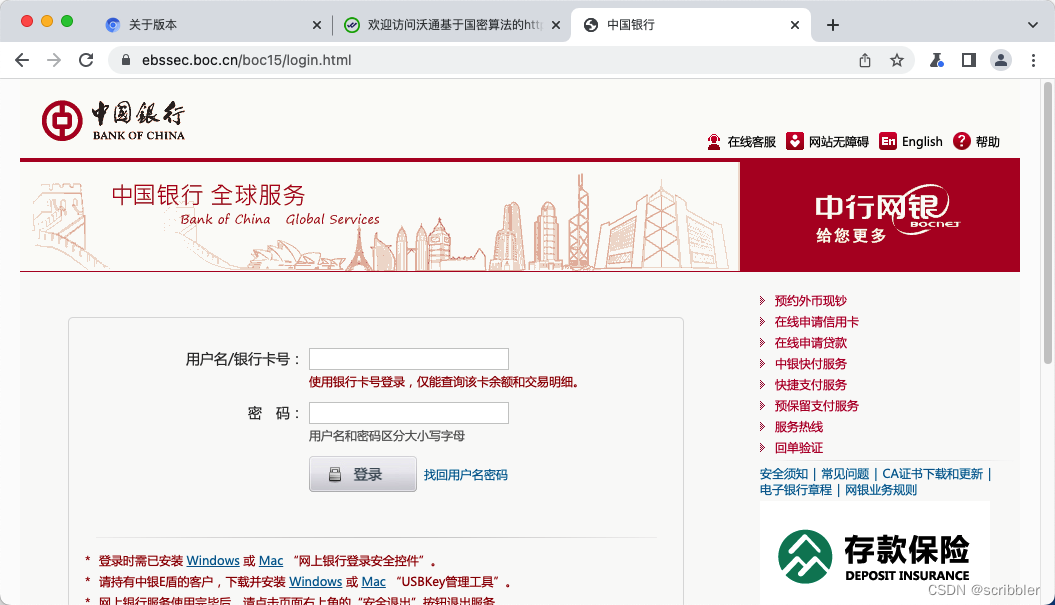
将SM2根证书预置到chromium中
最近花了很多精力在做chromium的GmSSL适配,协议和算法都已经完成,这篇文章是关于将SM2根证书预置到chromium中 我的开发测试环境是macos12.4,从chromium的代码和文档中得知证书获取和校验都是通过操作系统以及native api接口完成,…...
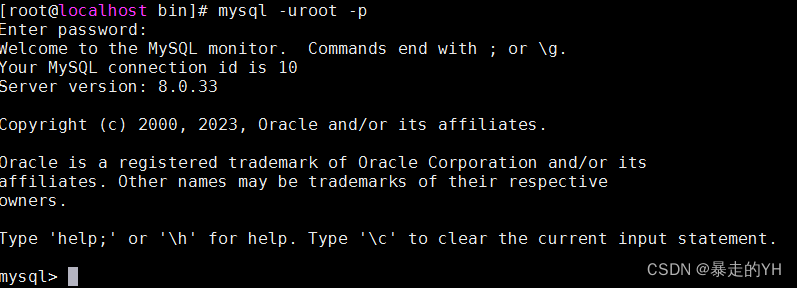
linux安装mysql-8.0.33正确方式及常见问题
目录 获取mysql下载地址链接 解压安装包 复制文件到安装目录 添加用户和用户属组修改权限 创建存储数据的文件夹/usr/local/mysql 初始化安装 修改配置文件 创建日志文件并赋予对应权限 启动成功编辑 创建软链接 之前安装过mysql,时间比较长忘记安装步骤了今天…...
Vim的插件管理器之Vundle
1、安装Vundle插件管理器 Vim可以安装插件,但是需要手动安装比较麻烦,Vim本身没有提供插件管理器,所以会有很多的第三方的插件管理器,有一个vim的插件叫做 “vim-easymotion”,在它的github的安装说明里有列出对于不同…...
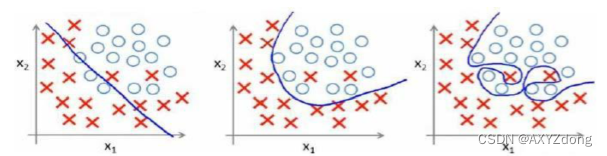
机器学习丨1. 机器学习概述
Author:AXYZdong 硕士在读 工科男 有一点思考,有一点想法,有一点理性! 定个小小目标,努力成为习惯!在最美的年华遇见更好的自己! CSDNAXYZdong,CSDN首发,AXYZdong原创 唯…...
清除pip安装库时的缓存
目录 1、命令清除缓存 2、路径手动清除 在使用pip安装Python库时,如果之前已经下载过该库,pip会默认使用缓存来安装库,而不是重新从网络上下载。缓存文件通常存储在用户目录下的缓存文件夹中,具体位置因操作系统和Python版本而异…...
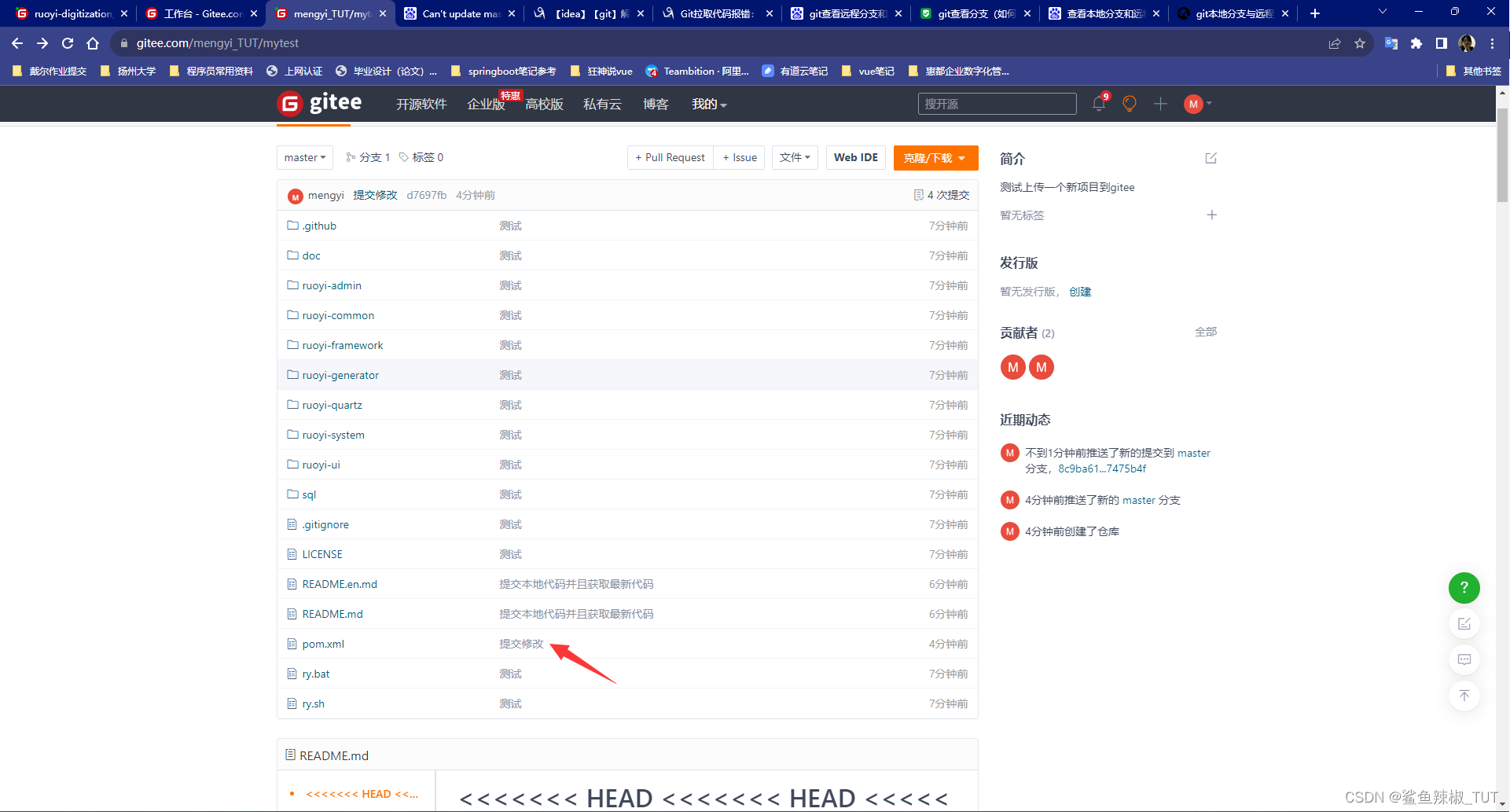
gitee上传一个本地项目到一个空仓库
gitee上传一个本地项目到一个空仓库 引入 比如,你现在本地下载了一个半成品的框架,现在想要把这个本地项目放到gitee的仓库上,这时就需要我们来做到把这个本地项目上传到gitee上了。 具体步骤 1. 登录码云 地址:https://gite…...

力扣:63. 不同路径 II(Python3)
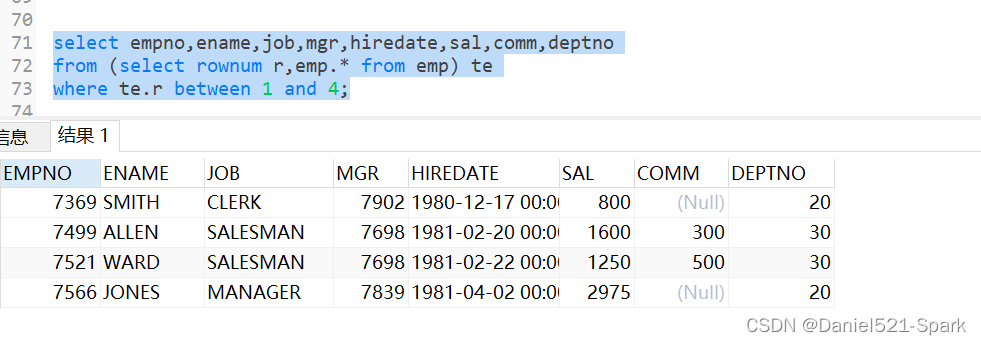
题目: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从…...

【C语言】每日一题(多数元素)
多数元素,链接奉上 方法 1.摩尔投票2.合理但错误的方法2.1暴力循环2.2排序求出中间元素中间元素 1.摩尔投票 先来简单的介绍摩尔投票: 摩尔投票是一种用来解决绝对众数问题的算法。 什么是绝对众数呢? 在一个集合中,如果一个元素…...
)
后端 .net7 Minimal API 限流中间件(微信小程序无师自通十)
我的微信小程序使用.net7 Minimal API 作为后端,当服务器摆上公网后,可以观察到很多的攻击行为和暴力访问。所以,我需要使用微软的限流中间件部署相应的功能在服务器上 关键字: AddFixedWindowLimiter using Microsoft.AspNetCo…...

背上沉重的书包准备面试之react篇
目录 react特性? react生命周期? state和props区别 react中setState执行机制? 在react类组件形式中,setState第二个参数的作用? react事件机制? react事件绑定方式有哪些? react组件之间…...
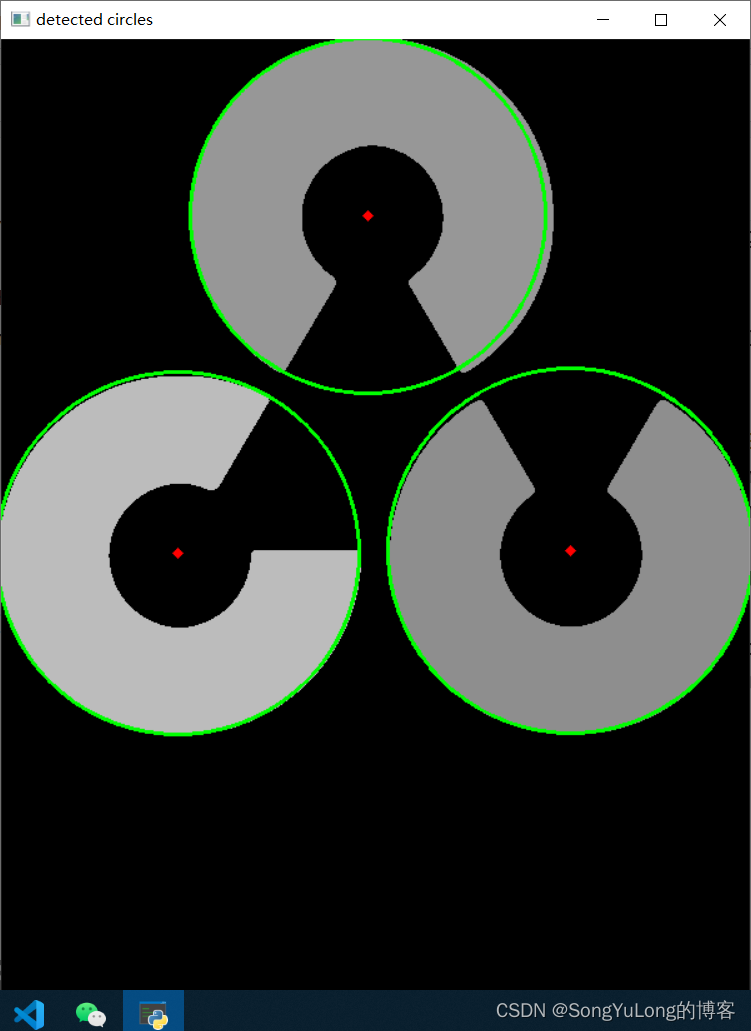
OpenCV-Python中的图像处理-霍夫变换
OpenCV-Python中的图像处理-霍夫变换 霍夫变换霍夫直线变换霍夫圆环变换 霍夫变换 霍夫(Hough)变换在检测各种形状的技术中非常流行,如果要检测的形状可以用数学表达式描述,就可以是使用霍夫变换检测它。即使要检测的形状存在一点破坏或者扭曲也是可以使…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
