微服务部署中的动态扩缩容和故障迁移实践经验!快来看看!
随着微服务架构的快速普及,越来越多的组织开始将传统的单体应用转变为分布式的微服务系统。在这种架构下,动态扩缩容和故障迁移变得尤为重要,因为它们能够帮助我们应对不断变化的负载和故障情况。本文将详细介绍动态扩缩容和故障迁移的概念,并探讨了一些实际的解决方案。

1. 动态扩缩容
1.1 概念和原理
在微服务架构中,动态扩缩容是指根据当前负载情况自动调整系统的资源,以应对不断变化的需求。这可以通过水平扩展和垂直扩展实现。水平扩展是指增加实例数量,垂直扩展是指增加资源配额。
1.2 解决方案和实践
在实践中,动态扩缩容可以使用自动化工具来实现,如容器编排工具Kubernetes和Docker Swarm等。这些工具提供了自动伸缩功能,可以根据预先设定的规则自动添加或移除实例。
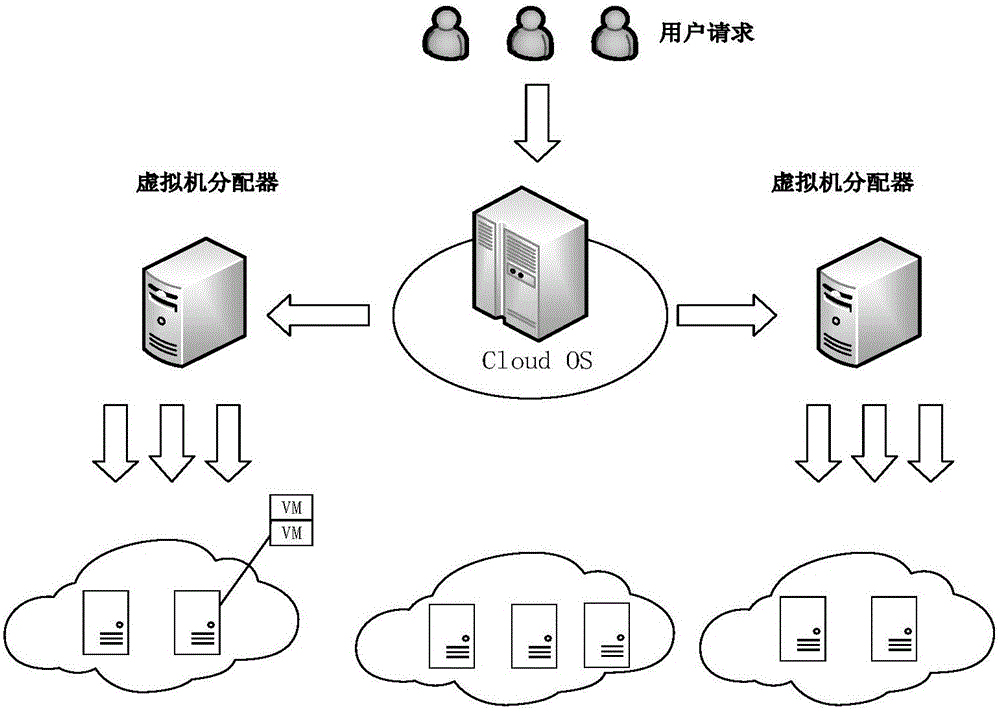
2. 故障迁移
2.1 概念和原理
在微服务系统中,故障是不可避免的,因此,故障迁移是必不可少的。故障迁移是指将故障实例从一个节点迁移到另一个正常节点的过程,以确保系统的可用性和可靠性。
2.2 解决方案和实践
常见的故障迁移解决方案包括负载均衡器和容器编排工具。负载均衡器可以根据实例的可用性和负载情况自动将请求分发到可用的实例。容器编排工具可以监测实例状态,并在检测到故障时迅速迁移。
3. 实施最佳实践
3.1 设定合理的自动化策略
在实施动态扩缩容和故障迁移时,需要设定合理的自动化策略,以平衡系统的可用性和成本效益。例如,设定合理的负载阈值和故障检测机制,避免频繁的扩缩容和迁移。
3.2 监控和日志记录
及时监控系统的负载和性能,对异常进行报警和记录。这有助于发现潜在的故障和性能问题,并及时采取措施。
3.3 迭代和优化
动态扩缩容和故障迁移是一个持续的过程,需要不断迭代和优化。及时收集用户反馈和系统指标,对系统进行调整和改进。
结论:
在微服务部署中,动态扩缩容和故障迁移是确保系统可靠性和弹性的关键策略。本文讨论了动态扩缩容和故障迁移的概念、解决方案和最佳实践。通过合理的策略和工具的选择,可以帮助我们应对不断变化的负载和故障情况,提高系统的可用性和可靠性。
了解更多数据仓库与数据集成关干货内容请关注>>>
数据集成技术分享集锦
免费试用、获取更多信息,点击了解更多>>>
FineDataLink-帆软FDL|一站式数据集成平台|数据同步|数据清洗|API接口数据发布|告别T+1
FineDataLink是一款低代码/高效率的ETL工具,同时也是一款数据集成工具,它可以帮助企业快速构建数据仓库,对数据进行管理、分析和使用,提高数据治理效率和质量。FineDataLink在进行iPaaS领域的尝试,结合流批一体引擎、流程调度引擎,打造具有帆软特点的集成平台,通过全新的插件引擎,能够极大程度让用户自定义各类数据源的同步、计算、流程控制和调度策略。
相关文章:

微服务部署中的动态扩缩容和故障迁移实践经验!快来看看!
随着微服务架构的快速普及,越来越多的组织开始将传统的单体应用转变为分布式的微服务系统。在这种架构下,动态扩缩容和故障迁移变得尤为重要,因为它们能够帮助我们应对不断变化的负载和故障情况。本文将详细介绍动态扩缩容和故障迁移的概念&a…...

代码随想录第四十五天
代码随想录第四十五天 Leetcode 70. 爬楼梯Leetcode 322. 零钱兑换Leetcode 279. 完全平方数 Leetcode 70. 爬楼梯 题目链接: 爬楼梯 自己的思路:之前是用斐波那契做的,但是现在学了完全背包,可以将m2拓展的更大一点,我们可以将楼顶n设为背包…...
Vue Baidu Map--自定义点图标bm-marker
自定义点图标 将准备好的图标放到项目中 使用import引入, 并在data中进行声明 <script> import mapIconRed from ./vue-baidu-map/img/marker_red_sprite.png export default {data() {return {mapIconRed,}}, } </script>在<bm-marker>中加入参…...

ZooKeeper的基本概念
集群角色 通常在分布式系统中,构成一个集群的每一台机器都有自己的角色,最典型的集群模式就是Master/Slave模式(主备模式)。在这种模式中,我们把能够处理所有写操作的机器称为Master机器,把所有通过异步复制方式获取最新数据&…...
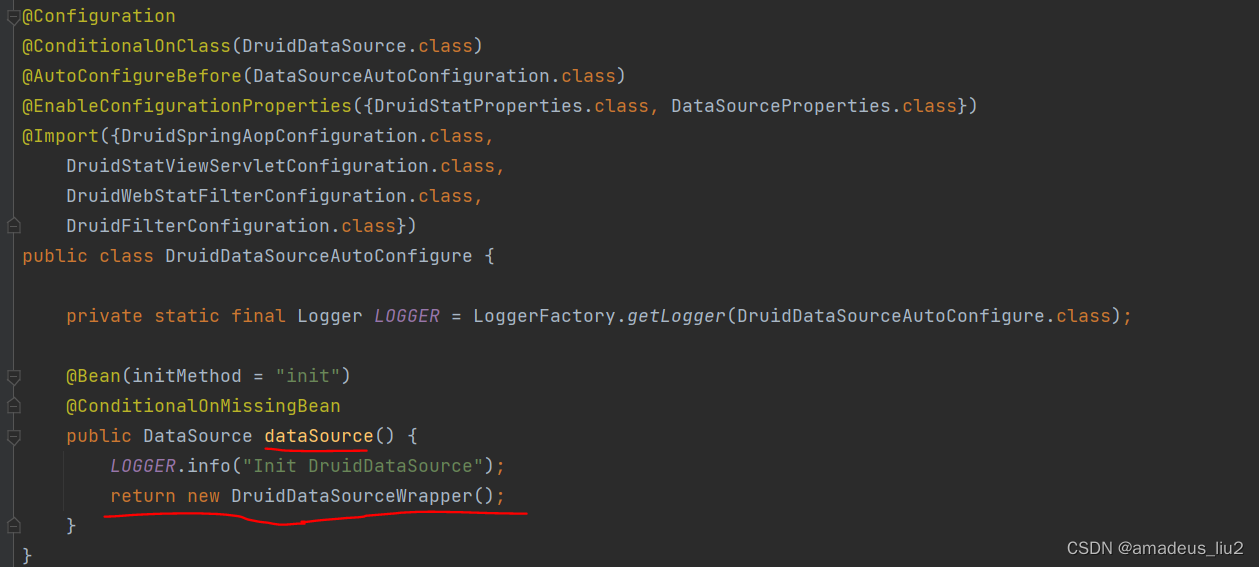
SpringBoot复习:(51)默认情况下DataSource是怎么创建出来的,是什么类型的?
DataSource是通过DataSourceAutoConfiguration创建的,这个类代码如下: 可以看到DataSourceAutoConfiguration有个静态内部类PooledDataSourceConfiguration,在这个类上有个Import注解,导入了DataSourceConfiguration.Hikari这个类࿰…...
Python+Selenium自动化测试环境搭建步骤(selenium环境搭建)
一、自动化简介 1.自动化测试概念: 是把以人为驱动的测试转化为机器执行的一种过程,它是一种以程序测试程序的过程 2.自动化测试分类: 一般IT上所说的自动化测试是指功能自动化测试,通过编码的方式用一段程序来测试一个软件的功…...

实现简单纯Canvas文本输入框,新手适用
文章目录 概要效果技术细节代码 概要 Canvas上面提供输入: 一、最简单可能是用dom渲染一个input,覆盖在图形上面进行文本编辑,编辑完再把内容更新到图形.这样简单,但是缺点也明显,就是它不是真正绘制在canvas上面,没…...
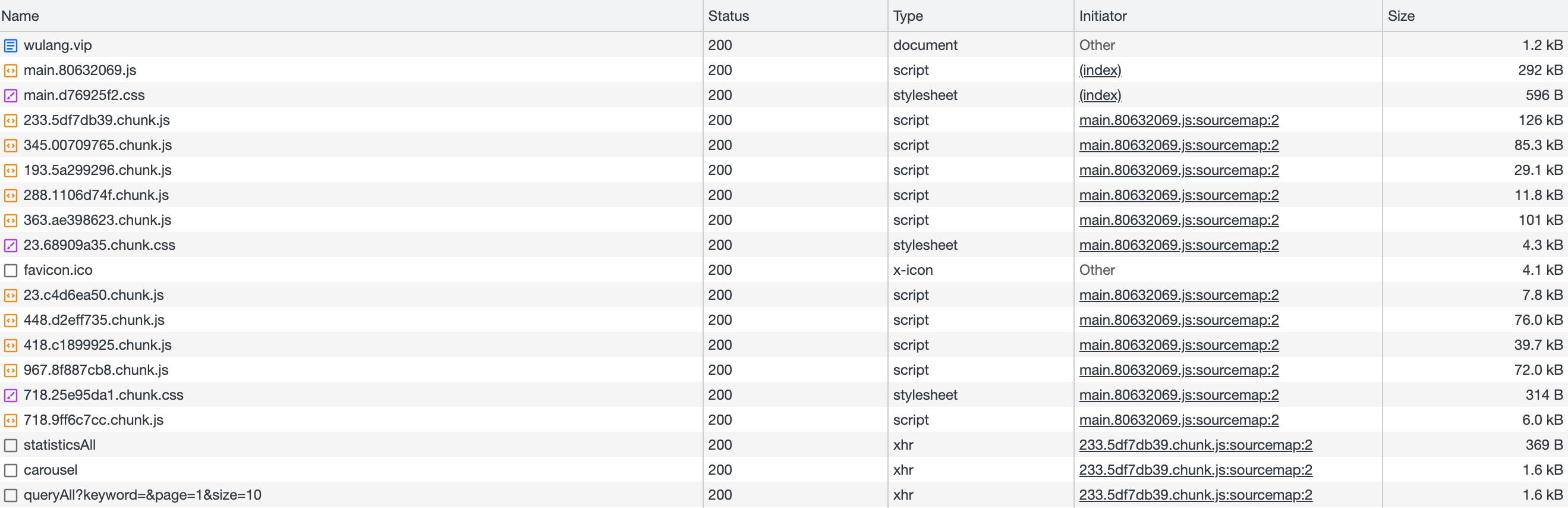
React构建的JS优化思路
背景 之前个人博客搭建时,发现页面加载要5s才能完成并显示 问题 React生成的JS有1.4M,对于个人博客服务器的带宽来说,压力较大,因此耗费了5S的时间 优化思路 解决React生成的JS大小,因为我用的是react-router-dom…...

vim键盘图
国外:http://www.viemu.com/a_vi_vim_graphical_cheat_sheet_tutorial.html,原创,有SVG图,有分步骤的图。 国内翻译:[https://blog.csdn.net/qq_41052753/article/details/101031847 有几个配色,很高清&…...
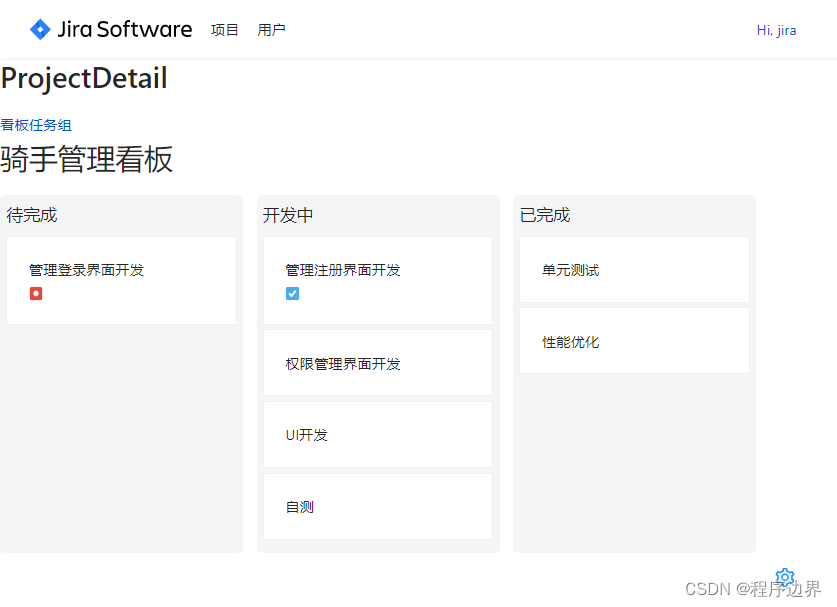
【实战】十一、看板页面及任务组页面开发(一) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(二十三)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...
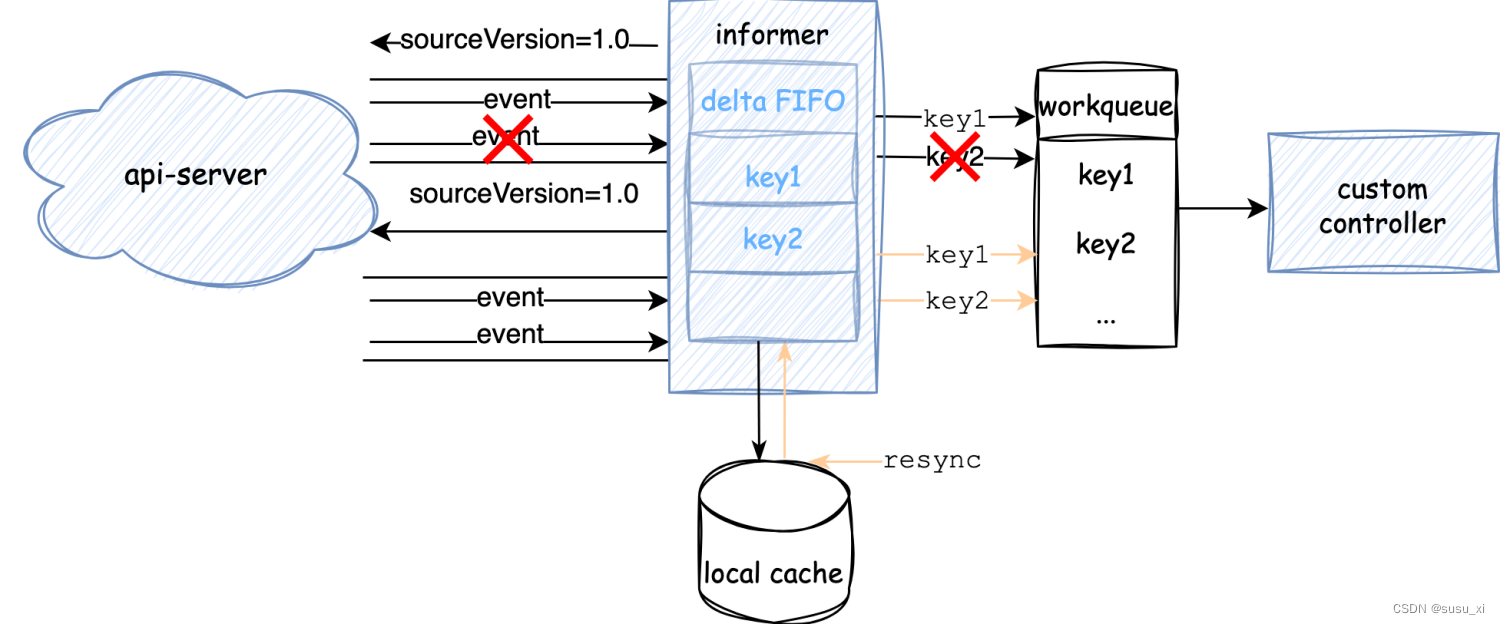
深入源码分析kubernetes informer机制(三)Resync
[阅读指南] 这是该系列第三篇 基于kubernetes 1.27 stage版本 为了方便阅读,后续所有代码均省略了错误处理及与关注逻辑无关的部分。 文章目录 为什么需要resyncresync做了什么 为什么需要resync 如果看过上一篇,大概能了解,client数据主要通…...
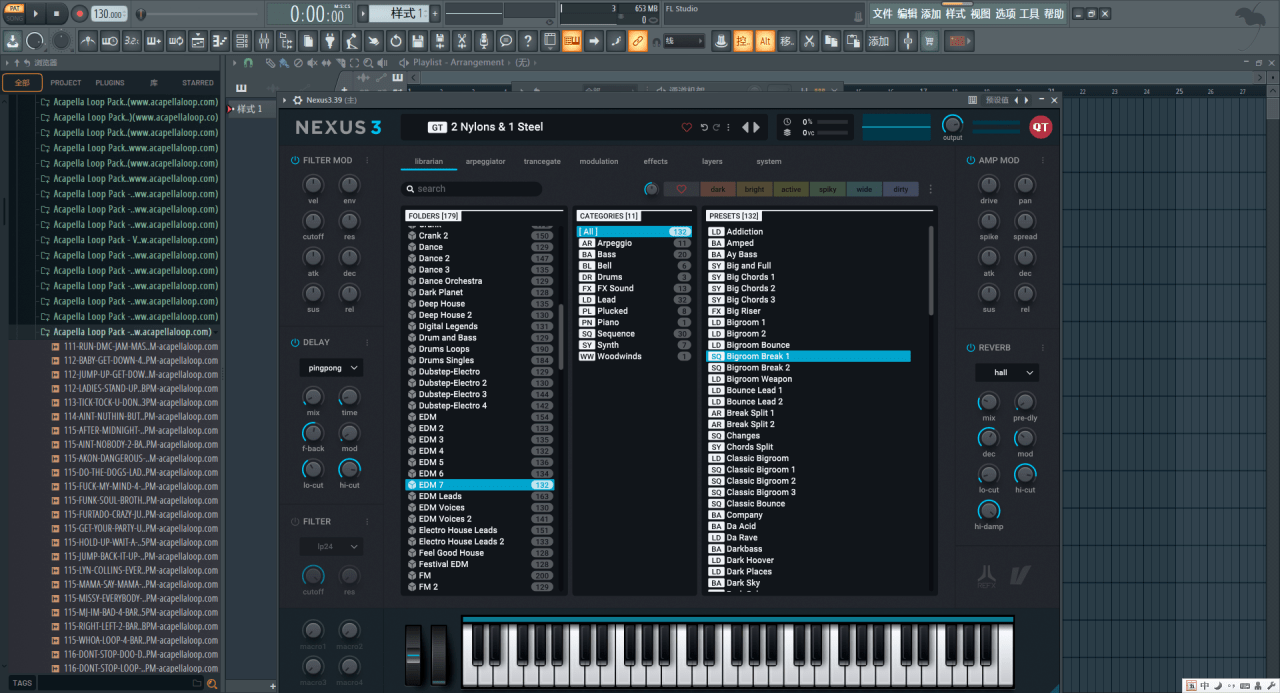
FL Studio 21最新for Windows-21.1.0.3267中文解锁版安装激活教程及更新日志
FL Studio 21最新版本for Windows 21.1.0.3267中文解锁版是最新强大的音乐制作工具。它可以与所有类型的音乐一起创作出令人惊叹的音乐。它提供了一个非常简单且用户友好的集成开发环境(IDE)来工作。这个完整的音乐工作站是由比利时公司 Image-Line 开发…...

HTML详解连载(4)
HTML详解连载(4) 专栏链接 [link](http://t.csdn.cn/xF0H3)下面进行专栏介绍 开始喽CSS定义书写位置示例注意 CSS引入方式内部样式表:学习使用 外部演示表:开发使用代码示例行内样式代码示例 选择器作用基础选择器标签选择器举例特…...

STM32 LL库+STM32CubeMX--点亮板载LED
一、前期准备 硬件:STM32F103C8T6开发板调试工具:DAPLink(本次使用)或USB-TTL开发环境:STM32CubeMX、Keil、Vscode(可选)板载LED:PC13(低电平点亮) 二、STM32CubeMX配置 1.选择芯片型号: 2.配置外设时钟:…...

【HBZ分享】ES的评分score机制的原理
score类型 基础评分boost,默认2.2,逆向文档频率值(IDF):表示该词再文档中(ES中)出现的次数越多,表示越不重要,评分越低关键词在文档中出现的频率(TF):表示该词在文档中出现的频率,频率越高表示…...
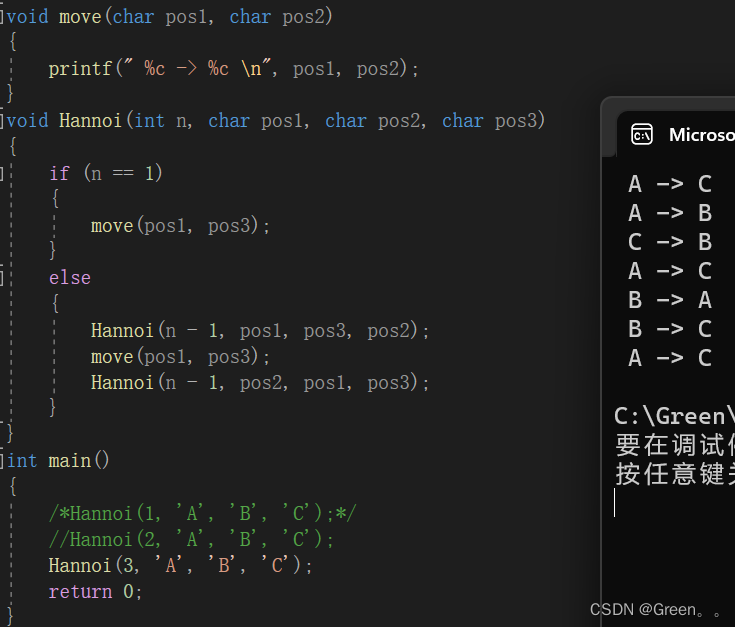
函数递归专题(案例超详解一篇讲通透)
函数递归 前言1.递归案例:案例一:取球问题案例二:求斐波那契额数列案例三:函数实现n的k次方案例四:输入一个非负整数,返回组成它的数字之和案例五:元素逆置案例六:实现strlen案例七:…...

leetcode-413. 等差数列划分(java)
等差数列划分 leetcode-413. 等差数列划分题目描述双指针 上期经典算法 leetcode-413. 等差数列划分 难度 - 中等 原题链接 - 等差数列划分 题目描述 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如࿰…...
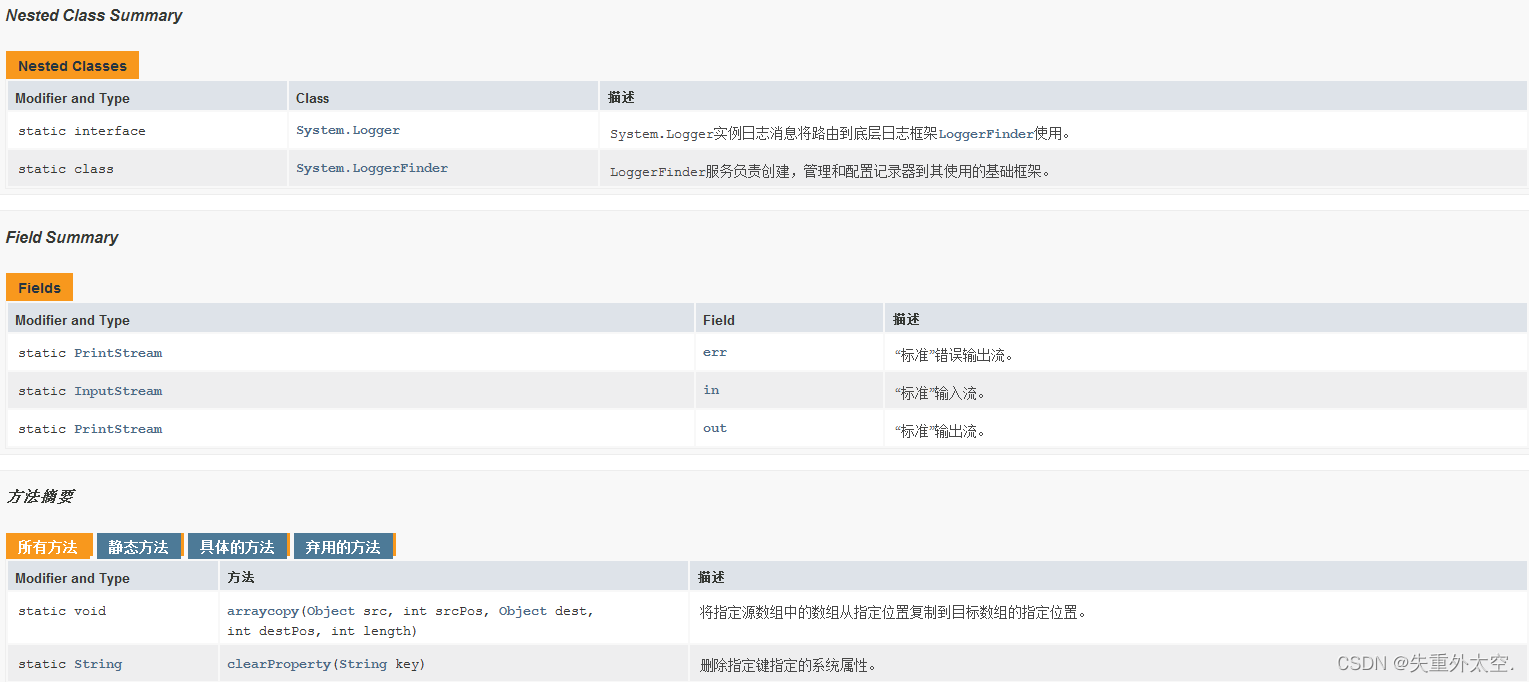
从零开始学习 Java:简单易懂的入门指南之MAth、System(十二)
常见API,MAth、System 1 Math类1.1 概述1.2 常见方法1.3 算法小题(质数)1.4 算法小题(自幂数) 2 System类2.1 概述2.2 常见方法 1 Math类 1.1 概述 tips:了解内容 查看API文档,我们可以看到API文档中关于Math类的定义如下: Math类…...
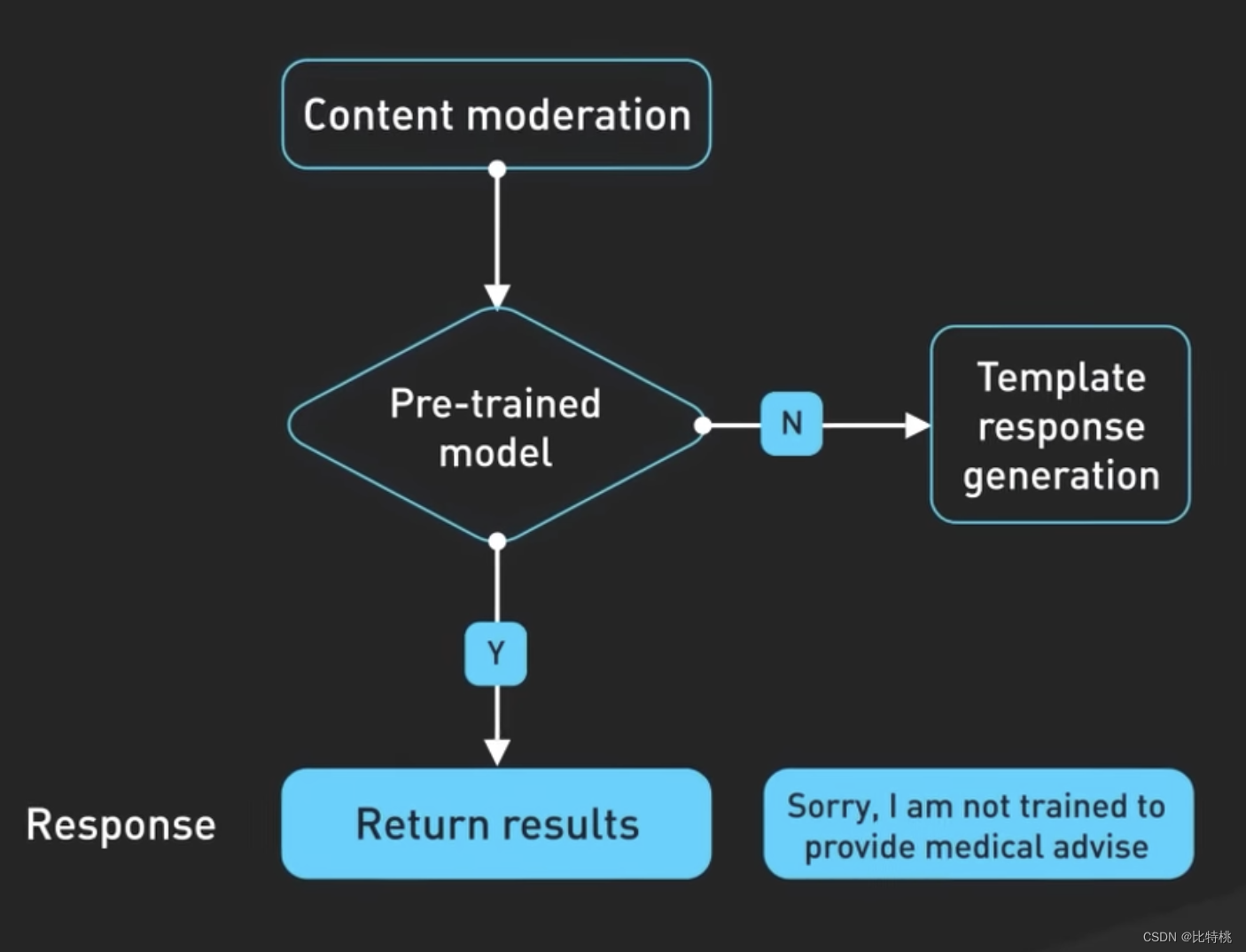
人工智能原理概述 - ChatGPT 背后的故事
大家好,我是比特桃。如果说 2023 年最火的事情是什么,毫无疑问就是由 ChatGPT 所引领的AI浪潮。今年无论是平日的各种媒体、工作中接触到的项目还是生活中大家讨论的热点,都离不开AI。其实对于互联网行业来说,自从深度学习出来后就…...
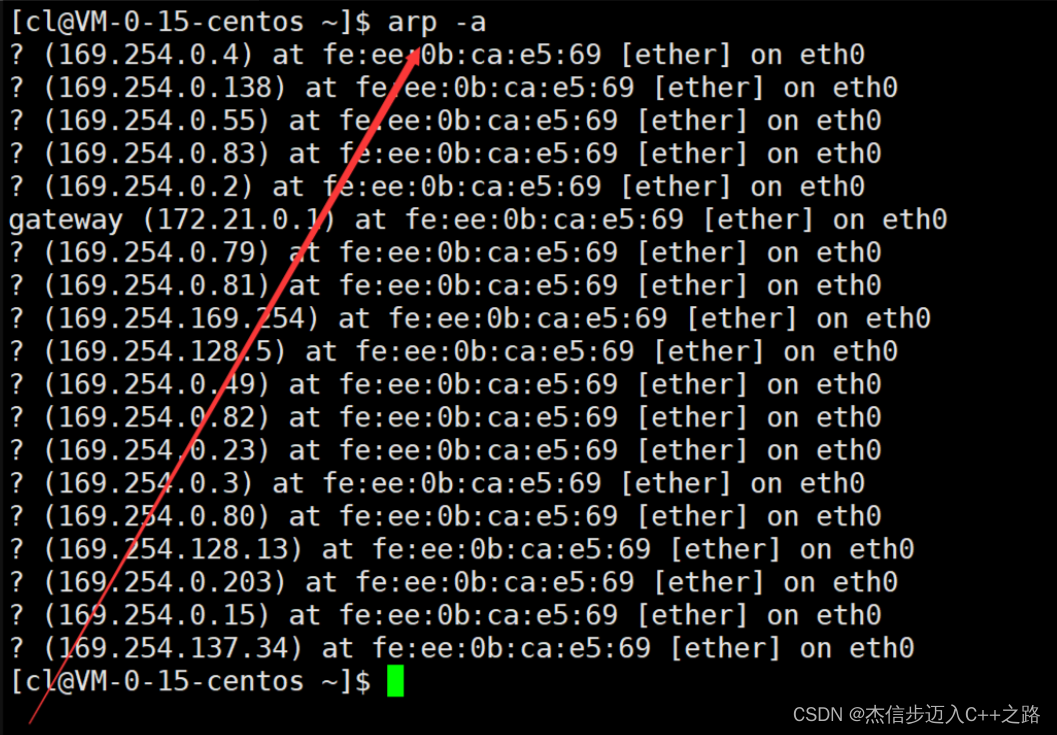
【Linux】以太网协议——数据链路层
链路层解决的问题 IP拥有将数据跨网络从一台主机送到另一台主机的能力,但IP并不能保证每次都能够将数据可靠的送到对端主机,因此IP需要上层TCP为其提供可靠性保证,比如数据丢包后TCP可以让IP重新发送数据,最终在TCP提供的可靠性机…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
