神经网络基础-神经网络补充概念-33-偏差与方差
概念
偏差(Bias):
偏差是模型预测值与实际值之间的差距,它反映了模型对训练数据的拟合能力。高偏差意味着模型无法很好地拟合训练数据,通常会导致欠拟合。欠拟合是指模型过于简单,不能捕捉数据中的复杂模式,导致在训练集和测试集上都表现不佳。
方差(Variance):
方差是模型在不同训练数据集上预测值的变化程度,它反映了模型对训练数据的敏感性。高方差意味着模型过于复杂,对训练数据的小变化非常敏感,通常会导致过拟合。过拟合是指模型在训练集上表现很好,但在未见过的测试数据上表现不佳。
权衡
偏差-方差权衡(Bias-Variance Trade-off):
在实际机器学习中,我们通常希望找到适当的模型复杂度,以平衡偏差和方差之间的关系,从而实现良好的泛化能力。一个理想的模型应该具有适当的复杂度,能够在训练数据上进行合适的拟合,同时又不会过于敏感,可以较好地适应未见过的数据。
解决方法
解决偏差和方差的方法包括:
减小偏差:增加模型的复杂度,使用更多的特征或更深的网络等,以提高模型的表达能力。
减小方差:使用正则化方法,如L1/L2正则化、Dropout等,以减少模型对训练数据的过度拟合。
总结:
偏差反映了模型对训练数据的拟合能力,高偏差通常导致欠拟合。
方差反映了模型对不同训练数据的变化敏感性,高方差通常导致过拟合。
偏差和方差之间存在权衡关系,需要找到适当的模型复杂度来实现良好的泛化能力。
代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error# 生成随机数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + np.random.randn(100, 1) * 0.2# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 创建多项式特征
poly = PolynomialFeatures(degree=10)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)# 使用不同复杂度的模型进行拟合
model_underfit = LinearRegression()
model_properfit = LinearRegression()
model_overfit = LinearRegression()model_underfit.fit(X_train, y_train)
model_properfit.fit(X_train_poly, y_train)
model_overfit.fit(X_train_poly, y_train)# 绘制拟合结果
plt.figure(figsize=(12, 6))plt.subplot(1, 3, 1)
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.plot(X_train, model_underfit.predict(X_train), color='red', label='Underfitting')
plt.legend()
plt.title('Underfitting')plt.subplot(1, 3, 2)
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.plot(X_train, model_properfit.predict(X_train_poly), color='red', label='Properfitting')
plt.legend()
plt.title('Properfitting')plt.subplot(1, 3, 3)
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.plot(X_train, model_overfit.predict(X_train_poly), color='red', label='Overfitting')
plt.legend()
plt.title('Overfitting')plt.tight_layout()
plt.show()# 计算测试集上的均方误差
y_pred_underfit = model_underfit.predict(X_test)
y_pred_properfit = model_properfit.predict(X_test_poly)
y_pred_overfit = model_overfit.predict(X_test_poly)mse_underfit = mean_squared_error(y_test, y_pred_underfit)
mse_properfit = mean_squared_error(y_test, y_pred_properfit)
mse_overfit = mean_squared_error(y_test, y_pred_overfit)print("MSE Underfit:", mse_underfit)
print("MSE Properfit:", mse_properfit)
print("MSE Overfit:", mse_overfit)在这个示例中,我们生成了一个随机的多项式回归问题,并使用不同复杂度的线性回归模型进行拟合。通过绘制拟合结果和计算测试集上的均方误差,我们可以看到:
Underfitting(欠拟合):模型过于简单,无法捕捉数据中的复杂模式,导致在训练集和测试集上都表现不佳。
Properfitting(适当拟合):使用多项式特征的线性回归模型可以适当地拟合数据,既不过于简单也不过于复杂。
Overfitting(过拟合):模型过于复杂,对训练数据的小变化非常敏感,导致在训练集上表现良好,但在测试集上表现不佳。
通过调整模型的复杂度,我们可以在适当的范围内平衡偏差和方差,从而实现更好的泛化能力。
相关文章:

神经网络基础-神经网络补充概念-33-偏差与方差
概念 偏差(Bias): 偏差是模型预测值与实际值之间的差距,它反映了模型对训练数据的拟合能力。高偏差意味着模型无法很好地拟合训练数据,通常会导致欠拟合。欠拟合是指模型过于简单,不能捕捉数据中的复杂模式…...
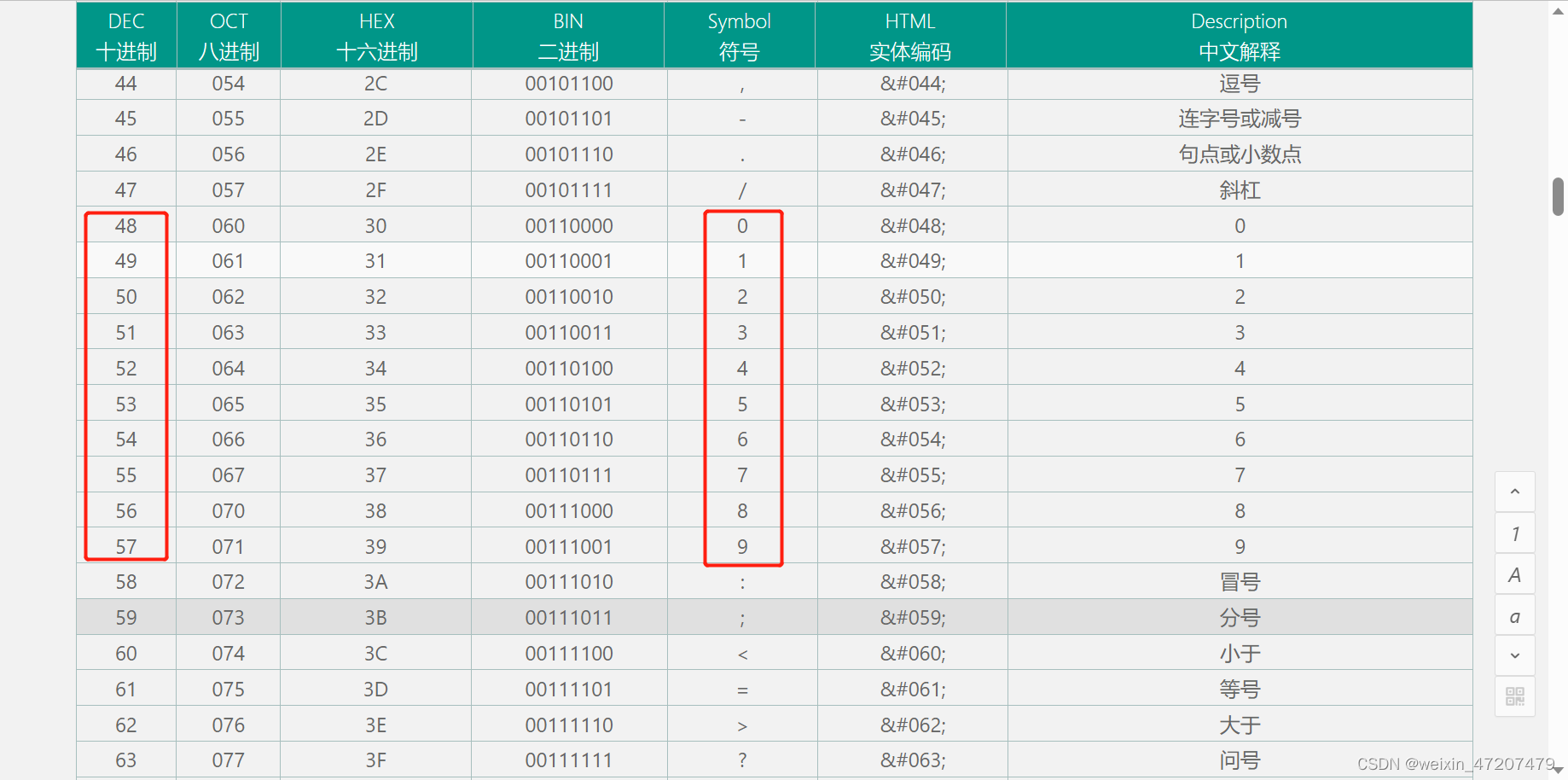
单片机第一季:零基础13——AD和DA转换
1,AD转换基本概念 51 单片机系统内部运算时用的全部是数字量,即0 和1,因此对单片机系统而言,无法直接操作模拟量,必须将模拟量转换成数字量。所谓数字量,就是用一系列0 和1 组成的二进制代码表示某个信号大…...

小区外卖跑腿,解决最后100米配送难题
小区外卖跑腿,解决最后100米配送难题 小区外卖跑腿作为新市场环境下的创业模式,通过选择小区里的闲散人员作为骑手,解决了最后100米配送的问题。这项业务不仅包括小区业主的取快递、寄快递等日常需求,还能提供小区帮忙、小区外卖…...
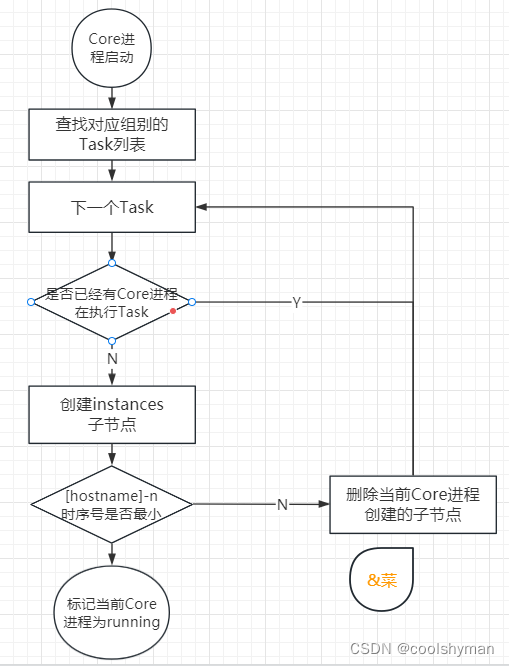
ZooKeeper的应用场景(命名服务、分布式协调通知)
3 命名服务 命名服务(NameService)也是分布式系统中比较常见的一类场景,在《Java网络高级编程》一书中提到,命名服务是分布式系统最基本的公共服务之一。在分布式系统中,被命名的实体通常可以是集群中的机器、提供的服务地址或远程对象等一这…...
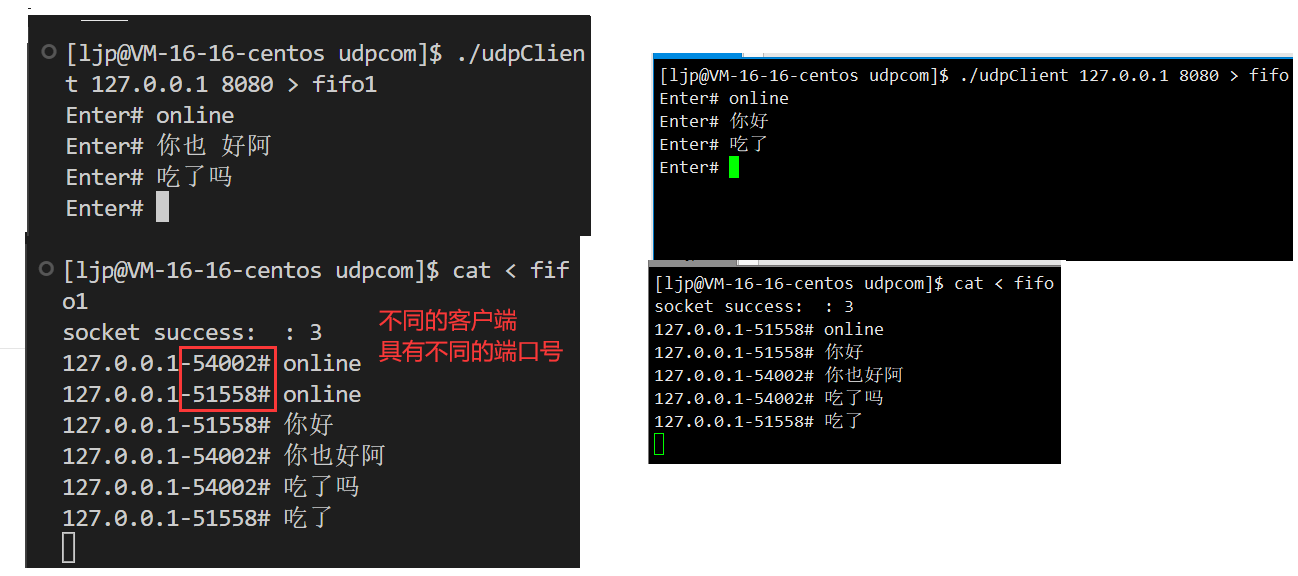
网络套接字
网络套接字 文章目录 网络套接字认识端口号初识TCP协议初识UDP协议网络字节序 socket编程接口socket创建socket文件描述符bind绑定端口号sockaddr结构体netstat -nuap:查看服务器网络信息 代码编译运行展示 实现简单UDP服务器开发 认识端口号 端口号(port)是传输层协…...

对话 4EVERLAND:Web3 是云计算的新基建吗?
在传统云计算的发展过程中,数据存储与计算的中心化问题,对用户来说一直存在着潜在的安全与隐私风险——例如单点故障可能会导致网络瘫痪和数据泄露等危险。同时,随着越来越多 Web3 项目应用的落地,对于数据云计算的性能要求也越来…...
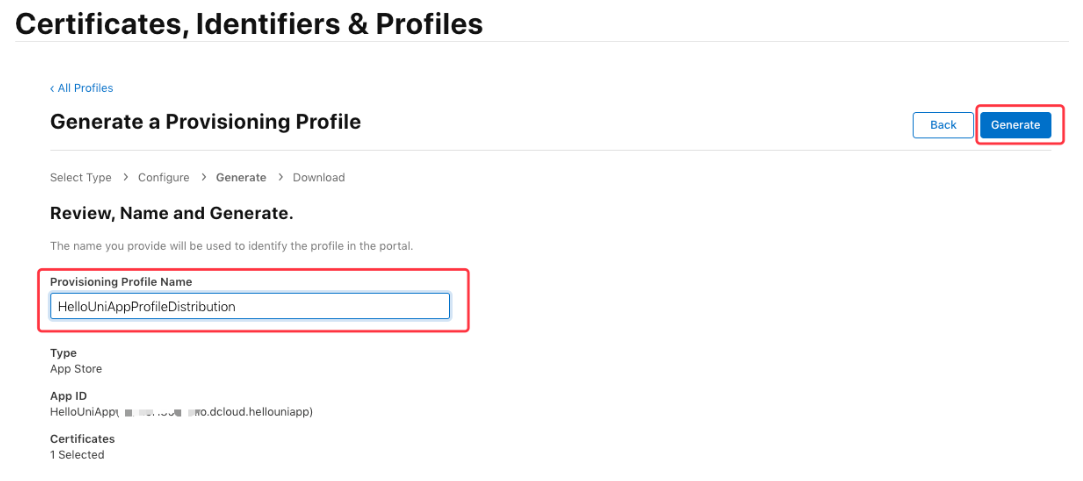
iOS申请证书(.p12)和描述文件(.mobileprovision)
打包app时,经常会用到ios证书,但很多人都苦于没有苹果电脑,即使有苹果电脑的,也会觉得苹果电脑操作也很麻烦,这里记录一下,用香蕉云编,申请证书及描述文件的过程。 香蕉云编的地址:…...

Java:PO、VO、BO、DO、DAO、DTO、POJO
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Java:PO、VO、BO、DO、DAO、DTO、POJO PO持久化对象(Persistent Object) PO是持久化对象,用于表示数据库中的实体或表…...
c语言每日一练(8)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,暑假时三天之内必有一更,到了开学之后,将看学业情…...
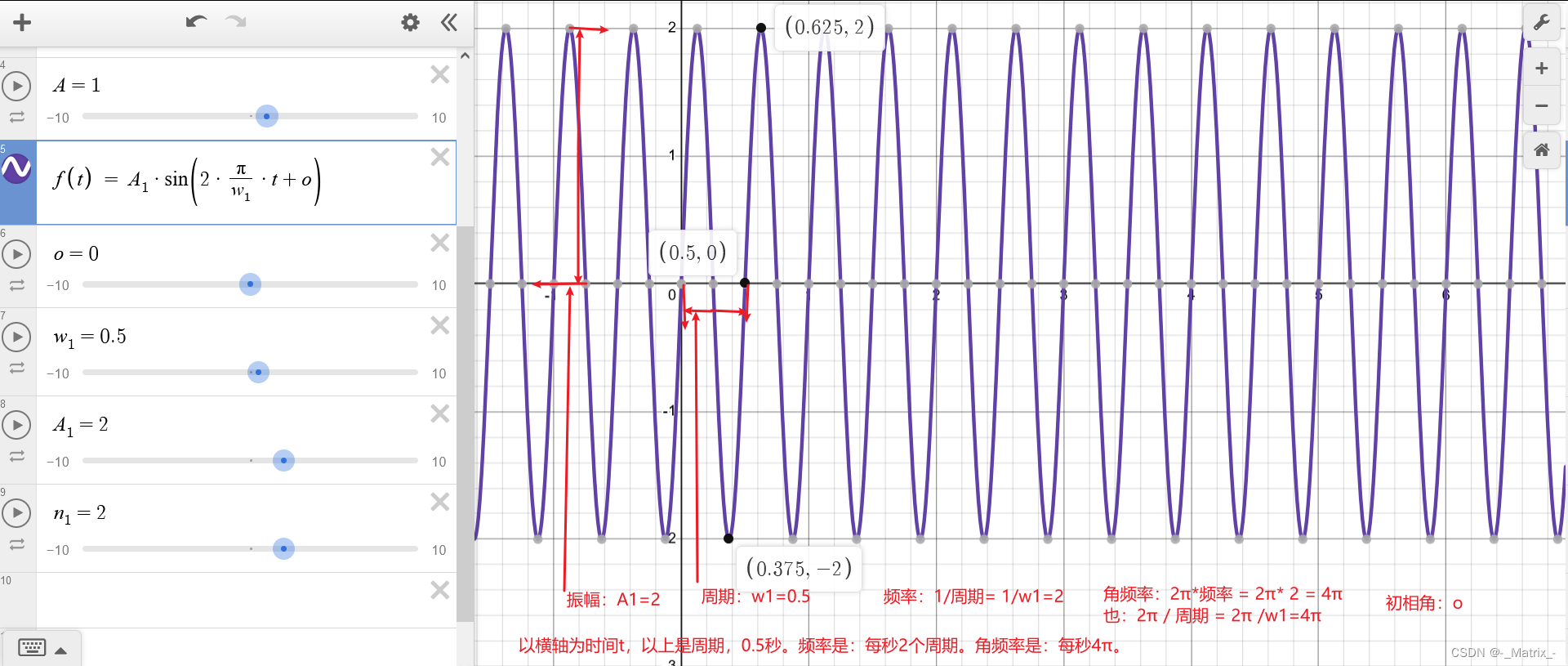
周期 角频率 频率 振幅 初相角
周期 角频率 频率 振幅 初相角 当我们谈论傅里叶级数或波形分析时,以下术语经常出现: 周期 T T T: 函数在其图形上重复的时间或空间的长度。周期的倒数是频率。 频率 f f f: 周期的倒数,即一秒内波形重复的次数。单位通常为赫兹ÿ…...

根据一棵树的两种遍历构造二叉树
题目 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 示例 1: 输入: preorder [3,9,20,15,7], inorder [9,3,15,20,7] 输出: [3,9,20,null,null,…...
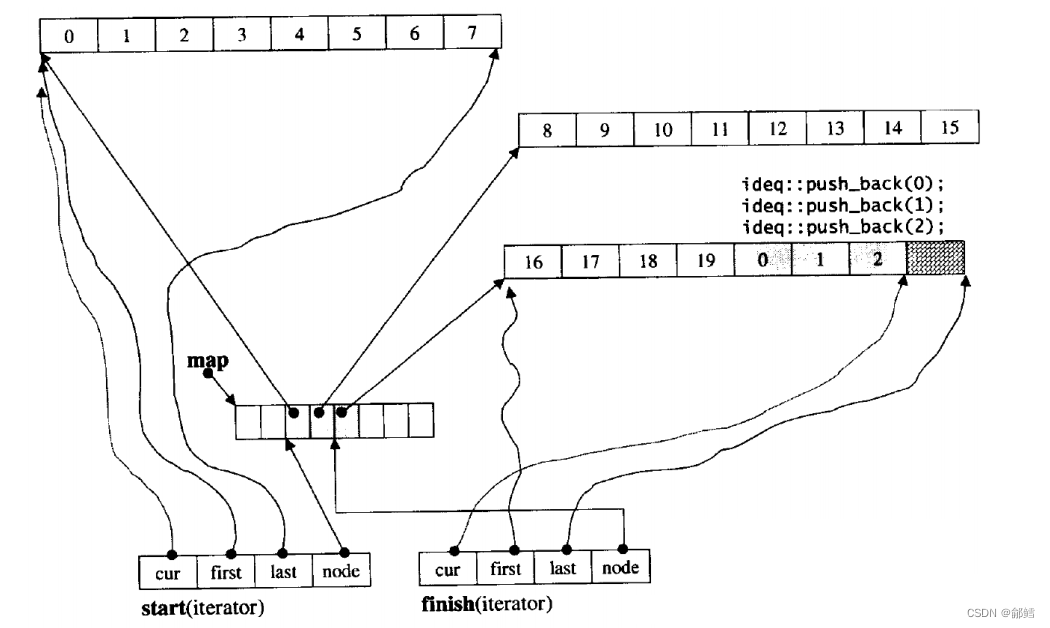
stack 、 queue的语法使用及底层实现以及deque的介绍【C++】
文章目录 stack的使用queue的使用适配器queue的模拟实现stack的模拟实现deque stack的使用 stack是一种容器适配器,具有后进先出,只能从容器的一端进行元素的插入与提取操作 #include <iostream> #include <vector> #include <stack&g…...

没学C++,如何从C语言丝滑过度到python【python基础万字详解】
大家好,我是纪宁。 文章将从C语言出发,深入介绍python的基础知识,也包括很多python的新增知识点详解。 文章目录 1.python的输入输出,重新认识 hello world,重回那个激情燃烧的岁月1.1 输出函数print的规则1.2 输入函…...

haproxy负载均衡
1、配置环境 作用环境windows测试 192.168.33.158 172.25.0.11 haproxy负载均衡haproxy:2.8.1,centos7172.25.0.31web服务器1--rs1Apache:2.4,redhat9172.25.0.32web服务器2--rs2Apache:2.4 , redhat9 2、…...
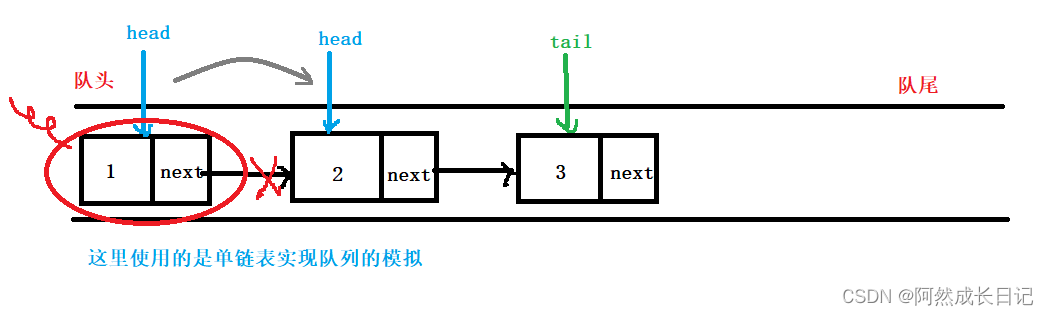
【数据结构】顺序队列模拟实现
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
TiDB数据库从入门到精通系列之六:使用 TiCDC 将 TiDB 的数据同步到 Apache Kafka
TiDB数据库从入门到精通系列之六:使用 TiCDC 将 TiDB 的数据同步到 Apache Kafka 一、技术流程二、搭建环境三、创建Kafka changefeed四、写入数据以产生变更日志五、配置 Flink 消费 Kafka 数据 一、技术流程 快速搭建 TiCDC 集群、Kafka 集群和 Flink 集群创建 c…...
Spring对象装配
在spring中,Bean的执行流程为启动spring容器,实例化bean,将bean注册到spring容器中,将bean装配到需要的类中。 既然我们需要将bea装配到需要的类中,那么如何实现呢?这篇文章,将来阐述一下如何实…...
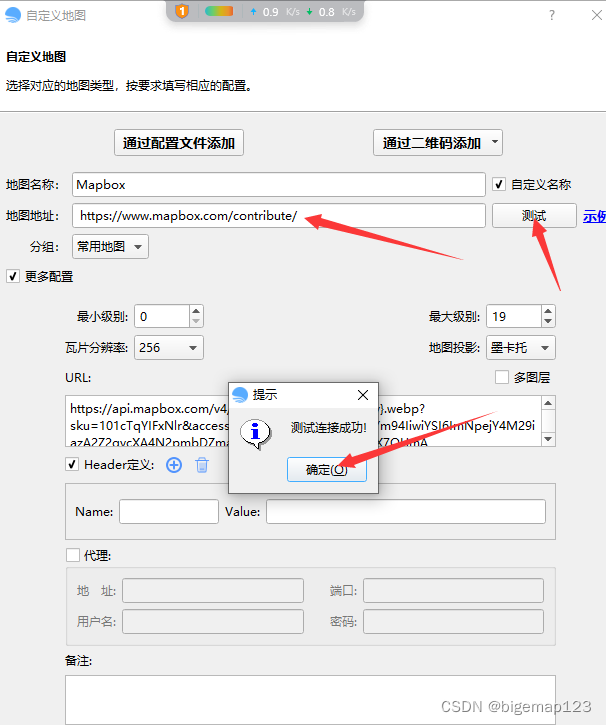
bigemap如何添加mapbox地图?
第一步 打开浏览器,找到你要访问的地图的URL地址,并且确认可以正常在浏览器中访问;浏览器中不能访问,同样也不能在软件中访问。 以下为常用地图源地址: 天地图: http://map.tianditu.gov.cn 包含&…...

python爬虫6:lxml库
python爬虫6:lxml库 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生不好…...

Linux查找命令
find find /dir -name filename 按名字查找 find . -name “*.c” 将当前目录及其子目录下所有文件后缀为 .c 的文件列出来 find . -type f 将当前目录及其子目录中的所有文件列出 find . -ctime 20 将当前目录及其子目录下所有最近 20 天内更新过的文件列出 find / -type f -…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
