PHP加密与安全的最佳实践
PHP加密与安全的最佳实践
概述
在当今信息时代,数据安全是非常重要的。对于开发人员而言,掌握加密和安全的最佳实践是必不可少的。PHP作为一种常用的后端开发语言,提供了许多功能强大且易于使用的加密和安全性相关函数和类。本文将介绍一些PHP中加密与安全的最佳实践方法,并提供相应的代码示例。
1.密码哈希
密码哈希是一种常见的保护用户密码的方法。在存储用户密码时,绝不能直接将明文密码存储在数据库中,因为一旦数据库被盗,用户的所有密码都会暴露。相反,我们应该对用户密码进行哈希处理,并存储哈希值。PHP中使用password_hash函数来进行密码哈希。下面是一个示例:

2.密码验证
在用户登录时,我们需要验证用户输入的密码是否与数据库中已存储的密码匹配。为了实现这一点,我们可以使用password_verify函数。下面是一个示例:

3.数据库安全
在与数据库交互时,我们需要确保输入的数据不会受到SQL注入攻击的影响。为了防止SQL注入攻击,我们应该使用预处理语句或绑定参数的方法来处理用户的输入。下面是一个使用预处理语句的示例:

4.防止跨站脚本攻击(XSS)
跨站脚本攻击是一种常见的攻击方式,攻击者通过在网页中注入恶意脚本来获取用户的敏感信息。为了防止XSS攻击,我们应该对从用户处接收到的数据进行过滤和转义。下面是一个示例:

5.HTTPS传输
在数据传输过程中,我们应该使用HTTPS协议来确保数据的安全传输。通过使用SSL/TLS证书来加密连接,HTTPS能够有效地防止中间人攻击和数据窃取。在PHP中,我们可以使用cURL库来进行HTTPS请求。下面是一个示例:

结论
本文介绍了PHP中加密与安全的最佳实践方法,包括密码哈希、密码验证、数据库安全、防止XSS攻击和HTTPS传输。通过应用这些最佳实践,我们可以更好地保护用户的数据安全。在实际开发中,请务必遵循这些安全原则,并根据需要进行进一步加强。
相关文章:

PHP加密与安全的最佳实践
PHP加密与安全的最佳实践 概述 在当今信息时代,数据安全是非常重要的。对于开发人员而言,掌握加密和安全的最佳实践是必不可少的。PHP作为一种常用的后端开发语言,提供了许多功能强大且易于使用的加密和安全性相关函数和类。本文将介绍一些P…...
SQL Server数据库无法连接
问题如下: 原因:sql server服务器未开启 解决方法:以管理员身份打开cmd,输入:net start mssqlserver。...

videojs 播放视频
背景:在项目中使用第三方插件videojs进行播放视频,点击事件更改播放的数据源。 一、视频相关理论 (一)、背景 网络流媒体的呈现形式分为两种:直播点播 (二)、流媒体的3种协议 分类:HTTPHLSRTMP定义:基于HTTP的流媒体…...

vue强制刷新变量
在前端开发中,我们经常需要变量的值实时响应到界面上。Vue就是一个非常强大的前端框架,它的数据绑定能够非常好地实现变量与界面的同步更新。但是有时候,我们需要强制刷新某个变量的值,以便界面能及时地反映出它的变化。本文将介绍…...

[QCA6174]QCA6174 5G WiFi DFS处理逻辑分析及雷达误检率高优化规避
DFS认证信息 WIFI DFS测试要求 Master设备需要测试的项目 4.6.2.1 Channel Availability Check 信道可用性检查 定义其作为雷达脉冲检测机制,当雷达脉冲出现时所占用的信道需要能被设备检测到已经被占用。当相关信道未被占用时,这些信道被称为Avaliable Channel可用信道 …...
预防SQL漏洞注入和规避网络攻击
前言: 虽然近些年SQL注入已经被各类的安全开发框架规避了绝大部分,但SQL注入作为一种最原始的攻击手段之一,破坏力仍然十分强大,因为它直捣黄龙数据中心。所以未雨绸缪,各位不可不重视。 预防SQL注入方法措施: 服务器…...
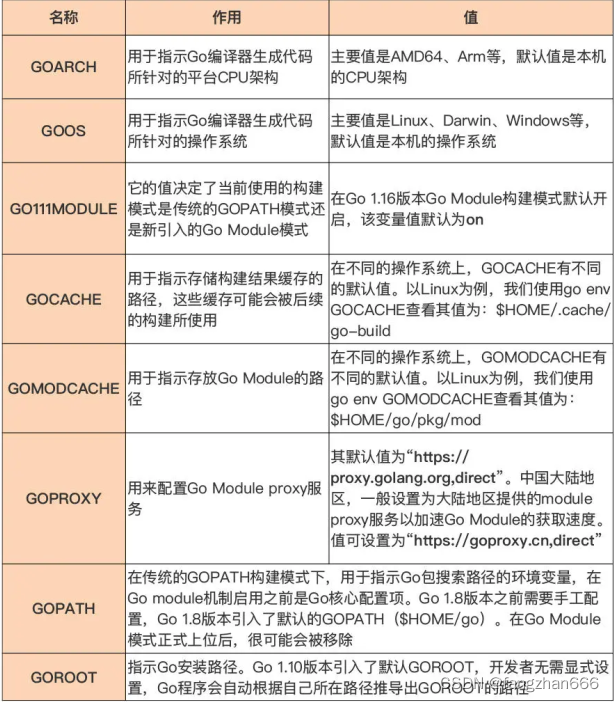
《Go 语言第一课》课程学习笔记(一)
配好环境:选择一种最适合你的 Go 安装方法 选择 Go 版本 一般情况下,建议采用最新版本。因为 Go 团队发布的 Go 语言稳定版本的平均质量一直是很高的,少有影响使用的重大 bug。可以根据不同实际项目需要或开源社区的情况使用不同的版本。 有…...
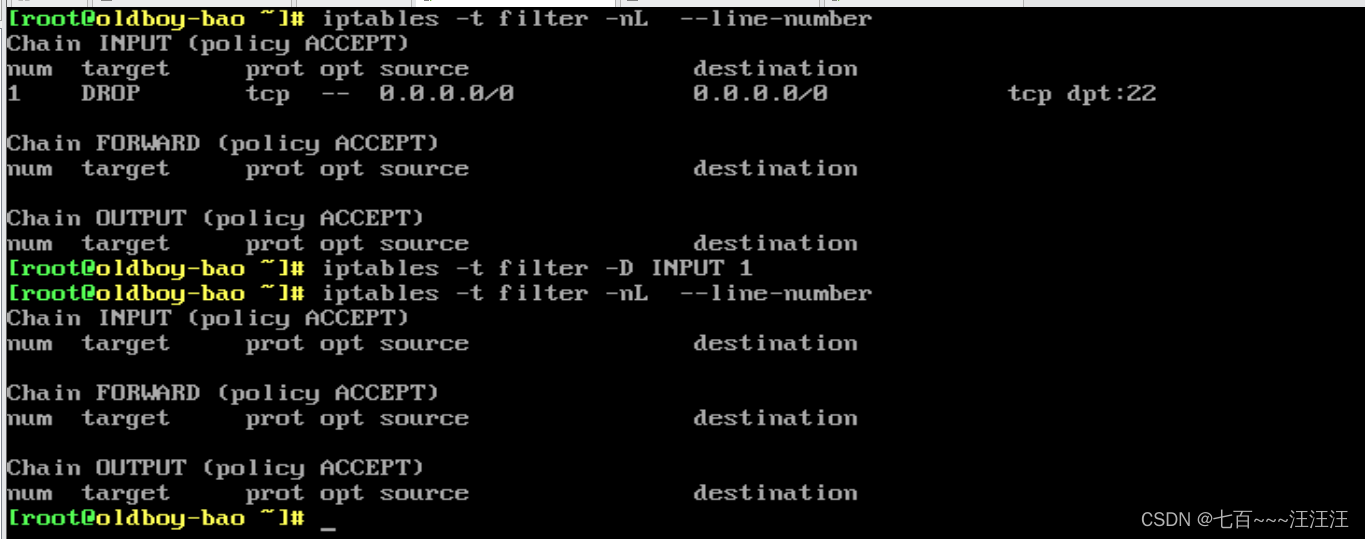
网络安全 Day29-运维安全项目-iptables防火墙
iptables防火墙 1. 防火墙概述2. 防火墙2.1 防火墙种类及使用说明2.2 必须熟悉的名词2.3 iptables 执行过程※※※※※2.4 表与链※※※※※2.4.1 简介2.4.2 每个表说明2.4.2.1 filter表 :star::star::star::star::star:2.4.2.2 nat表 2.5 环境准备及命令2.6 案例01:…...

SQL 复习 03
函数与关键字 用法说明round(x, n)四舍五入,x为浮点数,n为保留的位数ceil(x)向上取整floor(x)向下取整truncate(x, n)截断x,n为保留的位,该位之后的数值置零,位数表示示例:321.123,其中小数点前…...

出现 sudo: docker: command not found 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 未成功安装引起3.2 环境变量引起1. 问题所示 安装了docker,但是执行docker命令的时候,提示该问题: ubuntu@10-41-104-1:~$ sudo docker ps -a sudo: docker: command not foundubuntu@10-41-104-1:~$ sudo apt-get install doc…...
FastApi-1-结合sql 增/查demo
目录 FastAPI学习记录项目结构部分接口/代码展示感受全部代码 FastAPI学习记录 fastapi已经学习有一段时间,今天抽时间简单整理下。 官网介绍: FastAPI 是一个用于构建 API 的现代、快速(高性能)的 web 框架,使用 Py…...

Spring学习笔记3
使用注解开发: Component 组件开发相当于 Value(“xxx”)可以对属性进行赋值 package pojo;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component; //等价于<bean id"user" class"po…...

springboot艰难版本升级之路!! springboot 2.3.x版本升级到2.7.x版本
文章目录 1.缘起1.1 升级到版本2.7.12启动失败,而且没有报错信息1.2 application-dev.yml 配置加载问题1.3 openfeign依赖问题汇总1.4 datasource报错1.5 MySQL驱动升级1.6 循环依赖报错1.7 跨域错误临时总结1.缘起 由于服务需要搭建链路追踪, 需要把springboot版本升级到2.7.1…...

Codeforces 1856E2 复杂度分析 + DP
题意 传送门 Codeforces 1856E2 PermuTree (hard version) 题解 可以独立考虑每一个固定的 p l c a ( u , v ) plca(u,v) plca(u,v) 对答案的贡献。可以观察到,对于 p p p 的每一棵子树,其所有节点在最优情况下仅有 a p < a v a_p < a_v ap…...

Windows - UWP - 为UWP应用创建桌面快捷方式
Windows - UWP - 为UWP应用创建桌面快捷方式 前言 这是一个较为简单的方式,不需要过多的命令行。 How 首先Win R -> shell:AppsFolder -> 回车, 这将显示电脑上的已安装应用(Win32 & UWP): 找到想要创建…...

了解Web DDoS海啸攻击的4个维度
我们都知道近年来网络攻击的数量和频率急剧上升,针对Web应用程序的DDoS海啸攻击就是其中增长非常迅速的一个种类。过去常见的HTTP/S洪水攻击正在大范围的转变为更难对付的Web DDoS海啸攻击,每个人都应该提前做好被攻击的准备并采取适当的保护措施。 哪些…...
【数学建模】逻辑回归算法(Logistic Resgression)
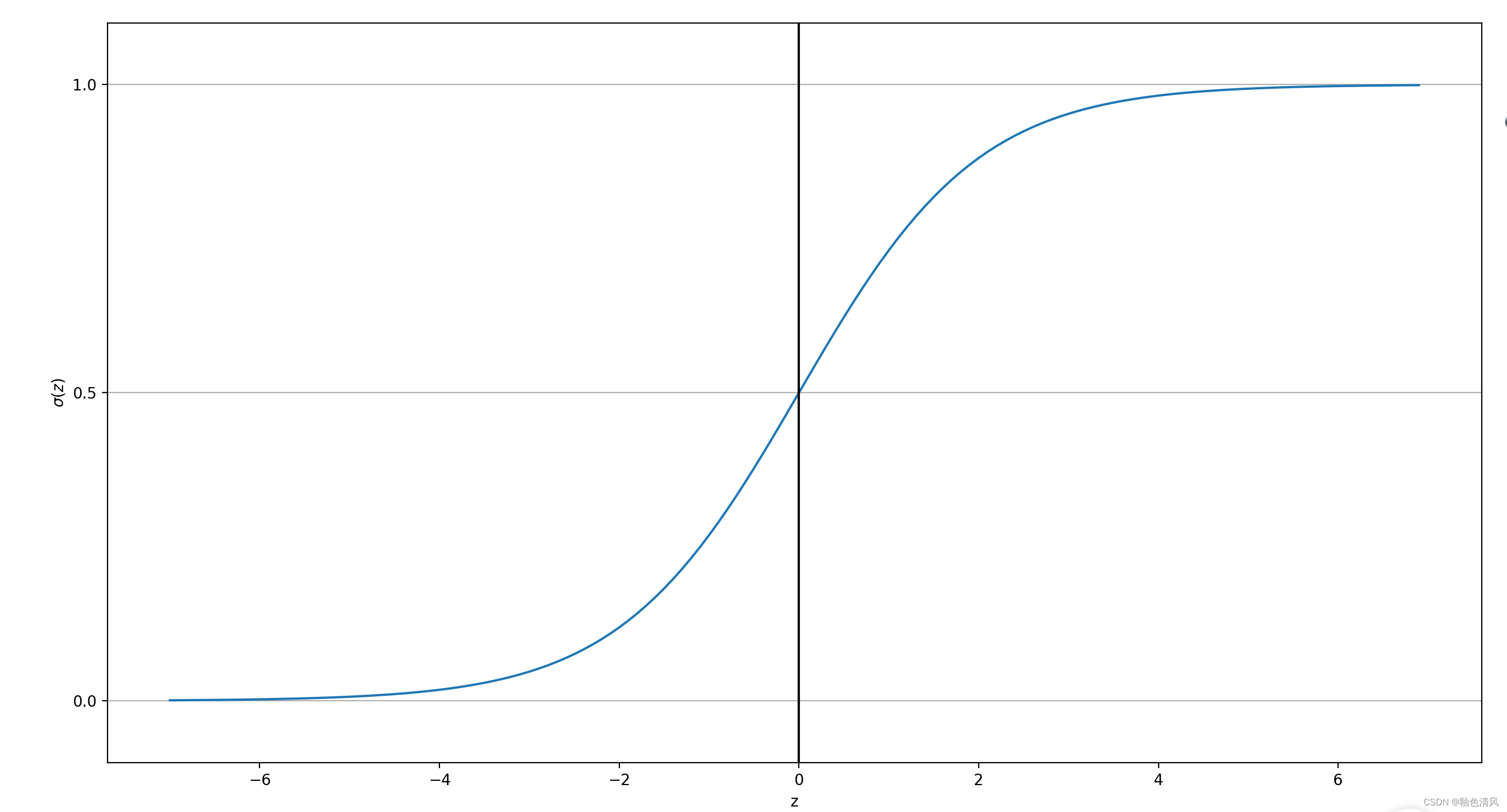
逻辑回归算法 简介逻辑回归与条件概率绘制sigmoid函数 简介 逻辑回归算法是一种简单但功能强大的二元线性分类算法。需要注意的是,尽管"逻辑回归"名字带有“回归”二字,但逻辑回归是一个分类算法,而不是回归算法。 我认为ÿ…...

Hadoop HA集群两个NameNode都是standby或者主NameNode是standby,从NameNode是active的情况集锦
文章目录 背景架构HDFS HA配置错误原因解决方案方案一方案二方案三(首先查看自己各参数文件是否配置出错) 后记补充failovertransitionToActive 常用端口号及配置文件常用端口号hadoop3.xhadoop2.x 常用配置文件 这里说一下配置Hadoop HA集群可能出现的两…...
[Go版]算法通关村第十一关白银——位运算的高频算法题
目录 专题1:位移的妙用题目:位1的个数(也被称为汉明重量)解法1:遍历所有位,判断每个位的数字是否是1Go代码 解法2:依次消除每个1的位 numnum&(num-1)Go代码 题目:比特位计数思路…...

Swift 基础
工程目录 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 点击下载代码:swift-01...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
