【傅里叶级数与傅里叶变换】数学推导——1、基础知识点回顾及[Part1:三角函数的正交性]介绍
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。
文章全部链接:
基础知识点
Part1:三角函数系的正交性
Part2:T=2π的周期函数的傅里叶级数展开
Part3:周期为T=2L的函数展开
Part4:傅里叶级数的复数形式
Part5:从傅里叶级数推导傅里叶变换
总结
文章目录
- 基础知识点
- Part1:三角函数系的正交性
基础知识点
设 α \alpha α为任意角
f ( 2 k π + α ) = f α ( k ∈ Z ) ,其中 f 为 s i n 或 c o s 或 t a n 或 c o t s i n ( π + α ) = − s i n α c o s ( π + α ) = − c o s α t a n ( π + α ) = t a n α c o t ( π + α ) = c o t α s i n ( − α ) = − s i n α c o s ( − α ) = c o s α t a n ( π + α ) = − t a n α c o t ( π + α ) = − c o t α s i n ( π − α ) = s i n α c o s ( π − α ) = − c o s α t a n ( π − α ) = − t a n α c o t ( π − α ) = − c o t α s i n ( 2 π − α ) = − s i n α c o s ( 2 π − α ) = c o s α t a n ( 2 π − α ) = − t a n α c o t ( 2 π − α ) = − c o t α \begin{align} & f(2k \pi + \alpha) = f \alpha (k \in Z) ,其中f为 sin或cos或tan或cot \\ \\ & sin(\pi + \alpha) = -sin \alpha \\ & cos(\pi + \alpha) = -cos \alpha \\ & tan(\pi + \alpha) = tan \alpha \\ & cot(\pi + \alpha) = cot \alpha \\ \\ & sin(- \alpha) = - sin \alpha \\ & cos(- \alpha) = cos \alpha \\ & tan(\pi + \alpha) = -tan \alpha \\ & cot(\pi + \alpha) = -cot \alpha \\ \\ & sin(\pi - \alpha) = sin \alpha \\ & cos(\pi - \alpha) = - cos \alpha \\ & tan(\pi - \alpha) = - tan \alpha \\ & cot(\pi - \alpha) = -cot \alpha \\ \\ & sin(2 \pi - \alpha) = -sin \alpha \\ & cos(2 \pi - \alpha) = cos \alpha \\ & tan(2 \pi - \alpha) = -tan \alpha \\ & cot(2 \pi - \alpha) = -cot \alpha & \end{align} f(2kπ+α)=fα(k∈Z),其中f为sin或cos或tan或cotsin(π+α)=−sinαcos(π+α)=−cosαtan(π+α)=tanαcot(π+α)=cotαsin(−α)=−sinαcos(−α)=cosαtan(π+α)=−tanαcot(π+α)=−cotαsin(π−α)=sinαcos(π−α)=−cosαtan(π−α)=−tanαcot(π−α)=−cotαsin(2π−α)=−sinαcos(2π−α)=cosαtan(2π−α)=−tanαcot(2π−α)=−cotα
积化和差公式:
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 cos α sin β = sin ( α + β ) − sin ( α − β ) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2 sin α sin β = − cos ( α + β ) − cos ( α − β ) 2 \begin{align} & \sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2} \\ & \cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2} \\ & \cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}\\ & \sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2} & \end{align} sinαcosβ=2sin(α+β)+sin(α−β)cosαsinβ=2sin(α+β)−sin(α−β)cosαcosβ=2cos(α+β)+cos(α−β)sinαsinβ=−2cos(α+β)−cos(α−β)
和差化积公式:
s i n α + s i n β = 2 s i n α + β 2 c o s α − β 2 s i n α − s i n β = 2 c o s α + β 2 s i n α − β 2 c o s α + c o s β = 2 c o s α + β 2 c o s α − β 2 c o s α − c o s β = − 2 s i n α + β 2 s i n α − β 2 \begin{align} & sin \alpha + sin \beta = 2sin\frac {\alpha + \beta} {2} cos \frac {\alpha - \beta} {2} \\ & sin \alpha - sin \beta = 2cos\frac {\alpha + \beta} {2} sin \frac {\alpha - \beta} {2} \\ & cos \alpha + cos \beta = 2 cos\frac {\alpha + \beta} {2} cos \frac {\alpha - \beta} {2} \\ & cos \alpha - cos \beta = - 2 sin\frac {\alpha + \beta} {2} sin \frac {\alpha - \beta} {2} & \end{align} sinα+sinβ=2sin2α+βcos2α−βsinα−sinβ=2cos2α+βsin2α−βcosα+cosβ=2cos2α+βcos2α−βcosα−cosβ=−2sin2α+βsin2α−β
倍角公式:
s i n 2 α = s i n α c o s α + s i n α c o s α = 2 s i n α c o s α c o s 2 α = c o s 2 α − s i n 2 α = 2 c o s 2 α − 1 = 1 − 2 s i n 2 α c o s 2 α = 1 + c o s 2 α 2 s i n 2 α = 1 − c o s 2 α 2 t a n 2 α = 2 t a n α 1 − t a n 2 α \begin{align} & sin 2 \alpha = sin \alpha cos \alpha + sin \alpha cos \alpha = 2 sin \alpha cos \alpha \\ & cos 2 \alpha = cos^2 \alpha - sin ^2 \alpha =2 cos ^ 2 \alpha -1 = 1- 2 sin^2 \alpha \\ & cos ^ 2 \alpha = \frac{1 + cos 2 \alpha}{2} \\ & sin^ 2 \alpha = \frac{1 - cos 2 \alpha}{2} \\ & tan 2 \alpha = \frac {2 tan \alpha} {1 - tan ^2 \alpha} & \end{align} sin2α=sinαcosα+sinαcosα=2sinαcosαcos2α=cos2α−sin2α=2cos2α−1=1−2sin2αcos2α=21+cos2αsin2α=21−cos2αtan2α=1−tan2α2tanα
三角函数导数:
正弦函数: ( s i n x ) ′ = c o s x 余弦函数: ( c o s x ) ′ = − s i n x 正切函数: ( t a n x ) ′ = s e c 2 x 余切函数: ( c o t x ) ′ = − c s c 2 x \begin{align} & 正弦函数: (sin x)' = cosx \\ & 余弦函数: (cos x)' = -sinx \\ & 正切函数: (tan x )' = sec^2 x \\ & 余切函数: (cot x)' = -csc^2x & \end{align} 正弦函数:(sinx)′=cosx余弦函数:(cosx)′=−sinx正切函数:(tanx)′=sec2x余切函数:(cotx)′=−csc2x
积分性质:
性质 1 :如果 c 是常数, ∫ a b c d x = c ( b − a ) ; 性质 2 :如果 c 是常数, ∫ z b c f ( x ) d x = c ∫ a b f ( x ) d x ; 性质 3 : ∫ a b [ f ( x ) ± g ( x ) ] d x = ∫ a b f ( x ) d x ± ∫ z b g ( x ) d x ; \begin{align} & 性质1:如果c是常数,\int_{a}^{b} cdx = c(b-a); \\ & 性质2:如果c是常数,\int_z^b cf(x)dx = c \int_a^b f(x)dx; \\ & 性质3:\int_{a}^{b}[f(x) \pm g(x)] dx = \int_a^b f(x)dx \pm \int_z^b g(x)dx; & \end{align} 性质1:如果c是常数,∫abcdx=c(b−a);性质2:如果c是常数,∫zbcf(x)dx=c∫abf(x)dx;性质3:∫ab[f(x)±g(x)]dx=∫abf(x)dx±∫zbg(x)dx;
Part1:三角函数系的正交性
三角函数系集合: { 0 , 1 , s i n x , c o s x , s i n 2 x , c o s 2 x , . . . , s i n n x , c o s n x , . . . } \{0,1,sin x, cos x, sin 2x, cos 2x, ...,sin nx, cos nx, ...\} {0,1,sinx,cosx,sin2x,cos2x,...,sinnx,cosnx,...},即为 { s i n n x , c o s n x } \{sin nx, cos nx\} {sinnx,cosnx},其中 n = 0 , 1 , 2 , . . . n = 0, 1,2,... n=0,1,2,...。
对于两个向量 a ⃗ \vec{a} a和 b ⃗ \vec {b} b,如果它们的内积等于0,表示这两个向量是垂直的,具有正交性。即 a ⃗ ⋅ b ⃗ = 0 \vec{a} \cdot \vec{b} = 0 a⋅b=0,如下示意图, a ⃗ ⋅ b ⃗ = 2 ∗ − 1 + 1 ∗ 2 = 0 \vec{a} \cdot \vec{b} = 2*-1 + 1*2 = 0 a⋅b=2∗−1+1∗2=0。
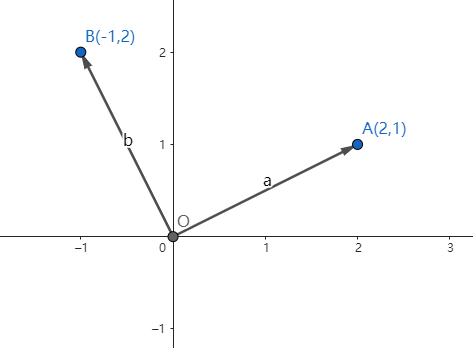
若向量 a ⃗ \vec{a} a和向量 b ⃗ \vec{b} b中包含三个元素,分别是 ( a 1 , a 2 , a 3 ) (a_1, a_2, a_3) (a1,a2,a3)和 ( b 1 , b 2 , b 3 ) (b_1, b_2, b_3) (b1,b2,b3),如果 a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + a 3 b 3 = 0 \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 = 0 a⋅b=a1b1+a2b2+a3b3=0,那么 a ⃗ \vec{a} a与 b ⃗ \vec {b} b正交。
再推广到 a ⃗ \vec a a和 b ⃗ \vec b b中有 n n n个元素,分别为 { a 1 , a 2 , a 3 , . . . , a n } \{ a_1, a_2, a_3, ..., a_n \} {a1,a2,a3,...,an}和 { b 1 , b 2 , b 3 , . . . , b n } \{ b_1, b_2, b_3, ... , b_n \} {b1,b2,b3,...,bn},如果 a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + a 3 b 3 + . . a n b n = ∑ i = 1 n a i b i = 0 \vec a \cdot \vec b = a_1 b_1 + a_2 b_2 + a_3 b_3 + .. a_n b_n = \sum_{i=1} ^ {n} a_i b_i = 0 a⋅b=a1b1+a2b2+a3b3+..anbn=∑i=1naibi=0,那么 a ⃗ \vec a a与 b ⃗ \vec b b正交。
再扩展,如果 a = f ( x ) a = f(x) a=f(x), b = g ( x ) b = g(x) b=g(x),在一个区间内如 [ x 0 , x 1 ] [x_0, x_1] [x0,x1]计算 a ⋅ b a \cdot b a⋅b即 f ( x ) ⋅ g ( x ) f(x) \cdot g(x) f(x)⋅g(x),也就是计算在区间 [ x 0 , x 1 ] [x_0, x_1] [x0,x1]内的面积和,相当于求积分 ∫ x 0 x 1 f ( x ) g ( x ) d x \int_{x_0}^{x_1} f(x) g(x)dx ∫x0x1f(x)g(x)dx。如果 ∫ x 0 x 1 f ( x ) g ( x ) d x = 0 \int_{x_0}^{x_1} f(x) g(x)dx=0 ∫x0x1f(x)g(x)dx=0,就可以说 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)这两个函数正交。
再说回到三角函数的正交性的定义:从三角函数系集合中任取两项,在 [ − π , π ] [-\pi, \pi] [−π,π]之间,这两项的积分等于0。
即:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 ∫ − π π s i n ( n x ) s i n ( m x ) d x = 0 ∫ − π π c o s ( n x ) c o s ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = 0 & \end{align} ∫−ππsin(nx)cos(mx)dx=0∫−ππcos(nx)sin(mx)dx=0∫−ππsin(nx)sin(mx)dx=0∫−ππcos(nx)cos(mx)dx=0
接下来证明三角函数的正交性。
当 m ≠ n m \ne n m=n时,由积化和差公式 s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin \alpha cos \beta = \frac{1}{2} [sin(\alpha + \beta) + sin(\alpha - \beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 1 2 [ ∫ − π π s i n ( n + m ) x d x + ∫ − π π s i n ( n − m ) x d x ] = 1 2 [ ( − 1 n + m c o s ( n + m ) x ∣ − π π ) + ( − 1 n − m c o s ( n − m ) x ∣ − π π ) ] = 1 2 [ ( − 1 n + m ) [ c o s ( n + m ) π − c o s ( − ( n + m ) π ) ] + ( − 1 n − m ) [ c o s ( n − m ) π − c o s ( − ( n − m ) π ) ] ] 有 c o s ( − α ) = c o s α ,很容易得出上式为 0 , 即: ∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 \begin{align} &\int_{- \pi}^{\pi} sin (nx) cos (mx) dx \\ & = \frac {1}{2} \left [ \int_{- \pi}^{\pi} sin(n + m)x dx + \int_{- \pi}^{\pi}sin(n-m)x dx \right] \\ & = \frac{1}{2} \left[ (- \frac{1}{n+m} cos(n+m)x |_{- \pi}^{\pi}) + (- \frac{1}{n-m} cos(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [(- \frac{1}{n+m}) \left[ cos(n+m) \pi - cos(-(n+m)\pi) \right] + (- \frac{1}{n-m} ) \left[ cos(n-m) \pi - cos(-(n-m)\pi) \right] \right ] \\ & 有cos (-\alpha) = cos \alpha,很容易得出上式为0 , 即: \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 & \end{align} ∫−ππsin(nx)cos(mx)dx=21[∫−ππsin(n+m)xdx+∫−ππsin(n−m)xdx]=21[(−n+m1cos(n+m)x∣−ππ)+(−n−m1cos(n−m)x∣−ππ)]=21[(−n+m1)[cos(n+m)π−cos(−(n+m)π)]+(−n−m1)[cos(n−m)π−cos(−(n−m)π)]]有cos(−α)=cosα,很容易得出上式为0,即:∫−ππsin(nx)cos(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 c o s α s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] cos\alpha sin\beta = \frac{1}{2} [sin(\alpha + \beta) - sin(\alpha - \beta)] cosαsinβ=21[sin(α+β)−sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) s i n ( m x ) d x = 1 2 [ ∫ − π π s i n ( n + m ) x d x − ∫ − π π s i n ( n − m ) x d x ] = 1 2 [ ( − 1 n + m ) c o s ( n + m ) x ∣ − π π ) − ( − 1 n − m ) c o s ( n − m ) x ∣ − π π ) ] = 1 2 [ ( − 1 n + m ) [ c o s ( n + m ) π − c o s ( − ( n + m ) π ) ] − ( − 1 n − m ) [ c o s ( n − m ) π − c o s ( − ( n − m ) π ) ] ] 有 c o s ( − α ) = c o s α ,很容易得出上式为 0 , 即: ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx \\ & =\frac {1}{2} \left [ \int_{- \pi}^{\pi} sin(n + m)x dx - \int_{- \pi}^{\pi}sin(n-m)x dx \right] \\ & = \frac{1}{2} \left[ (- \frac{1}{n+m}) cos(n+m)x |_{- \pi}^{\pi}) - (- \frac{1}{n-m} )cos(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [(- \frac{1}{n+m}) \left[ cos(n+m) \pi - cos(-(n+m)\pi) \right] - (- \frac{1}{n-m} ) \left[ cos(n-m) \pi - cos(-(n-m)\pi) \right] \right ] \\ & 有cos (-\alpha) = cos \alpha,很容易得出上式为0 , 即: \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 & \end{align} ∫−ππcos(nx)sin(mx)dx=21[∫−ππsin(n+m)xdx−∫−ππsin(n−m)xdx]=21[(−n+m1)cos(n+m)x∣−ππ)−(−n−m1)cos(n−m)x∣−ππ)]=21[(−n+m1)[cos(n+m)π−cos(−(n+m)π)]−(−n−m1)[cos(n−m)π−cos(−(n−m)π)]]有cos(−α)=cosα,很容易得出上式为0,即:∫−ππcos(nx)sin(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 c o s α c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] cos\alpha cos\beta = \frac{1}{2} [cos(\alpha + \beta) + cos(\alpha - \beta)] cosαcosβ=21[cos(α+β)+cos(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) c o s ( m x ) d x = 1 2 [ ∫ − π π c o s ( n + m ) x d x + ∫ − π π c o s ( n − m ) x d x ] = 1 2 [ 1 n + m s i n ( n + m ) x ∣ − π π ) + 1 n − m s i n ( n − m ) x ∣ − π π ) ] = 1 2 [ 1 n + m [ s i n ( n + m ) π − s i n ( − ( n + m ) π ) ] + 1 n − m [ s i n ( n − m ) π − s i n ( − ( n − m ) π ) ] ] 有 s i n ( − α ) = − s i n α , 又有 ∣ s i n k π + α ∣ = ∣ s i n α ∣ , 上式中 α = 0 , s i n ( ( n + m ) ) π = s i n ( ( n − m ) π ) = 0 很容易得出上式为 0 , 即: ∫ − π π c o s ( n x ) c o s ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx \\ &=\frac {1}{2} \left [ \int_{- \pi}^{\pi} cos(n + m)x dx + \int_{- \pi}^{\pi}cos(n-m)x dx \right] \\ & = \frac{1}{2} \left[ \frac{1}{n+m} sin(n+m)x |_{- \pi}^{\pi}) + \frac{1}{n-m} sin(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [ \frac{1}{n+m} \left[ sin(n+m) \pi - sin(-(n+m)\pi) \right] + \frac{1}{n-m} \left[ sin(n-m) \pi - sin(-(n-m)\pi) \right] \right ] \\ & 有 sin (-\alpha) = - sin \alpha,又有|sin k \pi + \alpha| = |sin \alpha|,\\ & 上式中\alpha=0, sin ( (n+m)) \pi = sin((n-m) \pi) = 0很容易得出上式为0 , 即: \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = 0 & \end{align} ∫−ππcos(nx)cos(mx)dx=21[∫−ππcos(n+m)xdx+∫−ππcos(n−m)xdx]=21[n+m1sin(n+m)x∣−ππ)+n−m1sin(n−m)x∣−ππ)]=21[n+m1[sin(n+m)π−sin(−(n+m)π)]+n−m1[sin(n−m)π−sin(−(n−m)π)]]有sin(−α)=−sinα,又有∣sinkπ+α∣=∣sinα∣,上式中α=0,sin((n+m))π=sin((n−m)π)=0很容易得出上式为0,即:∫−ππcos(nx)cos(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 s i n α s i n β = 1 2 [ c o s ( α + β ) − c o s ( α − β ) ] sin\alpha sin\beta = \frac{1}{2} [cos(\alpha + \beta) - cos(\alpha - \beta)] sinαsinβ=21[cos(α+β)−cos(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) s i n ( m x ) d x = 1 2 [ ∫ − π π c o s ( n + m ) x d x − ∫ − π π c o s ( n − m ) x d x ] = 1 2 [ 1 n + m s i n ( n + m ) x ∣ − π π ) − 1 n − m s i n ( n − m ) x ∣ − π π ) ] = 1 2 [ 1 n + m [ s i n ( n + m ) π − s i n ( − ( n + m ) π ) ] − 1 n − m [ s i n ( n − m ) π − s i n ( − ( n − m ) π ) ] ] 有 ∣ s i n ( k π + α ) ∣ = ∣ s i n α ∣ , 上式中 α = 0 , s i n ( ( n + m ) ) π = s i n ( ( n − m ) π ) = 0 很容易得出上式为 0 , 即: ∫ − π π s i n ( n x ) s i n ( m x ) d x = 0 \begin{align} \int_{- \pi}^{\pi} sin (nx) sin (mx) dx &=\frac {1}{2} \left [ \int_{- \pi}^{\pi} cos(n + m)x dx - \int_{- \pi}^{\pi}cos(n-m)x dx \right] \\ & = \frac{1}{2} \left[ \frac{1}{n+m} sin(n+m)x |_{- \pi}^{\pi}) - \frac{1}{n-m} sin(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [ \frac{1}{n+m} \left[ sin(n+m) \pi - sin(-(n+m)\pi) \right] - \frac{1}{n-m} \left[ sin(n-m) \pi - sin(-(n-m)\pi) \right] \right ] \\ & 有 | sin (k \pi + \alpha)| = | sin \alpha |, 上式中\alpha=0, sin ( (n+m)) \pi = sin( (n-m) \pi) = 0很容易得出上式为0 , 即: \\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = 0 & \end{align} ∫−ππsin(nx)sin(mx)dx=21[∫−ππcos(n+m)xdx−∫−ππcos(n−m)xdx]=21[n+m1sin(n+m)x∣−ππ)−n−m1sin(n−m)x∣−ππ)]=21[n+m1[sin(n+m)π−sin(−(n+m)π)]−n−m1[sin(n−m)π−sin(−(n−m)π)]]有∣sin(kπ+α)∣=∣sinα∣,上式中α=0,sin((n+m))π=sin((n−m)π)=0很容易得出上式为0,即:∫−ππsin(nx)sin(mx)dx=0
当 m = n m=n m=n时, 由三角函数平方公式 s i n 2 α = 1 2 ( 1 − c o s 2 α ) sin ^ 2 \alpha = \frac{1}{2} (1 - cos 2 \alpha) sin2α=21(1−cos2α)、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) s i n ( n x ) d x = 1 2 [ ∫ − π π ( 1 − c o s 2 n x ) d x ] = 1 2 [ ∫ − π π 1 d x − ∫ − π π c o s 2 n x d x ] 如果 m = n = 0 ,上式 = 0 ; 如果 m = n ≠ 0 , 可以假定 c o s 2 n x = c o s 0 x c o s 2 n x , 根据三角函数的正交性质,那么右边 ∫ − π π c o s 2 n x d x = 0 ,上式即为 1 2 [ x ∣ − π π ] = 1 2 2 π = π \begin{align} &\int_{-\pi}^{\pi} sin (nx) sin (nx) dx = \frac{1}{2} \left [ \int_{-\pi}^{\pi} (1 - cos2nx) dx \right ] = \frac{1}{2} \left [ \int_{-\pi}^{\pi} 1 dx - \int_{-\pi}^{\pi} cos2nx dx \right ] \\ & 如果m=n=0,上式=0;\\ & 如果m=n \ne 0, 可以假定cos2nx = cos 0x cos 2nx,\\ & 根据三角函数的正交性质,那么右边\int_{-\pi}^{\pi} cos2nx dx = 0 ,上式即为 \\ & \frac{1}{2} \left[ x|_{-\pi}^{\pi}\right] = \frac{1}{2} 2\pi = \pi & \end{align} ∫−ππsin(nx)sin(nx)dx=21[∫−ππ(1−cos2nx)dx]=21[∫−ππ1dx−∫−ππcos2nxdx]如果m=n=0,上式=0;如果m=n=0,可以假定cos2nx=cos0xcos2nx,根据三角函数的正交性质,那么右边∫−ππcos2nxdx=0,上式即为21[x∣−ππ]=212π=π
当 m = n m=n m=n时, 由三角函数平方公式 c o s 2 α = 1 2 ( 1 + c o s 2 α ) cos^ 2 \alpha = \frac{1}{2} (1 + cos 2 \alpha) cos2α=21(1+cos2α)、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) c o s ( n x ) d x = 1 2 [ ∫ − π π ( 1 + c o s 2 n x ) d x ] = 1 2 [ ∫ − π π 1 d x + ∫ − π π c o s 2 n x d x ] 如果 m = n = 0 ,上式变为 1 2 [ ∫ − π π 2 d x ] = x ∣ − π π = 2 π ; 如果 m = n ≠ 0 , 假定 c o s 2 n x = c o s 0 x c o s 2 n x ,根据三角函数的正交性质, 那么右边 ∫ − π π c o s 2 n x d x = 0 ,上式即为 1 2 [ x ∣ − π π ] = 1 2 2 π = π \begin{align} & \int_{-\pi}^{\pi} cos (nx) cos (nx) dx = \frac{1}{2} \left [ \int_{-\pi}^{\pi} (1 + cos2nx) dx \right ] = \frac{1}{2} \left [ \int_{-\pi}^{\pi} 1 dx + \int_{-\pi}^{\pi} cos2nx dx \right ] \\ & 如果m=n=0,上式变为\frac{1}{2} \left [ \int_{-\pi}^{\pi} 2 dx \right ] = x|_{-\pi}^{\pi} = 2\pi;\\ & 如果m=n \ne 0, 假定cos2nx = cos 0x cos 2nx,根据三角函数的正交性质,\\ & 那么右边\int_{-\pi}^{\pi} cos2nx dx = 0 ,上式即为 \\ & \frac{1}{2} \left[ x|_{-\pi}^{\pi}\right] = \frac{1}{2} 2\pi = \pi & \end{align} ∫−ππcos(nx)cos(nx)dx=21[∫−ππ(1+cos2nx)dx]=21[∫−ππ1dx+∫−ππcos2nxdx]如果m=n=0,上式变为21[∫−ππ2dx]=x∣−ππ=2π;如果m=n=0,假定cos2nx=cos0xcos2nx,根据三角函数的正交性质,那么右边∫−ππcos2nxdx=0,上式即为21[x∣−ππ]=212π=π
当 m = n m=n m=n时, 由积化和差公式 s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin \alpha cos \beta = \frac{1}{2} [sin(\alpha + \beta) + sin(\alpha - \beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) c o s ( n x ) d x = ∫ − π π c o s ( n x ) s i n ( n x ) d x = 1 2 [ ∫ − π π s i n 2 n x d x + ∫ − π π s i n 0 x d x ] 当 m = n = 0 时,左边变为 ∫ − π π 0 d x = 0 ,右边计算也为 0 ,所以 ∫ − π π s i n ( n x ) c o s ( n x ) d x = 0 当 m = n ≠ 0 时,左边可以看作 ∫ − π π c o s 0 x s i n 2 n x d x = 0 ,所以 ∫ − π π s i n ( n x ) c o s ( n x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = \int_{- \pi}^{\pi} cos (nx) sin (nx) dx =\frac {1}{2} \left [ \int_{- \pi}^{\pi} sin2nx dx + \int_{- \pi}^{\pi}sin0x dx \right] \\ & 当m=n=0时,左边变为\int_{- \pi}^{\pi} 0 dx = 0,右边计算也为0,所以 \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = 0 \\ & 当m=n \ne 0时, 左边可以看作\int_{- \pi}^{\pi} cos0x sin 2nxdx = 0,所以 \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = 0 & \end{align} ∫−ππsin(nx)cos(nx)dx=∫−ππcos(nx)sin(nx)dx=21[∫−ππsin2nxdx+∫−ππsin0xdx]当m=n=0时,左边变为∫−ππ0dx=0,右边计算也为0,所以∫−ππsin(nx)cos(nx)dx=0当m=n=0时,左边可以看作∫−ππcos0xsin2nxdx=0,所以∫−ππsin(nx)cos(nx)dx=0
总结如下:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 ∫ − π π c o s ( n x ) c o s ( m x ) d x = { 0 , m ≠ n 2 π , m = n = 0 π m = n ≠ 0 ∫ − π π s i n ( n x ) s i n ( m x ) d x = { 0 , m ≠ n 或 m = n = 0 π m = n ≠ 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = \left\{\begin{matrix} 0, & m \ne n \\ 2 \pi, & m = n =0 \\ \pi & m = n \ne 0 \end{matrix}\right.\\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = \left\{\begin{matrix} 0, & m \ne n 或 m=n=0\\ \pi & m = n \ne 0 \end{matrix}\right. & \end{align} ∫−ππsin(nx)cos(mx)dx=0∫−ππcos(nx)sin(mx)dx=0∫−ππcos(nx)cos(mx)dx=⎩ ⎨ ⎧0,2π,πm=nm=n=0m=n=0∫−ππsin(nx)sin(mx)dx={0,πm=n或m=n=0m=n=0
相关文章:

【傅里叶级数与傅里叶变换】数学推导——1、基础知识点回顾及[Part1:三角函数的正交性]介绍
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。 文章全部链接: 基础知识点 Part1:三角函数系的正交性 Part2:T2π的周期函数的傅里叶级数展开 P…...
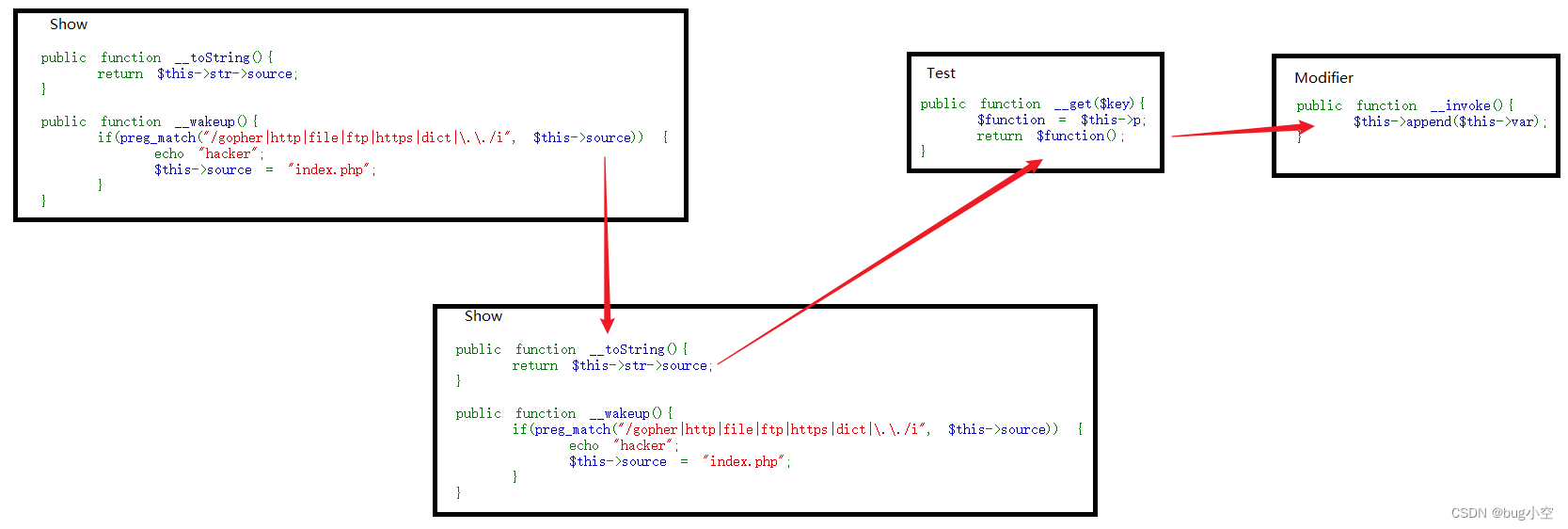
BUUCTF [MRCTF2020]Ezpop解题思路
题目代码 Welcome to index.php <?php //flag is in flag.php //WTF IS THIS? //Learn From https://ctf.ieki.xyz/library/php.html#%E5%8F%8D%E5%BA%8F%E5%88%97%E5%8C%96%E9%AD%94%E6%9C%AF%E6%96%B9%E6%B3%95 //And Crack It! class Modifier {protected $var;publi…...
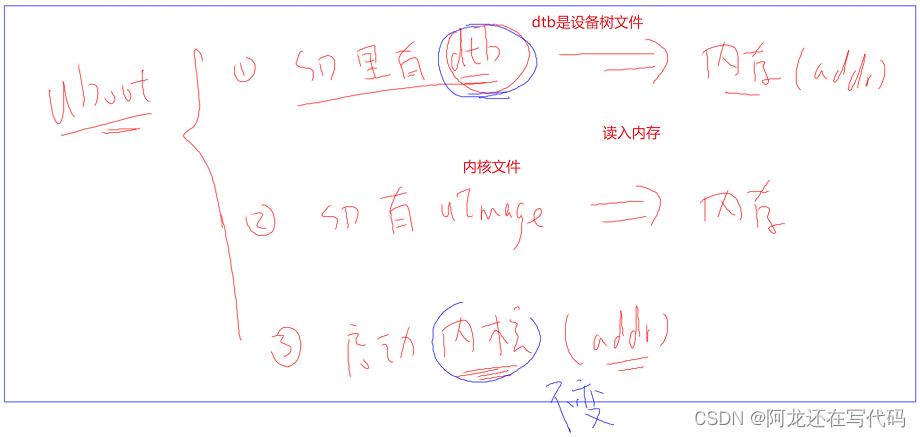
【IMX6ULL驱动开发学习】07.驱动程序分离的思想之平台总线设备驱动模型和设备树
一、驱动程序分离的思想 【IMX6ULL驱动开发学习】05.字符设备驱动开发模板(包括读写函数、poll机制、异步通知、定时器、中断、自动创建设备节点和环形缓冲区)_阿龙还在写代码的博客-CSDN博客 之前编写驱动程序的代码存在不少弊端:移植性差…...

深度学习中的python语法笔记总结
解释 torch中的 .clamp(min0) 在PyTorch中,torch.clamp将张量中的元素限制在指定的范围内。 torch.clamp(min0)会将张量中的每个元素与0进行比较,并将小于0的元素替换为0。其他大于等于0的元素则保持不变。 clamp函数原理 def clamp(x, lower, upper)…...
Reids 的整合使用
大家好 , 我是苏麟 , 今天带来强大的Redis . REmote DIctionary Server(Redis) 是一个由 Salvatore Sanfilippo 写的 key-value 存储系统,是跨平台的非关系型数据库。 Redis 是一个开源的使用 ANSI C 语言编写、遵守 BSD 协议、支持网络、可基于内存、分布式、可选…...

Vue3 —— watchEffect 高级侦听器
该文章是在学习 小满vue3 课程的随堂记录示例均采用 <script setup>,且包含 typescript 的基础用法 前言 Vue3 中新增了一种特殊的监听器 watchEffect,它的类型是: function watchEffect(effect: (onCleanup: OnCleanup) > void,o…...

Java异步子线程读取主线程参数的若干好玩场景
在开发过程中,我们难免会因为性能、实时响应等,需要异步处理的一些事务,并且在子线程中有时我们还需要获取主线程相关的参数。下面有若干方案可以实现上述场景,但会出现一定的问题。 场景1-基础场景 在主线程中开启子线程&#x…...

Android 视频开发
在 Android 平台上进行视频开发,您需要掌握以下关键知识点,以确保能够成功地开发和调试视频应用程序: Android视频架构: 了解 Android 的视频系统架构,包括视频捕获、编码、解码、渲染和显示等。 视频格式和编解码&am…...

【计算机网络篇】UDP协议
✅作者简介:大家好,我是小杨 📃个人主页:「小杨」的csdn博客 🐳希望大家多多支持🥰一起进步呀! UDP协议 1,UDP 简介 UDP(User Datagram Protocol)是一种无连…...

LeetCode 2682. 找出转圈游戏输家
【LetMeFly】2682.找出转圈游戏输家 力扣题目链接:https://leetcode.cn/problems/find-the-losers-of-the-circular-game/ n 个朋友在玩游戏。这些朋友坐成一个圈,按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i …...
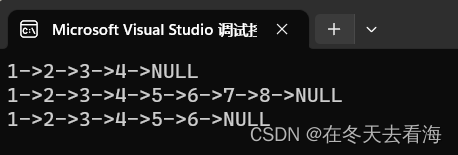
数据结构单链表
单链表 1 链表的概念及结构 概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链 接次序实现的 。 在我们开始讲链表之前,我们是写了顺序表,顺序表就是类似一个数组的东西࿰…...
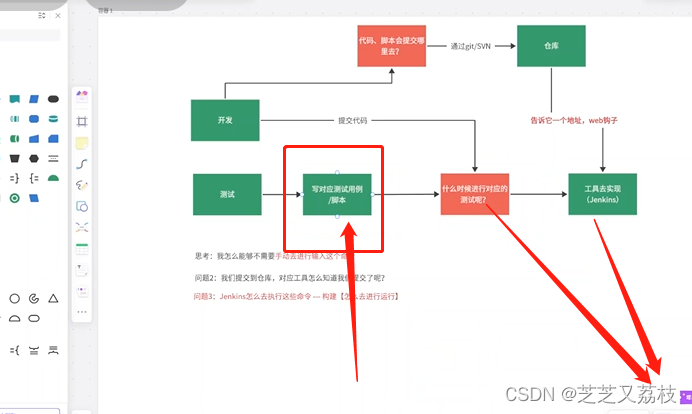
自定义WEB框架结合Jenkins实现全自动测试
自定义WEB框架结合Jenkins实现全自动测试 allure生成 allure生成 1.allure–纯命令运行 -固定的–稍微记住对应的单词即可。2 安装,2个步骤: 1.下载allure包,然后配置环境变量。 https://github.com/allure-framework/allure2/releases/tag/2.22.4 2.在…...

PHP加密与安全的最佳实践
PHP加密与安全的最佳实践 概述 在当今信息时代,数据安全是非常重要的。对于开发人员而言,掌握加密和安全的最佳实践是必不可少的。PHP作为一种常用的后端开发语言,提供了许多功能强大且易于使用的加密和安全性相关函数和类。本文将介绍一些P…...
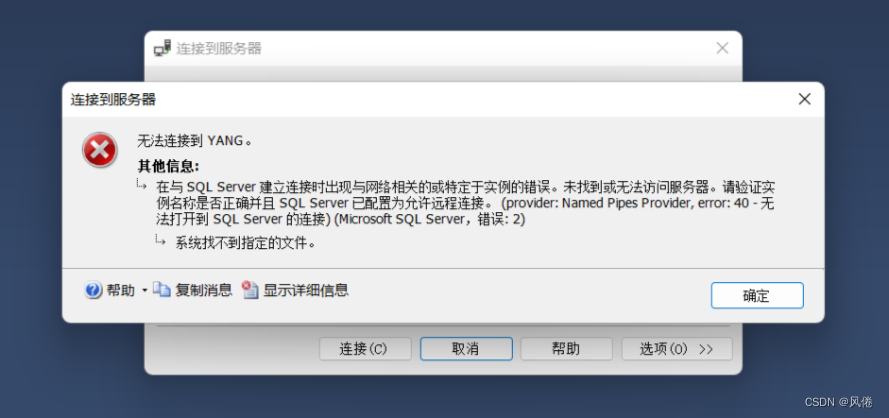
SQL Server数据库无法连接
问题如下: 原因:sql server服务器未开启 解决方法:以管理员身份打开cmd,输入:net start mssqlserver。...

videojs 播放视频
背景:在项目中使用第三方插件videojs进行播放视频,点击事件更改播放的数据源。 一、视频相关理论 (一)、背景 网络流媒体的呈现形式分为两种:直播点播 (二)、流媒体的3种协议 分类:HTTPHLSRTMP定义:基于HTTP的流媒体…...

vue强制刷新变量
在前端开发中,我们经常需要变量的值实时响应到界面上。Vue就是一个非常强大的前端框架,它的数据绑定能够非常好地实现变量与界面的同步更新。但是有时候,我们需要强制刷新某个变量的值,以便界面能及时地反映出它的变化。本文将介绍…...

[QCA6174]QCA6174 5G WiFi DFS处理逻辑分析及雷达误检率高优化规避
DFS认证信息 WIFI DFS测试要求 Master设备需要测试的项目 4.6.2.1 Channel Availability Check 信道可用性检查 定义其作为雷达脉冲检测机制,当雷达脉冲出现时所占用的信道需要能被设备检测到已经被占用。当相关信道未被占用时,这些信道被称为Avaliable Channel可用信道 …...
预防SQL漏洞注入和规避网络攻击
前言: 虽然近些年SQL注入已经被各类的安全开发框架规避了绝大部分,但SQL注入作为一种最原始的攻击手段之一,破坏力仍然十分强大,因为它直捣黄龙数据中心。所以未雨绸缪,各位不可不重视。 预防SQL注入方法措施: 服务器…...
《Go 语言第一课》课程学习笔记(一)
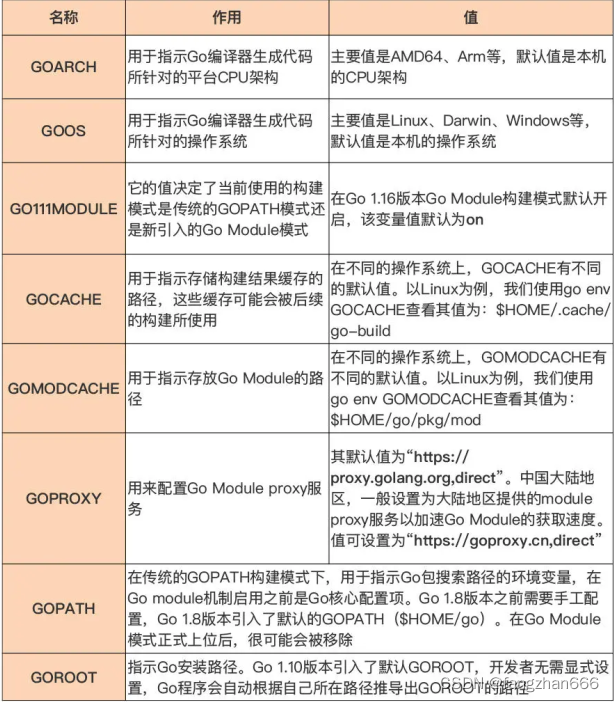
配好环境:选择一种最适合你的 Go 安装方法 选择 Go 版本 一般情况下,建议采用最新版本。因为 Go 团队发布的 Go 语言稳定版本的平均质量一直是很高的,少有影响使用的重大 bug。可以根据不同实际项目需要或开源社区的情况使用不同的版本。 有…...
网络安全 Day29-运维安全项目-iptables防火墙
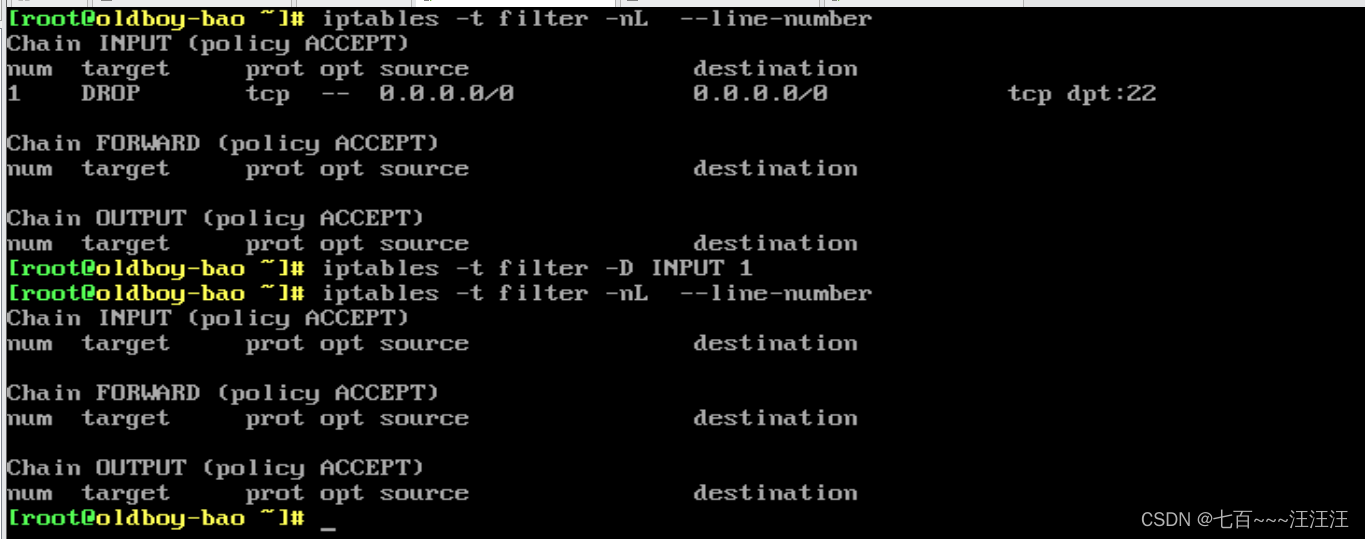
iptables防火墙 1. 防火墙概述2. 防火墙2.1 防火墙种类及使用说明2.2 必须熟悉的名词2.3 iptables 执行过程※※※※※2.4 表与链※※※※※2.4.1 简介2.4.2 每个表说明2.4.2.1 filter表 :star::star::star::star::star:2.4.2.2 nat表 2.5 环境准备及命令2.6 案例01:…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
