原码、补码、反码
一、前置概念
计算机底层存储数据时使用的是二进制数字,但是计算机在存储一个数字时并不是直接存储该数字对应的二进制数字,而是存储该数字对应二进制数字的补码。所以接下来我们需要来了解一下原码、反码和补码。
那么再了解原码、反码、补码之前,我们要了解机器数和真值的概念:
1) 机器数:
一个数在计算机的存储形式是二进制数,我们称这些二进制数为机器数,机器数是有符号,在计算机中用机器数的最高位存放符号位,0表示正数,1表示负数
2) 真值:
因为机器数带有符号位,所以机器数的形式值不等于其真实表示的值(真值),以机器数1000 0001为例,其真正表示的值(首位为符号位)为-1,而形式值(首位就是代表1)为129;因此将带符号的机器数的真正表示的值称为机器数的真值。
二、原码、反码、补码介绍
1) 原码
原码的表示与机器数真值表示的一样,即用第一位表示符号,其余位表示数值。也就是
正数:就是它对应的二进制数。
负数:将绝对值对应的二进制最左边位变为1。
例如的十进制的的正负1,用8位二进制的原码表示如下:
【+1】= 原:[ 0000 0001 ]
【-1】= 原:[ 1000 0001 ]
2) 反码
正数 : 和原码相同。
负数 : 在其原码的基础上,符号位不变,其余各位取反。
【+1】= 原: [ 0000 0001 ] = 反:[ 0000 0001 ]
【-1】 = 原:[ 1000 0001 ] = 反:[ 1111 1110 ]
3) 补码
正数 : 补码是其原码本身。
负数 : 补码是在其原码的基础上,符号位不变,其余各位取反后加1(即在反码的基础上加1)。
【+1】= 原: [ 0000 0001 ] = 反:[ 0000 0001 ] = 补:[ 0000 0001 ]
【-1】 = 原:[ 1000 0001 ] = 反:[ 1111 1110 ] = 补:[ 1111 1111 ]
三、 数据在计算机中的存储形式
计算机实际只存储补码,所以原码转换为补码的过程,也可以理解为数据存储到计算机内存中的过程:

在原、反、补码中,正数的表示是一模一样的,而负数的表示是不相同的,所以对于负数的补码来说,我们是不能直接用进制转换将其转换为十进制数值的,因为这样是得不到计算机真正存储的十进制数的,所以应该将其转换为原码后,再将转换得到的原码进行进制转换为十进制数(机器数包含符号位)
四、为何使用原码、反码、补码
我们上面说过,原码、反码、补码的表示对于正数来说都是一样的,而对于负数来说,三种码的表示确是完全不同的,那大家是否会有个疑问:如果原码才是我们人类可以识别并用于直接计算的表示方式,**那为什么还会有反码和补码?**计算机直接存储原码不就完事了?
在解决这些问题前,我们先来了解计算机的底层概念,我们人脑可以很轻松的知道机器数的第一位是符号位,但对于计算机基础电路设计来说判别第一位是符号位是非常难和复杂的事情,为了让计算机底层设计更加简单,人们开始探索将符号位参与运算,并且采用只保留加法的方法,我们知道减去一个数,等于加上这个数的负数,即:1-1 = 1 + (-1) = 0,这样让计算机运算就更加简单了,并且也让符号位参与到运算中去
五、原码、补码、反码演进的过程
提醒:前提是已经完全掌握上面的原码、反码、补码介绍
1) 使用原码运算
计算十进制表达式:1-1 = 0
1 - 1 = 1 + (-1)
= 原:[ 0000 0001 ] + 原:[ 1000 0001 ]
= 原:[ 1000 0010 ] = -2
结论:如果用原码表示,让符号位也参与计算,对于减法来说,结果是不正确的。这也是计算机内部在存储数据时不使用原码的原因,为了解决这一问题,出现了反码。
2) 使用反码运算
计算十进制表达式:1-1 = 0
1 - 1 = 1 + (-1)
= 原:[ 0000 0001 ] + 原:[ 1000 0001 ]
= 反:[ 0000 0001 ] + 反:[ 1111 1110 ]
= 反:[ 1111 1111 ] = 原: [ 1000 0000 ] = -0
结论:通过计算我们发现用反码计算减法,**结果的真值部分是正确的。**而唯一的问题出现在"0"这个特殊的数值上,虽然人们理解上+0和-0是一样的,但是0带符号是没有任何意义的,而且会有[0000 0000]原和[1000 0000]原两个编码表示0。为了解决这一问题,出现了补码。
3) 使用补码运算
1 - 1 = 1 + (-1)
= 原:[ 0000 0001 ] + 原:[ 1000 0001 ]
= 补:[ 0000 0001 ] + 补:[ 1111 1111 ]
= 补: [ 0000 0000 ] = 原: [ 0000 0000 ] = 0
结论:这样0用[0000 0000]表示,而以前出现问题的-0则不存在了,而且人们还发现可以用[1000 0000]表示-128,-128的推算过程如下:
(-1) + (-127) = -128
= 原:[1000 0001] + 原:[ 1111 1111 ]
= 补:[ 1111 1111 ] + 补:[ 1000 0001 ]
= 补:[ 1000 0000 ]
注意:因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示,只要补码是[1000 0000],其十进制数值就为-128。
4) 演进总结:
因为补码能多存储一个**-128**,而且在计算机底层中存储的是补码,所以在计算机中一个8位的二进制数的存储范围是用补码表示的**[-128,127],而不是用原码或反码表示的[-127,127]。这也可以解释为什么计算机中一个字节的取值范围是[-128,127]**。
最后也能够回答我们开始提出的问题了,原码、反码、补码的使用,是人们为了让符号位能参与运算并让计算机底层运算更加简单而设计出来的数据存储表示方式。
六、总结(牢记)
-
二进制的最高位是符号位:0表示正数,1表示负数(把 1 平放就是负号 ‘-’)。
-
正数的原码反码补码都一样,三码合一。
-
负数的反码 = 它的原码符号位不变,其它位取反。
-
负数的补码 = 它的反码 + 1, 负数的反码 = 负数的补码 - 1 。
-
0 的反码、补码都是 0 。
-
Java没有无符号数,换言之Java中的数都是有符号的。
-
在计算机运算的时候都是以 “补码” 的方式来运算的。
-
当我们看运算结果的时候,要看它的原码(重点)。
相关文章:

原码、补码、反码
一、前置概念 计算机底层存储数据时使用的是二进制数字,但是计算机在存储一个数字时并不是直接存储该数字对应的二进制数字,而是存储该数字对应二进制数字的补码。所以接下来我们需要来了解一下原码、反码和补码。 那么再了解原码、反码、补码之前&…...

煤矿调度IP语音对讲广播模块一键求助对讲矿用调度通信系统SIP语音对讲求助终端
硬件接口描述 SV-2101VP/ SV-2103VP系列网络音频模块,所有外部连接采用端子,电源采用2.0mm的端子,网络采用标准RJ45连接器,其他都是1.25mm的连接器。 端口类型定义 P ———— 电源 AI ———— 模拟输入(在这里是音…...
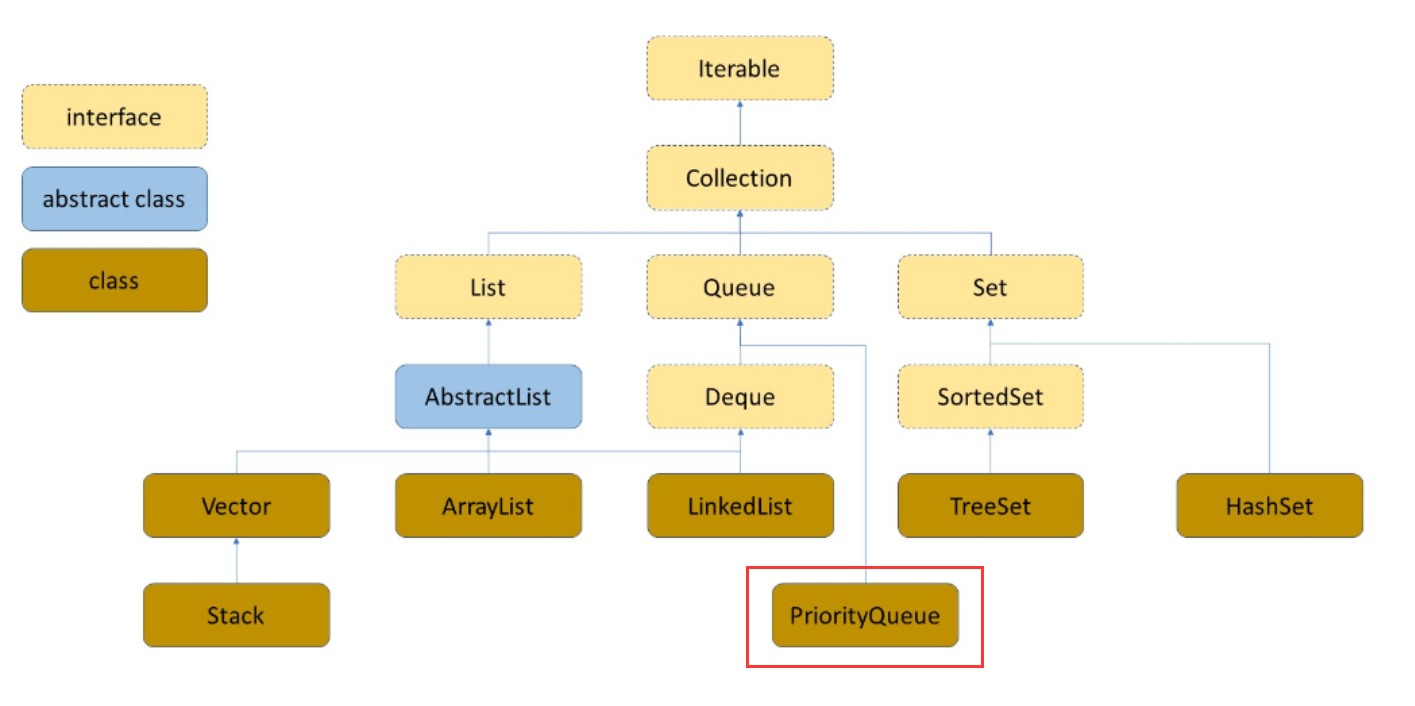
堆 和 优先级队列(超详细讲解,就怕你学不会)
优先级队列 一、堆的概念特性二、堆的创建1、向下调整算法2、向下调整建堆3、向下调整建堆的时间复杂度 三、堆的插入1、向上调整算法实现插入2、插入创建堆的时间复杂度 三、堆的删除四、Java集合中的优先级队列1、PriorityQueue 接口概述及模拟实现2、如何创建大根堆…...

AIGC绘画:基于Stable Diffusion进行AI绘图
文章目录 AIGC深度学习模型绘画系统stable diffusion简介stable diffusion应用现状在线网站云端部署本地部署Stable Diffusion AIGC深度学习模型绘画系统 stable diffusion简介 Stable Diffusion是2022年发布的深度学习文本到图像生成模型,它主要用于根据文本的描述…...

python实现对Android系统手机亮度的调节
要实现对手机亮度的调节,需要使用Android系统的API。以下是一个简单的Python代码示例,演示如何使用ADB工具和Python脚本来控制Android设备的亮度: from adb.client import Client as AdbClient import os# 连接设备 client AdbClient(host&…...
《论文阅读14》FAST-LIO
一、论文 研究领域:激光雷达惯性测距框架论文:FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter IEEE Robotics and Automation Letters, 2021 香港大学火星实验室 论文链接论文github 二、论文概…...

Kotlin CompletableDeferred 入门
在 Kotlin 中,CompletableDeferred 是一个用于异步编程的类,它提供了一种实现异步操作和等待操作结果的方式。 CompletableDeferred 是 Deferred 接口的具体实现之一,可以用于表示一个可能会在将来完成的操作。它提供了以下主要功能…...

stm32g070的PD0/PD2 PA8和PB15
目前在用STM32G070做项目,其中PD2TIMER3去模拟PWM,PD0用作按键检测,测试发现PD0低电平检测没有问题,高电平检测不到,电路图如下图所示: 用万用表测试电平,高电平1.0V左右,首先怀疑硬…...
【数据结构】 链表简介与单链表的实现
文章目录 ArrayList的缺陷链表链表的概念及结构链表的分类单向或者双向带头或者不带头循环或者非循环 单链表的实现创建单链表遍历链表得到单链表的长度查找是否包含关键字头插法尾插法任意位置插入删除第一次出现关键字为key的节点删除所有值为key的节点回收链表 总结 ArrayLi…...
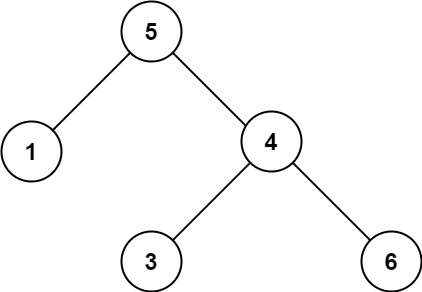
【Leetcode】98. 验证二叉搜索树
一、题目 1、题目描述 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。示例1: 输入:root = …...
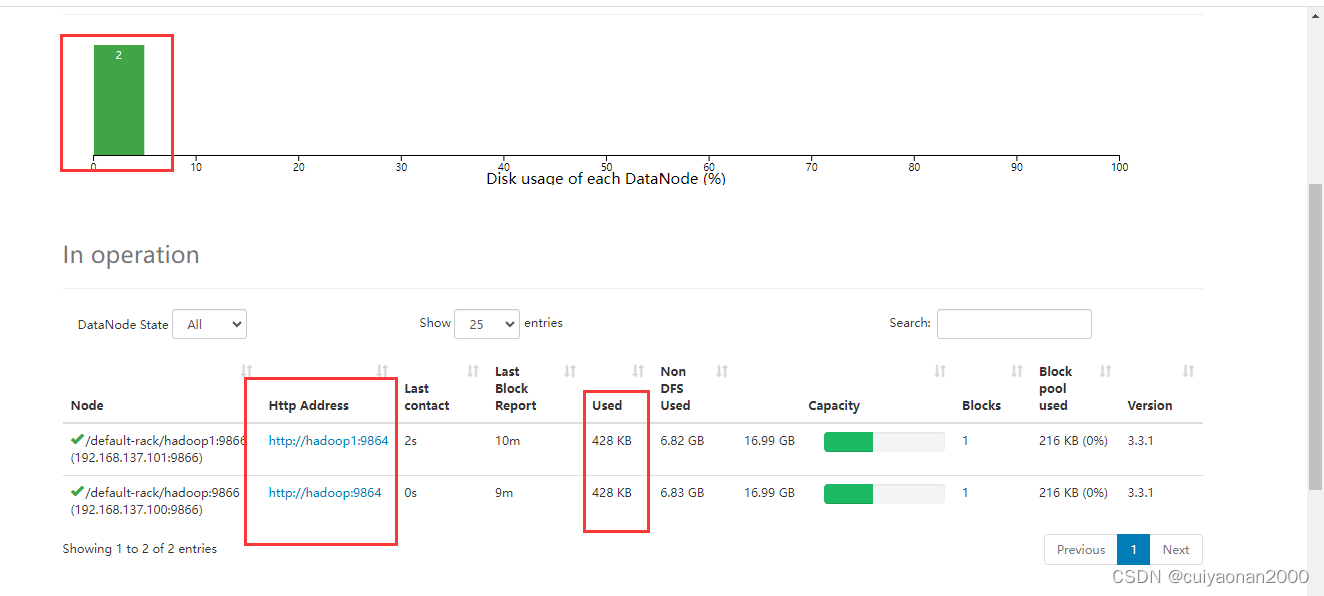
ViewFs And Federation On HDFS
序言 ViewFs 是在Federation的基础上提出的,用于通过一个HDFS路径来访问多个NameSpace,同时与ViewFs搭配的技术是client-side mount table(这个就是具体的规则配置信息可以放置在core.xml中,也可以放置在mountTable.xml中). 总的来说ViewFs的其实就是一个中间层,用于去连接不…...

每日一学——无线基础知识
无线局域网(Wireless Local Area Network,简称 WLAN)是一种使用无线通信技术连接多个无线终端设备的局域网。它通常基于无线电波传输数据,并使用无线接入点(Access Point,简称 AP)来连接无线设备…...
【腾讯云 Cloud Studio 实战训练营】在线 IDE 编写 canvas 转换黑白风格头像
关于 Cloud Studio Cloud Studio 是基于浏览器的集成式开发环境(IDE),为开发者提供了一个永不间断的云端工作站。用户在使用Cloud Studio 时无需安装,随时随地打开浏览器就能在线编程。 Cloud Studio 作为在线IDE,包含代码高亮、自动补全、Gi…...
【Hystrix技术指南】(7)故障切换的运作流程原理分析(含源码)
背景介绍 目前对于一些非核心操作,如增减库存后保存操作日志发送异步消息时(具体业务流程),一旦出现MQ服务异常时,会导致接口响应超时,因此可以考虑对非核心操作引入服务降级、服务隔离。 Hystrix说明 官方…...

Springboot 整合MQ实现延时队列入门
延时队列 添加依赖配置文件队列TTL代码架构图交换机、队列、绑定配置文件代码生产者代码消费者代码延时队列优化添加普通队列配置代码生产者发送消息是进行设置消息的ttl 通过MQ 插件实现延时队列代码架构图配置交换机生产者代码消费者代码测试发送 添加依赖 <!-- rabbitMQ …...
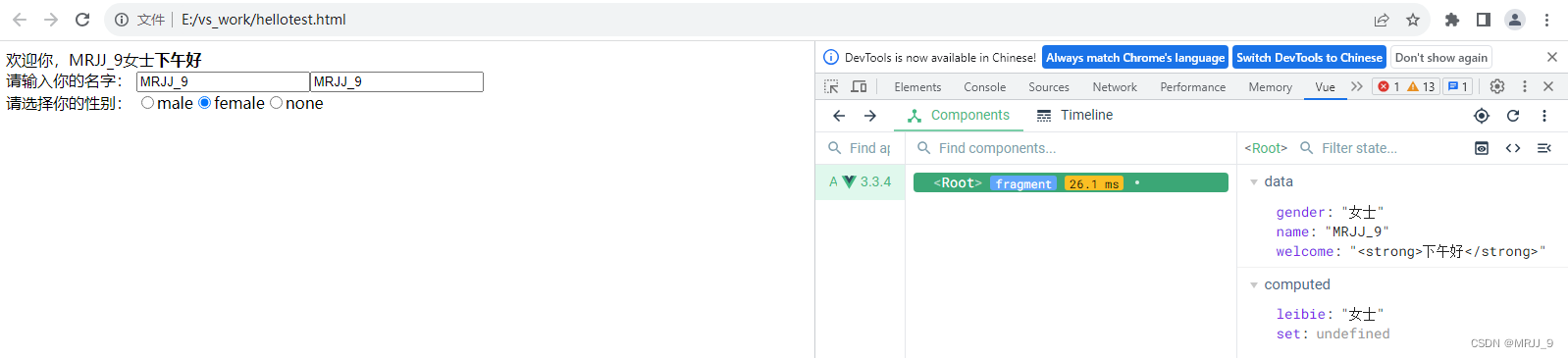
前端基础(Vue框架)
前言:前端开发框架——Vue框架学习。 准备工作:添加Vue devtools扩展工具 具体可查看下面的这篇博客 添加vue devtools扩展工具添加后F12不显示Vue图标_MRJJ_9的博客-CSDN博客 Vue官方学习文档 Vue.js - 渐进式 JavaScript 框架 | Vue.js 目录 MV…...
【实用插件】ArcGIS for AutoCAD插件分享下载
ArcGIS包含一系列功能,其中ArcGIS for AutoCAD一个免费的可下载的AutoCAD插件,它可简化将CAD和GIS数据整合在一起的过程提供互操作性。 ArcGIS for AutoCAD互操作性平台将连接AutoCAD和 ArcGIS,以增强使用地理环境设计CAD工程图时的用户体验…...
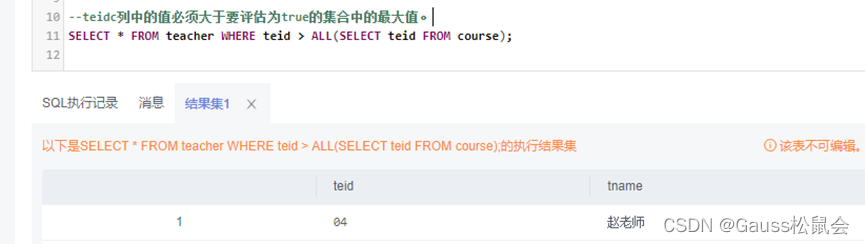
GaussDB数据库SQL系列-子查询
目录 一、前言 二、GaussDB SQL子查询表达式 1、EXISTS/NOT EXISTS 2、IN/NOT IN 3、ANY/SOME 4、ALL 三、GaussDB SQL子查询实验示例 1、创建实验表 2、EXISTS/NOT EXISTS示例 3、IN/NOT IN 示例 4、ANY/SOME 示例 5、ALL示例 四、注意事项及建议 五、小结 一、…...
Kafka 什么速度那么快
批量发送消息 Kafka 采用了批量发送消息的方式,通过将多条消息按照分区进行分组,然后每次发送一个消息集合,看似很平常的一个手段,其实它大大提升了 Kafka 的吞吐量。 消息压缩 消息压缩的目的是为了进一步减少网络传输带宽。而…...
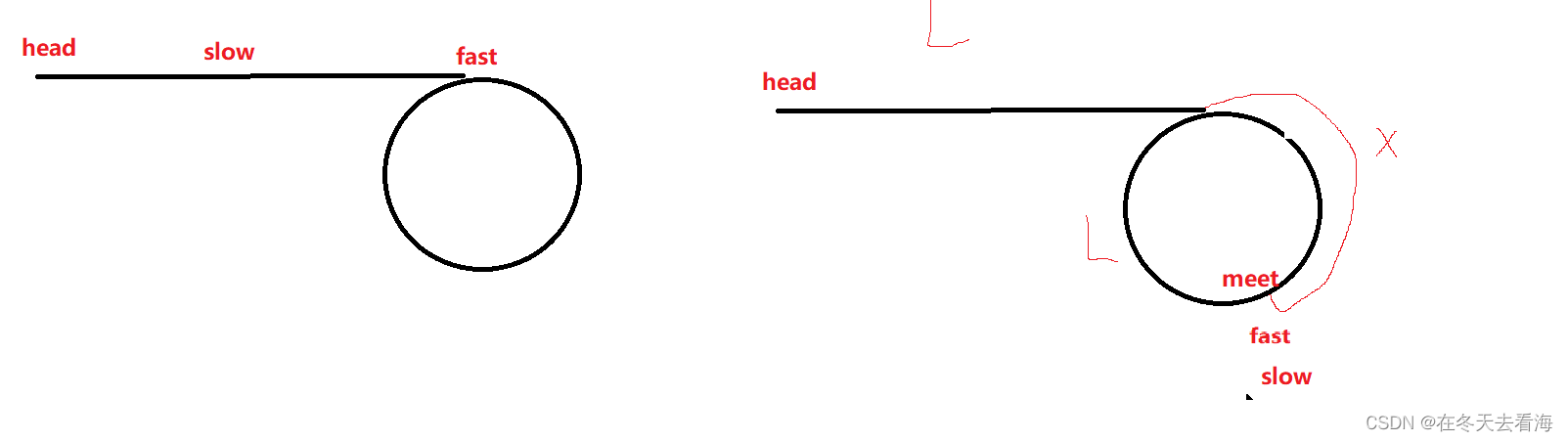
环形链表笔记(自用)
环形链表 不管怎么样slow最多走半圈了, 快慢指针slow走一步,fast走两步最合适,因为假设fast和slow相差n每一次他们前进,就会相差n-1步,这样他们一定会相遇,如果是环形链表的话。 代码 /*** Definition for…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
