Python Opencv实践 - 图像高斯滤波(高斯模糊)
import cv2 as cv
import numpy as np
import matplotlib.pyplot as pltimg = cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR)
rows,cols,channels = img.shape
print(rows,cols,channels)#为图像添加高斯噪声
#使用np.random.normal(loc=0.0, scale=1.0, size=None)
# loc: 高斯分布中心点,分布的均值
# scale: 高斯分布的宽度,分布的标准差
# size:维度。如果给定维度是(m,n,k)则从分布中抽取m*n*k个样本
#参考资料:https://blog.csdn.net/wzy628810/article/details/103807829
# https://blog.csdn.net/sinat_29957455/article/details/123977298
def AddGaussianNoise(image, mean=0, var=0.005):image = np.array(image/255, dtype=float) #将像素值归一noise = np.random.normal(mean, var ** 0.5, image.shape) #产生高斯噪声out = image + noise #直接将归一化的图片与噪声相加if out.min() < 0:low_clip = -1.else:low_clip = 0.out = np.clip(out, low_clip, 1.0)out = np.uint8(out*255)return outimg_gaussian_noise = img.copy()
gauss_mean = 0
gauss_sigma = 0.003
#增加高斯噪声到图像
img_gaussian_noise = AddGaussianNoise(img_gaussian_noise, gauss_mean, gauss_sigma)#高斯滤波(高斯模糊)
#cv.GaussianBlur(src, ksize, sigmaX, sigmaY, borderType)
#src: 输入图像
#ksize: kernel大小,高斯卷积和大小。注意卷积核的宽度和高度可以不同,但必须为正数且为奇数,也可以为零。
#sigmaX/Y: X和Y方向上的高斯标准差
#参考资料:https://blog.csdn.net/weixin_52012241/article/details/122284713
img_gaussian_blur_origin = cv.GaussianBlur(img, (3,3), 0)
img_gaussian_blur_noise = cv.GaussianBlur(img_gaussian_noise, (13,13), 0.006)#显示图像
fig,axes = plt.subplots(nrows=2, ncols=2, figsize=(10,10), dpi=100)
axes[0][0].imshow(img[:,:,::-1])
axes[0][0].set_title("Original")
axes[0][1].imshow(img_gaussian_blur_origin[:,:,::-1])
axes[0][1].set_title("Original Gaussian Blurred")
axes[1][0].imshow(img_gaussian_noise[:,:,::-1])
axes[1][0].set_title("Add Gaussian Noise")
axes[1][1].imshow(img_gaussian_blur_noise[:,:,::-1])
axes[1][1].set_title("Gaussian Noise Blurred")


相关文章:

Python Opencv实践 - 图像高斯滤波(高斯模糊)
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR) rows,cols,channels img.shape print(rows,cols,channels)#为图像添加高斯噪声 #使用np.random.normal(loc0.0, scale1.0…...

使用 Qt 生成 Word 和 PDF 文档的详细教程
系列文章目录 文章目录 系列文章目录前言一、安装 Qt二、生成 Word 文档三、生成 PDF 文档四、运行代码并查看结果五、自定义文档内容总结 前言 Qt 是一个跨平台的应用程序开发框架,除了用于创建图形界面应用程序外,还可以用来生成 Word 和 PDF 文档。本…...
ssm+vue校园美食交流系统源码
ssmvue校园美食交流系统源码和论文026 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 随着现在网络的快速发展,网上管理系统也逐渐快速发展起来,网上管理模式很快融入到了许多商…...

电力系统基础知识(一)—电力系统概述
1、电压 也称作电势差或电位差,是衡量单位电荷在静电场中由于电势不同所产生的能量差的物理量。其大小等于单位正电荷因受电场力作用从A点移动到B点所做的功,电压的方向规定为从高电位指向低电位。其单位为伏特(V,简称伏),常用单位还有千伏(kV)、毫伏(mV)、微伏(uV…...
spring(15) SpringBoot启动过程
目录 一、过程简介二、过程流程图三、源码分析1、运行 SpringApplication.run() 方法2、确定应用程序类型3、加载所有的初始化器4、加载所有的监听器5、设置程序运行的主类6、开启计时器7、将 java.awt.headless 设置为 true8、获取并启用监听器9、设置应用程序参数10、准备环境…...
耕地单目标语义分割实践——Pytorch网络过程实现理解
一、卷积操作 (一)普通卷积(Convolution) (二)空洞卷积(Atrous Convolution) 根据空洞卷积的定义,显然可以意识到空洞卷积可以提取到同一输入的不同尺度下的特征图&…...

画质提升+带宽优化,小红书音视频团队端云结合超分落地实践
随着视频业务和短视频播放规模不断增长,小红书一直致力于研究:如何在保证提升用户体验质量的同时降低视频带宽成本? 在近日结束的音视频技术大会「LiveVideoStackCon 2023」上海站中,小红书音视频架构视频图像处理算法负责人剑寒向…...
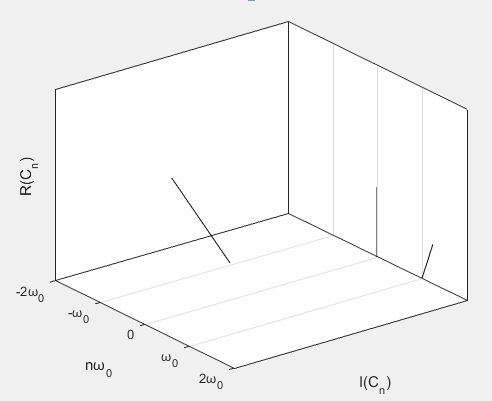
【傅里叶级数与傅里叶变换】数学推导——3、[Part4:傅里叶级数的复数形式] + [Part5:从傅里叶级数推导傅里叶变换] + 总结
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。 文章全部链接: 基础知识点 Part1:三角函数系的正交性 Part2:T2π的周期函数的傅里叶级数展开 P…...

第二章MyBatis入门程序
入门程序 创建maven程序 导入MyBatis依赖。pom.xml下导入如下依赖 <dependencies><dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId><version>3.5.6</version></dependency><dependen…...

AgentBench::AI智能体发展的潜在问题(二)
从历史上看,几乎每一种新技术的广泛应用都会在带来新机遇的同时引发很多新问题,AI智能体也不例外。从目前的发展看,AI智能体的发展可能带来的新问题可能包括如下方面: 第二是AI智能体的普及将有可能进一步加剧AI造成的技术性失业。…...
:逻辑运算符(上))
C++中的运算符总结(4):逻辑运算符(上)
C中的运算符总结(4):逻辑运算符(上) 8、逻辑运算 NOT、 AND、 OR 和 XOR 逻辑 NOT 运算用运算符!表示,用于单个操作数。表 1是逻辑 NOT 运算的真值表,这种运算将提供的布尔标记反转࿱…...
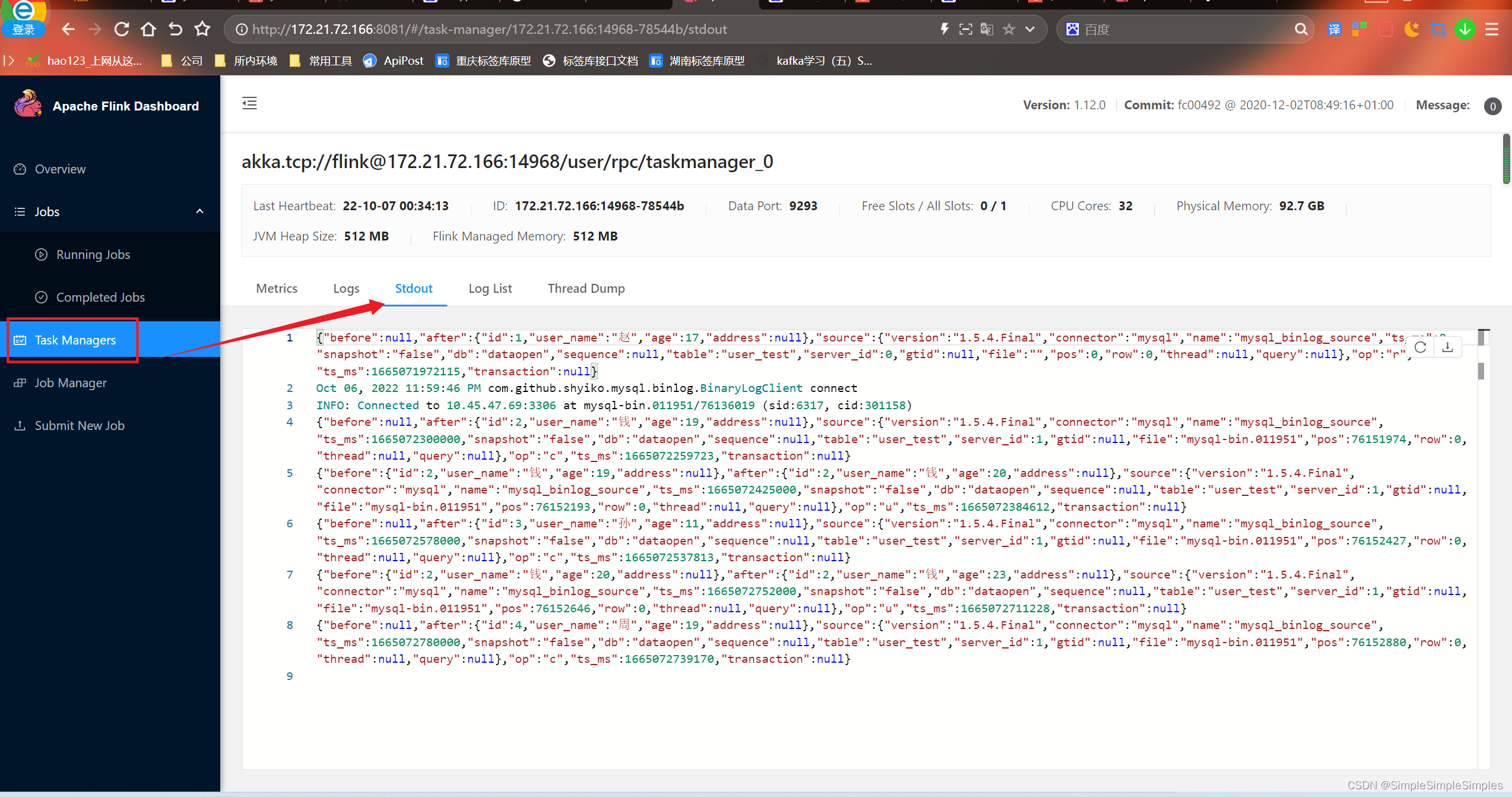
Flink安装与使用
1.安装准备工作 下载flink Apache Flink: 下载 解压 [dodahost166 bigdata]$ tar -zxvf flink-1.12.0-bin-scala_2.11.tgz 2.Flinnk的standalone模式安装 2.1修改配置文件并启动 修改,好像使用默认的就可以了 [dodahost166 conf]$ more flink-conf.yaml 启动 …...
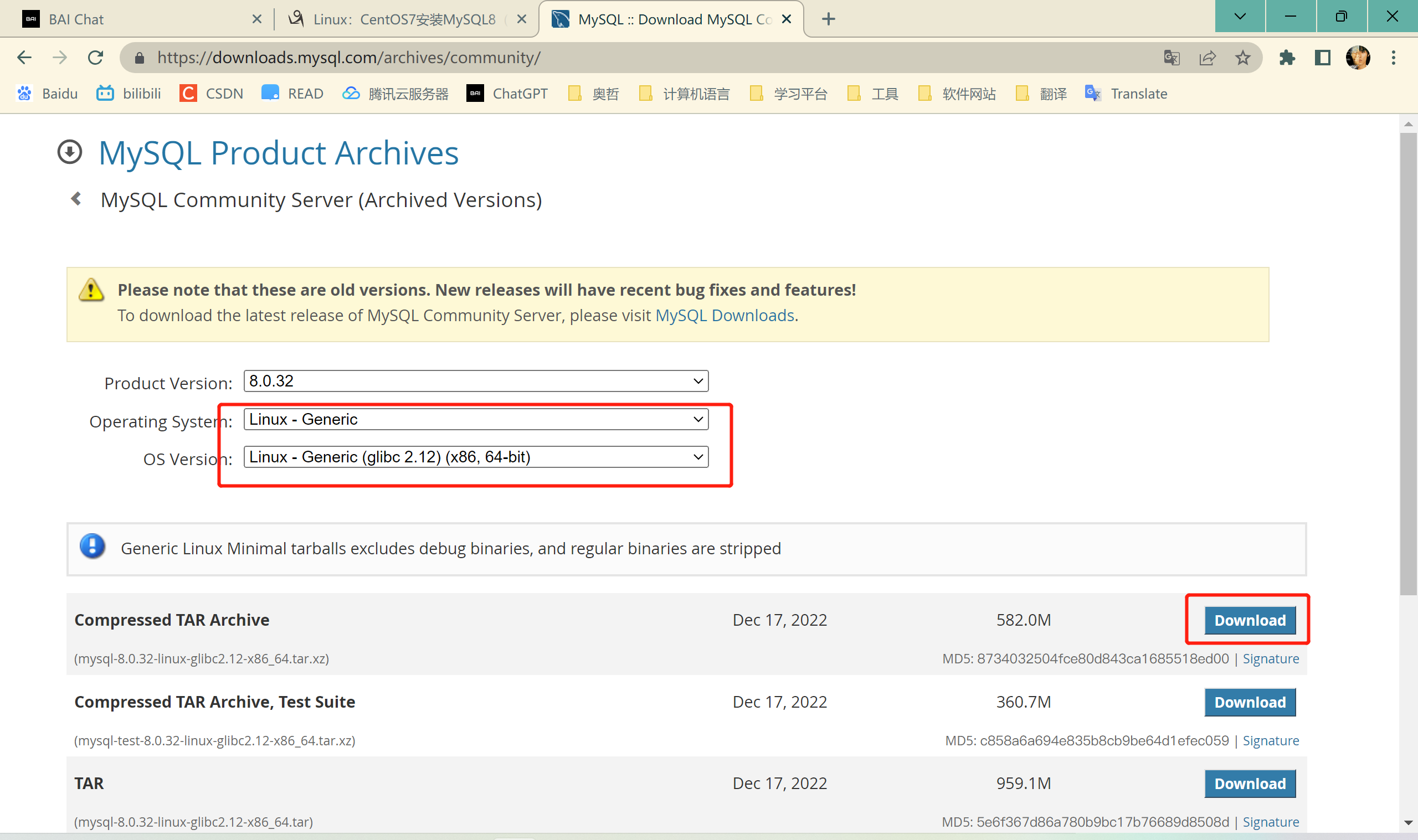
CentOS系统环境搭建(七)——Centos7安装MySQL
centos系统环境搭建专栏🔗点击跳转 坦诚地说,本文中百分之九十的内容都来自于该文章🔗Linux:CentOS7安装MySQL8(详),十分佩服大佬文章结构合理,文笔清晰,我曾经在这篇文章…...

3.react useRef使用与常见问题
react useRef使用与常见问题 文章目录 react useRef使用与常见问题1. Dom操作: useRef()2. 函数组件的转发: React.forwardRef()3. 对普通值进行记忆, 类似于一个class的实例属性4. 结合useEffect,只在更新时触发FAQ 1. Dom操作: useRef() // 1. Dom操作: useRef()let app doc…...

Axios使用CancelToken取消重复请求
处理重复请求:没有响应完成的请求,再去请求一个相同的请求,会把之前的请求取消掉 新增一个cancelRequest.js文件 import axios from "axios" const cancelTokens {}export const addPending (config) > {const requestKey …...

九耶丨阁瑞钛伦特-Spring boot与Spring cloud 之间的关系
Spring Boot和Spring Cloud是两个相互关联的项目,它们可以一起使用来构建微服务架构。 Spring Boot是一个用于简化Spring应用程序开发的框架,它提供了自动配置、快速开发的特性,使得开发人员可以更加轻松地创建独立的、生产级别的Spring应用程…...
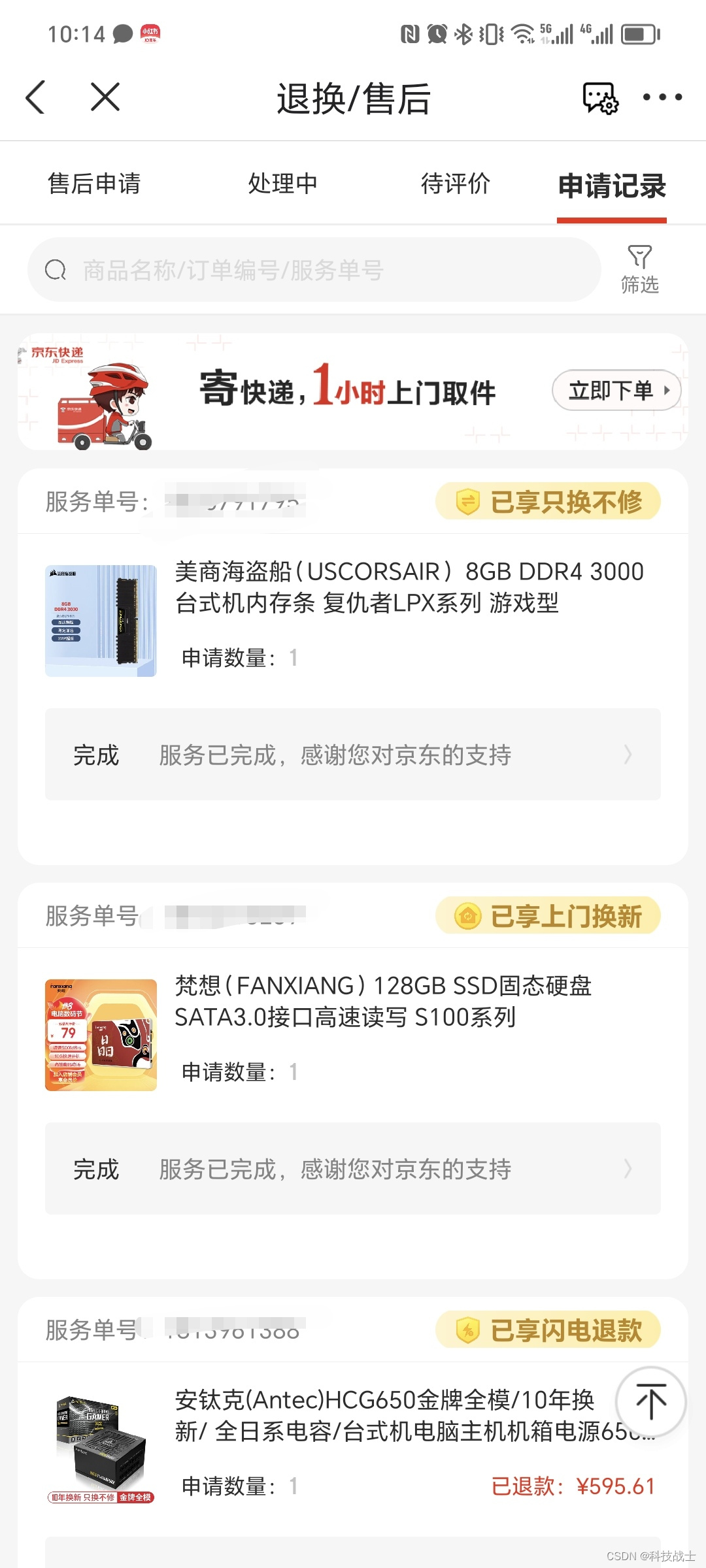
总结,由于顺丰的问题,产生了电脑近期一个月死机问题集锦
由于我搬家,我妈搞顺丰发回家,但是没有检查有没有坏,并且我自己由于不可抗力因素,超过了索赔时间,反馈给顺丰客服,说超过了造成了无法索赔的情况,现在总结发生了损坏配件有几件,显卡…...
C#程序配置读写例子 - 开源研究系列文章
今天讲讲关于C#的配置文件读写的例子。 对于应用程序的配置文件,以前都是用的ini文件进行读写的,这个与现在的json类似,都是键值对应的,这次介绍的是基于XML的序列化和反序列化的读写例子。对于ini文件,操作系统已经提…...

Angular中的管道Pipes
Angular中的管道(Pipes)是一种强大的工具,它可以处理和转换数据,然后将其呈现在视图中。它们可以被用于排序、格式化和过滤数据等任务。在本文中,我们将介绍Angular中的管道以及如何使用它们来简化开发过程。 管道的基…...
React入门 jsx学习笔记
一、JSX介绍 概念:JSX是 JavaScript XML(HTML)的缩写,表示在 JS 代码中书写 HTML 结构 作用:在React中创建HTML结构(页面UI结构) 优势: 采用类似于HTML的语法,降低学…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
