C语言好题解析(三)
目录
- 选择题一
- 选择题二
- 选择题三
- 选择题四
- 编程题一
- 编程题二
选择题一
以下程序段的输出结果是()
#include<stdio.h>
int main()
{
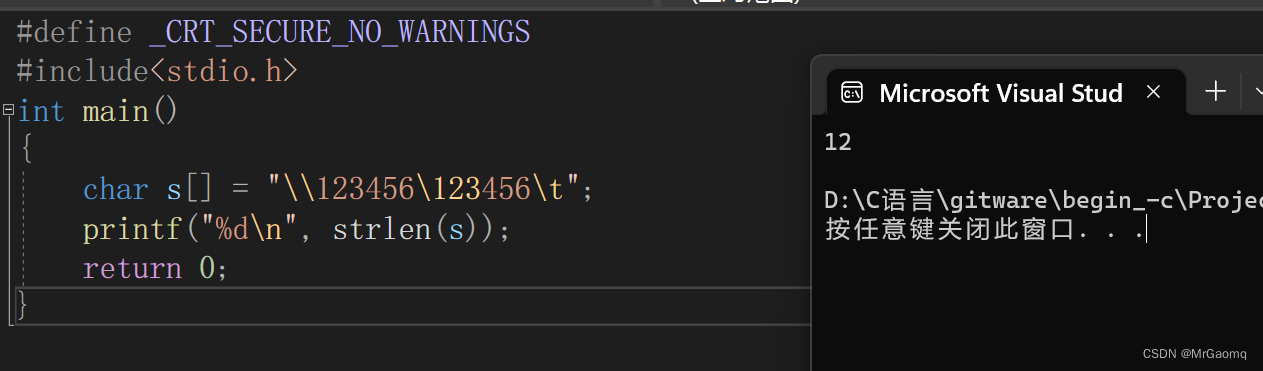
char s[] = "\\123456\123456\t";
printf("%d\n", strlen(s));
return 0;
}
A: 12 B: 13 C: 16 D: 以上都不对
【答案】 A
【分析】这道题涉及到转义字符,\是一种转义字符,而\就是以(第一个\)修饰(第二个\)使(第二个\)不表示转义的意思(这里有点绕)
因此\ \为一个字符,而123456则为6个字符。
对后面的\123456\t来说,\123表示一个字符(\ddd:ddd是表示一个1-3位的八进制数字),而456则表示3个字符,\t表示一个字符。
接下来就是strlen的含义,strlen是计算字符串的长度,直到遇见\0才会停止,因此经过前面的分析,strlen(s)=1+6+1+3+1=12
选择题二
若有以下程序,则运行后的输出结果是()
#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{
printf("%d\n", NUM);
return 0;
}
A: 4 B: 8 C: 9 D: 6
【答案】 B
【分析】这道题就是替换变量,根据上面的定义我们知道
N=2
M=N+1
NUM=(M+1)*M/2
将等式带入第三表达式即可得出结果。
值得注意的是许多人算出的结果为6,因为他们在算时NUM=(2+1+1)(2+1)/2=6(事实上这道题我也是这样算的)
但是实际上正确的算法为:
NUM=(2+1+1) *2+1/2=8.5
这是因为(M+1)*M的第二个M并没有()因此在计算时不能擅自添加()。
最后的8则是因为%d为int的打印方式,所以将小数点后的5省略了

选择题三
如下函数的 f(1) 的值为( )
int f(int n)
{
static int i = 1;
if(n >= 5)
return n;
n = n + i;
i++;
return f(n);
}
A: 5 B: 6 C: 7 D: 8
【答案】C
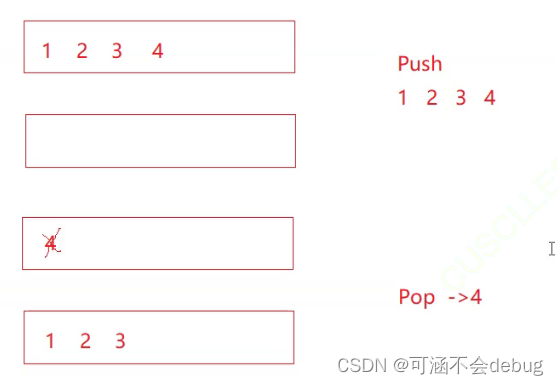
【分析】这道题是递归类型的题 ,n>=5为限制条件,但需要注意的是static修饰的i
千万不用以为int i=1,i就一直为1了,static修饰使它可以保留以前变化的值,因此i是一直在增加的
详细的过程如图:


选择题四
下面3段程序代码的效果一样吗( )
int b;
(1)const int *a = &b;
(2)int const *a = &b;
(3)int *const a = &b;
A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
【答案】 B
【分析】我们需要了解const的含义,只要了解了含义就可以做这道题
const是修饰他后面的变量使它的地址或者数值无法改变。
比如:
(1)中const修饰的是a,就说明a无法改变,因为a是表示的地址,所以a所表示的地址无法改变,但是a的值是可以改变的。
(2)中const修饰的仍是*a(和int无关)
(3)const修饰的是a,也就说明a所代表的数值无法改变,但a的地址是可以改变。
编程题一
验证尼科彻斯定理
任何一个整数 m 的立方都可以写成 m 个连续奇数之和
例如
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数 m(m≤100)
将 m 的立方写成 m 个连续奇数之和的形式输出。
注意:本题含有多组输入数据。
输入描述:输入一个int整数
输出描述:输出分解后的string
示例:
输入:6
输出:31+33+35+37+39+41
【题目分析】
我们需要用n将m的立方表示出来,然后由连续奇数之和可以设第一个奇数a1=x,然后由等差数列的求和公式可以算出Sm=m*x+(m-1)2,
即可得出关系式m^3=mx+2 * (m-1) * m
即x=m * m- m+1
因为x为第一项,为了求出x的具体值我们需要用到for循环
【代码】
int main()
{int m = 0;scanf("%d", &m);int n = m * m * m;int x = m * m - m + 1;for (int i = 1; i <= m; i++){if (i == m)printf("%d", x);else{printf("%d+", x);x += 2;}}return 0;
}
编程题二
等差数列 2,5,8,11,14, … 。(从 2 开始的 3 为公差的等差数列),求等差数列前 n 项和
注意:本题有多组输入
输入描述:输入一个正整数 n 。
输出描述:输出一个相加后的整数
示例:
输入:2 输入:275
输出:7 输出:113575
说明:2+5=7 说明:2+5+...+821+824=113575
【题目分析】
这道题和上一题的解法类似,但是是求的Sn
因此需要设一个sum(即Sn),还有x通过式子sum+=x,x+=3再加上循环即可解决问题
【代码】
#include<stdio.h>
int main()
{int n, x = 2, sum = 0;scanf("%d", &n);for (int i = 1; i <= n; i++){sum += x;x += 3;}printf("%d", sum);return 0;
}
相关文章:

C语言好题解析(三)
目录 选择题一选择题二选择题三选择题四编程题一编程题二 选择题一 以下程序段的输出结果是()#include<stdio.h> int main() { char s[] "\\123456\123456\t"; printf("%d\n", strlen(s)); return 0; }A: 12 B: 13 …...

OpenCV之remap的使用
OpenCV中使用remap实现图像的重映射。 重映射是指将图像中的某一像素值赋值到指定位置的操作:g(x,y) f ( h(x,y) ), 在这里, g( ) 是目标图像, f() 是源图像, 而h(x,y) 是作用于 (x,y) 的映射方法函数。为了完成映射过程, 需要获得一些插值为…...
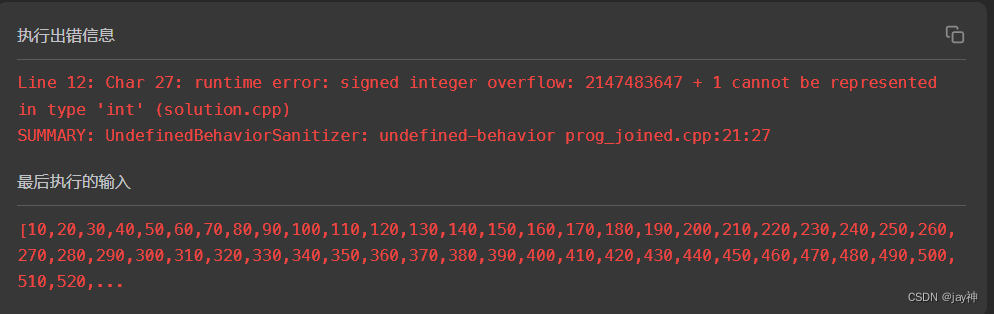
leetcode 377. 组合总和 Ⅳ
2023.8.17 本题属于完全背包问题,乍一看和昨天那题 零钱兑换II 类似,但细看题目发现:今天这题是排列问题,而“零钱兑换II”是组合问题。排列问题强调顺序,而组合顺序不强调顺序。 这里先说个结论:先遍历物品…...
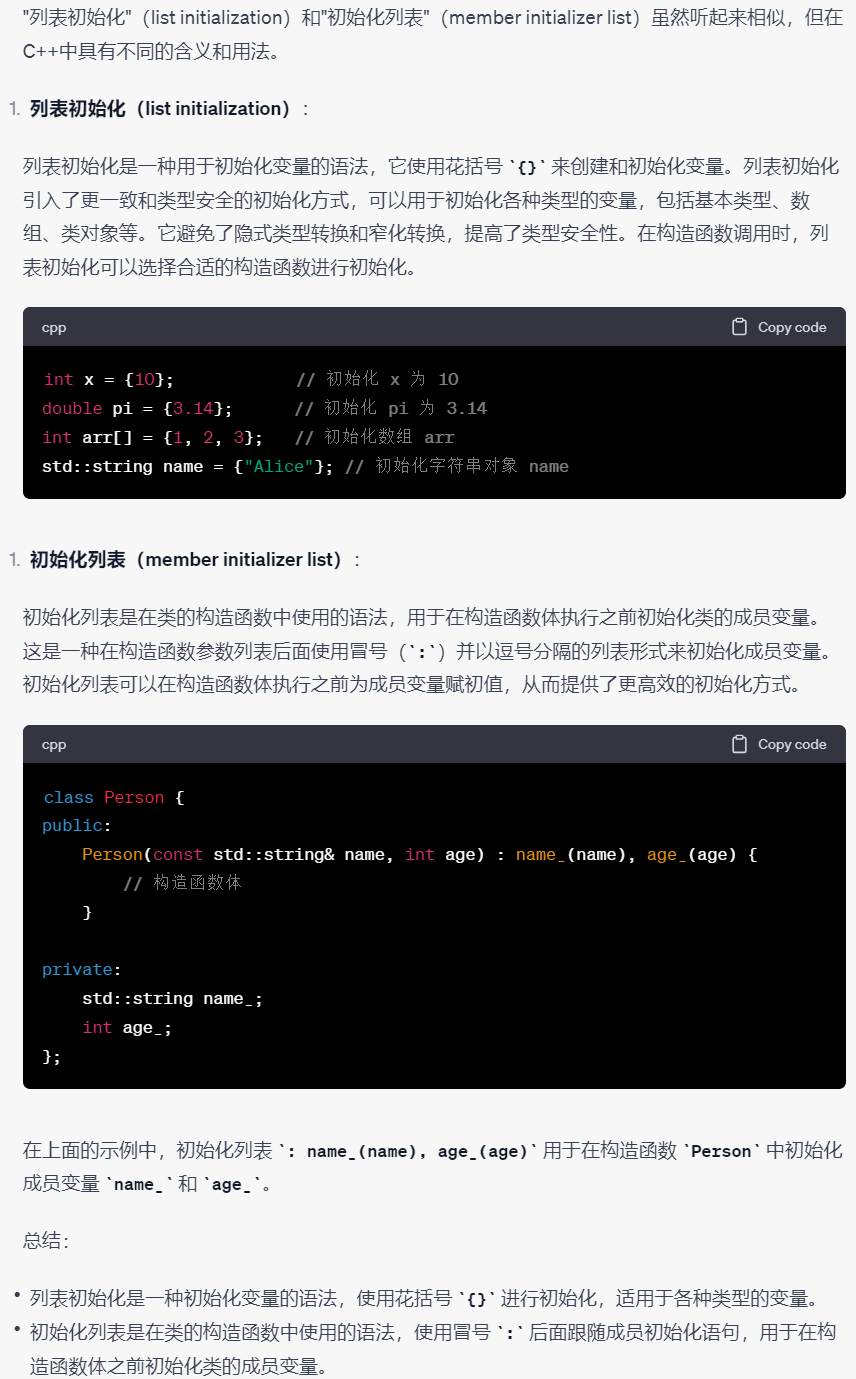
C++笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别
C笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别 code review! 文章目录 C笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别1.花括号{}进行初始化和圆括号()进行初始化2.列表初始化(list initialization࿰…...

git报错Add correct host key
想克隆备份的笔记库,失败。 测试连接github报错如下。 $ ssh -T gitgithub.comWARNING: POSSIBLE DNS SPOOFING DETECTED! The RSA host key for github.com has changed, and the key for the corresponding IP address 140.82.121.4 is unknown. This c…...
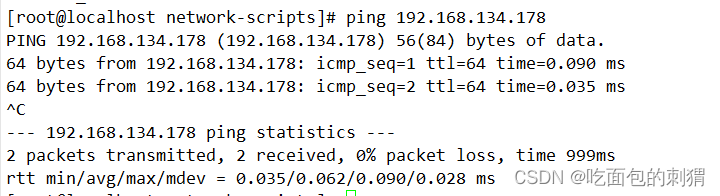
Kvm配置ovs网桥
环境:部署在kvm虚拟环境上(让虚拟机和宿主机都可以直接从路由器获取到独立ip) 1、安装ovs软件安装包并启动服务(一般采用源码安装,此处用yum安装) yum install openvswitch-2.9.0-3.el7.x86_64.rpm syste…...
AraNet:面向阿拉伯社交媒体的新深度学习工具包
阿拉伯语是互联网上第四大最常用的语言,它在社交媒体上的日益增加为大规模研究阿拉伯语在线社区提供了充足的资源。然而,目前很少有工具可以从这些数据中获得有价值的见解,用于决策、指导政策、协助应对等。这种情况即将改变吗? …...

P13-CNN学习1.3-ResNet(神之一手~)
论文地址:CVPR 2016 Open Access Repository https://arxiv.org/pdf/1512.03385.pdf Abstract 翻译 深层的神经网络越来越难以训练。我们提供了一个残差学习框架用来训练那些非常深的神经网络。我们重新定义了网络的学习方式,让网络可以直接学习输入信息与输出信息…...

【C++】set/multiset容器
1.set基本概念 #include <iostream> using namespace std;//set容器构造和赋值 #include<set>//遍历 void printSet(const set<int>& st) {for (set<int>::const_iterator it st.begin(); it ! st.end(); it){cout << *it << " …...

docker拉取镜像时报错Error response from daemon: Head ““no basic auth credentials
一:场景:新搭建一台服务器,需要拉取公司私有镜像仓库。 docker拉取私有仓库报如下错误: Error response from daemon: Head "" no basic auth credentials 二:解决方式 docker私有仓库需要登录授权,因此…...
Redis消息传递:发布订阅模式详解
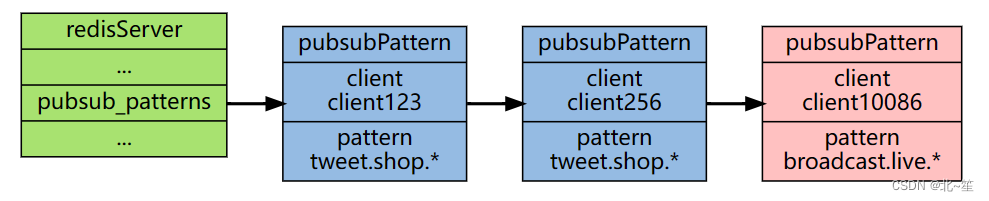
目录 1.Redis发布订阅简介 2.发布/订阅使用 2.1 基于频道(Channel)的发布/订阅 2.2 基于模式(pattern)的发布/订阅 3.深入理解Redis的订阅发布机制 3.1 基于频道(Channel)的发布/订阅如何实现的? 3.2 基于模式(Pattern)的发布/订阅如何实现的? 3.3 Sp…...
- 句柄)
最强自动化测试框架Playwright(36)- 句柄
剧作家可以为页面 DOM 元素或页面内的任何其他对象创建句柄。这些句柄存在于 Playwright 进程中,而实际对象位于浏览器中。有两种类型的句柄: JSHandle 引用页面中的任何 JavaScript 对象ElementHandle 引用页面中的 DOM 元素,它具有额外的方…...
推荐一个绘图平台(可替代Visio)
不废话,简易记网址: draw.io 网站会重定向到:https://app.diagrams.net/...

【探索Linux】—— 强大的命令行工具 P.6(调试器-gdb、项目自动化构建工具-make/Makefile)
阅读导航 前言一、什么是调试器二、详解 GDB - 调试器1.使用前提2.经常使用的命令3.使用小技巧 三、项目自动化构建工具 - make/Makefile1. make命令⭕语法⭕常用选项⭕常用操作⭕make命令的工作原理⭕make命令的优势: 2.Makefile文件⭕Makefile的基本结构⭕Makefil…...
echarts-convert.js使用
echarts-convert.js demo 点击下载 1、本地安装phantom.js插件 window版本下载 2、更改文件路径 (D:\phantomjs-2.1.1-windows\bin)改为本地项目文件路径 3、打开cmd命令行,并格式化语言 运行以下命令 将命令行语言改为中文简体 chcp…...
数据结构之队列详解(包含例题)
一、队列的概念 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操…...
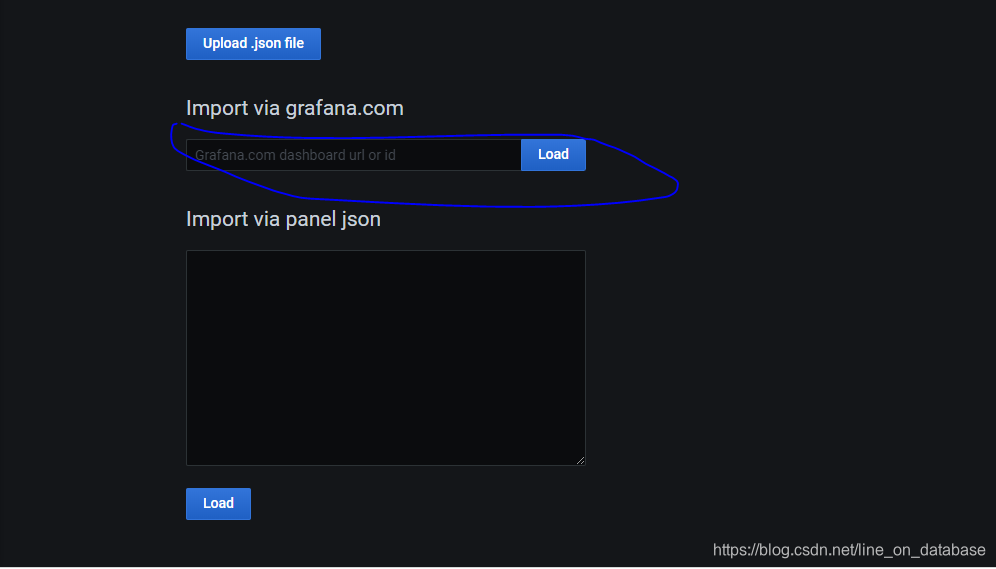
Prometheus的搭建与使用
一、安装Prometheus 官网下载地址:Download | Prometheus 解压:tar -zxvf prometheus-2.19.2.linux-amd64.tar.gz重命名: mv prometheus-2.19.2.linux-amd64 /home/prometheus进入对应目录: cd /home/prometheus查看配置文件&am…...

实战指南,SpringBoot + Mybatis 如何对接多数据源
系列文章目录 MyBatis缓存原理 Mybatis plugin 的使用及原理 MyBatisSpringboot 启动到SQL执行全流程 数据库操作不再困难,MyBatis动态Sql标签解析 从零开始,手把手教你搭建Spring Boot后台工程并说明 Spring框架与SpringBoot的关联与区别 Spring监听器…...
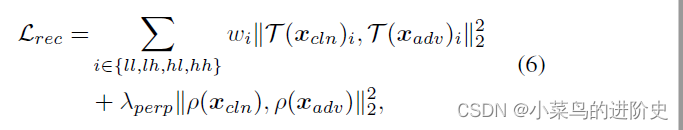
论文阅读——Imperceptible Adversarial Attack via Invertible Neural Networks
Imperceptible Adversarial Attack via Invertible Neural Networks 作者:Zihan Chen, Ziyue Wang, Junjie Huang*, Wentao Zhao, Xiao Liu, Dejian Guan 解决的问题:虽然视觉不可感知性是对抗性示例的理想特性,但传统的对抗性攻击仍然会产…...
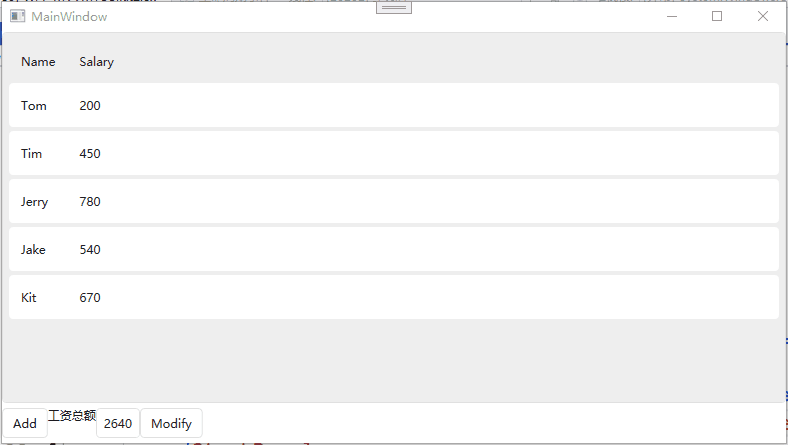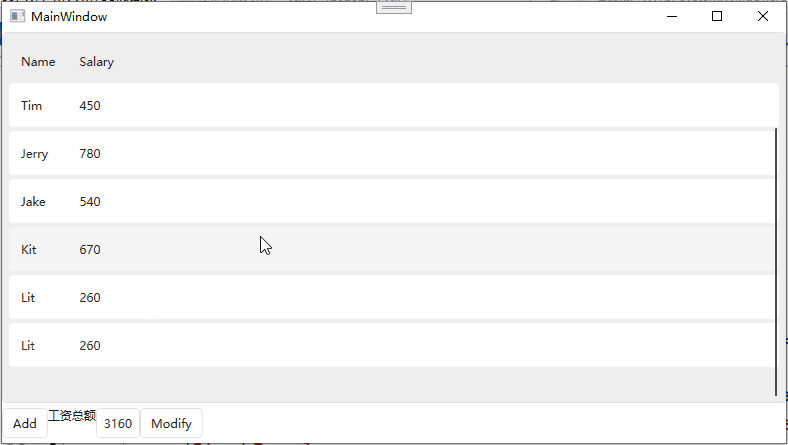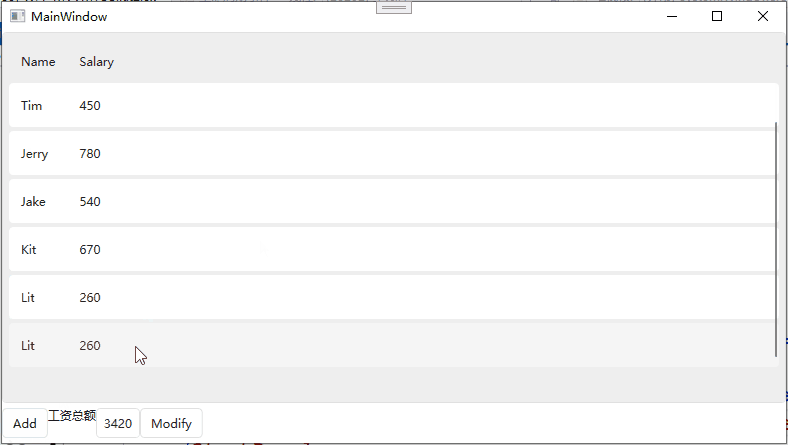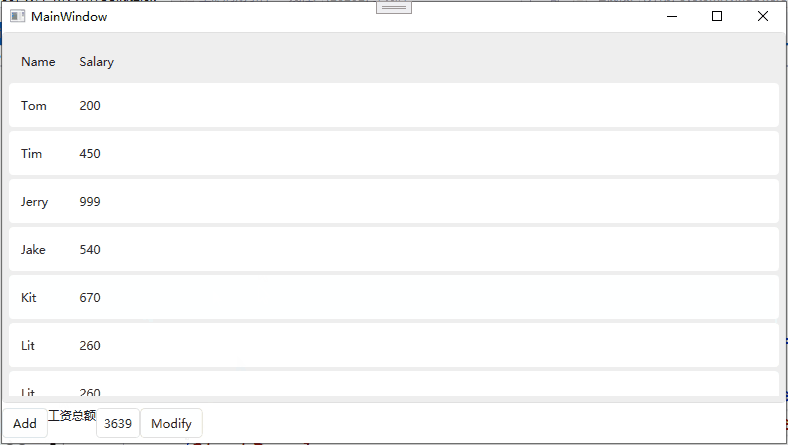
List和ObservableCollection和ListBinding在MVVM模式下的对比
List和ObservableCollection和ListBinding在MVVM模式下的对比 List 当对List进行增删操作后,并不会对View进行通知。 //Employee public class Employee : INotifyPropertyChanged {public event PropertyChangedEventHandler? PropertyChanged;public string N…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
