电子技术——共栅和共源共栅放大器的高频响应
电子技术——共栅和共源共栅放大器的高频响应

我们在之前学过无论是是CS放大器还是CE放大器,都可以看做是一个带通(IC低通)滤波器。在高频处的响应收到输入电容 CinC_{in}Cin 的限制(主要是米勒效应)。因此,若想扩大放大器的带宽,我们必须减小米勒效应,一种方案就是共栅放大器。
CG放大器的高频响应
下图展示了CG放大器的高频模型:
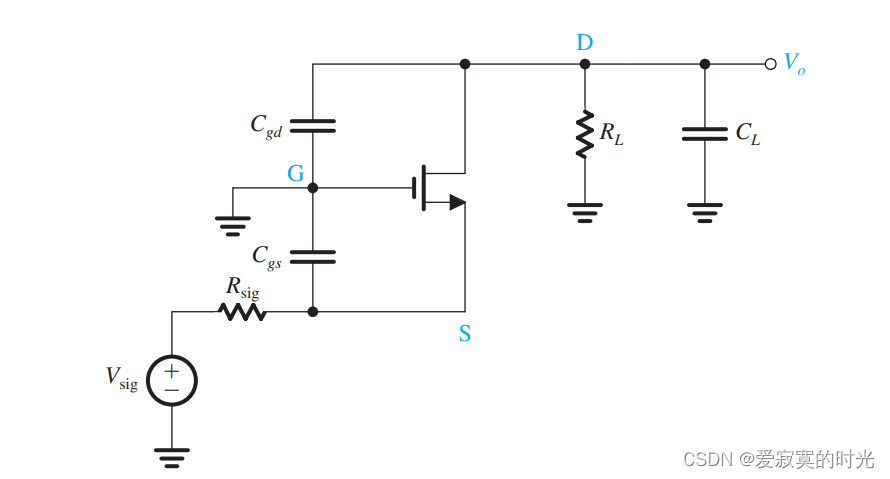
为了一般性,我们在输出端引入了电容 CLC_LCL 表示负载电容,我们发现在CG配置中,我们发现 CgdC_{gd}Cgd 和 CLC_LCL 是并联关系,在以后的分析中我们将其捏合在一起分析。
我们发现上面三个电容,每一个电容的一端都和地相连,因此每一个电容都不是桥路电容,因此不受米勒效应的影响。这说明,CG放大器的带宽要比CS放大器的带宽要宽很多,尤其是输入源阻抗很大的时候。为了分析其高频响应,我们使用T模型分析:
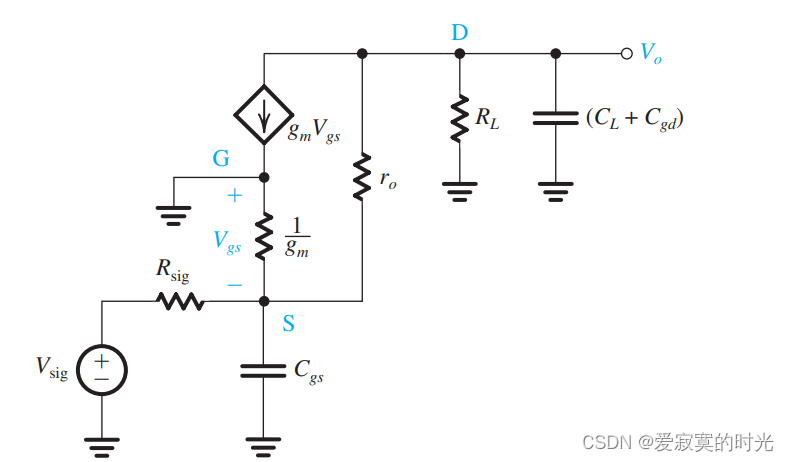
其中,为了方便分析,我们忽略 ror_oro :
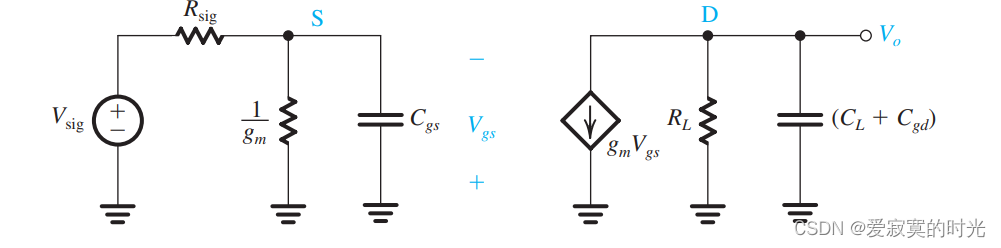
我们知道这个电路应该存在两个极点,对于输入端的低通型STC:
fP1=12πCgs(Rsig∣∣1gm)f_{P1} = \frac{1}{2 \pi C_{gs}(R_{sig}||\frac{1}{g_m})} fP1=2πCgs(Rsig∣∣gm1)1
对于输出端的低通型STC:
fP2=12π(Cgd+CL)RLf_{P2} = \frac{1}{2 \pi (C_{gd} + C_L)R_L} fP2=2π(Cgd+CL)RL1
通常情况下 fP2f_{P2}fP2 要比 fP1f_{P1}fP1 小,因此 fP2f_{P2}fP2 为主导极点。无论怎样说,两个极点都要比CS的极点大,因此CG放大器的具有更大的带宽。
或者,我们可以使用开路时间常数法得到:
fH=12πτH=1/(1fP1+1fP2)f_H = \frac{1}{2 \pi \tau_H} = 1 / (\frac{1}{f_{P1}} + \frac{1}{f_{P2}}) fH=2πτH1=1/(fP11+fP21)
在IC中,必须考虑 ror_oro ,此时我们使用开路时间常数法,首先考虑 CgsC_{gs}Cgs :

得到:
Rgs=Rsig∣∣RinR_{gs} = R_{sig} || R_{in} Rgs=Rsig∣∣Rin
这里的 RinR_{in}Rin 是CG放大器的输入阻抗。
接下来考虑电容 CgdC_{gd}Cgd :
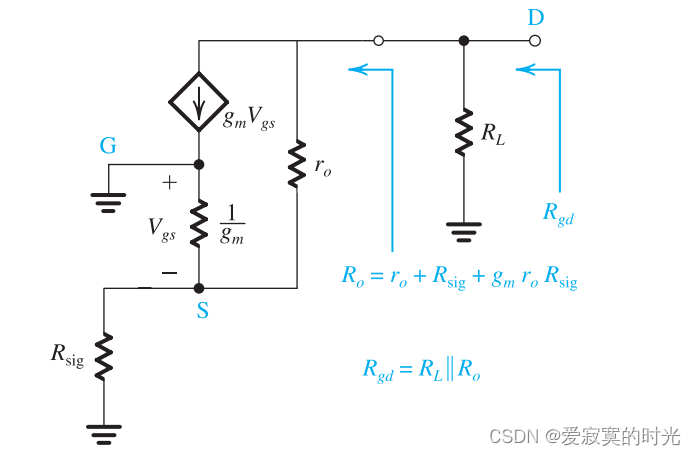
得到:
Rgd=RL∣∣RoR_{gd} = R_L || R_o Rgd=RL∣∣Ro
这里 RoR_oRo 是放大器的输出阻抗(包括 RsigR_{sig}Rsig )。
最后计算 fHf_HfH 即可。
总之,CG放大器的高频响应要比CS放大器优秀,但是由于CG放大器的低输入阻抗,导致整体增益较小。然而,CG可以和CS放大器一起工作,组成共源共栅放大器。
共源共栅放大器的高频响应
下图展示了共源共栅放大器的高频响应模型:
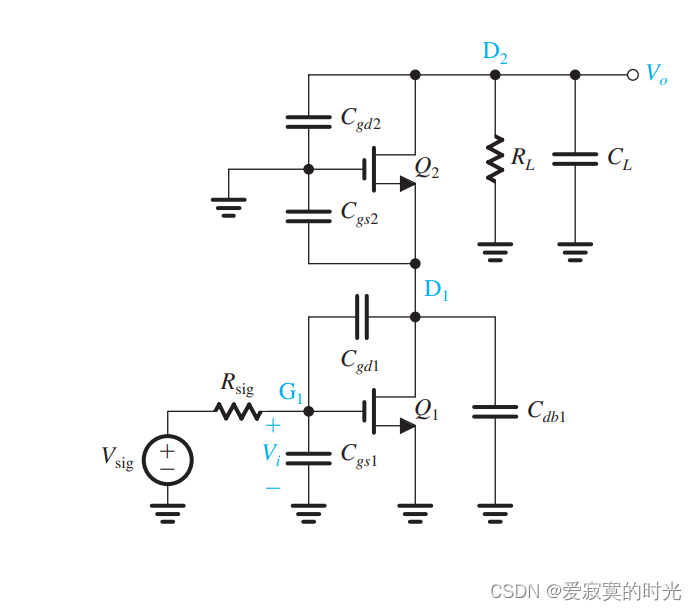
为了估算共源共栅放大器的 fHf_HfH 我们使用开路时间常数法:
- 考虑电容 Cgs1C_{gs1}Cgs1 看到的电阻为 RsigR_{sig}Rsig
- 考虑电容 Cgd1C_{gd1}Cgd1 看到的电容为 Rgd1=(1+gm1Rd1)Rsig+Rd1R_{gd1} = (1 + g_{m1}R_{d1})R_{sig} + R_{d1}Rgd1=(1+gm1Rd1)Rsig+Rd1 其中 Rd1R_{d1}Rd1 是 D1D_1D1 对地的电阻等于 Rd1=ro1∣∣Rin2=ro1∣∣ro2+RLgm2ro2R_{d1} = r_{o1} || R_{in2} = r_{o1} || \frac{r_{o2} + R_L}{g_{m2} r_{o2}}Rd1=ro1∣∣Rin2=ro1∣∣gm2ro2ro2+RL
- 考虑电容 Cdb1C_{db1}Cdb1 和 Cgs2C_{gs2}Cgs2 看到的电阻为 Rd1R_{d1}Rd1
- 考虑电容 CL+Cgd2C_L + C_{gd2}CL+Cgd2 看到的电阻为 RL∣∣RoR_L || R_oRL∣∣Ro 其中 RoR_oRo 是共源共栅放大器的输出电阻 Ro=ro2+ro1+gm2ro2ro1R_o = r_{o2} + r_{o1} + g_{m2}r_{o2}r_{o1}Ro=ro2+ro1+gm2ro2ro1
计算 fHf_HfH 即可。
权衡带宽和增益
为了说明如何权衡带宽和增益,我们观察总体时间常数:
τH=Rsig[Cgs1+Cgd1(1+gm1Rd1)]+Rd1(Cgd1+Cdb1+Cgs2)+(RL∣∣Ro)(CL+Cgd2)\tau_H = R_{sig}[C_{gs1} + C_{gd1}(1 + g_{m1}R_{d1})] + R_{d1}(C_{gd1} + C_{db1} + C_{gs2}) + (R_L || R_o)(C_L + C_{gd2}) τH=Rsig[Cgs1+Cgd1(1+gm1Rd1)]+Rd1(Cgd1+Cdb1+Cgs2)+(RL∣∣Ro)(CL+Cgd2)
首先第一项由共栅放大器的米勒效应贡献,若信号源的内阻较大,此时高频响应由第一项主导。此时想要增加放大器的带宽,我们可以降低负载阻抗 RLR_LRL 进而降低 Rd1R_{d1}Rd1 减小米勒效应。但是若将 RLR_LRL 降低我们知道电压增益也会随之降低。
当 RsigR_{sig}Rsig 较小的时候,第一项的米勒效应就不再是主导因素。此时可以使用较大的 RLR_LRL 来增大电压增益。此时第三项将是主导项,为了进一步说明,我们假设 Rsig=0R_{sig} = 0Rsig=0 并且忽略第二项:
τH≃(CL+Cgd2)(RL∣∣Ro)\tau_H \simeq (C_L + C_{gd2})(R_L || R_o) τH≃(CL+Cgd2)(RL∣∣Ro)
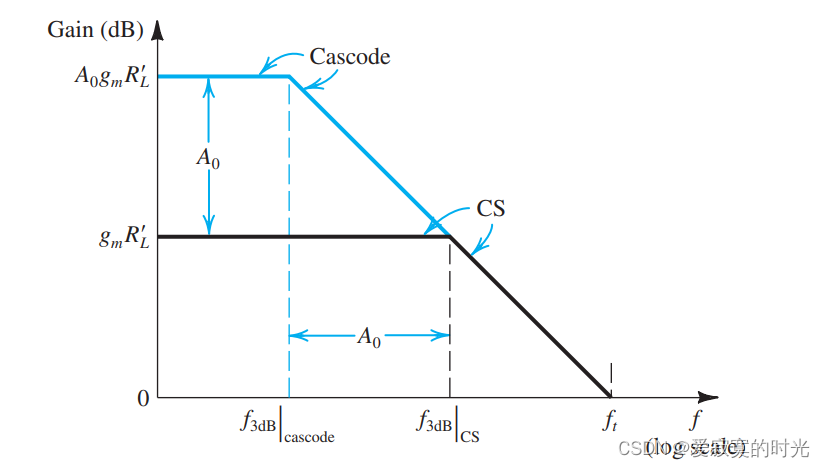
到这里我们就可以和CS放大器比较,如下图:

上图中,我们假设共源共栅放大器中 RL=A0RLR_L = A_0R_LRL=A0RL 我们发现共源共栅放大器的电压增益比CS放大器的大 A0A_0A0 倍,但是 f3dBf_{3dB}f3dB 比 CS放大器小 A0A_0A0 倍。但是单位增益不变。如图:
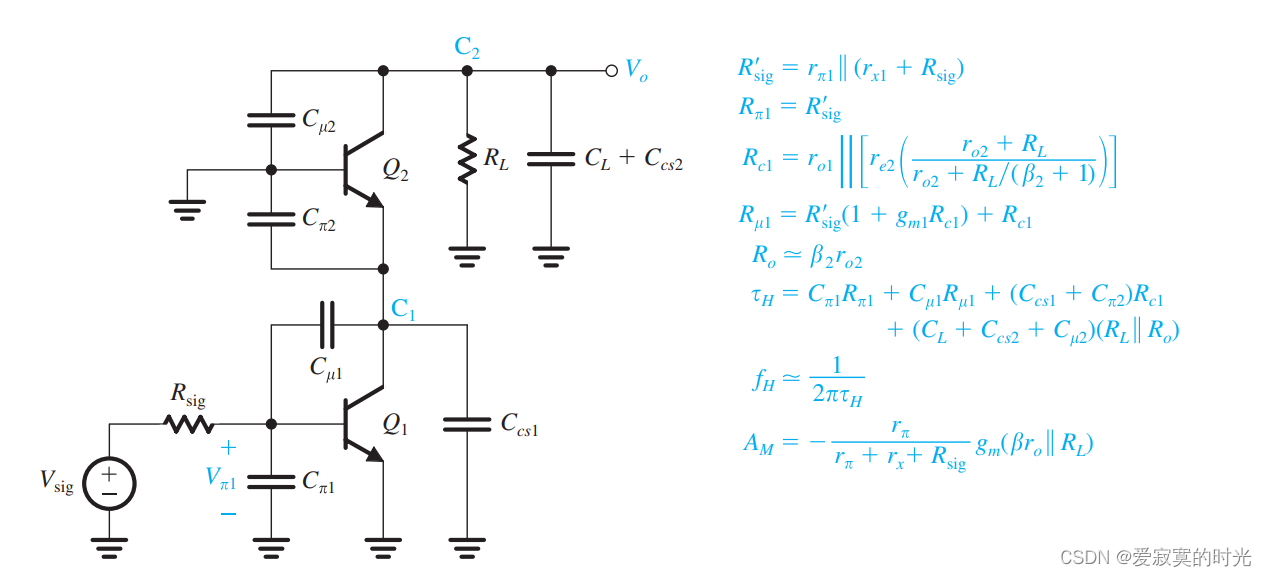
BJT共射共基放大器的高频响应
BJT共射共基放大器的高频响应与MOS的基本一致,如图:
相关文章:

电子技术——共栅和共源共栅放大器的高频响应
电子技术——共栅和共源共栅放大器的高频响应 我们在之前学过无论是是CS放大器还是CE放大器,都可以看做是一个带通(IC低通)滤波器。在高频处的响应收到输入电容 CinC_{in}Cin 的限制(主要是米勒效应)。因此ÿ…...

基于jsplumb构建的流程设计器
项目背景 最近在准备开发工作流引擎相关模块,完成表结构设计后开始着手流程设计器的技术选型,调研了众多开源项目后决定基于jsplumb.js开源库进行自研开发,保证定制化的便捷性,相关效果图及项目地址如下 项目地址:ht…...

解析从Linux零拷贝深入了解Linux-I/O(下)
接上文解析从Linux零拷贝深入了解Linux-I/O(上) 大文件传输场景 零拷贝还是最优选吗 在大文件传输的场景下,零拷贝技术并不是最优选择;因为在零拷贝的任何一种实现中,都会有「DMA 将数据从磁盘拷贝到内核缓存区——P…...

【学习笔记2.19】动态规划、MySQL、Linux、Redis(框架)
动态规划 343整数拆分 class Solution {public int integerBreak(int n) {int dp [] new int [n 1];//dp[i]:正整数i拆分后的最大乘积dp[2] 1;for(int i 2;i < n ;i ){for(int j 1;j < i;j ){dp[i] Math.max(dp[i],Math.max(j * (i - j),j * dp[i - j]));} …...
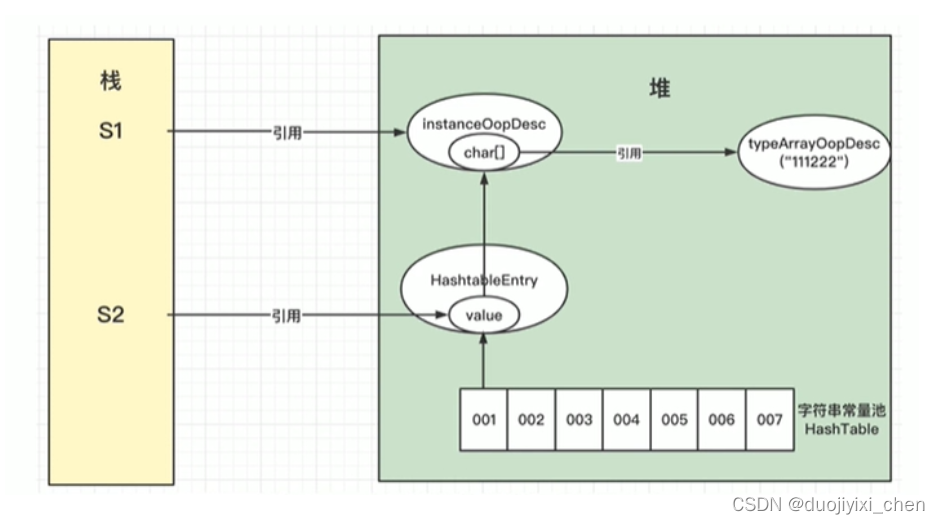
String intern方法理解
1、原理 参考学习视频: https://www.bilibili.com/video/BV1WK4y1M77t/?spm_id_from333.337.search-card.all.click&vd_source4dc3f886f5ce1d43363b603935f02bd1 String s1 “hello”; String s1 "hello"; 代码原理解释如下图String s1 new Str…...

解决 cocosjs与安卓原生集成 崩溃问题
版本:cocos2dx3.16 背景:公司需要把游戏整合到一个APP里面。于是打算通过activity切换的方式实现。但是游戏退出重进之后总会出现fatal 11线程报错。于是有了以下修改。我是底层小白。折腾了好久总算鼓捣出一个能用的版本。优化的地方应该有很多。不过就没去好好优…...
spring注解方式整合Dubbo
系列文章目录 文章目录系列文章目录一、创建一个父工程项目二、创建子模块(dubbo-api模块)二、创建子模块(dubbo-provider模块)三、创建子模块(dubbo-consumer模块)总结一、创建一个父工程项目 这里我们通过Spring Initializer 来帮我们构建一个spring-dubbo这个父项目,点击nex…...
Git详解
Git1.Git简介1.1 Git是什么1.2 Git的作用1.3 Git的简介1.4 Git的下载和安装1.5 Git的安装目录结构如下2.Git代码托管服务2.1 常用的Git代码托管服务1.Git简介 1.1 Git是什么 Git是一个分布式版本控制工具,主要用于管理开发过程中的源代码文件(Java类、x…...

003__JAVA模板方法-设计模式
模板方法 定义:定义了一个算法的骨架,并允许子类为一个或多个步骤提供实现 举个例子,把大象放进冰箱分几步,第一打开冰箱,第二打大象放进冰箱,第三把冰箱关闭。这三个步骤就可以用模板方法的设计模式。 …...

Springboot项目集成Netty组件
系列文章目录 Springboot项目集成Netty组件 Netty新增解析数据包指定长度功能 文章目录系列文章目录前言一、Netty是什么?二、使用步骤1. 项目引入依赖1.1 项目基础版本信息:1.2 Netty依赖2. 项目配置2.1 在 yml 配置文件中配置以下:2.2 创建…...

python 中的import cfg问题
pip install cfg 报错: ERROR: Could not find a version that satisfies the requirement cfg (from versions: none) ERROR: No matching distribution found for cfg 要使用pip install cfg2才行...
[oeasy]python0088_字节_Byte_存储单位_KB_MB_GB_TB
编码进化 回忆上次内容 上次 回顾了 字符大战的结果 ibm 曾经的 EBCDIC 由于字符不连续的隐患 导致后续 出现 无数问题无法补救 7-bit 的 ASA X3.4-1963 字母序号连续 比较字符时 效率高判断字符 是否是字母 也很容易 获得了 IBM以外公司的 支持 为什么 ASA X3.4-1963 是 7…...
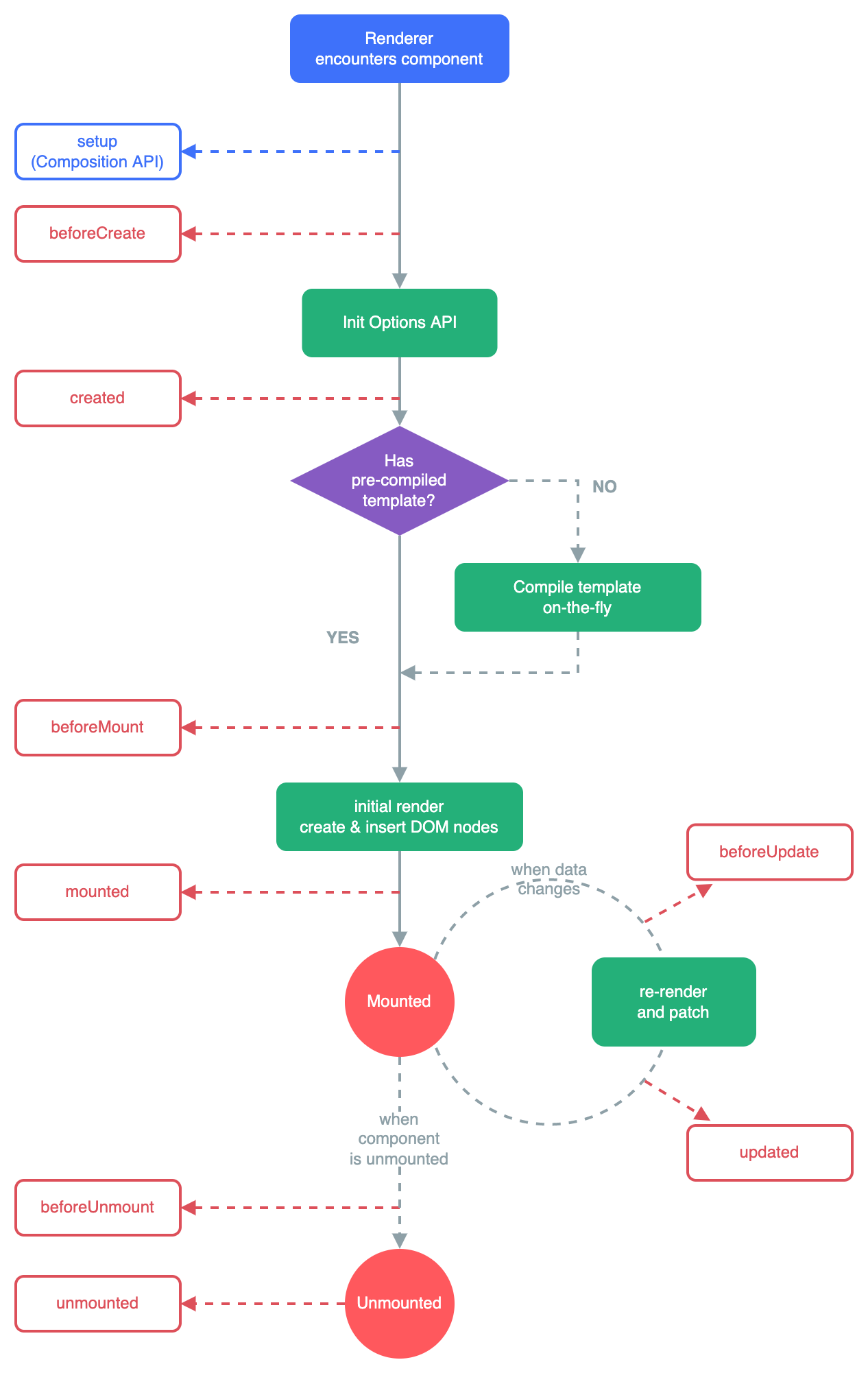
vue3.0 生命周期
目录前言:vue3.0生命周期图例1.beforeCreate2.created3.beforeMount/onBeforeMount4.mounted/onMounted5.beforeUpdate/onBeforeUpdate6.updated/onUpdated7.beforeUnmount/onBeforeUnmount8.unmounted/onUnmounted案例:总结前言: 每个Vue组…...

CGAL 数字类型
文章目录 一、简介二、内置数字类型三、CGAL中的数字类型参考资料一、简介 在CGAL汇总,数字类型必须满足特定的语法和语义要求,这样它们才能在CGAL代码中成功使用。一般来说,它们往往是代数结构概念的模型,如果它们对实数的子集模型,那么它们就也是RealEmbeddable模型。 二…...
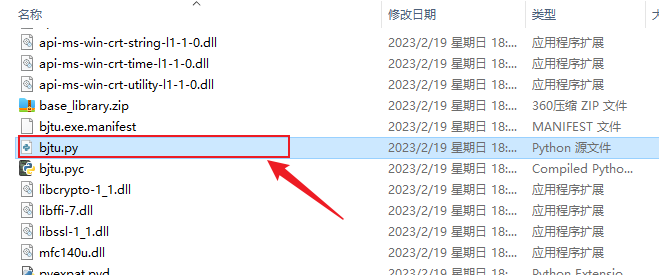
如何将Python打包后的exe还原成.py?
将python打包好的exe解压为py文件,步骤如下:下载pyinstxtractor.py文件下载地址:https://nchc.dl.sourceforge.net/project/pyinstallerextractor/dist/pyinstxtractor.py并将pyinstxtractor.py放到和exe相同的目录文件下打开命令控制台cd 进…...

CJSON简单介绍
json简介 JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式。 易于人阅读和编写。同时也易于机器解析和生成。 它基于JavaScript Programming Language, Standard ECMA-262 3rd Edition - December 1999的一个子集,最新的定义可以参考ECMA-404_2nd_ed…...

算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数
算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数 爬楼梯 (进阶) 70. 爬楼梯 - 力扣(LeetCode) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同…...

Vue:extends继承组件复用性
提到extends继承,最先想到的可能是ES6中的class、TS中的interface、面向对象编程语言中中的类和接口概念等等,但是我们今天的关注点在于:如何在Vue中使用extends继承特性。 目录 Vue:创建Vue实例的方式 构造函数方式࿱…...

ChatGPT 的一些思考
最近 ChatGPT3.5 在全世界范围内掀起了一次 AI 的潮流,ChatGPT1.0/ChatGPT2.0 当时也是比较火爆,但是那个当时感觉还是比较初级的应用,相当于是一个进阶版的微软小冰,给人的感觉是有一点智能,但不多。其实从早期版本开…...
GEE学习笔记 六十九:【GEE之Python版教程三】Python基础编程一
环境配置完成后,那么可以开始正式讲解编程知识。之前我在文章中也讲过,GEE的python版接口它是依赖python语言的。目前很多小伙伴是刚开始学习GEE编程,之前或者没有编程基础,或者是没有学习过python。为了照顾这批小伙伴࿰…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
