mysql的隐式连接和显式连接的区别
隐式连接(Implicit Join)和显式连接(Explicit Join)是 SQL 查询中用于联结多个表的两种不同语法方式。它们的区别主要体现在语法的书写风格和可读性上。
隐式连接:
隐式连接使用逗号 , 将多个表名放在 FROM 子句中,通过条件在 WHERE 子句中连接表。这种连接方式在简单查询时可能很方便,但在复杂查询中会降低可读性,容易出现错误,并且难以维护。
示例:
sql
Copy code
SELECT Orders.OrderID, Customers.CustomerName
FROM Orders, Customers
WHERE Orders.CustomerID = Customers.CustomerID;
显式连接:
显式连接使用 JOIN 关键字将多个表连接起来,更加清晰地表达了表之间的关系。常见的连接类型有 INNER JOIN、LEFT JOIN、RIGHT JOIN 和 FULL JOIN 等。这种连接方式可以更明确地指定连接条件,使查询更易读、易懂,并且在处理复杂情况时更具可维护性。
示例:
sql
Copy code
SELECT Orders.OrderID, Customers.CustomerName
FROM Orders
INNER JOIN Customers ON Orders.CustomerID = Customers.CustomerID;
总之,尽管隐式连接在某些情况下可能更简洁,但显式连接通常更加推荐,因为它提供了更清晰、更具可读性和可维护性的查询方式,尤其在处理复杂的查询场景时更为有利。
Leetcode:https://leetcode.cn/problems/movie-rating/description/
相关文章:

mysql的隐式连接和显式连接的区别
隐式连接(Implicit Join)和显式连接(Explicit Join)是 SQL 查询中用于联结多个表的两种不同语法方式。它们的区别主要体现在语法的书写风格和可读性上。 隐式连接: 隐式连接使用逗号 , 将多个表名放在 FROM 子句中&am…...
vue-element-admin新增view后点击侧边栏加载慢问题
按照官网文档新增view 新增之后点击显示一直在加载中 解决方案:删除script中这段代码...

论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读
论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读 BackgroundIntroducitonProblem StatementMethodology Δ W \Delta W ΔW 的选择 W W W的选择 总结 今天带来的是由微软Edward Hu等人完成并发表在ICLR 2022上的论文《LoRA: Low-Rank Adaptation of Large Lan…...

MySQL数据类型篇
数值类型 类型有符号(SIGNED)取值范围无符号(UNSIGNED)取值范围大小描述TINYINT(-128,127)(0,255)1byte小整数值SMALLINT(-32768,32767)(0,65535)2bytes大整数值INT/INTEGER(-2147483648,2147483647)(0,429…...

Eureka注册中心
全部流程 注册服务中心 添加maven依赖 <!--引用注册中心--> <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId> </dependency> 配置Eureka 因为自…...

代码随想录算法训练营第53天|动态规划part14
8.19周六 1143.最长公共子序列 1035.不相交的线 53. 最大子序和 动态规划 详细布置 1143.最长公共子序列 题目:两个字符串,问最长的公共子序列多长(不连续) 题解: 1、dp[i][j]:长度为[0, i - 1]的字…...
houdini xyzdist primuv 实现按路径走
2. meause distance v 0; add popforce...

Asrock-Z690-PG-Reptide i5-13600kf电脑 Hackintosh 黑苹果引导文件
硬件配置(需要下载请百度搜索:黑果魏叔) 硬件型号驱动情况主板 Asrock Z690 PG Reptide 处理器i5-13600kf RaptorLake (Undervolted)已驱动内存2x16Gb DDR4 3600 ADATA XPG已驱动硬盘1Tb Netac NV7000 NVME M2 (PCI-e 4.0)已驱动显卡Radeon …...
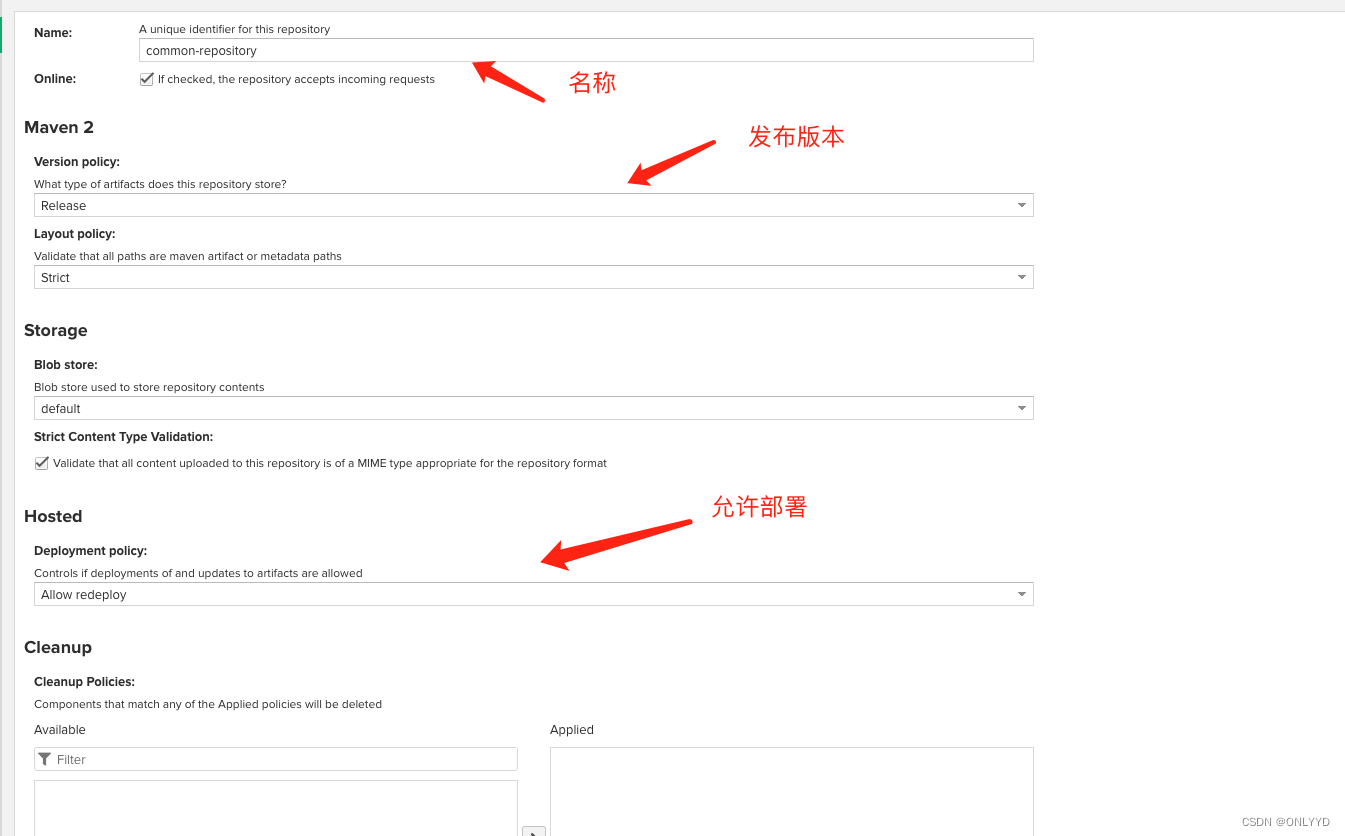
linux 搭建 nexus maven私服
目录 环境: 下载 访问百度网盘链接 官网下载 部署 : 进入目录,创建文件夹,进入文件夹 将安装包放入nexus文件夹,并解压编辑 启动 nexus,并查看状态.编辑 更改 nexus 端口为7020,并重新启动,访问虚拟机7020…...

MySQL中按月统计并逐月累加统计值的几种写法
有时候,我们可能有这样的场景,需要将销量按月统计,并且按月逐月累加。写惯了GROUP BY,按月统计倒是小case,但是逐月累加实现起来,要稍微麻烦一点。下面就整理几种写法,以备不时之需。 本月第一天 -- 本月第一天 SELE…...
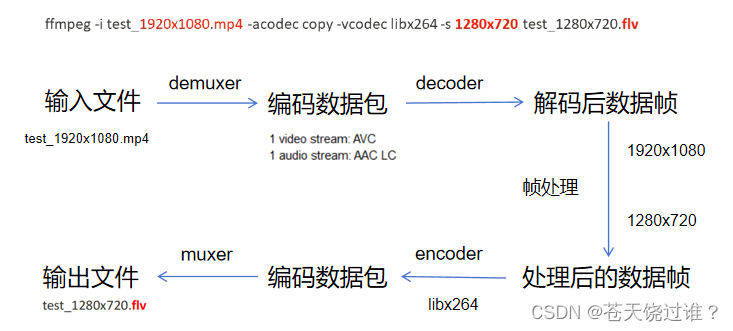
音视频 FFmpeg音视频处理流程
ffmpeg -i test_1920x1080.mp4 -acodec copy -vcodec libx264 -s 1280x720 test_1280x720.flv推荐一个零声学院项目课,个人觉得老师讲得不错,分享给大家: 零声白金学习卡(含基础架构/高性能存储/golang云原生/音视频/Linux内核&am…...

Linux网络编程:多进程 多线程_并发服务器
文章目录: 一:wrap常用函数封装 wrap.h wrap.c server.c client.c 二:多进程process并发服务器 实现思路 server.c服务器 client.c客户端 三:多线程thread并发服务器 实现思路 server.c服务器 client.c客户端 一&am…...
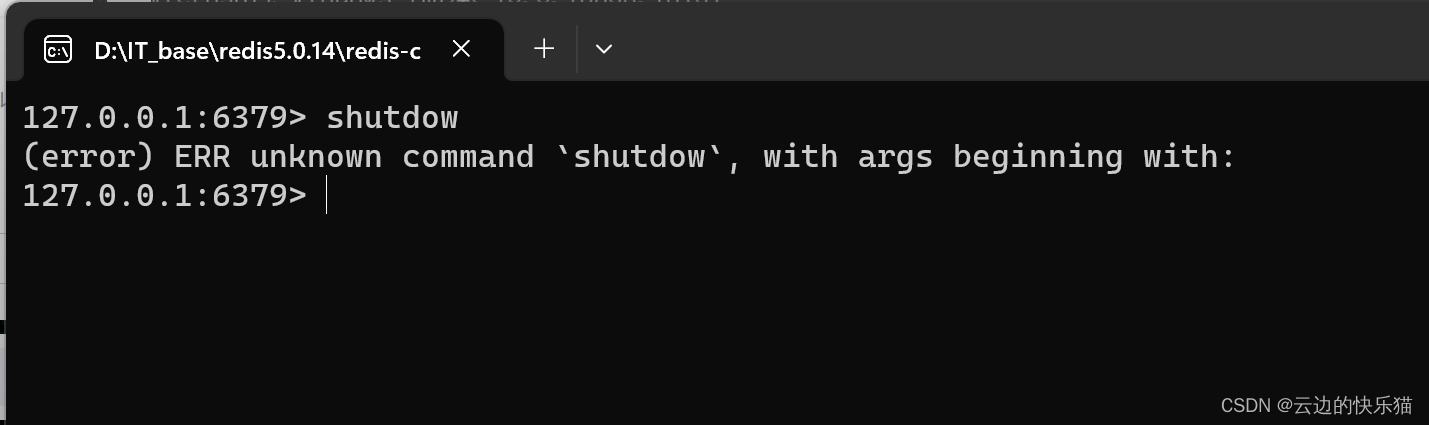
解决:(error) ERR unknown command shutdow,with args beginning with
目录 一、遇到问题 二、出现问题的原因 三、解决办法 一、遇到问题 要解决连接redis闪退的问题,按照许多的方式去进行都没有成功,在尝试使用了以下的命名去尝试时候,发现了这个问题。 二、出现问题的原因 这是一个粗心大意导致的错误&am…...

《TCP IP网络编程》第十八章
第 18 章 多线程服务器端的实现 18.1 理解线程的概念 线程背景: 第 10 章介绍了多进程服务端的实现方法。多进程模型与 select 和 epoll 相比的确有自身的优点,但同时也有问题。如前所述,创建(复制)进程的工作本身会…...

TCP编程流程
目录 1、主机字节序列和网络字节序列 2、套接字地址结构 3、IP地址转换函数 4、TCP协议编程: (1)服务器端: (2)客户端: 1、主机字节序列和网络字节序列 主机字节序列分为大端字节序和小端字节序 大端…...
)
CSDN编程题-每日一练(2023-08-19)
CSDN编程题-每日一练(2023-08-19) 一、题目名称:风险投资二、题目名称:幼稚班作业三、题目名称:韩信点兵一、题目名称:风险投资 时间限制:1000ms内存限制:256M 题目描述: 风险投资是一种感性和理性并存的投资方式,风险投资人一般会对请公允的第三方评估公司对投资对象…...
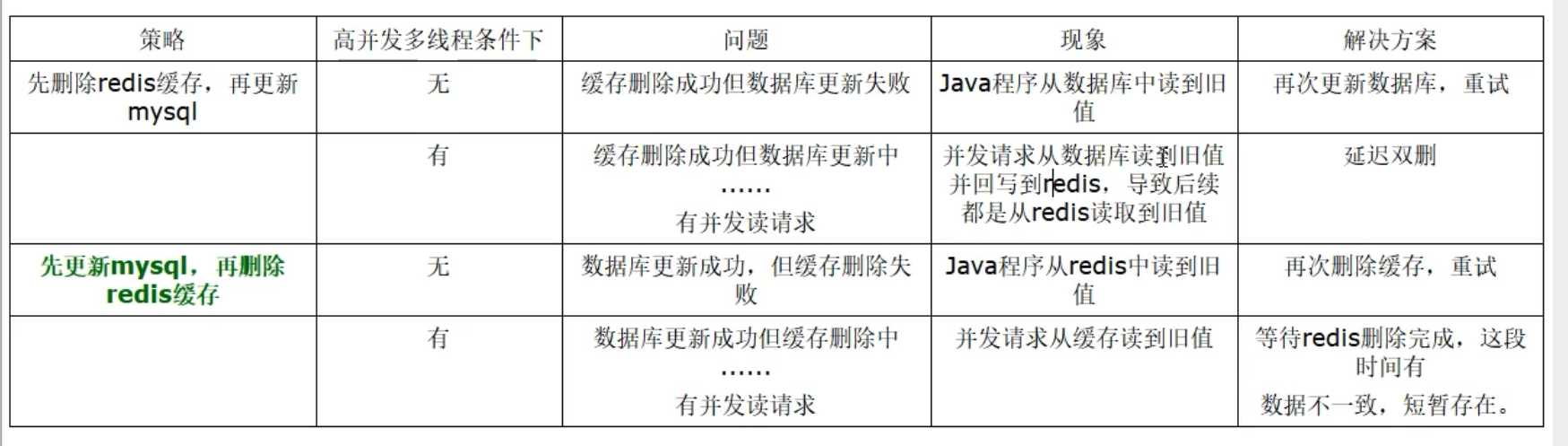
03_缓存双写一致性
03——缓存双写一致性 一、缓存双写一致性 如果redis中有数据,需要和数据库中的值相同如果redis中无数据,数据库中的值要是最新值,且准备回写redis 缓存按照操作来分,可以分为两种: 只读缓存 读写缓存 同步直写操作…...

机器学习之数据集
目录 1、简介 2、可用数据集 3、scikit-learn数据集API 3.1、小数据集 3.2、大数据集 4、数据集使用 ⭐所属专栏:人工智能 文中提到的代码如有需要可以私信我发给你😊 1、简介 当谈论数据集时,通常是指在机器学习和数据分析中使用的一组…...

PyTorch Geometric基本教程
PyG官方文档 # Install torch geometric !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-geometricimport t…...

MAC 命令行启动tomcat的详细介绍
MAC 命令行启动tomcat MAC 命令行启动tomcat的详细介绍 一、修改授权 进入tomcat的bin目录,修改授权 1 2 3 ➜ bin pwd /Users/yp/Documents/workspace/apache-tomcat-7.0.68/bin ➜ bin sudo chmod 755 *.sh sudo为系统超级管理员权限.chmod 改变一个或多个文件的存取模…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
